当前位置： 首页 > news >正文

线性代数再回顾

news 2025/10/19 20:16:52

        最近，在深度学习线性代数，之前大一的时候学过线性代数，但那纯属于是应试用的，考试一考完，啥都忘了，也说出不出个所以然，所以，在B站的MIT的线性代数以及3blue1brown线性代数的本质中去看了一些东西，来记录一下学习过程。

 

 

 

 

 

 

 

 

相关文章：

线性代数再回顾

最近，在深度学习线性代数，之前大一的时候学过线性代数，但那纯属于是应试用的，考试一考完，啥都忘了，也说出不出个所以然，所以，在B站的MIT的线性代数以及3blue1brown线性代数的本质中去…...

编程日记 2023/8/17 22:44:31

（白帽黑客）自学笔记

一、前言： 1.这是一条坚持的道路,三分钟的热情可以放弃往下看了. 2.多练多想,不要离开了教程什么都不会了.最好看完教程自己独立完成技术方面的开发. 3.有时多 google,baidu,我们往往都遇不到好心的大神,谁会无聊天天给你做解答. 4.遇到实在搞不懂的,可以先放放,以…...

编程日记 2023/8/17 22:43:30

基于长短期神经网络的客流量预测，基于长短期神经网络的超短期客流量预测，lstm详细原理

目录 背影 摘要 LSTM的基本定义 LSTM实现的步骤 基于长短期神经网络LSTM的客流量预测 完整代码： 基于长短期神经网络LSTM的公交站客流量预测资源-CSDN文库 https://download.csdn.net/download/abc991835105/88184734 效果图 结果分析 展望 参考论文 背影 碳排放越来越受到重…...

编程日记 2023/8/17 22:42:29

前端文件下载通用方法

zip文件和xlsx文件 import axios from axios import { getToken } from /utils/authconst mimeMap {xlsx: application/vnd.openxmlformats-officedocument.spreadsheetml.sheet,zip: application/zip }const baseUrl process.env.VUE_APP_BASE_API // zip下载 export functi…...

编程日记 2023/8/17 22:41:27

htmlCSS-----案例展示

目录 前言 作品效果 html代码 CSS代码 图片资源 前言 在学习html过程中我们要试着去写写一些案例，通过这些案例让我们更加熟悉代码以及丰富我们的经验，下面是我个人写的一个案例，代码和图片也给出了大家，你们可以参考参考。…...

编程日记 2023/8/17 22:40:25

Android进阶之路 - 去除EditText内边距

正如题名，在Android中的EditText是自带内边距的，常规而言设置背景为null即可，但是因为使用了并不熟悉的声明式框架，本是几分钟解决的事儿，却花费了小半天~ 其实这只是一个很简单的小需求，不想却遇到了一些小…...

编程日记 2023/8/17 22:39:24

ModStartCMS v7.0.0 多语言开发优化，多个常用组件升级

ModStart 是一个基于 Laravel 模块化极速开发框架。模块市场拥有丰富的功能应用，支持后台一键快速安装，让开发者能快的实现业务功能开发。 系统完全开源，基于 Apache 2.0 开源协议，免费且不限制商业使用。 功能特性 丰富的模块市…...

编程日记 2023/8/17 22:38:23

一百五十八、Kettle——Kettle各版本及其相关安装包分享（网盘链接，不需积分、不需验证码） 持续更新、持续分享

一、目的 最近因为kettle9.3的shim问题看了好多博客，都没有网盘分享。后来有一位博主分享了kettle9.2的shim安装包，已经很感谢他，但是是博客分享，下载还需要搞验证码下载码之类的。 kettle9.2的shim安装包下载好后，一…...

编程日记 2023/8/17 22:37:21

【通俗易懂】如何使用GitHub上传文件，如何用git在github上传文件

目录 创建 GitHub 仓库 使用 Git 进行操作 步骤 1：初始化本地仓库 步骤 2：切换默认分支 步骤 3：连接到远程仓库 步骤 4：获取远程更改 步骤 5：添加文件到暂存区 步骤 6：提交更改 步骤 7&#xff1a…...

编程日记 2023/8/17 22:36:17

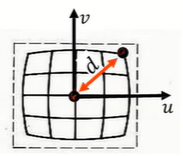
计算机视觉之三维重建(二)(摄像机标定)

标定示意图 标定目标 P ′ M P w K [ R T ] P w P^{}MP_wK[R \space T]P_w P′MPw​K[R T]Pw​ 其中 K K K为内参数， [ R T ] [R \space T] [R T]为外参数。该式子需要使用至少六对内外点对进行求解内外参数（11个未知参数）。 其中 R 3 3 …...

编程日记 2023/8/17 22:35:16

PHP面向对象面试题

1、简述面对对象六大设计原则 ？ 面向对象六大设计原则是一组指导软件设计的原则，它们有助于提高代码的可维护性、可扩展性和可重用性。这些原则是： 单一职责原则（Single Responsibility Principle，SRP）&a…...

编程日记 2023/8/17 22:34:15

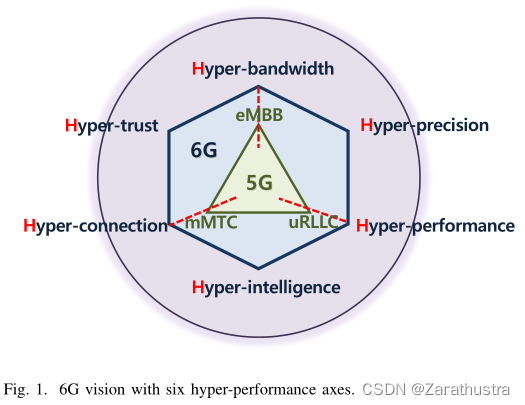
6G 特点及表现

6G R&D Vision: Requirements and Candidate Technologies 5G已经提出来了大移动带宽，低时延和大规模机器互联，在这个基础上，6G加上了高可靠性，高定位精度和高智能化。 6G的主要候选技术，包括(子) THz 通信&#x…...

编程日记 2023/8/17 22:33:13

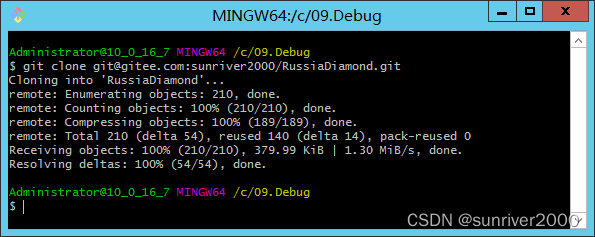
【Git】（一）基本操作

读完本文后，您会了解： 1、如何在本地配置GIT环境？ 2、环境配置成功后，如何从远端下载一个已有仓库到本地? 1. 配置全局用户名、邮箱 git config --global user.name "username" git config --global user.email &q…...

编程日记 2023/8/17 22:32:11

Github下载任意版本的VsCode

下载历史版本VsCode(zip) 下载链接由三部分组成： 固定部分commit idVSCode-win32-x64-版本号.zip 固定部分： https://vscode.cdn.azure.cn/stable/ Commit id： 打开 vscode的GitHub：[https://github.com/microsoft/vscode/r…...

编程日记 2023/8/17 22:31:09

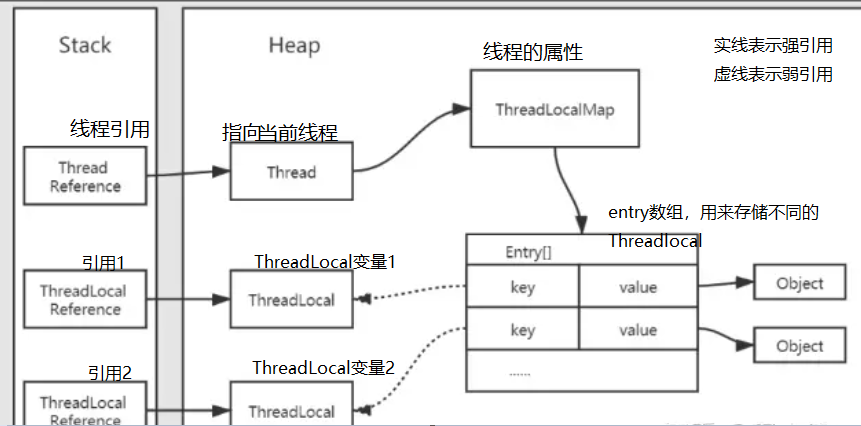
ThreadLocal（超详细介绍！！）

关于ThreadLocal，可能很多同学在学习Java的并发编程部分时，都有所耳闻，但是如果要仔细问ThreadLocal是个啥，我们可能也说不清楚，所以这篇博客旨在帮助大家了解ThreadLocal到底是个啥？ 1.ThreadLocal是什么&…...

编程日记 2023/8/17 22:30:08

stable diffusion安装包和超火使用文档，数字人制作网址

一：文生图、图生图 1：stable diffusion：对喜欢二次元、美女小姐姐、大眼萌妹的人及其友好哈哈(o^^o) 1）：秋叶大神安装包和模型包： 链接：https://pan.baidu.com/s/11_kguofh76gwhTBPUipepw 提…...

编程日记 2023/8/17 22:29:07

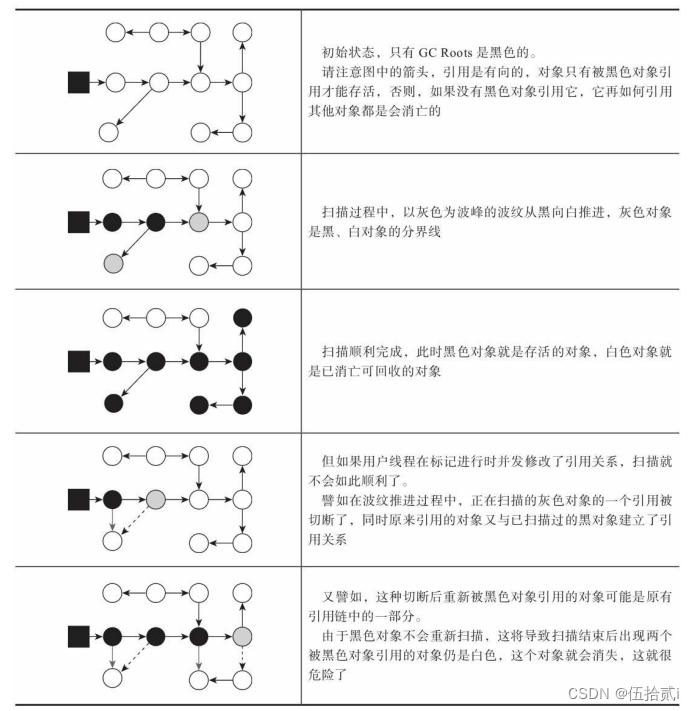
JVM——HotSpot的算法细节实现

一、根节点枚举 固定可作为GC Roots的节点主要在全局性的引用（如常量或类静态属性）与执行上下文（如栈帧中的本地变量表）中，尽管目标明确，但查找要做到高效很难。现在java应用越来越庞大，光方法区…...

编程日记 2023/8/17 22:28:06

高等数学教材重难点题型总结（三）微分中值定理和导数的应用

第三章，微分中值定理的证明题等，非常重要，需要牢牢掌握 1.证明中值定理对某函数在给定区间上的正确性 2.与中值定理有关的证明题 3.微分中值定理应用于求证不等式 4.洛必达法则求极限 5.洛必达的经典错误反例 6.按某项实现多项式幂展开 7.求带…...

编程日记 2023/8/17 22:27:05

神经网络基础-神经网络补充概念-39-梯度消失与梯度爆炸

简介 梯度消失和梯度爆炸是在深度神经网络中训练过程中可能出现的问题，导致模型难以训练或无法收敛。这些问题与反向传播算法中的梯度计算有关。 概念 梯度消失（Gradient Vanishing）：在深层神经网络中，特别是具有很…...

编程日记 2023/8/17 22:25:01

P12-Retentive NetWork-RetNet挑战Transformer

论文地址:https://arxiv.org/abs/2307.08621 目录 Abstract 一.Introduction 二.Retentive Networks 2.1Retention 2.2Gated Multi-Scale Retention 2.3Overall Architecture of Retention Networks 2.4Relation to and Differences from Previous Methods 三.Experime…...

编程日记 2023/8/17 22:23:58

vscode里如何用git

打开vs终端执行如下： 1 初始化 Git 仓库（如果尚未初始化） git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

编程新知 2025/8/24 20:45:38

云原生核心技术 (7/12): K8s 核心概念白话解读(上)：Pod 和 Deployment 究竟是什么？

大家好，欢迎来到《云原生核心技术》系列的第七篇！ 在上一篇，我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在，我们就像一个拥有了一块崭新数字土地的农场主，是时…...

编程新知 2025/9/6 5:44:49

＜6＞-MySQL表的增删查改

目录 一，create（创建表） 二，retrieve（查询表） 1，select列 2，where条件 三，update（更新表） 四，delete（删除表&#xf…...

编程新知 2025/8/6 22:35:04

通过Wrangler CLI在worker中创建数据库和表

官方使用文档：Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后，会在本地和远程创建数据库： npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库： 现在，您的Cloudfla…...

编程新知 2025/10/18 7:02:36

AtCoder 第409​场初级竞赛 A~E题解

A Conflict 【题目链接】 原题链接：A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串，只有在同时为 o 时输出 Yes 并结束程序，否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

编程新知 2025/7/23 9:09:08

c++ 面试题(1)-----深度优先搜索（DFS）实现

操作系统：ubuntu22.04 IDE:Visual Studio Code 编程语言：C11 题目描述 地上有一个 m 行 n 列的方格，从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子，但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

编程新知 2025/10/14 13:55:53

【算法训练营Day07】字符串part1

文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接&#xff1a;344. 反转字符串 双指针法&#xff0c;两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

编程新知 2025/8/27 14:38:58

根据万维钢·精英日课6的内容，使用AI（2025）可以参考以下方法：

根据万维钢精英日课6的内容&#xff0c;使用AI&#xff08;2025&#xff09;可以参考以下方法&#xff1a; 四个洞见 模型已经比人聪明&#xff1a;以ChatGPT o3为代表的AI非常强大&#xff0c;能运用高级理论解释道理、引用最新学术论文&#xff0c;生成对顶尖科学家都有用的…...

编程新知 2025/10/15 12:45:18

Rapidio门铃消息FIFO溢出机制

关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系&#xff0c;以下是深入解析&#xff1a; 门铃FIFO溢出的本质 在RapidIO系统中&#xff0c;门铃消息FIFO是硬件控制器内部的缓冲区&#xff0c;用于临时存储接收到的门铃消息&#xff08;Doorbell Message&#xff09;。…...

编程新知 2025/9/12 21:09:32

腾讯云V3签名

想要接入腾讯云的Api&#xff0c;必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口&#xff0c;但总是卡在签名这一步&#xff0c;最后放弃选择SDK&#xff0c;这次终于自己代码实现。 可能腾讯云翻新了接口文档&#xff0c;现在阅读起来&#xff0c;清晰了很多&…...

编程新知 2025/10/19 18:56:12