数学建模之“聚类分析”原理详解
一、聚类分析的概念
1、聚类分析(又称群分析)是研究样品(或指标)分类问题的一种多元统计法。
2、主要方法:系统聚类法、有序样品聚类法、动态聚类法、模糊聚类法、图论聚类法、聚类预报法等。这里主要介绍系统聚类法。根据事物本身的特性研究个体分类的方法,原则是同一类中的个体有较大的相似性,不同类间的个体差异很大。根据分类对象的不同,分为样品(观测量)聚类和变量聚类两种。样品聚类是对观测量(Case)进行聚类(不同的目的选用不同的指标作为分类的依据);变量聚类是找出彼此独立且有代表性的自变量,而又不丢失大部分信息。
3、按照远近程度来聚类需要明确两个概念:一个是点和点之间的距离,另一个是类和类之间的距离。点间距离有很多定义的方式。最简单的是欧氏距离,还有其他的距离,比如相似度等。两点相似度越大,就相当于距离越短。
4、由一个点组成的类是最基本的类,如果每一类都由一个点组成,那么点间距离就是类间距离。但如果某一类包含不止一个点,那么就要确定类间距离。比如两类之间最近点之间的距离可以作为这两类之间的距离,也可以用两类中最远点之间的距离作为这两类之间的距离;当然也可以用各类的中心之间的距离作为类间距离。在计算时,各种点间距离和类间距离的选择可以通过统计软件的选项来实现。不同选择的结果会不同。
二、Q型聚类常用的距离
记第i个样品Xi与第j 个样品Xj之间距离d(Xi, Xj)≜dij,它满足以下条件:

通过计算可得一对称矩阵D=(dij)n×n, dii=0。dij越小,说明Xi与Xj越接近。可以用作这里的距离有很多,常用的距离有以下三种:
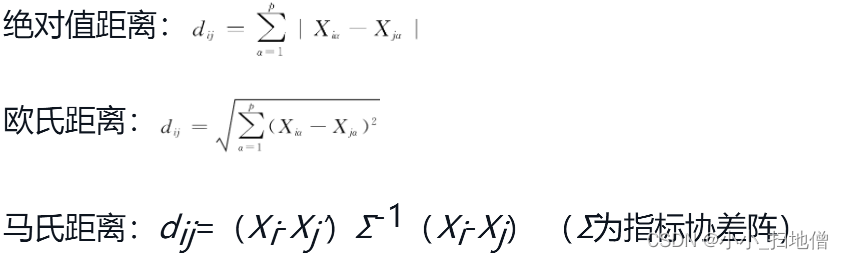
三、R型聚类分析常用的相似系数
如果cij满足以下三个条件,则称其为变量Xi与Xj的相似系数:
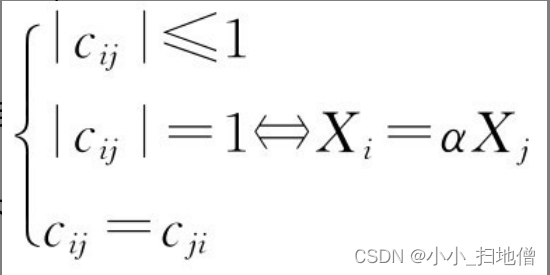
|cij|越接近于1,则Xi与Xj的关系越密切。
常用的相似系数有以下两种:
夹角余弦(向量内积):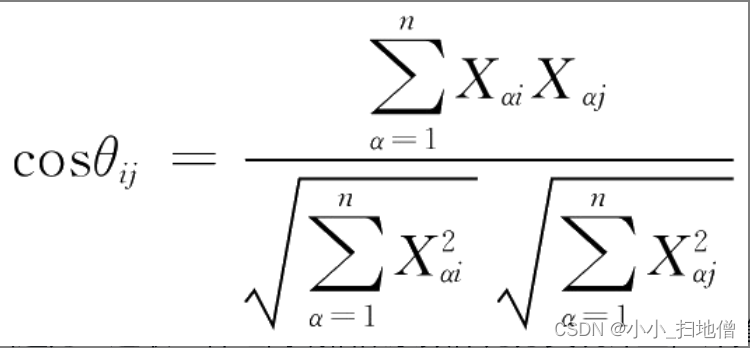
相关系数:

聚类过程可以描述为:选取一种距离或相似系数作为分类统计量;计算任何两个样品Xi与Xj之间的距离或相似系数排成一个距离矩阵或相似系数矩阵;规定一种并类规则(距离:越小越接近,相似系数:越大越接近)。
类与类之间距离定义法不同,产生了不同的系统聚类法:最短距离法、最长距离法、中间距离法、重心法、类平均法、可变类平均法、可变法、离差平方和法。
他们的定义如下:
● 最短距离法:类之间距离为两类最近样品之间的距离。
● 最长距离法:类之间距离为两类最远样本之间的距离。
● 中间距离法:如果类与类之间的距离既不采用两者之间的最短距离也不采用两者之间的最长距离,而是采用两者之间的中间距离。
● 重心法:从物理观点看,类与类之间的距离可以用重心(该类样品的均值)之间的距离来代表。
● 类平均法:类重心法未能充分利用各样品的信息,为此可将两类之间距离平方定义为这两类元素两两元间的距离平方平均。
四、相关概念和原理补充
(一)、什么是聚类分析
聚类(Clustering):
1、聚类是一个将数据集划分为若干组( class) 或类( cluster)的过程, 并使得同一个组内的数据对象具有较高的相似度;而不同组中的数据对象是不相似的。
2、相似或不相似是基于数据描述属性的取值来确定的, 通常利用各数据对象间的距离来进行表示。
3、聚类分析尤其适合用来探讨样本间的相互关联关系从而对一个样本结构做一个初步的评价。
(二)、举例
1、示例一
表中给出9个顾客的购买信息, 包括购买的商品的数量及价格, 根据此两个特征量, 将顾客聚类成3类( 购买大量的高价产品; 购买少量的高价产品; 购买少量的低价产品) 。

2、示例二
聚类是一个非常困难的事情, 因为在一个n维样本空间中, 数据可以以不同的形状和大小揭示类。
如在二维欧几里得空间中, 上面数据可以分类三个类也可以分为四个类, 类的数量的任意性是聚类过程中的主要问题。

(三)、聚类与分类的区别:
聚类是一 种无( 教师) 监督的学习方法。 与分类不同, 其不依赖于事先确定的数据类别, 以及标有数据类别的学习训练样本集合。 因此, 聚类是观察式学习, 而不是示例式学习。
(四)、什么是好的聚类
1、一个好的聚类方法将产生以下的高聚类:
最大化类内的相似性;
最小化类间的相似性。
2、聚类结果的质量依靠所使用度量的相似性和它的执行。
3、聚类方法的质量也可以用它发现一些或所有隐含模式的能力来度量。
(五)、聚类分析的种类
聚类分析有两种: 一种是对样品的分类, 称为Q型, 另一种是对变量( 指标) 的分类, 称为R型。
R型聚类分析的主要作用:
(1) 不但可以了解个别变量之间的亲疏程度, 而且可以了解各个变量组
合之间的亲疏程度。
(2) 根据变量的分类结果以及它们之间的关系, 可以选择主要变量进行Q
型聚类分析或回归分析。 (R2为选择标准)
Q型聚类分析的主要作用:
(1) 可以综合利用多个变量的信息对样本进行分析。
(2) 分类结果直观, 聚类谱系图清楚地表现数值分类结果。
(3) 聚类分析所得到的结果比传统分类方法更细致、 全面、 合理。
(六)、样品间的相似度量—距离

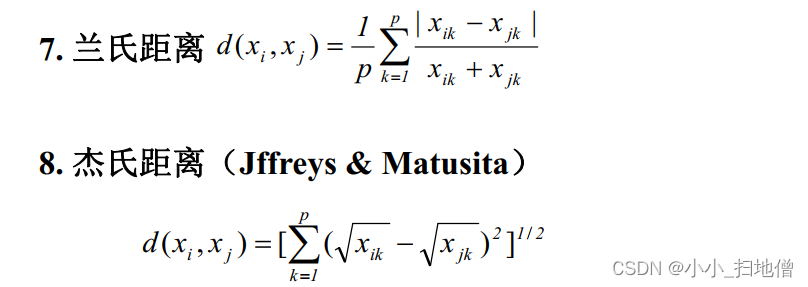
(七)、典型例题
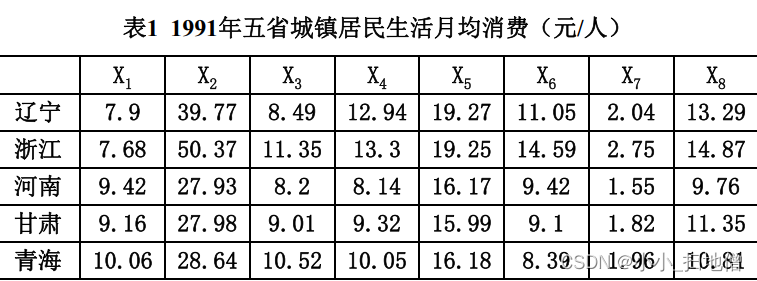
例1.为了研究辽宁、 浙江、 河南、 甘肃、 青海5省1991年城镇居民生活消费规律, 需要利用调查资料对五个省进行分类,指标变量共8个, 意义如下: x1:人均粮食支出, x2:人均副食支出;x3:人均烟酒茶支出, x4:人均其他副食支出,x5:人均衣着商品支出,x6:人均日用品支出, x7:人均燃料支出, x8人均非商品支出


(八)、变量间的相似度量——相似系数
当对p个指标变量进行聚类时, 用相似系数来衡量变量之间的相似程度( 关联度) , 若用 表示变量之间的相似系数, 则应满足:
1、① 夹角余弦。两变量的夹角余弦定义为:

2、② 相关系数。两变量的相关系数定义为:
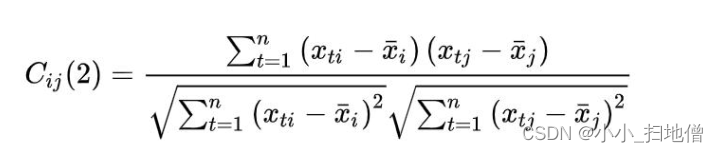

(九)、类间距离
前面, 我们介绍了两个向量之间的距离, 下面我们介绍两个类别之间的距离:
设dij表示两个样品xi,xj之间的距离, Gp,Gq分别表示两个类别, 各自含有np,nq个样品.
(1)、最短距离,即用两类中样品之间的距离最短者作为两类间距离
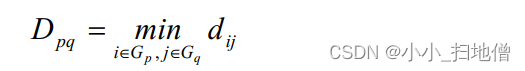
(2)、最长距离,即用两类中样品之间的距离最长者作为两类间距离

(3)、类平均距离,即用两类中所有两两样品之间距离的平均作为两类间距离
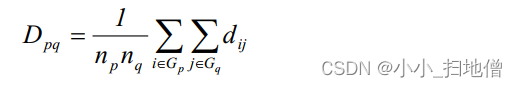
(4)、重心距离
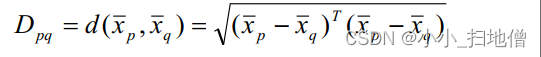

(5)、离差平方和距离( ward)

显然, 离差平方和距离与重心距离的平方成正比。
(十)、谱系聚类法的步骤
1. 选择样本间距离的定义及类间距离的定义;
2. 计算n个样本两两之间的距离, 得到距离矩阵
3. 构造个类, 每类只含有一个样本;
4. 合并符合类间距离定义要求的两类为一个新类;
5. 计算新类与当前各类的距离。 若类的个数为1, 则转到步骤6, 否则回到步骤4;
6.画出聚类图;
7.决定类的个数和类。
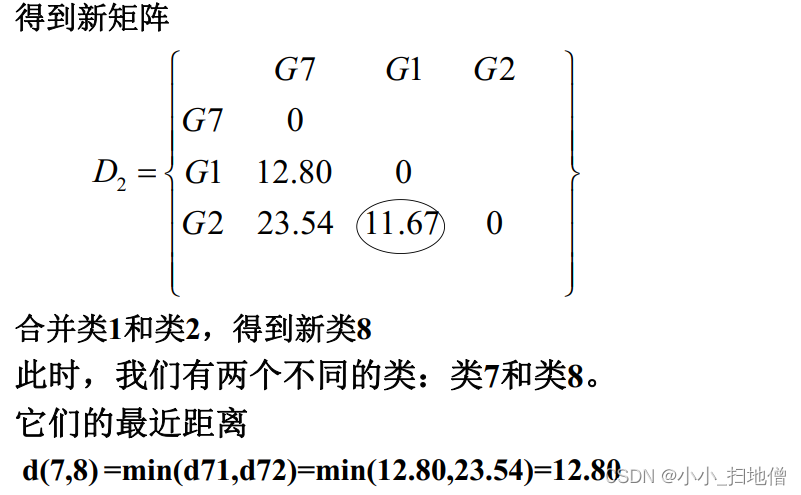
(1) n个样品开始作为n个类, 计算两两之间的距离或相似系数, 得到实对称矩阵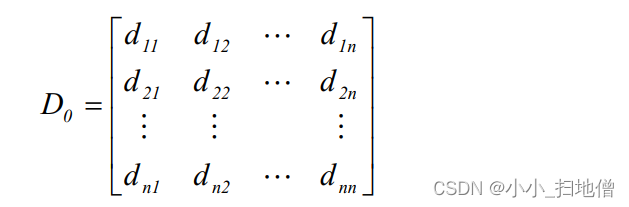
( 2) 从D0的非主对角线上找最小( 距离) 或最大元素( 相似系数) , 设该元素是Dpq, 则将Gp,Gq合并成一个新类Gr=( Gp,Gq) , 在D0中去掉Gp,Gq所在的两行、 两列, 并加上新
类与其余各类之间的距离(或相似系数), 得到n-1阶矩阵D1。
(3) 从D1出发重复步骤( 2) 的做法得到D2, 再由D2出发重复上述步骤, 直到所有样品聚为一个大类为止。
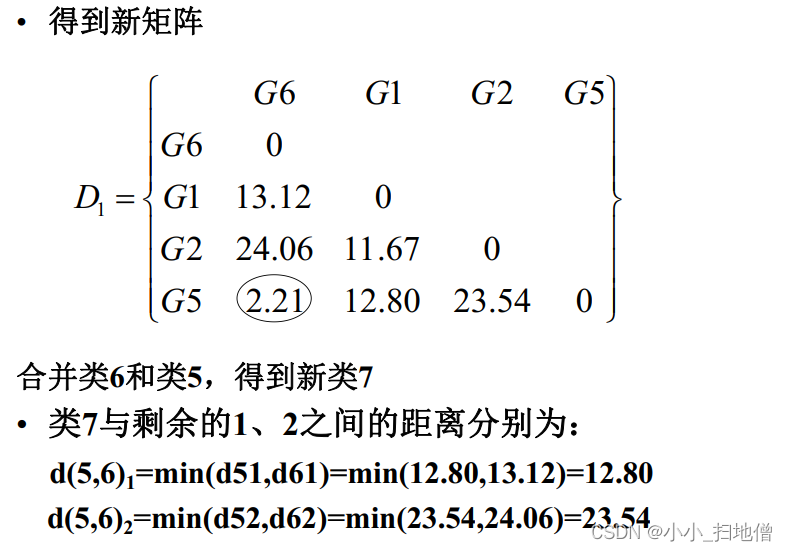
(4) 在合并过程中要记下合并样品的编号及两类合并时的水平, 并绘制聚类谱系图。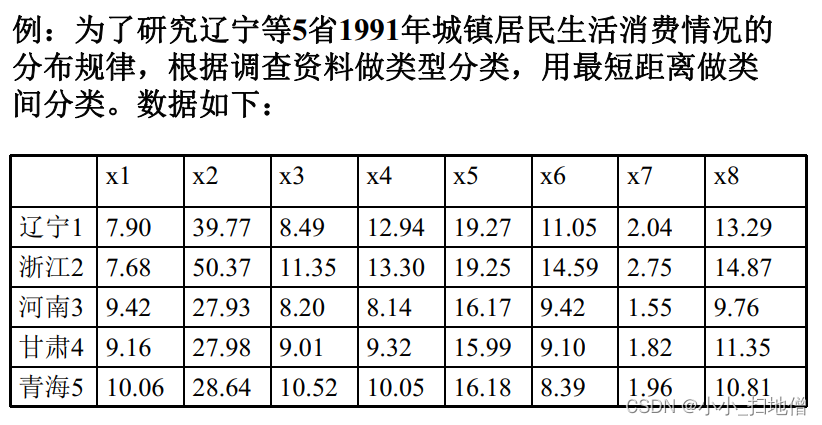


(十一)、 谱系聚类的MATLAB实现:
(1) 输入数据矩阵, 注意行与列的实际意义;
(2) 计算各样品之间的距离( 行? 列? )
欧氏距离: d=pdist(A)% 注意计算A中各行之间的距离;
绝对距离: d= pdist(A,'cityblock');
明氏距离: d=pdist(A,'minkowski',r);% r要填上具体的实数
方差加权距离: d= pdist(A,'seuclid');
马氏距离: d= pdist(A,'mahal');
注意: 以上命令输出的结果是一个行向量, 如果要得到距离矩阵, 可以用命令:
D= squareform(d),
若得到三角阵, 可以用命令:
D= tril(squareform(d1)) %下三角函数
(3) 选择不同的类间距离进行聚类
| 最短距离: z1= linkage(d) 算出的距离行向量 | % 此处及以下的d都( 2) 中 |
最长距离: z2= linkage(d,'complete')
中间距离: z3= linkage(d,'centroid')
重心距离: z4= linkage(d,'average')
离差平方和: z5= linkage(d,'ward')
注意: 此时输出的结果是一个n-1行3列的矩阵, 每一行表示在某水平上合并为一类的序号;
(4) 作出谱系聚类图
H=dendrogram(z,d) % 注意若样本少于30, 可以省去d,否则必须填写.
(5) 根据分类数目, 输出聚类结果
T=cluster(z,k) % 注意k是分类数目, z是( 3) 中的结果
Find(T==k0) % 找出属于第k0类的样品编号
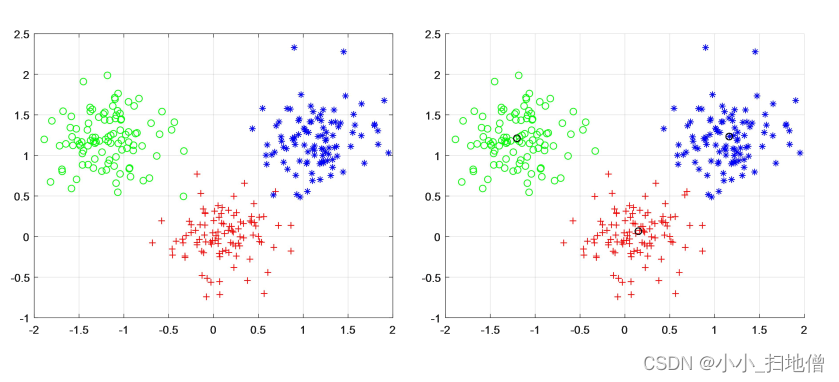
(十二)、K-平均聚类算法
1、K-平均(k-means) 算法以k为参数, 把n个对象分为k个簇, 以使簇内对象具有较高的相似度, 而簇间的相似度较低。
2、相似度的计算根据一个簇中对象的平均值(被看作簇的重心) 来进行。






以上就是我对数学建模“聚类分析”算法的总结和分享。希望我的分享对你有所启发!愿我们携手共进,逐梦不止!最后,敬请关注,持续更新中~~~
相关文章:

数学建模之“聚类分析”原理详解
一、聚类分析的概念 1、聚类分析(又称群分析)是研究样品(或指标)分类问题的一种多元统计法。 2、主要方法:系统聚类法、有序样品聚类法、动态聚类法、模糊聚类法、图论聚类法、聚类预报法等。这里主要介绍系统聚类法…...

【面试问题】当前系统查询接口需要去另外2个系统库中实时查询返回结果拼接优化思路
文章目录 场景描述优化思路分享资源 场景描述 接口需要从系统1查询数据,查出的每条数据需要从另一个系统2中再去查询某些字段, 比如:从系统1中查出100条数据,每条数据需要去系统2中再去查询出行数据,可能系统1一条数…...
Scada和lloT有什么区别?
人们经常混淆SCADA(监督控制和数据采集)和IIoT(工业物联网)。虽然SCADA系统已经存在多年,但IIoT是一种相对较新的技术,由于其能够收集和分析来自各种设备的大量数据而越来越受欢迎。SCADA和IIoT都用于提高工…...
)
Conda(Python管理工具)
1.简介 Conda是一个开源的包管理器和环境管理器,主要用于管理Python,但也可以用于其他语言。它主要用于安装、管理和更新软件包及其依赖项,以及创建、保存、加载和切换不同的开发环境。Conda可以在Windows、MacOS和Linux系统上使用ÿ…...
嵌套列表,Xpath路径表达式,XML增删查改,Implicit,Operator,Xml序列化,浅拷贝与深拷贝)
(14)嵌套列表,Xpath路径表达式,XML增删查改,Implicit,Operator,Xml序列化,浅拷贝与深拷贝
一、作业问题 1、问:listbox1.items[i]返回的object是指的字符串吗? 答:items是真正的对象集合,在Add时加的是Person对象p,则里面的item就是Person对象p。 但是,在listbox1显…...
软考笔记 信息管理师 高级
文章目录 介绍考试内容与时间教材 预习课程一些例子课本结构考试内容 1 信息与信息化1.1 信息与信息化1.1.1 信息1.1.2 信息系统1.1.3 信息化 1.2 现代化基础设施1.2.1 新型基础建设1.2.2 工业互联网1.2.3 车联网: 1.3 现代化创新发展1.3.1 农业农村现代化1.3.2 两化…...

124、SpringMVC处理一个请求的流程是怎样的?
SpringMVC处理一个请求的流程是怎样的? 一、处理流程二、流程图三、额外扩展(可不看)一、处理流程 Tomcat接收到一个请求后,会交给DispatcherServlet进行处理DispatcherServlet会根据请求的path找到对应的HandlerHandler就是一个加了@RequestMapping的方法,然后就利用反射…...
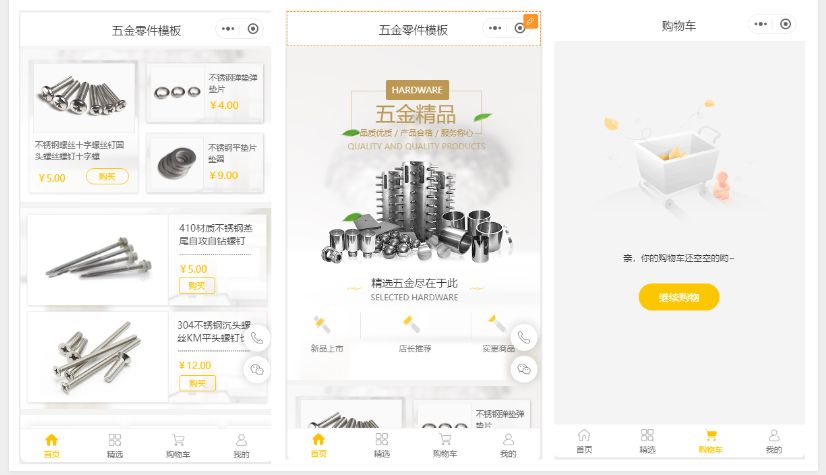
低成本高收益,五金店小程序的秘密武器
如今,随着移动互联网的快速发展,小程序成为了许多企业进行线上业务拓展的重要方式之一。对于那些不懂代码的人来说,制作一个小程序可能会让人觉得困难重重。但是,现在,借助乔拓云平台,不懂代码的人也能轻松…...

C语言宏定义详解
文章目录 宏定义无参宏定义带参宏定义固定参数宏可变参数宏 多语句宏处理连接符条件判断常见预定义宏 宏在C语言中是一段有名称的代码片段(使用#define定义),在预处理阶段会把程序中的宏名替换为对应的代码片段,然后才进入编译阶段…...

SwiftUI 动画进阶:实现行星绕圆周轨道运动
0. 概览 SwiftUI 动画对于优秀 App 可以说是布帛菽粟。利用美妙的动画我们不仅可以活跃界面元素,更可以单独打造出一整套生动有机的世界,激活无限可能。 如上图所示,我们用动画粗略实现了一个小太阳系:8大行星围绕太阳旋转,而卫星们围绕各个行星旋转。 在本篇博文中,您将…...

物理试题-空气净化器
详细解释...
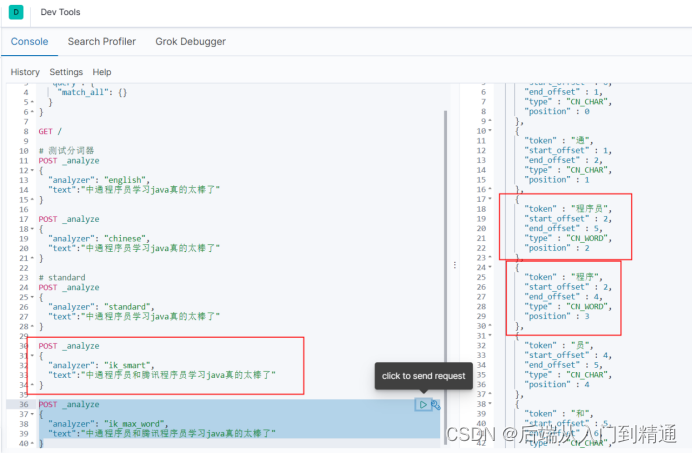
Es、kibana安装教程-ES(二)
上篇文章介绍了ES负责数据存储,计算和搜索,他与传统数据库不同,是基于倒排索引来解决问题的。Kibana是es可视化工具。 分布式搜索ElasticSearch-ES(一) 一、ElasticSearch安装 官网下载地址:https://www…...

leetcode 917.仅仅反转字母
⭐️ 题目描述 🌟 leetcode链接:仅仅反转字母 ps: 这道题思路很简单,只需要一个下标在前一个下标在后,分别找是字母的字符,找到之后交换即可。 代码: class Solution { public:bool isAlpha …...
有没有推荐的golang的练手项目?
前言 下面是github上的golang项目,适合练手,可以自己选择一些项目去练习,整理不易,希望能多多点赞收藏一下!废话少说,我们直接进入正题>>> 先推荐几个教程性质的项目(用于新手学习、巩…...
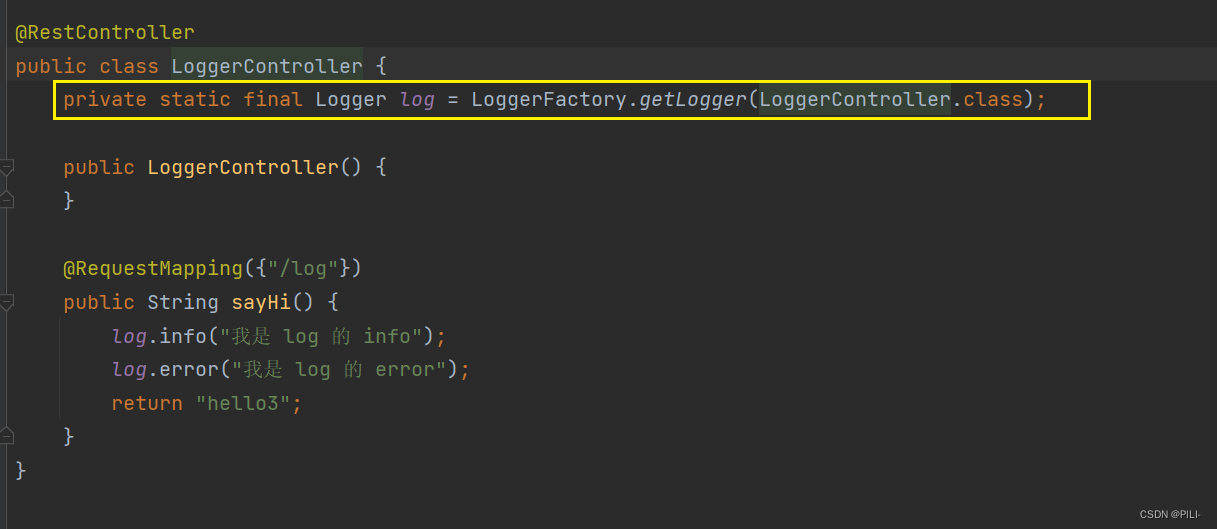
springBoot的日志文件
日志是程序的重要组成部分,主要可以用来定位和排查问题。除此之外,还可以用来: 1. 记录用户的登录日志,方便分析用户是正常登录还是恶意破解; 2. 记录系统的操作日志,方便数据恢复和定位操作人;…...
Linux学习之iptables的nat表
iptables -t nat 命令 规则链 规则是格式命令。 PREROUTING一般用于内网,用于目的地址转换。 POSTROUTING一般用于外网,用于源地址转换。 iptables -t nat -A PREROUTING -i eth0 -d 114.115.116.117 -p tcp --dport 80 -j DNAT --to-destination 10.0.0…...
【数据结构】 ArrayList简介与实战
文章目录 什么是ArrayListArrayList相关说明 ArrayList使用ArrayList的构造无参构造指定顺序表初始容量利用其他 Collection 构建 ArrayListArrayList常见操作获取list有效元素个数获取和设置index位置上的元素在list的index位置插入指定元素删除指定元素删除list中index位置上…...

您的网站不应该只提供一套通用 API
后端应该提供两套 API,一套是外部使用的通用 API,服务特定的数据,另一套是自家使用的应用 API,服务特定的页面。 在当今的web开发中,构建一个提供JSON服务的后端和一个渲染应用程序的前端是很流行的。我不太喜欢&…...

vue tree禁用和多选变为单选
禁用的话和后台协调一下,参数中多返回一个disabled 多选变单选 在tree结构中加入一个方法 <el-treeaccordion:data"deptOptions":props"defaultProps"show-checkbox:expand-on-click-node"false":filter-node-method"filte…...

ES6新特性。对象、数组新增方法
ES6新特性 ES6(ECMAScript 2015)是 JavaScript 的一个重要版本,引入了许多新的语法和功能,增强了语言的表达能力和开发体验。以下是 ES6 中一些重要的新特性的全面总结: let 和 const 声明: let 和 const …...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
