面试之快速学习STL-set
set
- 和 map、multimap 容器不同,使用 set 容器存储的各个键值对,要求键 key 和值 value 必须相等
- 使用 set 容器存储的各个元素的值必须各不相同
- 从语法上讲 set 容器并没有强制对存储元素的类型做 const 修饰, 即 set 容器中存储的元素的值是可以修改的。但是,C++ 标准为了防止用户修改容器中元素的值,对所有可能会实现此操作的行为做了限制,使得在正常情况下,用户是无法做到修改 set 容器中元素的值的。
- 对于初学者来说,切勿尝试直接修改 set 容器中已存储元素的值,这很有可能破坏 set 容器中元素的有序性,最正确的修改 set 容器中元素值的做法是:先删除该元素,然后再添加一个修改后的元素。
模版
set 容器的类模板定义如下:
template < class T, // 键 key 和值 value 的类型class Compare = less<T>, // 指定 set 容器内部的排序规则class Alloc = allocator<T> // 指定分配器对象的类型> class set;
初始化
std::set<std::string> myset{"http://c.biancheng.net/java/","http://c.biancheng.net/stl/","http://c.biancheng.net/python/"};std::set<std::string> copyset(myset);
迭代器
- 成员方法返回的迭代器,无论是 const 类型还是非 const 类型,都不能用于修改 set 容器中的值。
😂其他真的没啥好讲的和map multimap一样
相关文章:

面试之快速学习STL-set
set 和 map、multimap 容器不同,使用 set 容器存储的各个键值对,要求键 key 和值 value 必须相等使用 set 容器存储的各个元素的值必须各不相同从语法上讲 set 容器并没有强制对存储元素的类型做 const 修饰, 即 set 容器中存储的元素的值是可以修改的。…...

leetcode 1614.括号的最大嵌套深度
⭐️ 题目描述 🌟leetcode链接:括号的最大嵌套深度 ps: 使用数据结构栈来存储 ( 在使用 maxDepth 变量记录栈顶 top 的最大值,当遇到 ) 时删除栈顶元素。举个例子 (1)((2))(((3))),当遇到第一个 ( 时 top 1ÿ…...
Ajax 笔记(四)—— Ajax 进阶
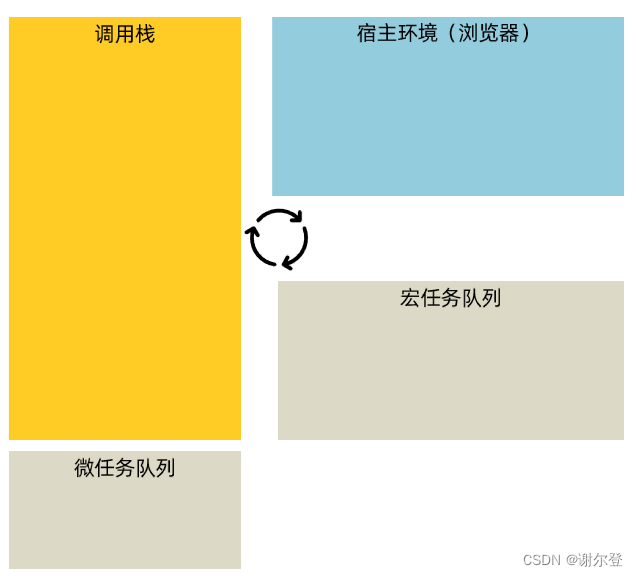
笔记目录 4. Ajax 进阶4.1 同步代码和异步代码4.2 回调函数地狱4.2.1 解决方法一:Promise 链式调用4.2.2 解决方法二:async 函数和 await 4.3 Promise.all 静态方法4.4 事件循环4.4.1 事件循环4.4.2 宏任务与微任务 4.5 案例4.5.1 案例一-商品分类4.5.2 …...
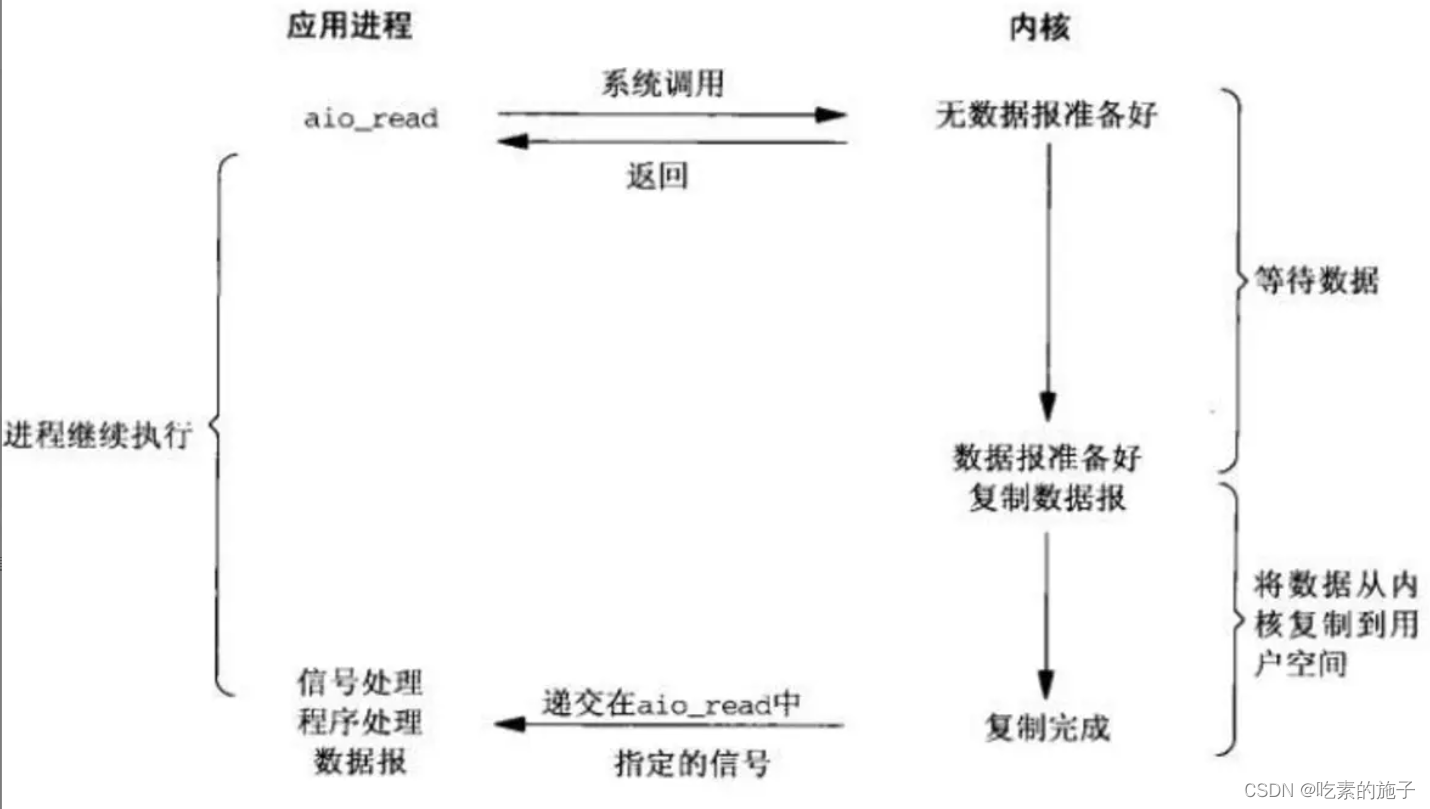
Linux 5种网络IO模型
Linux IO模型 网络IO的本质是socket的读取,socket在linux系统被抽象为流,IO可以理解为对流的操作。刚才说了,对于一次IO访问(以read举例),数据会先被拷贝到操作系统内核的缓冲区中,然后才会从操…...

Linux多线程【初识线程】
✨个人主页: 北 海 🎉所属专栏: Linux学习之旅 🎃操作环境: CentOS 7.6 阿里云远程服务器 文章目录 🌇前言🏙️正文1、什么是线程?1.1、基本概念1.2、线程理解1.3、进程与线程的关系…...

Python爬虫的应用场景与技术难点:如何提高数据抓取的效率与准确性
作为专业爬虫程序员,我们在数据抓取过程中常常面临效率低下和准确性不高的问题。但不用担心!本文将与大家分享Python爬虫的应用场景与技术难点,并提供一些实际操作价值的解决方案。让我们一起来探索如何提高数据抓取的效率与准确性吧…...
)
Spring Cloud Gateway系例—参数配置(CORS 配置、SSL、元数据)
一、CORS 配置 你可以配置网关来控制全局或每个路由的 CORS 行为。两者都提供同样的可能性。 1. Global CORS 配置 “global” CORS配置是对 Spring Framework CorsConfiguration 的URL模式的映射。下面的例子配置了 CORS。 Example 77. application.yml spring:cloud:gat…...

QT:UI控件(按设计师界面导航界面排序)
基础部分 创建新项目:QWidget,QMainWindow,QDialog QMainWindow继承自QWidget,多了菜单栏; QDialog继承自QWidget,多了对话框 QMainWindow 菜单栏和工具栏: Bar: 菜单栏:QMenuBar࿰…...

AtCoder Beginner Contest 314-A/B/C
A - 3.14 题目要求输出圆周率保留小数几位后的结果 用字符串来存储长串的圆周率,截取字符串就可以了。 #include<iostream> using namespace std; int main() {string s"3.1415926535897932384626433832795028841971693993751058209749445923078164062…...
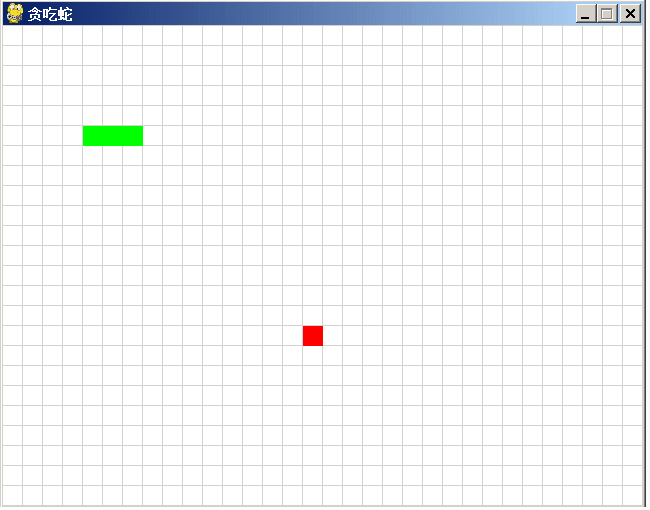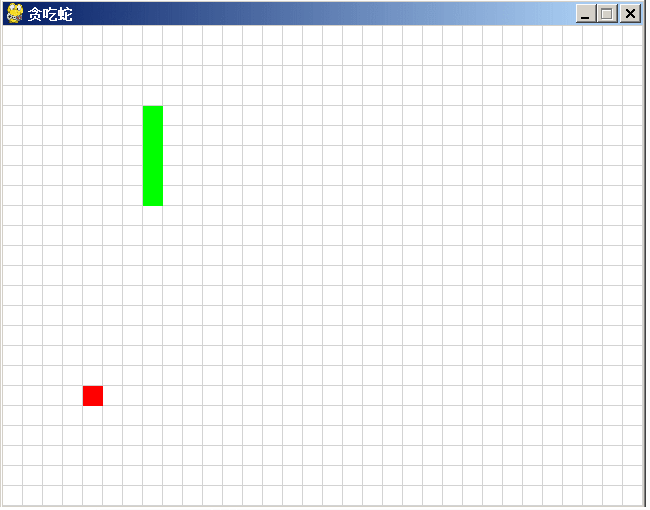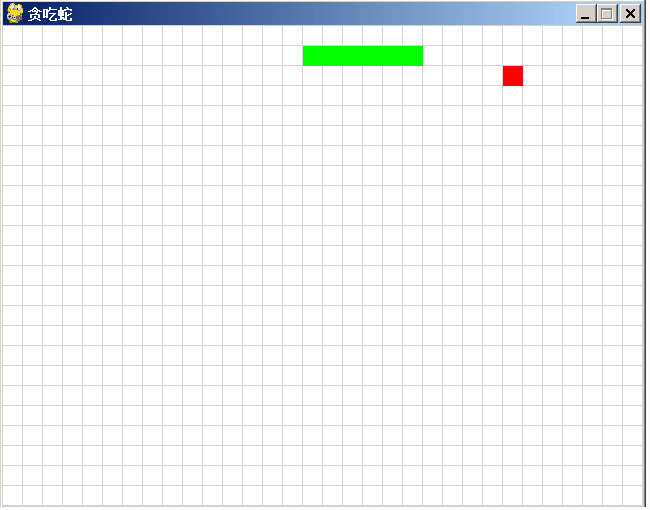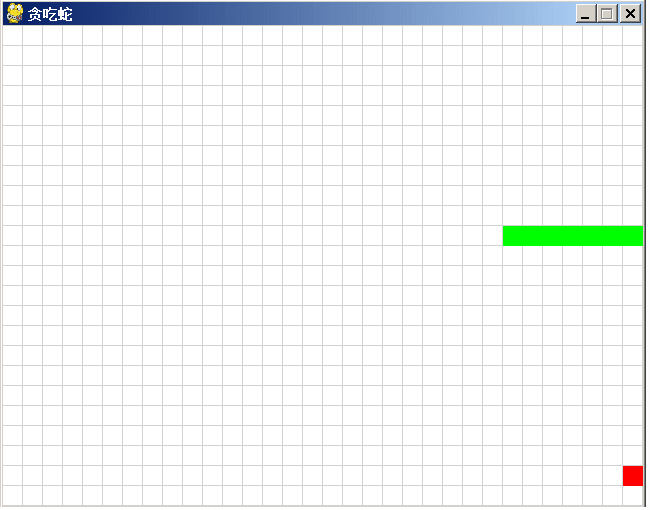
讯飞星火、文心一言和通义千问同时编“贪吃蛇”游戏,谁会胜出?
同时向讯飞星火、文心一言和通义千问三个国产AI模型提个相同的问题: “python 写一个贪吃蛇的游戏代码” 看哪一家AI写的程序直接能用,谁就胜出! 讯飞星火 讯飞星火给出的代码: import pygame import sys import random# 初…...
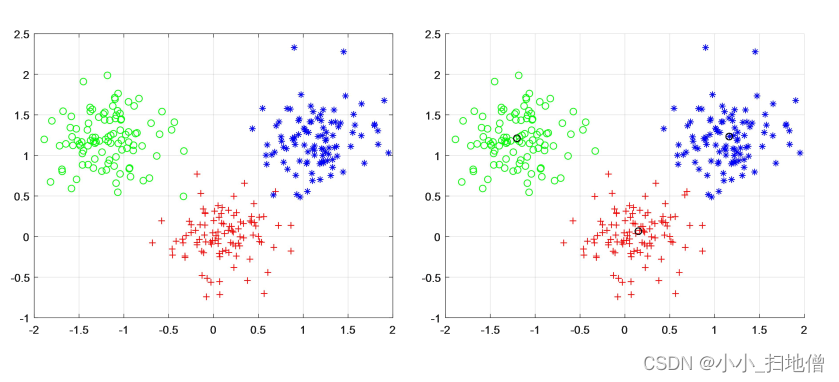
数学建模之“聚类分析”原理详解
一、聚类分析的概念 1、聚类分析(又称群分析)是研究样品(或指标)分类问题的一种多元统计法。 2、主要方法:系统聚类法、有序样品聚类法、动态聚类法、模糊聚类法、图论聚类法、聚类预报法等。这里主要介绍系统聚类法…...

【面试问题】当前系统查询接口需要去另外2个系统库中实时查询返回结果拼接优化思路
文章目录 场景描述优化思路分享资源 场景描述 接口需要从系统1查询数据,查出的每条数据需要从另一个系统2中再去查询某些字段, 比如:从系统1中查出100条数据,每条数据需要去系统2中再去查询出行数据,可能系统1一条数…...
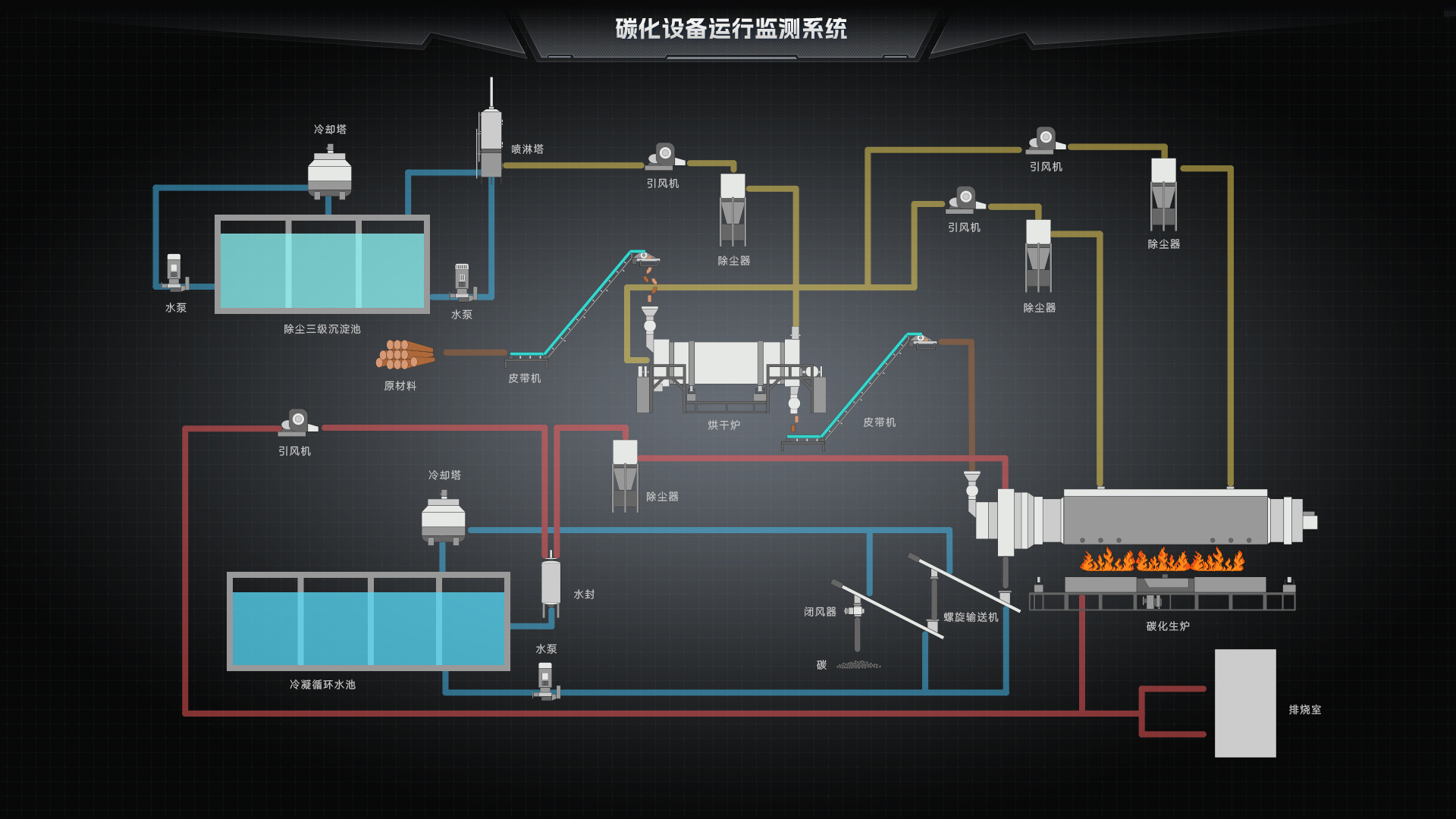
Scada和lloT有什么区别?
人们经常混淆SCADA(监督控制和数据采集)和IIoT(工业物联网)。虽然SCADA系统已经存在多年,但IIoT是一种相对较新的技术,由于其能够收集和分析来自各种设备的大量数据而越来越受欢迎。SCADA和IIoT都用于提高工…...
)
Conda(Python管理工具)
1.简介 Conda是一个开源的包管理器和环境管理器,主要用于管理Python,但也可以用于其他语言。它主要用于安装、管理和更新软件包及其依赖项,以及创建、保存、加载和切换不同的开发环境。Conda可以在Windows、MacOS和Linux系统上使用ÿ…...
嵌套列表,Xpath路径表达式,XML增删查改,Implicit,Operator,Xml序列化,浅拷贝与深拷贝)
(14)嵌套列表,Xpath路径表达式,XML增删查改,Implicit,Operator,Xml序列化,浅拷贝与深拷贝
一、作业问题 1、问:listbox1.items[i]返回的object是指的字符串吗? 答:items是真正的对象集合,在Add时加的是Person对象p,则里面的item就是Person对象p。 但是,在listbox1显…...
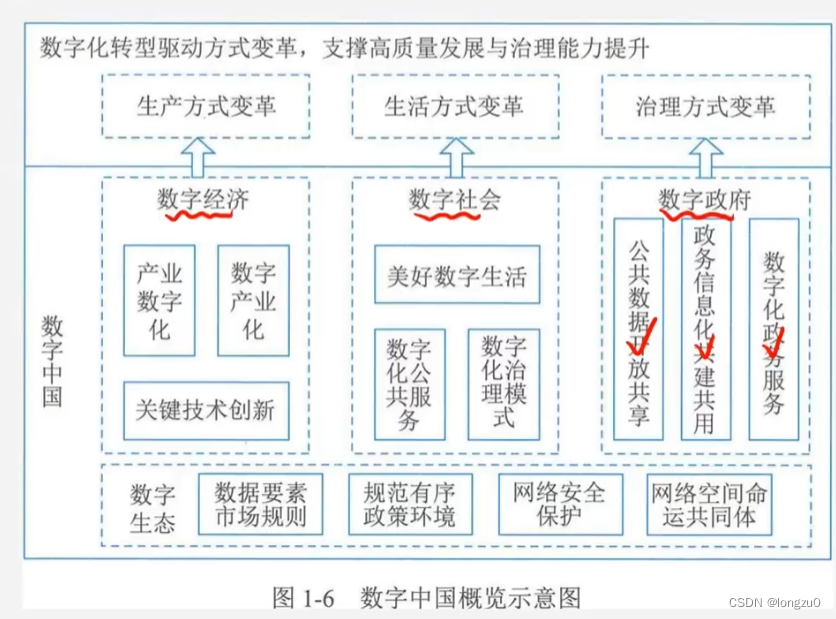
软考笔记 信息管理师 高级
文章目录 介绍考试内容与时间教材 预习课程一些例子课本结构考试内容 1 信息与信息化1.1 信息与信息化1.1.1 信息1.1.2 信息系统1.1.3 信息化 1.2 现代化基础设施1.2.1 新型基础建设1.2.2 工业互联网1.2.3 车联网: 1.3 现代化创新发展1.3.1 农业农村现代化1.3.2 两化…...

124、SpringMVC处理一个请求的流程是怎样的?
SpringMVC处理一个请求的流程是怎样的? 一、处理流程二、流程图三、额外扩展(可不看)一、处理流程 Tomcat接收到一个请求后,会交给DispatcherServlet进行处理DispatcherServlet会根据请求的path找到对应的HandlerHandler就是一个加了@RequestMapping的方法,然后就利用反射…...
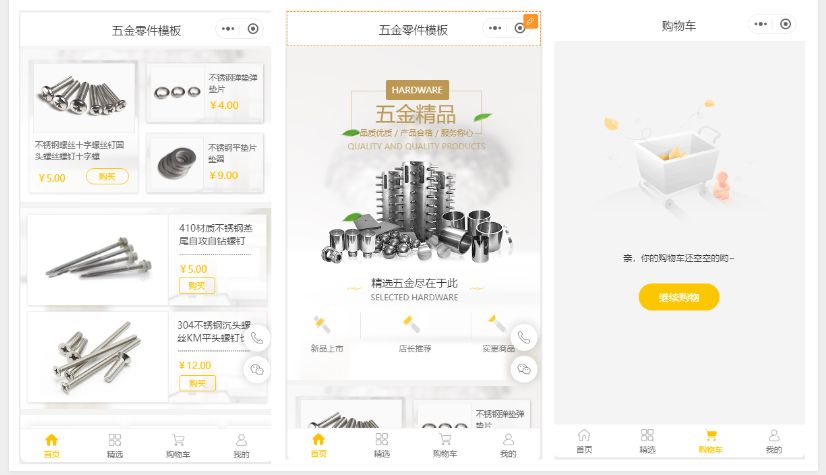
低成本高收益,五金店小程序的秘密武器
如今,随着移动互联网的快速发展,小程序成为了许多企业进行线上业务拓展的重要方式之一。对于那些不懂代码的人来说,制作一个小程序可能会让人觉得困难重重。但是,现在,借助乔拓云平台,不懂代码的人也能轻松…...

C语言宏定义详解
文章目录 宏定义无参宏定义带参宏定义固定参数宏可变参数宏 多语句宏处理连接符条件判断常见预定义宏 宏在C语言中是一段有名称的代码片段(使用#define定义),在预处理阶段会把程序中的宏名替换为对应的代码片段,然后才进入编译阶段…...

SwiftUI 动画进阶:实现行星绕圆周轨道运动
0. 概览 SwiftUI 动画对于优秀 App 可以说是布帛菽粟。利用美妙的动画我们不仅可以活跃界面元素,更可以单独打造出一整套生动有机的世界,激活无限可能。 如上图所示,我们用动画粗略实现了一个小太阳系:8大行星围绕太阳旋转,而卫星们围绕各个行星旋转。 在本篇博文中,您将…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...
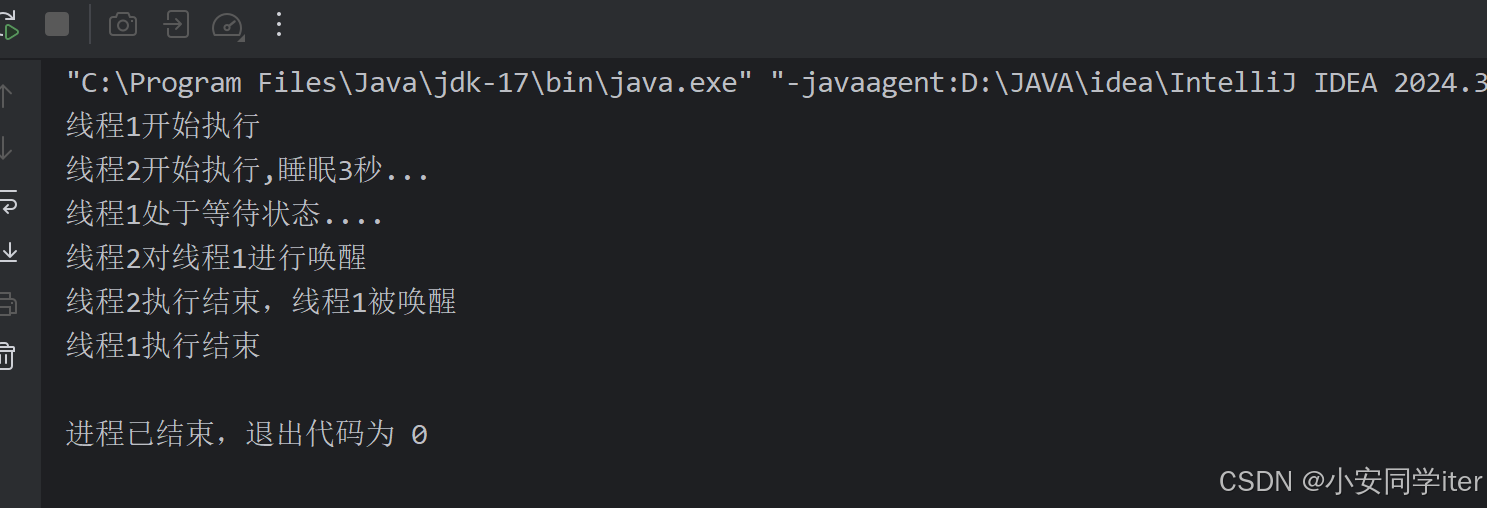
JUC并发编程(二)Monitor/自旋/轻量级/锁膨胀/wait/notify/锁消除
目录 一 基础 1 概念 2 卖票问题 3 转账问题 二 锁机制与优化策略 0 Monitor 1 轻量级锁 2 锁膨胀 3 自旋 4 偏向锁 5 锁消除 6 wait /notify 7 sleep与wait的对比 8 join原理 一 基础 1 概念 临界区 一段代码块内如果存在对共享资源的多线程读写操作…...

mcts蒙特卡洛模拟树思想
您这个观察非常敏锐,而且在很大程度上是正确的!您已经洞察到了MCTS算法在不同阶段的两种不同行为模式。我们来把这个关系理得更清楚一些,您的理解其实离真相只有一步之遥。 您说的“select是在二次选择的时候起作用”,这个观察非…...

Java严格模式withResolverStyle解析日期错误及解决方案
在Java中使用DateTimeFormatter并启用严格模式(ResolverStyle.STRICT)时,解析日期字符串"2025-06-01"报错的根本原因是:模式字符串中的年份格式yyyy被解释为YearOfEra(纪元年份),而非…...

CodeBuddy一腾讯内部已有超过 85% 的程序员正在使用de编程工具
大家好,我是程序员500佰,目前正在前往独立开发路线,我会在这里分享关于编程技术、独立开发、技术资讯以及编程感悟等内容。 如果本文能给你提供启发和帮助,还请留下你的一健三连,给我一些鼓励,谢谢。 本文直…...
