1572. 矩阵对角线元素的和
题目描述:
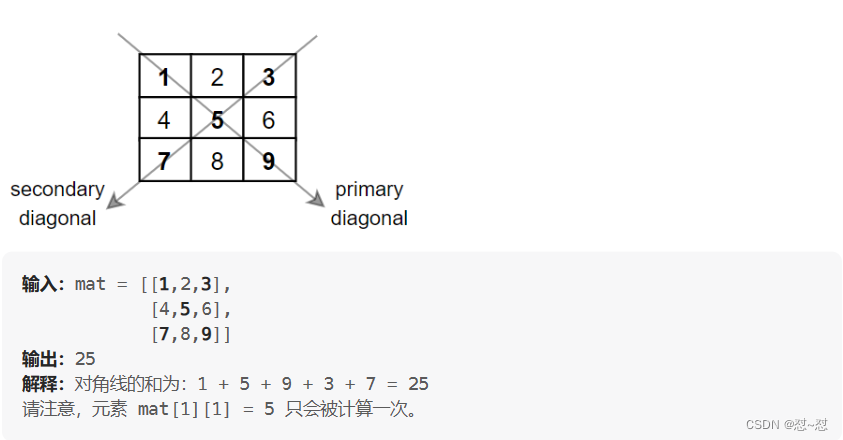
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
示例:


解题思路:
同时求对角线和副对角线上元素的和再减去重合的元素
相关代码:
class Solution {public int diagonalSum(int[][] mat) {int sum=0;for(int i=0;i<mat.length;i++) {sum+=mat[i][i]+mat[i][mat.length-i-1];}if(mat.length%2==1) sum-=mat[mat.length/2][mat.length/2];return sum;}
}
相关文章:

1572. 矩阵对角线元素的和
题目描述: 给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。 请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。 示例: 解题思路: 同时求对角线和副对角线上元素的和再减去重合的元素 相关代码…...

在vue中使用swiper轮播图(搭配watch和$nextTick())
在组件中使用轮播图展示图片信息: 1.下载swiper,5版本为稳定版本 cnpm install swiper5 2.在组件中引入swiper包和对应样式,若多组件使用swiper,可以把swiper引入到main.js入口文件中: import swiper/css/swiper.css //引入swipe…...

Java书签 #使用MyBatis接入多数据源
楔子:当然,世上有很多优秀的女性,我也会被她们吸引。这对男人来说是理所当然的。但目光被吸引和内心被吸引是截然不同的。- 东野圭吾《黎明之街》 今日书签 在一些应用场景中,可能需要连接多个不同的数据库,例如连接不…...

神经网络基础-神经网络补充概念-23-神经网络的梯度下降法
概念 神经网络的梯度下降法是训练神经网络的核心优化算法之一。它通过调整神经网络的权重和偏差,以最小化损失函数,从而使神经网络能够逐渐逼近目标函数的最优值。 步骤 1损失函数(Loss Function): 首先,…...
鸿蒙3.1 设备管理DeviceManager
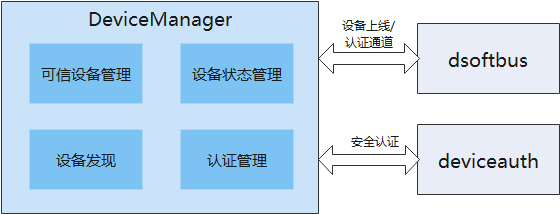
介绍 DeviceManager组件在OpenHarmony上提供账号无关的分布式设备的认证组网能力,并为开发者提供了一套用于分布式设备间监听、发现和认证的接口。 其组成及依赖如下所示: 总结 设备管理模块其实就是软总线的包皮服务。目前权限都是控制系统uid,但是根据官方介绍,后续可…...

Git 目录详解
一、Git目录详解 在使用Git时,有几个目录和文件在Git项目中扮演着重要的角色,下面详细介绍一下这些目录和文件的作用 1、.git目录 .git目录是Git项目的核心,包含了Git的版本库和元数据等重要信息。在该目录中,有一些重要的子目录和…...
基于springboot+vue的武汉旅游网(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

步入React正殿 - React组件设计模式
目录 扩展学习资料 高阶组件 /src/components/hoc/withTooltip.js /src/components/hoc/itemA.jsx /src/components/hoc/itemB.jsx /src/App.js 函数作为子组件【Render pprops】 函数作为子组件 /src/components/rp/itemC.jsx【父组件】 /src/components/rp/withToo…...

Java 单例模式简单介绍
何为单例模式 所谓类的单例设计模式,就是采取一定的方法保证在整个的软件系统中,对某个类只能存在一个对象实例,并且该类只提供一个取得其对象实例的方法。 实现思路 如果我们要让类在一个虚拟机中只能产生一个对象,我们首先必…...

根据源码,模拟实现 RabbitMQ - 从需求分析到实现核心类(1)
目录 一、需求分析 1.1、对 Message Queue 的认识 1.2、消息队列核心概念 1.3、Broker Server 内部关键概念 1.4、Broker Server 核心 API (重点实现) 1.5、交换机类型 Direct 直接交换机 Fanout 扇出交换机 Topic 主题交换机 1.6、持久化 1.7…...

企业服务器数据库遭到malox勒索病毒攻击后如何解决,勒索病毒解密
网络技术的发展不仅为企业带来了更高的效率,还为企业带来信息安全威胁,其中较为常见的就是勒索病毒攻击。近期,我们公司收到很多企业的求助,企业的服务器数据库遭到了malox勒索病毒攻击,导致系统内部的许多重要数据被加…...
udp与can通信的选择与比较
UDP(用户数据报协议)和CAN(控制器局域网)是两种不同的通信协议,它们在实时传递性上有一些区别。 UDP是一种无连接的传输协议,它提供了简单的、不可靠的数据传输。UDP不提供可靠性保证、流控制或重传机制。…...

HoudiniVex笔记_P24_ForceBasics力基础
原视频:https://www.youtube.com/playlist?listPLzRzqTjuGIDhiXsP0hN3qBxAZ6lkVfGDI Bili:Houdini最强VEX算法教程 - VEX for Algorithmic Design_哔哩哔哩_bilibili Houdini版本:19.5 1、什么是Force 本章主要讲重力、弹力、速度与质量、…...
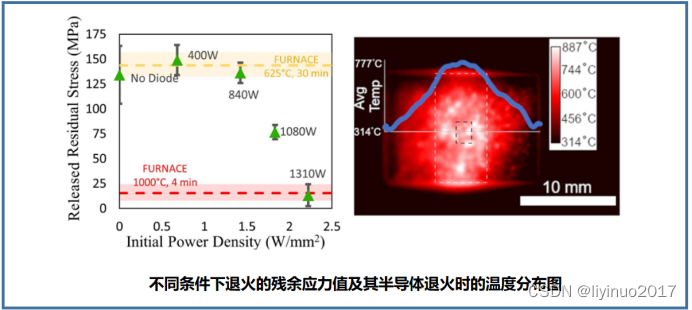
半导体退火那些事(1)
1.半导体退火的原理 半导体材料在晶体生长和制造过程中,由于各种原因会出现缺陷、杂质、位错等结构性缺陷,导致晶格不完整,施加电场后的电导率较低。通过退火处理,可以使材料得到修复,结晶体内部重新排列,…...
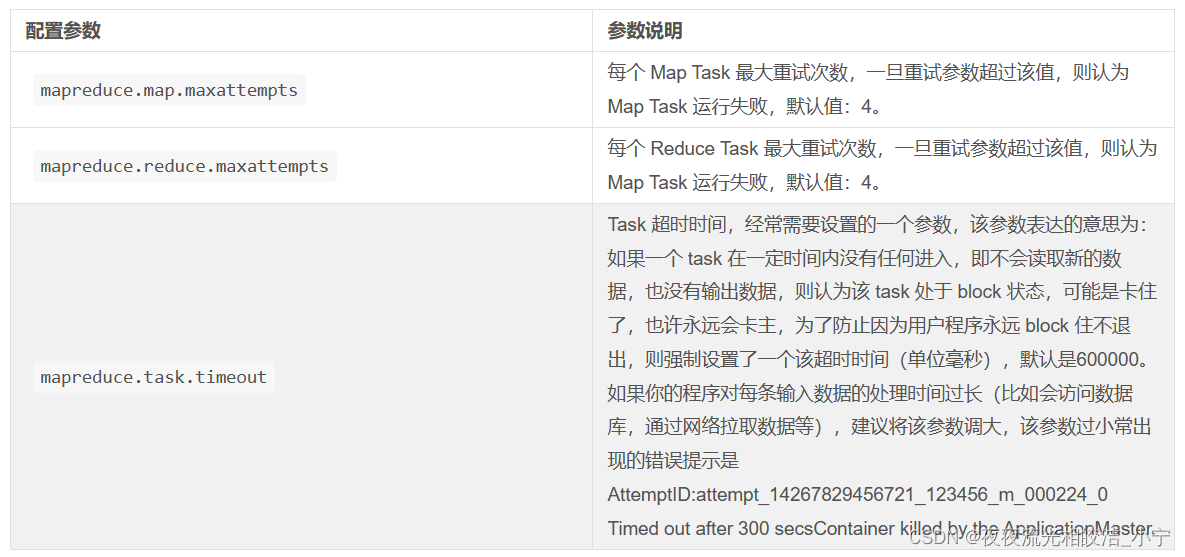
MapReduce介绍
目录 一、什么是MapReduce 二、MapReduce 的设计思想 2.1 分而治之 2.2 构建抽象模型:Map和Reduce 2.3 隐藏系统层细节 三、MapReduce 的框架原理 3.1 MRv1工作原理 3.1.1 MRv1架构工作原理图 3.1.1.1 流程说明 3.1.1.1.1 作业的提交 3.1.1.1.2 作业的初始化 3…...

Redis支持的主要数据结构操作命令有哪些?
Redis支持多种数据结构操作命令,包括以下主要命令: 字符串(Strings): SET:设置字符串键的值。GET:获取指定键的值。INCR/DECR:对存储整数的字符串执行加一或减一操作。APPEND&#x…...
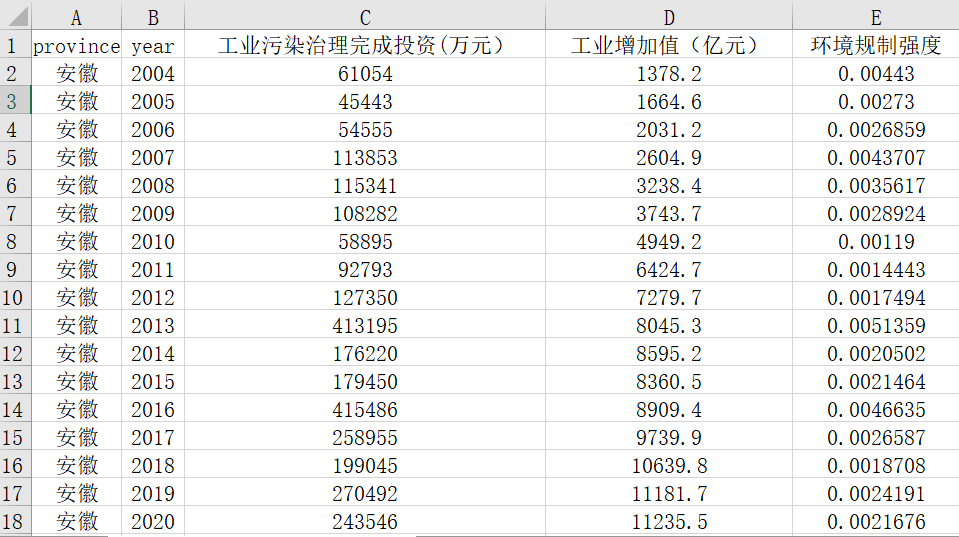
环境与能源创新专题:地级市绿色创新、碳排放与环境规制数据
数据简介:推动绿色发展,促进人与自然和谐共生是重大战略举措。绿色发展强调“绿水青山就是金山银山”,人与自然和谐共生重在正确处理生态环境保护与经济发展的关系。在着力于实现绿色发展的过程中,绿色创新是绿色发展的重要驱动因…...

设计模式之门面模式(Facade)的C++实现
1、门面模式提出 在组件的开发过程中,某些接口之间的依赖是比较紧密的,如果某个接口发生变化,其他的接口也会跟着发生变化,这样的代码违背了代码的设计原则。门面设计模式是在外部客户程序和系统程序之间添加了一层中间接口&…...
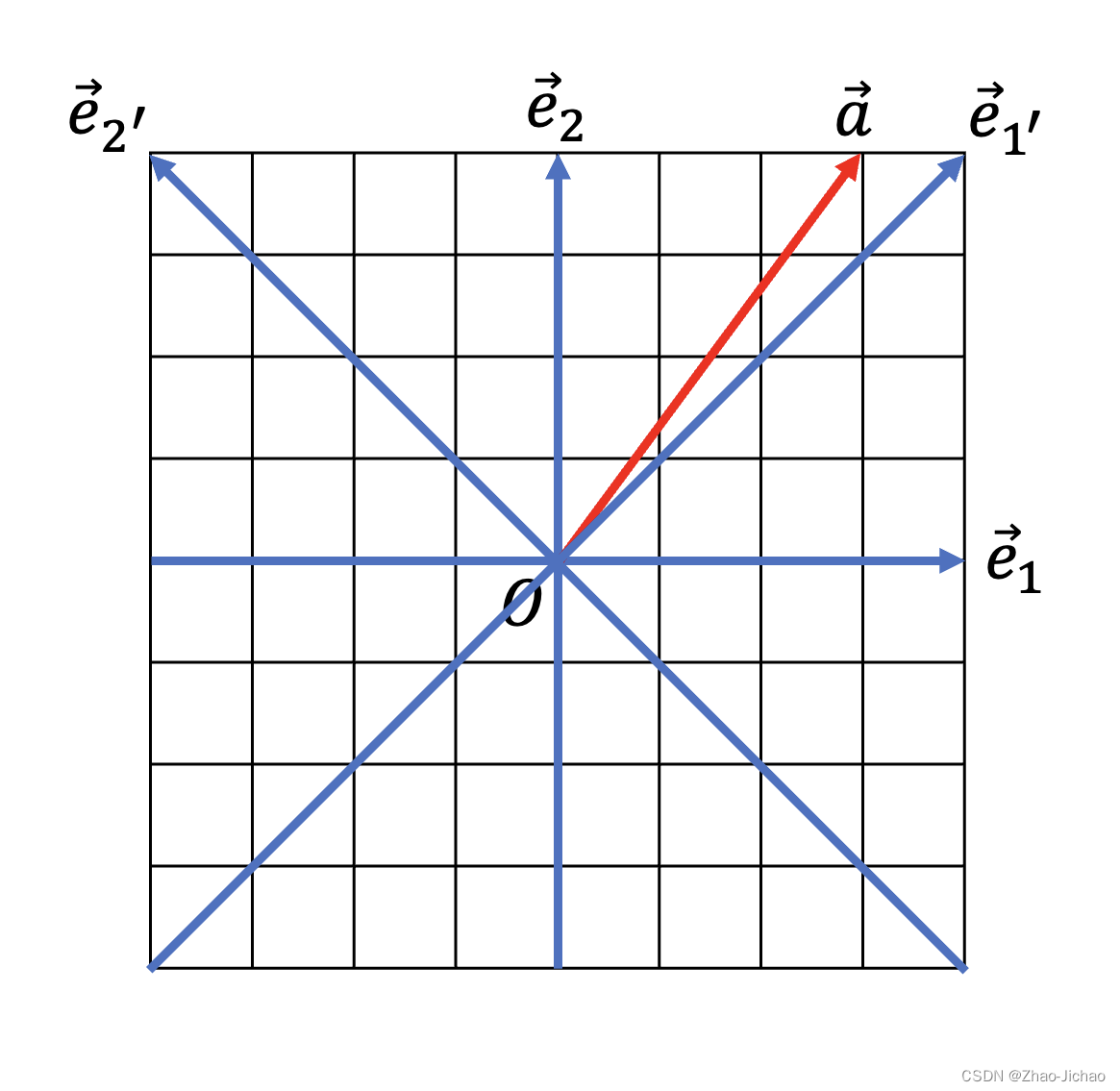
【数理知识】向量与基的内积,Matlab 代码验证
序号内容1【数理知识】向量的坐标基表示法,Matlab 代码验证2【数理知识】向量与基的内积,Matlab 代码验证 文章目录 1. 向量与基的内积2. 二维平面向量举例3. 代码验证Ref 1. 向量与基的内积 假设存在一个二维平面内的向量 a ⃗ \vec{a} a ,…...

黑客入侵:福特汽车Sync3车机存在漏洞,黑客入侵可抹除系统数据
据福特汽车公告,他们发现部分2021年至2022年车型的Sync3车机存在Wi-Fi漏洞,该漏洞可能被黑客利用来入侵并抹除车机内的系统数据。这一漏洞源于福特车系中采用的WL18xx MCP驱动程序的内存缓冲区溢位漏洞,其漏洞编号为CVE-2023-29468。 这一发现…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...
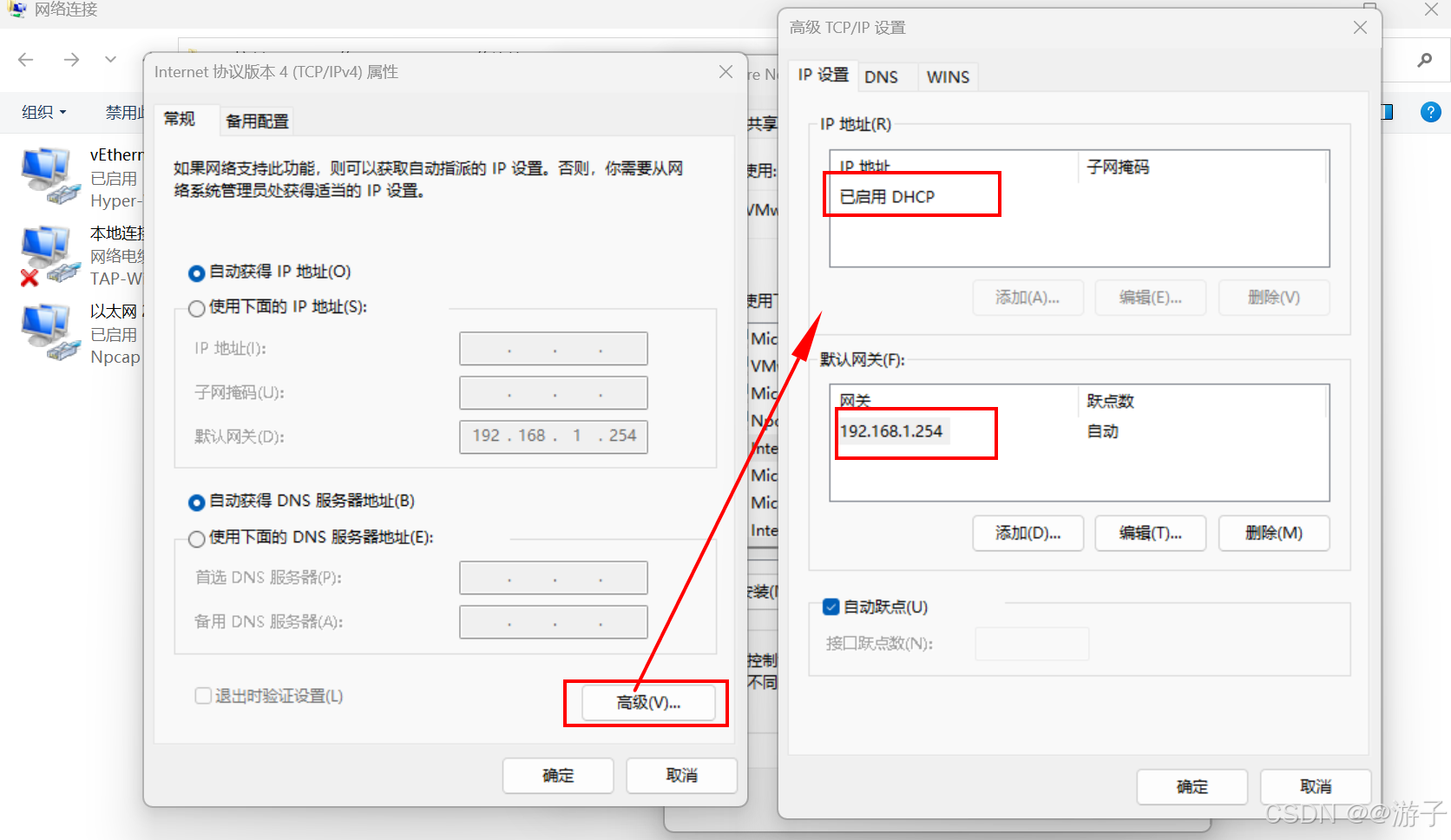
虚拟机网络不通的问题(这里以win10的问题为主,模式NAT)
当我们网关配置好了,DNS也配置好了,最后在虚拟机里还是无法访问百度的网址。 第一种情况: 我们先考虑一下,网关的IP是否和虚拟机编辑器里的IP一样不,如果不一样需要更改一下,因为我们访问百度需要从物理机…...

break 语句和 continue 语句
break语句和continue语句都具有跳转作用,可以让代码不按既有的顺序执行 break break语句用于跳出代码块或循环 1 2 3 4 5 6 for (var i 0; i < 5; i) { if (i 3){ break; } console.log(i); } continue continue语句用于立即终…...

C++ Saucer 编写Windows桌面应用
文章目录 一、背景二、Saucer 简介核心特性典型应用场景 三、生成自己的项目四、以Win32项目方式构建Win32项目禁用最大化按钮 五、总结 一、背景 使用Saucer框架,开发Windows桌面应用,把一个html页面作为GUI设计放到Saucer里,隐藏掉运行时弹…...
