【数理知识】向量与基的内积,Matlab 代码验证
| 序号 | 内容 |
|---|---|
| 1 | 【数理知识】向量的坐标基表示法,Matlab 代码验证 |
| 2 | 【数理知识】向量与基的内积,Matlab 代码验证 |
文章目录
- 1. 向量与基的内积
- 2. 二维平面向量举例
- 3. 代码验证
- Ref
1. 向量与基的内积
假设存在一个二维平面内的向量 a ⃗ \vec{a} a,其在坐标基 e ⃗ 1 , e ⃗ 2 \vec{e}_1, \vec{e}_2 e1,e2 下的坐标值为 [ x y ] \left[\begin{matrix}x \\ y \end{matrix}\right] [xy]。
我们这里先看一下向量 a ⃗ \vec{a} a 自身与坐标基 e ⃗ 1 \vec{e}_1 e1 的内积。关于内积的原理请参考文章【数理知识】向量数乘,内积,外积,matlab代码实现。这里我们直接使用其结论,即向量的内积为,一个向量在另一个向量方向上的投影长度,乘以被投影向量的长度,如下图所示

用公式描述为
a ⃗ ⋅ e ⃗ 1 = ∥ a ⃗ ∥ ∥ e ⃗ 1 ∥ cos ( θ ) \vec{a} \cdot \vec{e}_1 = \|\vec{a}\| \|\vec{e}_1\| \cos(\theta) a⋅e1=∥a∥∥e1∥cos(θ)
而在我们这里被投影向量为基向量 e ⃗ 1 \vec{e}_1 e1,而基向量 e ⃗ 1 \vec{e}_1 e1 其模长 ∥ e ⃗ 1 ∥ \|\vec{e}_1\| ∥e1∥ 又为 1 1 1,因此
a ⃗ ⋅ e ⃗ 1 = ∥ a ⃗ ∥ ∥ e ⃗ 1 ∥ cos ( θ ) = ∥ a ⃗ ∥ cos ( θ ) \begin{aligned} \vec{a} \cdot \vec{e}_1 &= \|\vec{a}\| \|\vec{e}_1\| \cos(\theta) \\ &= \|\vec{a}\| \cos(\theta) \end{aligned} a⋅e1=∥a∥∥e1∥cos(θ)=∥a∥cos(θ)
数值上 ∥ a ⃗ ∥ cos ( θ ) \|\vec{a}\| \cos(\theta) ∥a∥cos(θ) 等于向量 a ⃗ \vec{a} a 在坐标基 e ⃗ 1 \vec{e}_1 e1 上的坐标值。如果坐标基 e ⃗ 1 \vec{e}_1 e1 我们认为其为横坐标,那么 a ⃗ ⋅ e ⃗ 1 \vec{a} \cdot \vec{e}_1 a⋅e1 数值上就等于横坐标的值,即
a x = a ⃗ ⋅ e ⃗ 1 \begin{aligned} a_x &= \vec{a} \cdot \vec{e}_1 \end{aligned} ax=a⋅e1
同理,我们也可以得到 a ⃗ ⋅ e ⃗ 2 \vec{a} \cdot \vec{e}_2 a⋅e2 数值上等于纵坐标的值。
a y = a ⃗ ⋅ e ⃗ 2 \begin{aligned} a_y &= \vec{a} \cdot \vec{e}_2 \end{aligned} ay=a⋅e2
最后,公式化描述结论为
a x = a ⃗ ⋅ e ⃗ 1 = [ a x a y ] ⋅ [ e 11 e 12 ] = a x e 11 + a y e 12 a y = a ⃗ ⋅ e ⃗ 2 = [ a x a y ] ⋅ [ e 21 e 22 ] = a x e 21 + a y e 22 , ∥ e ⃗ 1 ∥ = ∥ e ⃗ 2 ∥ = 1 \begin{aligned} a_x &= \vec{a} \cdot \vec{e}_1 =\left[\begin{matrix} a_x \\ a_y \\ \end{matrix}\right] \cdot \left[\begin{matrix} e_{11} \\ e_{12} \\ \end{matrix}\right] =a_x e_{11} + a_y e_{12} \\ a_y &= \vec{a} \cdot \vec{e}_2 =\left[\begin{matrix} a_x \\ a_y \\ \end{matrix}\right] \cdot \left[\begin{matrix} e_{21} \\ e_{22} \\ \end{matrix}\right] =a_x e_{21} + a_y e_{22} \end{aligned},\quad \|\vec{e}_1\| = \|\vec{e}_2\| = 1 axay=a⋅e1=[axay]⋅[e11e12]=axe11+aye12=a⋅e2=[axay]⋅[e21e22]=axe21+aye22,∥e1∥=∥e2∥=1
2. 二维平面向量举例
接下来基于二维平面上的一个向量来举例。
假设存在一个上述的二维平面向量 a ⃗ \vec{a} a,在标准坐标基 e ⃗ 1 = [ 1 0 ] , e ⃗ 2 = [ 0 1 ] \vec{e}_1=\left[\begin{matrix} 1 \\ 0 \\ \end{matrix}\right], \vec{e}_2=\left[\begin{matrix} 0 \\ 1 \\ \end{matrix}\right] e1=[10],e2=[01] 下的坐标值为 [ a x a y ] = [ 3 4 ] \left[\begin{matrix}a_x \\ a_y \end{matrix}\right] = \left[\begin{matrix}3 \\ 4 \end{matrix}\right] [axay]=[34]。
现在,我们更改坐标基为 e ⃗ 1 ′ = [ 1 2 1 2 ] , e ⃗ 2 ′ = [ − 1 2 1 2 ] \vec{e}_{1^\prime}=\left[\begin{matrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ \end{matrix}\right], \vec{e}_{2^\prime}=\left[\begin{matrix} -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ \end{matrix}\right] e1′=[2121],e2′=[−2121],此新基下的坐标值为 [ a x ′ a y ′ ] = [ 7 2 1 2 ] \left[\begin{matrix}a_{x^\prime} \\ a_{y^\prime} \end{matrix}\right] = \left[\begin{matrix} \frac{7}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{matrix}\right] [ax′ay′]=[2721]。
首先验证结论
a x = a ⃗ ⋅ e ⃗ 1 = [ a x a y ] ⋅ [ e 11 e 12 ] = a x e 11 + a y e 12 = [ 3 4 ] ⋅ [ 1 0 ] = 3 × 1 + 4 × 0 = 3 \begin{aligned} a_x &= \vec{a} \cdot \vec{e}_1 =\left[\begin{matrix} a_x \\ a_y \\ \end{matrix}\right] \cdot \left[\begin{matrix} e_{11} \\ e_{12} \\ \end{matrix}\right] =a_x e_{11} + a_y e_{12} \\ &= \left[\begin{matrix} 3 \\ 4 \\ \end{matrix}\right] \cdot \left[\begin{matrix} 1 \\ 0 \\ \end{matrix}\right] = 3 \times 1 + 4 \times 0 = 3 \end{aligned} ax=a⋅e1=[axay]⋅[e11e12]=axe11+aye12=[34]⋅[10]=3×1+4×0=3
a x ′ = a ⃗ ⋅ e ⃗ 1 ′ = [ a x a y ] ⋅ [ e 1 1 ′ e 1 2 ′ ] = a x e 1 1 ′ + a y e 1 2 ′ = [ 3 4 ] ⋅ [ 1 2 1 2 ] = 3 × 1 2 + 4 × 1 2 = 7 2 \begin{aligned} a_{x^\prime} &= \vec{a} \cdot \vec{e}_{1^\prime} =\left[\begin{matrix} a_{x} \\ a_{y} \\ \end{matrix}\right] \cdot \left[\begin{matrix} e_{11^\prime} \\ e_{12^\prime} \\ \end{matrix}\right] =a_{x} e_{11^\prime} + a_{y} e_{12^\prime} \\ &= \left[\begin{matrix} 3 \\ 4 \\ \end{matrix}\right] \cdot \left[\begin{matrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ \end{matrix}\right] = 3 \times \frac{1}{\sqrt{2}} + 4 \times \frac{1}{\sqrt{2}} = \frac{7}{\sqrt{2}} \end{aligned} ax′=a⋅e1′=[axay]⋅[e11′e12′]=axe11′+aye12′=[34]⋅[2121]=3×21+4×21=27
通过观察下图,也能大约看出向量 a ⃗ \vec{a} a 在新基 e ⃗ 1 ′ \vec{e}_{1^\prime} e1′ 上的投影长度为 7 / 2 7/\sqrt{2} 7/2。
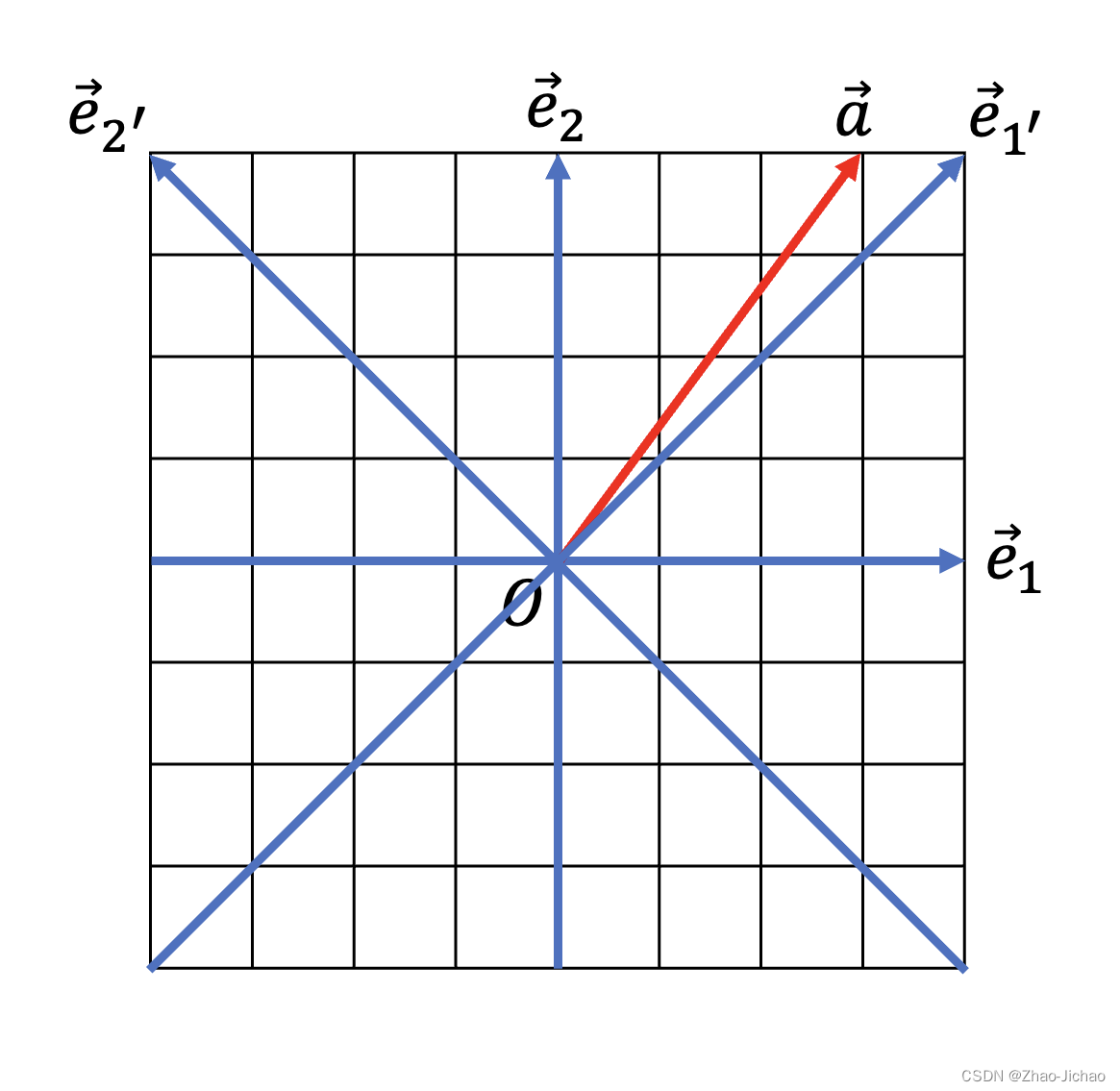
这与坐标图中的效果也是一致的。
往下继续验证结论
a y = a ⃗ ⋅ e ⃗ 2 = [ a x a y ] ⋅ [ e 21 e 22 ] = a x e 21 + a y e 22 = [ 3 4 ] ⋅ [ 0 1 ] = 3 × 0 + 4 × 1 = 4 \begin{aligned} a_y &= \vec{a} \cdot \vec{e}_2 =\left[\begin{matrix} a_x \\ a_y \\ \end{matrix}\right] \cdot \left[\begin{matrix} e_{21} \\ e_{22} \\ \end{matrix}\right] =a_x e_{21} + a_y e_{22} \\ &= \left[\begin{matrix} 3 \\ 4 \\ \end{matrix}\right] \cdot \left[\begin{matrix} 0 \\ 1 \\ \end{matrix}\right] = 3 \times 0 + 4 \times 1 = 4 \end{aligned} ay=a⋅e2=[axay]⋅[e21e22]=axe21+aye22=[34]⋅[01]=3×0+4×1=4
a y ′ = a ⃗ ⋅ e ⃗ 2 ′ = [ a x a y ] ⋅ [ e 1 1 ′ e 1 2 ′ ] = a x e 1 1 ′ + a y e 1 2 ′ = [ 3 4 ] ⋅ [ − 1 2 1 2 ] = 3 × ( − 1 2 ) + 4 × 1 2 = 1 2 \begin{aligned} a_{y^\prime} &= \vec{a} \cdot \vec{e}_{2^\prime} =\left[\begin{matrix} a_{x} \\ a_{y} \\ \end{matrix}\right] \cdot \left[\begin{matrix} e_{11^\prime} \\ e_{12^\prime} \\ \end{matrix}\right] =a_{x} e_{11^\prime} + a_{y} e_{12^\prime} \\ &= \left[\begin{matrix} 3 \\ 4 \\ \end{matrix}\right] \cdot \left[\begin{matrix} -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ \end{matrix}\right] = 3 \times (-\frac{1}{\sqrt{2}}) + 4 \times \frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \end{aligned} ay′=a⋅e2′=[axay]⋅[e11′e12′]=axe11′+aye12′=[34]⋅[−2121]=3×(−21)+4×21=21
第二个结论同样意味着向量 a ⃗ \vec{a} a 在新基 e ⃗ 2 ′ \vec{e}_{2^\prime} e2′ 上的投影长度为 1 / 2 1/\sqrt{2} 1/2。
3. 代码验证
a_x = 3;
a_y = 4;
a = [a_xa_y];e_1 = [ 10];
e_2 = [ 01];e_1_prime = [ sqrt(2)/2sqrt(2)/2];
e_2_prime = [-sqrt(2)/2sqrt(2)/2];
>> dot(a, e_1)
ans =3>> dot(a, e_2)
ans =4>> dot(a, e_1_prime)
ans =4.9497>> dot(a, e_2_prime)
ans =0.7071
Ref
相关文章:

【数理知识】向量与基的内积,Matlab 代码验证
序号内容1【数理知识】向量的坐标基表示法,Matlab 代码验证2【数理知识】向量与基的内积,Matlab 代码验证 文章目录 1. 向量与基的内积2. 二维平面向量举例3. 代码验证Ref 1. 向量与基的内积 假设存在一个二维平面内的向量 a ⃗ \vec{a} a ,…...

黑客入侵:福特汽车Sync3车机存在漏洞,黑客入侵可抹除系统数据
据福特汽车公告,他们发现部分2021年至2022年车型的Sync3车机存在Wi-Fi漏洞,该漏洞可能被黑客利用来入侵并抹除车机内的系统数据。这一漏洞源于福特车系中采用的WL18xx MCP驱动程序的内存缓冲区溢位漏洞,其漏洞编号为CVE-2023-29468。 这一发现…...
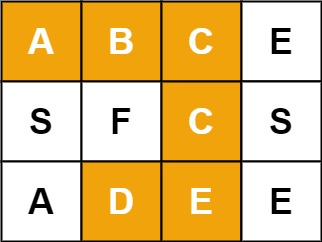
面试热题(单词搜索)
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。 单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相…...
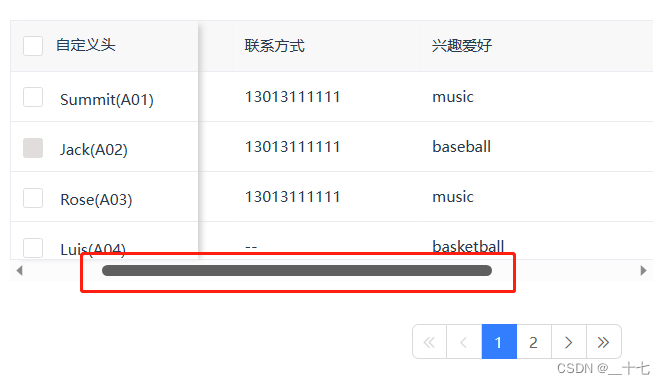
自定义表格组件:实现表格中有固定列的功能逻辑
目录 1,效果图2,实现思路3,实现方式 1,效果图 可以拖动纵向滑块,最左边一列固定住。 以同样的道理,可以在右面固定一列 2,实现思路 作为一个table组件,要接受父组件中的对table的…...

uni-app弹窗列表滚动, 弹框下面的内容也跟随滚动解决方案
滑动弹窗里的列表,弹框下面的内容也会跟着滑动,导致弹窗中的列表不能正常滚动 1.弹窗组件代码,需要在最外层的view中加入touchmove.stop.prevent"moveHandle",且弹窗中需要滚动的列表要使用scroll-view标签包裹起来&…...

Django操作cookie、Django操作session、Django中的Session配置、CBV添加装饰器、中间件、csrf跨站请求
一、Django操作cookie cookie的原理cookie的工作原理是:由服务器产生内容,浏览器收到请求后保存在本地;当浏览器再次访问时,浏览器会自动带上Cookie,这样服务器就能通过Cookie的内容来判断这个是“谁”了。1.设置cook…...
内网穿透——使用Windows自带的网站程序建立网站
文章目录 1.前言2.Windows网页设置2.1 Windows IIS功能设置2.2 IIS网页访问测试 3. Cpolar内网穿透3.1 下载安装Cpolar3.2 Cpolar云端设置3.3 Cpolar本地设置 4.公网访问测试5.结语 1.前言 在网上各种教程和介绍中,搭建网页都会借助各种软件的帮助,比如…...

JavaScript请求数据的4种方法总结(Ajax、fetch、jQuery、axios)
JavaScript请求数据有4种主流方式,分别是Ajax、fetch、jQuery和axios。 一、Ajax、fetch、jQuery和axios的详细解释: 1、 Ajax Ajax(Asynchronous JavaScript and XML)是一种使用JavaScript在用户的浏览器上发送请求的技术&…...

js中的break和continue中的区别
js中break和continue有着一些差别。 首先,虽然break和continue都有跳出循环的作用,但break是完全跳出循环,而continue则是跳出一次循环,然后开启下一次的循环。 下面我就来举几个例子吧。 var num 0;for(var i 1;i < 10;i){i…...
Cat(2):下载与安装
1 github源码下载 要安装CAT,首先需要从github上下载最新版本的源码。 官方给出的建议如下: 注意cat的3.0代码分支更新都发布在master上,包括最新文档也都是这个分支注意文档请用最新master里面的代码文档作为标准,一些开源网站…...

程序崩溃生成dump文件定位到崩溃处
#include <DbgHelp.h> #pragma comment(lib,"Dbghelp.lib")long __stdcall CrashInfocallback(_EXCEPTION_POINTERS* pexcp) {// 创建dmp文件HANDLE hDumpFile ::CreateFile(L"Memory.DMP",GENERIC_WRITE,0,NULL,CREATE_ALWAYS,FILE_ATTRIBUTE_NORM…...

安卓获取当前的IP地址
文章目录 获取IP地址完整示例代码 获取IP地址 在安卓中,我们使用静态方法NetworkInterface.getNetworkInterfaces() 来获取当前设备上所有的网络接口。 网络接口是指设备上用于进行网络通信的硬件或软件。这些接口可以是物理接口(如以太网接口、无线网…...

Pyqt5-自动化电池监测工具
开源第二篇,书接上回,上回的工具用起来着实不方便,功能也少,不能满足大部分需求,体现在:钉钉发送数据,数据处理,以及接收数据,定时任务等这部分。 随后对其进行了优化 数…...

Struts2一次请求参数问题的记录
最近,一次前端正常请求,但后台出现请求参数值的变化,导致报错,问题如下: 从入参request中查看请求参数,是一个Json字符串,其中有个description的键值对; 但是,接下来调用…...
ctfshow-web9
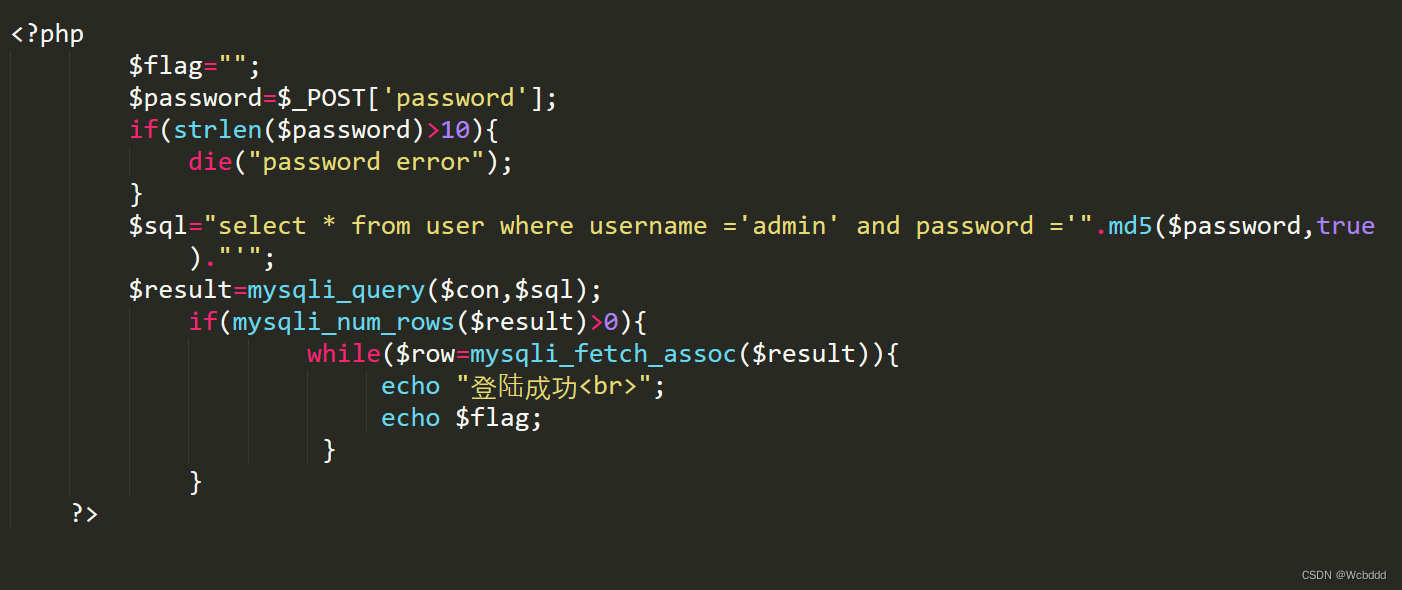
0x00 前言 CTF 加解密合集CTF Web合集 0x01 题目 0x02 Write Up 拿到一个站的时候一定要看robots.txt文件 访问一下 看到一个phps,然后下载一下 看到md5,参考这个https://blog.csdn.net/HAI_WD/article/details/132345156?spm1001.2014.3001.5501 …...

网络安全(黑客)自学路线/笔记
想自学网络安全(黑客技术)首先你得了解什么是网络安全!什么是黑客! 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全…...

Vim基本使用
Vim基本使用 概念模式类型常规模式编辑模式命令模式 概念 vim 是一款功能丰富、高度可定制和高效的文本编辑器,适用于处理各种文本文件和编程任务。熟练使用vim帮助提高编辑效率,并为用户提供更多的操作选项。 模式类型 常规模式 使用vim打开一个文件…...

二 根据用户行为数据创建ALS模型并召回商品
二 根据用户行为数据创建ALS模型并召回商品 2.0 用户行为数据拆分 方便练习可以对数据做拆分处理 pandas的数据分批读取 chunk 厚厚的一块 相当大的数量或部分 import pandas as pd reader pd.read_csv(behavior_log.csv,chunksize100,iteratorTrue) count 0; for chunk in …...

SpringBoot ⽇志⽂件
日志 1. 作用2. 日志的使用3. 日志的级别4. 日志的持久化 1. 作用 日志最主要的⽤途就是排除和定位问题。 除了发现和定位问题之外,我们还可以通过⽇志实现以下功能: 记录⽤户登录⽇志,⽅便分析⽤户是正常登录还是恶意破解⽤户。记录系统的…...

SpringBoot案例-部门管理-查询
查看页面原型,明确需求需求 页面原型 需求分析 阅读接口文档 接口文档链接如下: https://docs.qq.com/doc/DUkRiTWVaUmFVck9N 思路分析 用户发送请求,交由对应的Controller类进行处理,Controller类调用service实现查询部门功…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
