2023年国赛数学建模思路 - 案例:最短时间生产计划安排
文章目录
- 0 赛题思路
- 1 模型描述
- 2 实例
- 2.1 问题描述
- 2.2 数学模型
- 2.2.1 模型流程
- 2.2.2 符号约定
- 2.2.3 求解模型
- 2.3 相关代码
- 2.4 模型求解结果
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
最短时间生产计划模型
该模型出现在好几个竞赛赛题上,预测2023今年国赛也会与该模型相关。
1 模型描述
离散系统仿真在工业生产的工序安排中起到了相当重要的作用,如何就一些内部机制复杂的离散问题建立简单易行、可监测性强的数学模型一直是仿真技术的研究热点.
离散事件系统现有三种仿真建模策略,即:
- 事件调度法
- 活动扫描法
- 进程交互法.
该模型demo学长采用了其中的活动扫描法对生产中的一个实际例子进行了处理.
活动扫描法对于各事件之间相关性很强的系统有着很好的适用性.
2 实例
2.1 问题描述
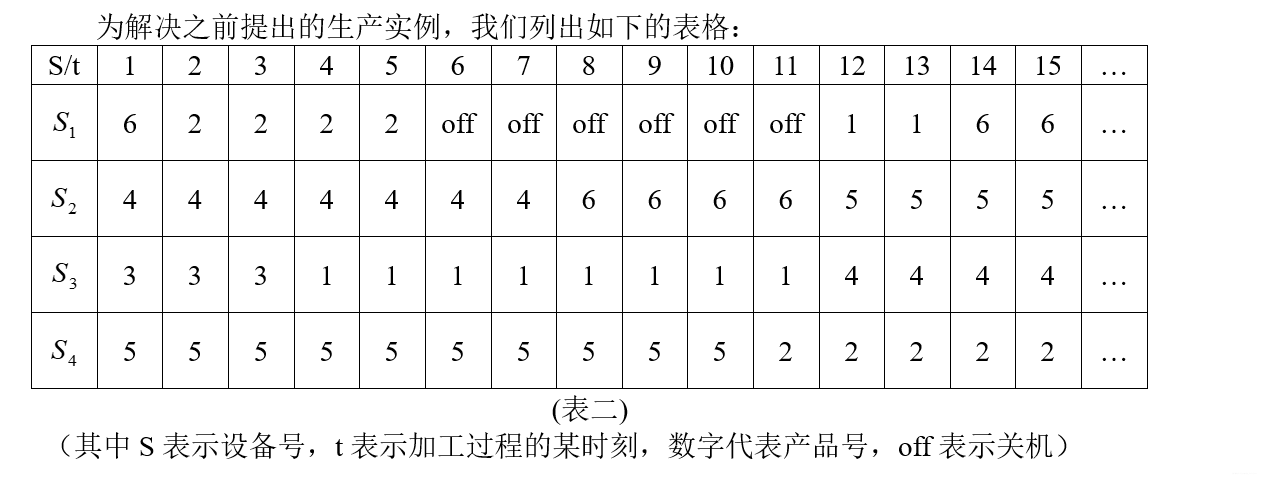
在许多工厂生产过程中,由于设备的数量、产品加工的次序限制,往往不能简单地安排生产任务.我们设想,应用强大的数学软件配合简单易行的方法进行安排.
设某重型机械厂产品都是单件性的,其中有一车间共有4种不同设备,现接受6件产品的加工任务,每件产品接受的程序在指定的设备上加工,其工序与加工周期如下表

现在我们根据这一实际问题,寻求安排的方法.
要求:
1、每件产品必须按规定的工序加工,不得颠倒.
2、每台设备在同一时间只能担任一项任务(每件产品的每个工序为一个任务).
3、在尽可能短的时间里,完成所接受的全部任务.
为了节省电能,合理分配生产任务,厂方还要求:
1、做出每件产品的每个工序开工、完工时间表.
2、给出每台设备承担任务的时间表.
2.2 数学模型
2.2.1 模型流程

2.2.2 符号约定

2.2.3 求解模型
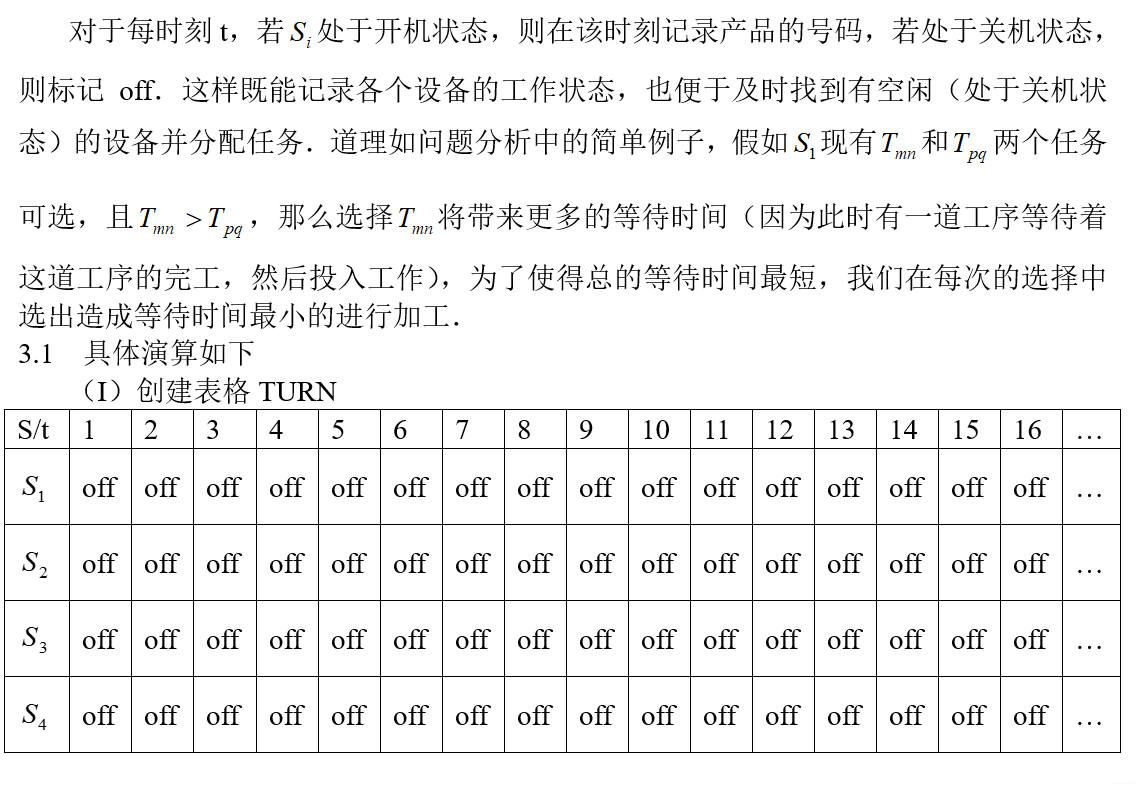
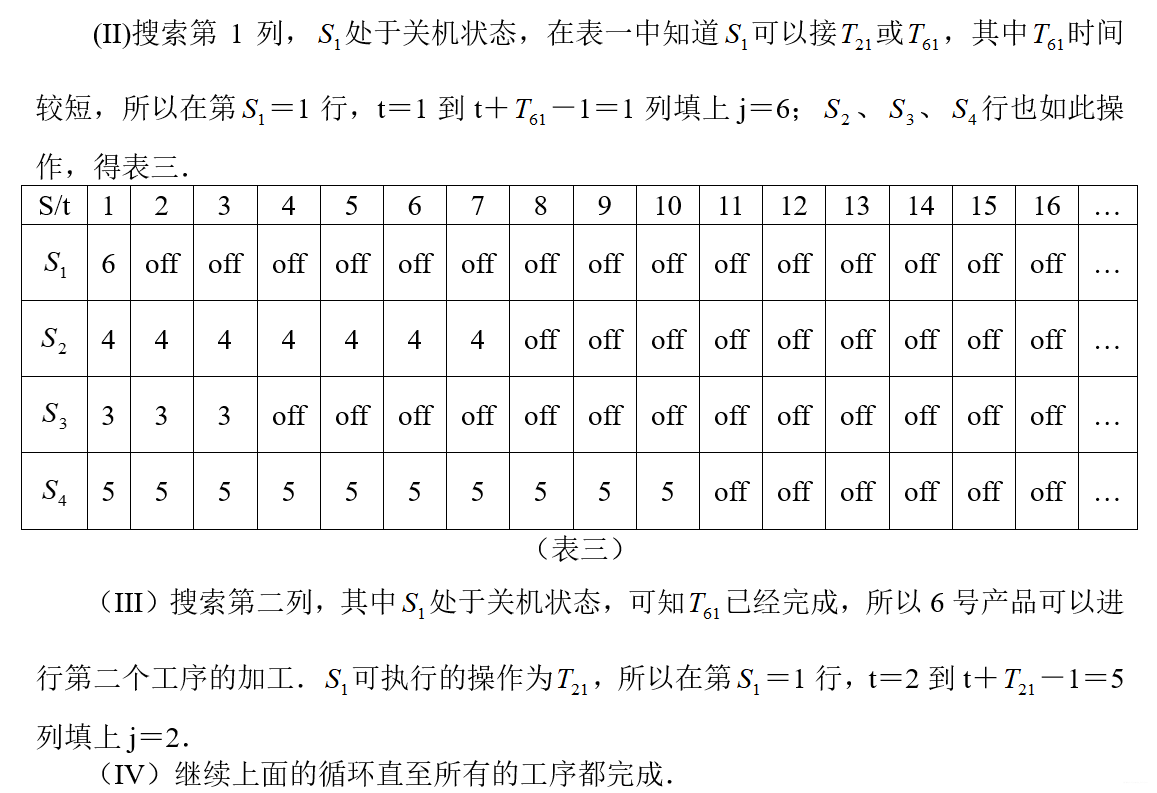
2.3 相关代码
clear
clc
seq=[3 1 2 3 4 0 0 0 %各产品加工时所用的设备的次序1 4 2 3 0 0 0 03 4 1 2 1 0 0 02 3 4 1 4 3 0 04 2 3 4 1 3 4 01 2 1 3 4 1 3 1];tim=[8 2 4 24 6 0 0 0 %加工对应使用的时间4 5 3 4 0 0 0 03 7 15 20 8 0 0 07 6 21 1 16 3 0 010 4 8 4 12 6 1 01 4 7 3 5 2 5 8];
whole=[0 0 0 0];
for i=1:6for j=1:8if(seq(i,j)~=0)whole(seq(i,j))=whole(seq(i,j))+tim(i,j);endend
end
whole %生产各件产品所需的总时间mes=cell(4,1); %记录各个设备的工作时间(对应于上面tim的位置)
for k=1:4mes{k,1}=zeros(6,8);for j=1:8for i=1:6if(seq(i,j)==k)mes{k,1}(i,j)=tim(i,j);elsemes{k,1}(i,j)=100;endendend
endturn=cell(5,100); %记录四个设备的开关时间及加工对象(on(i))
for i=1:4for j=1:100turn{i,j}='off';end
end
for i=1:100turn{5,i}=[num2str(i) '分'];
endopen=zeros(6,8);
%记录6个产品的加工进度,0表示未进行,1表示已开始(或已结束),2表示可选,3表示没有这个程序
for i=1:6open(i,1)=2;
end
for i=1:6for j=1:8if seq(i,j)==0open(i,j)=3;endend
endgongxu=zeros(6,1);
dai=zeros(4,1);
j=1;
s=[1 1 1 1 1 3 3 3
1 1 1 1 3 3 3 3
1 1 1 1 1 3 3 3
1 1 1 1 1 1 3 3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1];
while isequal(open,s)==0on=[];for i=1:4if turn{i,j}=='off'
%在turn矩阵中逐列搜索,若设备处于关机状态,则作记录(可用)on=[on i];endendl1=length(on);for m=1:l1 %在整个生产计划中(对设备逐个)寻找能够选作操作的步骤[x,y]=find(open==2);l2=length(x);a=[x(1) y(1)];for k=1:l2 %对某个设备on(m),找出当前它能操作的步骤中耗时最小的一个if mes{on(m)}(a(1),a(2))>mes{on(m)}(x(k),y(k))a=[x(k) y(k)];endendif turn{on(m),j}=='off' & mes{on(m)}(a(1),a(2))~=100
%若时间为100则意味着这个步骤不属于我们希望使用的那件设备while tim(a(1),a(2))>0turn{on(m),tim(a(1),a(2))+j-1}=a(1);tim(a(1),a(2))=tim(a(1),a(2))-1;endendendfor i=1:4if turn{i,j}~='off'dai(i)=turn{i,j};endendfor i=1:4if turn{i,j}~='off' & turn{i,j+1}=='off'gongxu(turn{i,j})=gongxu(turn{i,j})+1;open(turn{i,j},gongxu(turn{i,j}))=1;endif gongxu(dai(i))<8 & open(dai(i),gongxu(dai(i))+1)~=3 & turn{i,j+1}=='off'open(dai(i),gongxu(dai(i))+1)=2;endendj=j+1;
end2.4 模型求解结果
每件产品的每个工序开工、完工时间表

每台设备承担任务的时间表
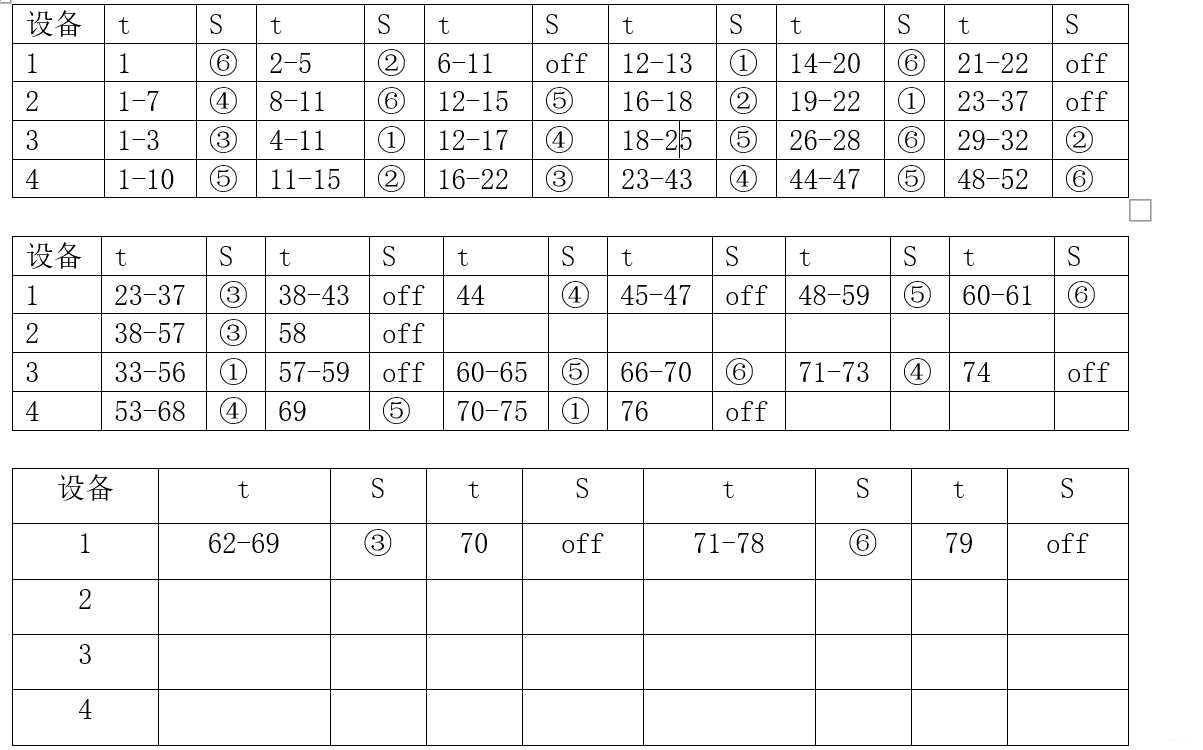
从结果中我们可以看到,使用这种方法,只需78个单位时间就可以完成所有的工序.而我们同时也可以在论文的开始部分看到,单就完成 就需耗费75个单位时间.可见这种方法得出的结果还是相当使人满意的,而且操作简单,可监测性强.
建模资料
资料分享: 最强建模资料


相关文章:

2023年国赛数学建模思路 - 案例:最短时间生产计划安排
文章目录 0 赛题思路1 模型描述2 实例2.1 问题描述2.2 数学模型2.2.1 模型流程2.2.2 符号约定2.2.3 求解模型 2.3 相关代码2.4 模型求解结果 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 最短时…...

1572. 矩阵对角线元素的和
题目描述: 给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。 请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。 示例: 解题思路: 同时求对角线和副对角线上元素的和再减去重合的元素 相关代码…...

在vue中使用swiper轮播图(搭配watch和$nextTick())
在组件中使用轮播图展示图片信息: 1.下载swiper,5版本为稳定版本 cnpm install swiper5 2.在组件中引入swiper包和对应样式,若多组件使用swiper,可以把swiper引入到main.js入口文件中: import swiper/css/swiper.css //引入swipe…...

Java书签 #使用MyBatis接入多数据源
楔子:当然,世上有很多优秀的女性,我也会被她们吸引。这对男人来说是理所当然的。但目光被吸引和内心被吸引是截然不同的。- 东野圭吾《黎明之街》 今日书签 在一些应用场景中,可能需要连接多个不同的数据库,例如连接不…...

神经网络基础-神经网络补充概念-23-神经网络的梯度下降法
概念 神经网络的梯度下降法是训练神经网络的核心优化算法之一。它通过调整神经网络的权重和偏差,以最小化损失函数,从而使神经网络能够逐渐逼近目标函数的最优值。 步骤 1损失函数(Loss Function): 首先,…...
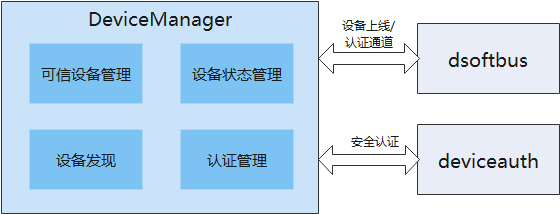
鸿蒙3.1 设备管理DeviceManager
介绍 DeviceManager组件在OpenHarmony上提供账号无关的分布式设备的认证组网能力,并为开发者提供了一套用于分布式设备间监听、发现和认证的接口。 其组成及依赖如下所示: 总结 设备管理模块其实就是软总线的包皮服务。目前权限都是控制系统uid,但是根据官方介绍,后续可…...

Git 目录详解
一、Git目录详解 在使用Git时,有几个目录和文件在Git项目中扮演着重要的角色,下面详细介绍一下这些目录和文件的作用 1、.git目录 .git目录是Git项目的核心,包含了Git的版本库和元数据等重要信息。在该目录中,有一些重要的子目录和…...
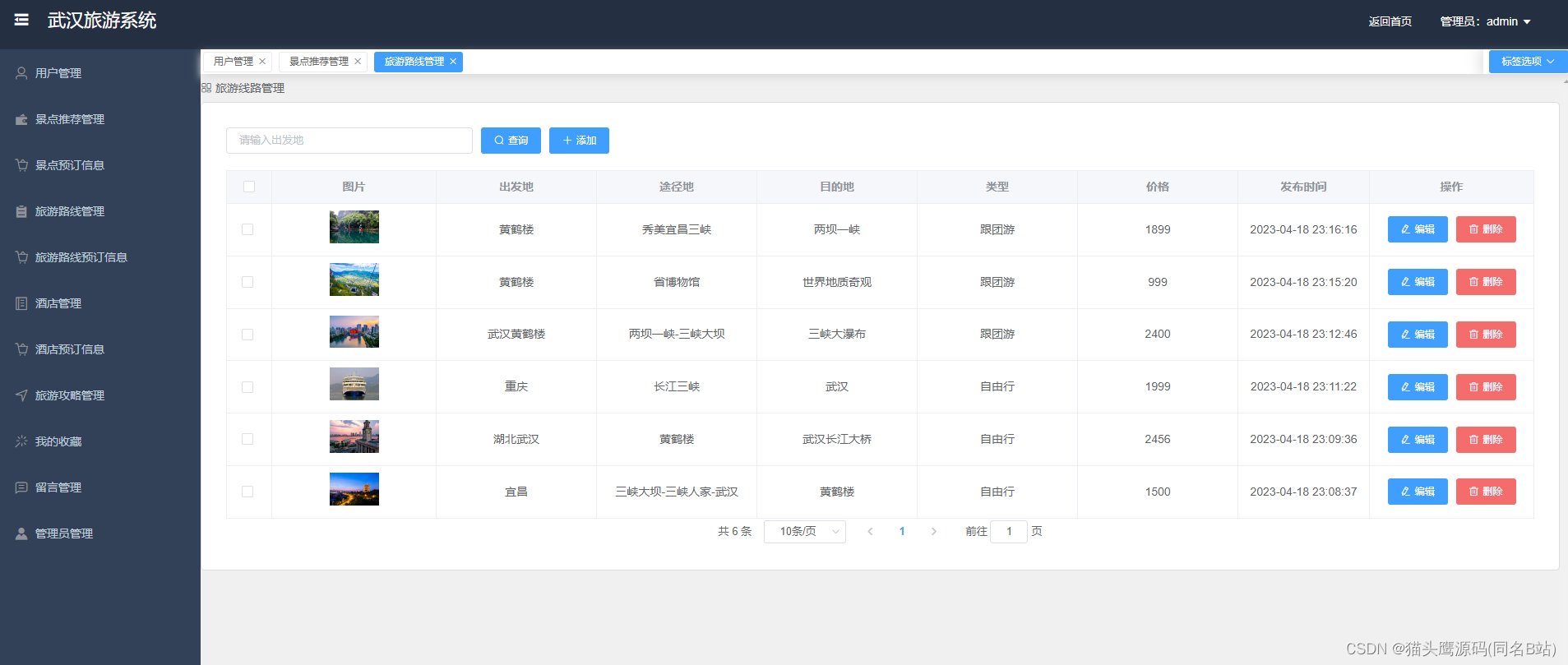
基于springboot+vue的武汉旅游网(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

步入React正殿 - React组件设计模式
目录 扩展学习资料 高阶组件 /src/components/hoc/withTooltip.js /src/components/hoc/itemA.jsx /src/components/hoc/itemB.jsx /src/App.js 函数作为子组件【Render pprops】 函数作为子组件 /src/components/rp/itemC.jsx【父组件】 /src/components/rp/withToo…...

Java 单例模式简单介绍
何为单例模式 所谓类的单例设计模式,就是采取一定的方法保证在整个的软件系统中,对某个类只能存在一个对象实例,并且该类只提供一个取得其对象实例的方法。 实现思路 如果我们要让类在一个虚拟机中只能产生一个对象,我们首先必…...

根据源码,模拟实现 RabbitMQ - 从需求分析到实现核心类(1)
目录 一、需求分析 1.1、对 Message Queue 的认识 1.2、消息队列核心概念 1.3、Broker Server 内部关键概念 1.4、Broker Server 核心 API (重点实现) 1.5、交换机类型 Direct 直接交换机 Fanout 扇出交换机 Topic 主题交换机 1.6、持久化 1.7…...

企业服务器数据库遭到malox勒索病毒攻击后如何解决,勒索病毒解密
网络技术的发展不仅为企业带来了更高的效率,还为企业带来信息安全威胁,其中较为常见的就是勒索病毒攻击。近期,我们公司收到很多企业的求助,企业的服务器数据库遭到了malox勒索病毒攻击,导致系统内部的许多重要数据被加…...
udp与can通信的选择与比较
UDP(用户数据报协议)和CAN(控制器局域网)是两种不同的通信协议,它们在实时传递性上有一些区别。 UDP是一种无连接的传输协议,它提供了简单的、不可靠的数据传输。UDP不提供可靠性保证、流控制或重传机制。…...

HoudiniVex笔记_P24_ForceBasics力基础
原视频:https://www.youtube.com/playlist?listPLzRzqTjuGIDhiXsP0hN3qBxAZ6lkVfGDI Bili:Houdini最强VEX算法教程 - VEX for Algorithmic Design_哔哩哔哩_bilibili Houdini版本:19.5 1、什么是Force 本章主要讲重力、弹力、速度与质量、…...
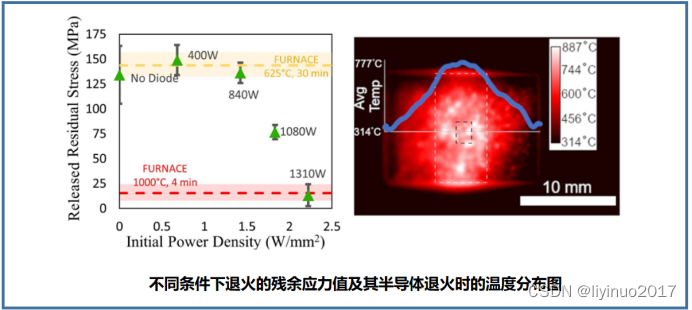
半导体退火那些事(1)
1.半导体退火的原理 半导体材料在晶体生长和制造过程中,由于各种原因会出现缺陷、杂质、位错等结构性缺陷,导致晶格不完整,施加电场后的电导率较低。通过退火处理,可以使材料得到修复,结晶体内部重新排列,…...
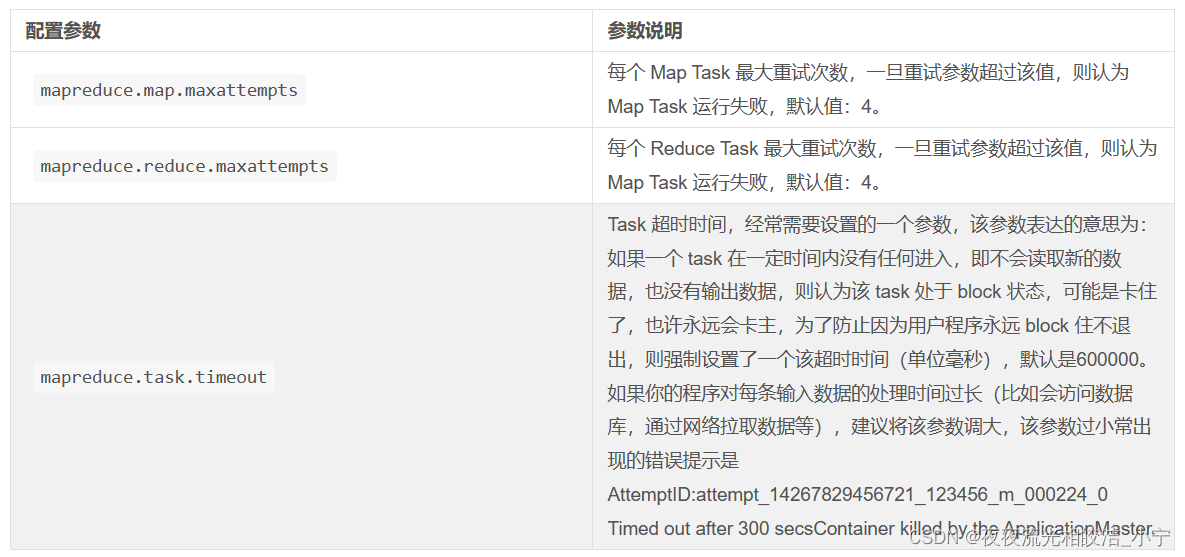
MapReduce介绍
目录 一、什么是MapReduce 二、MapReduce 的设计思想 2.1 分而治之 2.2 构建抽象模型:Map和Reduce 2.3 隐藏系统层细节 三、MapReduce 的框架原理 3.1 MRv1工作原理 3.1.1 MRv1架构工作原理图 3.1.1.1 流程说明 3.1.1.1.1 作业的提交 3.1.1.1.2 作业的初始化 3…...

Redis支持的主要数据结构操作命令有哪些?
Redis支持多种数据结构操作命令,包括以下主要命令: 字符串(Strings): SET:设置字符串键的值。GET:获取指定键的值。INCR/DECR:对存储整数的字符串执行加一或减一操作。APPEND&#x…...
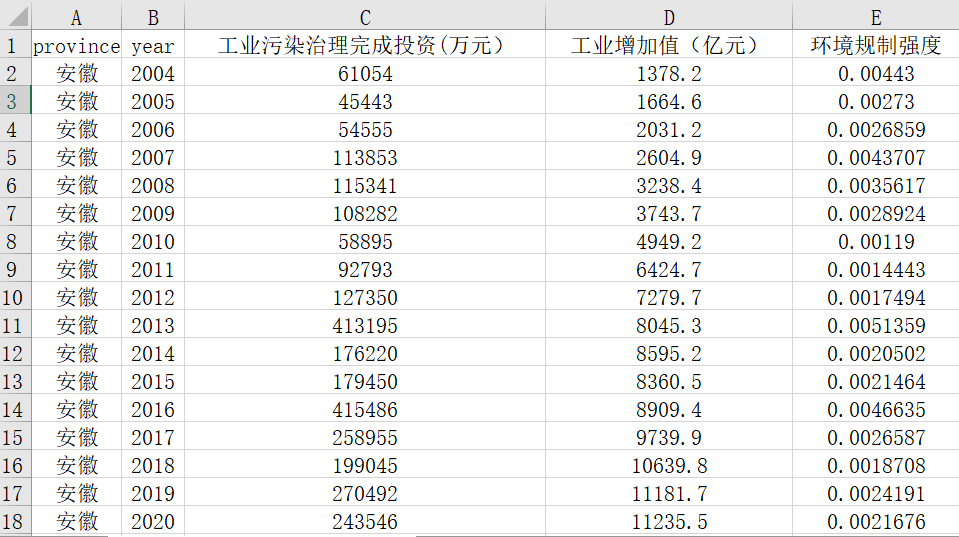
环境与能源创新专题:地级市绿色创新、碳排放与环境规制数据
数据简介:推动绿色发展,促进人与自然和谐共生是重大战略举措。绿色发展强调“绿水青山就是金山银山”,人与自然和谐共生重在正确处理生态环境保护与经济发展的关系。在着力于实现绿色发展的过程中,绿色创新是绿色发展的重要驱动因…...

设计模式之门面模式(Facade)的C++实现
1、门面模式提出 在组件的开发过程中,某些接口之间的依赖是比较紧密的,如果某个接口发生变化,其他的接口也会跟着发生变化,这样的代码违背了代码的设计原则。门面设计模式是在外部客户程序和系统程序之间添加了一层中间接口&…...
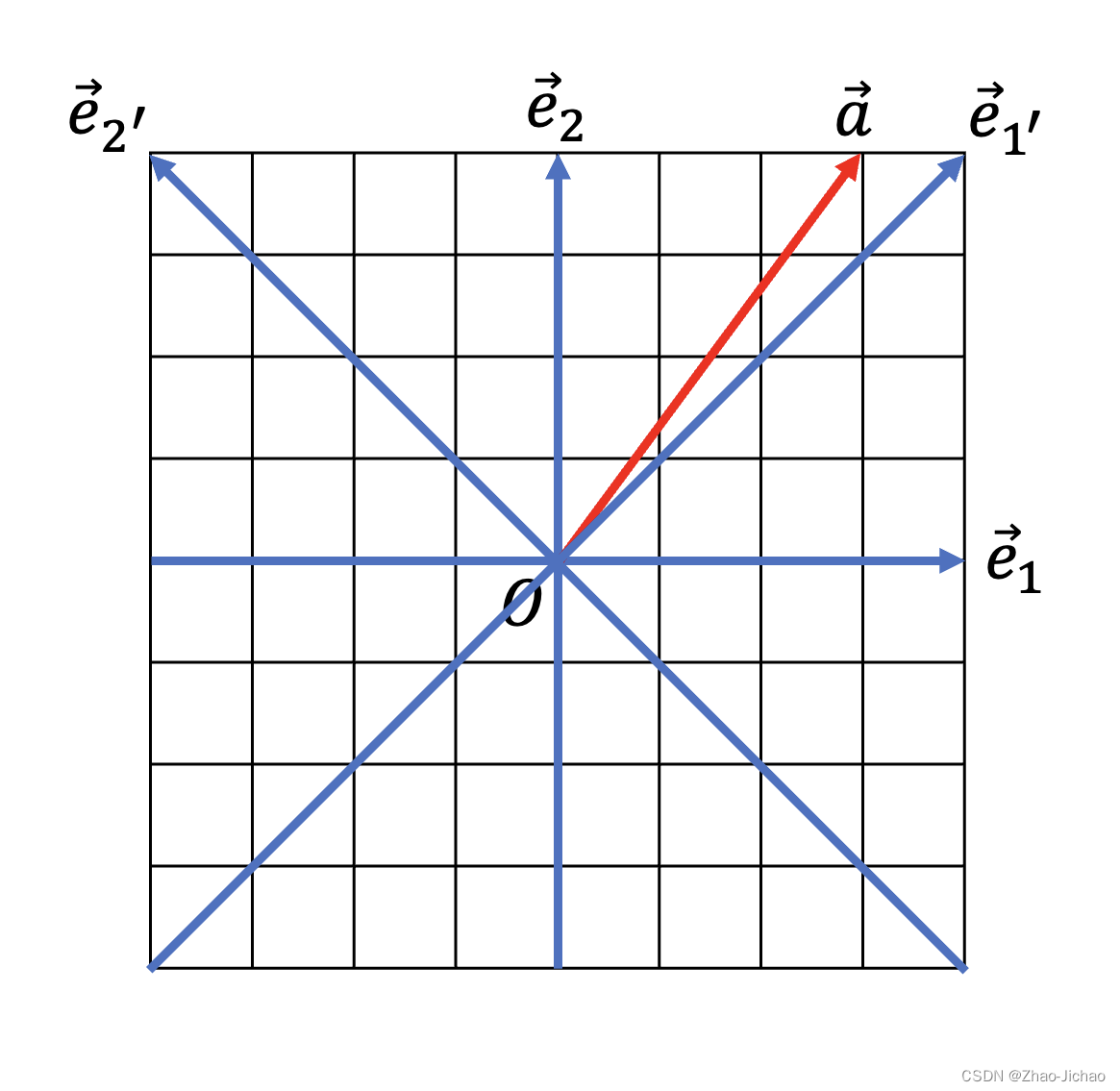
【数理知识】向量与基的内积,Matlab 代码验证
序号内容1【数理知识】向量的坐标基表示法,Matlab 代码验证2【数理知识】向量与基的内积,Matlab 代码验证 文章目录 1. 向量与基的内积2. 二维平面向量举例3. 代码验证Ref 1. 向量与基的内积 假设存在一个二维平面内的向量 a ⃗ \vec{a} a ,…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...
