leetcode 力扣刷题 两数/三数/四数之和 哈希表和双指针解题
两数/三数/四数之和 题目合集
- 哈希表求解
- 1. 两数之和
- 454. 四数相加Ⅱ
- 双指针求解
- 15.三数之和
- 18. 四数之和
这个博客是关于:找出数组中几个元素,使其之和等于题意给出的target 这一类题目的,但是各个题之间又有些差异,使得需要用不同的方法求解。 可以分为两类:一类是哈希表,一类是双指针。接下来详细讲解。
哈希表求解
首先,还是要明确,哈希表的主要用途是查找某个元素是否存在。
1. 两数之和
题目链接:1. 两数之和
题目内容:

根据题意就是在数组中找到两个元素使其和为target,最终返回的是下标。 我20年做这题的时候只会暴力求解,两层循环遍历所有可能的nums[i]+nums[j],看题解的哈希表云里雾里。 这次在哈希表的题目列表里看到这道题很震惊hhhhhh,竟然能看懂题解了呢……欣慰(捂脸哭)。
分析两层循环的目的:第一层循环遍历nums[i],第二次循环寻找nums[j] ,nums[i] + nums[j] =target,换个思路实际上是在下标i+1~n-1这个范围内查找是否存在target - nums[i],所以?可以考虑用哈希表来高效的查找。
这里再转换一下,实际上先初始化 j = 1,然后在 0~j-1这个范围内查找是否存在target - nums[j]实现起来更容易。因为随着j的增加,0~j-1这个范围越来越大,构造的哈希表越来越大,比较合理。
用什么实现哈希表呢? 题意要求返回下标,如果直接用unordered_set只能存数组元素值value,不能同时存下标index,因此用unordered_map,数组元素作key,下标作value(因为按照元素值来查找的)。代码实现如下(C++):
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {unordered_map<int,int> my_map; //map用来存没有匹配的元素及其下标//遍历numsfor(int i = 0; i < nums.size(); i++){//如果0~i-1中存在元素与nums[i]之和满足要求,直接返回if(my_map.count(target - nums[i])){//map[key]里面存的就是对应的下标return {my_map[target - nums[i]], i};}else{ //如果0~i-1中没有需要的元素,将nums[i]添加到map中//因为当前的nums[i']可能与后面(i向后移动后)nums[i]相加满足条件my_map[nums[i]] = i; }}return {};}
};
454. 四数相加Ⅱ
题目链接:454. 四数相加Ⅱ
题目内容:
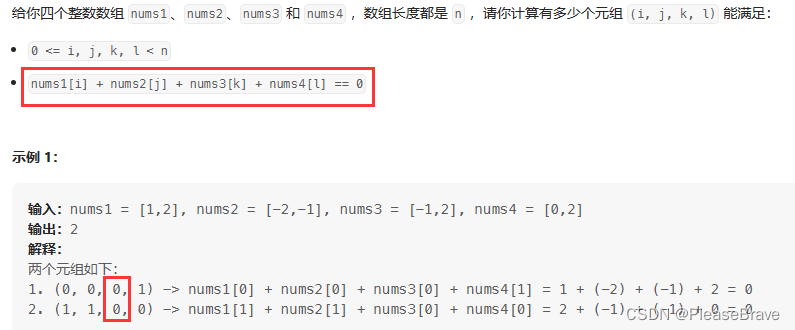
根据题目内容的描述,以及观察示例1,实际上题目就是在四个数组中,分别找一个元素,使得和=0。本题也没有强调元素不能重复出现,比如最极端的例子:

所以!实际上按照暴力求解的思路,四层循环遍历四个数组,找到所有可能的nums1[i] + nums2[j] + nums3[k] + nums4[p] ==0的(i,j,k,p)就好了【最终只需要返回次数】。但是暴力求解时间复杂度O(n^4)。怎么降低呢? x+y+z+m=0,那么任意选两个数之和,与剩下两个数的和互为相反数的,x+z= -(y+m)。因此可以考虑:
- 先遍历nums1和nums2得到所有可以的sum=nums1[i]+nums2[j],并以sum值为key,sum出现的次数为value,存为哈希表(unordered_map实现);
- 再遍历nums3和nums4,查找map中是否存在 -(nums3[k]+nums4[p]),如果存在就找到了满足条件的四元组,并且map[-(nums3[k]+nums4[p])]等于几,就找到了几个这样的四元组;
代码实现(C++):
class Solution {
public:int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {//key是sum=nums1[i]+nums2[j] value是能相加得到这个sum的次数unordered_map<int,int> sum;int ans = 0;//先遍历nums1和nums2for(int i = 0; i < nums1.size(); i++)for(int j = 0; j < nums2.size(); j++){sum[nums1[i] + nums2[j]]++;}//再遍历nums3和nums4for(int i = 0; i < nums3.size(); i++)for(int j = 0; j < nums4.size(); j++){//查找是否有满足条件的四元组if(sum.count(0 - nums3[i] - nums4[j]))ans+= sum[0 - nums3[i] - nums4[j]];}return ans;}
};
注意,nums1、nums2、nums3和nums4可以随便组合,上面代码是先遍历nums1和nums2,实际上可以先遍历nums2+nums4等等等,随便选两个数组先遍历,再遍历剩下两个数组。
双指针求解
接下来的题目,解题思路是先排序,再利用双指针。 重点在于,返回的满足条件的元组不能重复。这里的不能重复就面临着需要去重。
15.三数之和
题目链接:15. 三数之和
题目内容: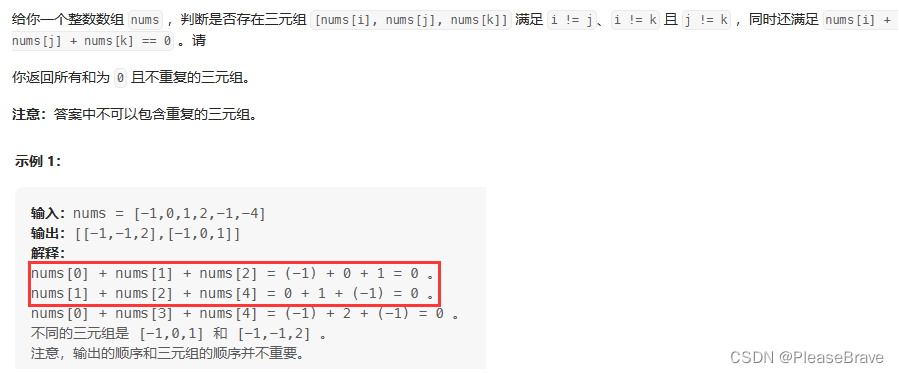
题目的重点在于返回的三元组不能重复。示例①中出现了[-1,0,1]和[0,1,-1】这样的就算重复,那么可以想到,如果先排序,去重很方便,只需要判断nums[i]和nums[i-1]的关系(相等和不相等)。【能够排序是因为最终返回的是nums[i]组成的三元组,而不是对应的下标;如果是下标的话,排序后元素下标就变化了,比如上面的两数之和就不能先排序,因为它要求返回下标。】
排序后,遍历nums元素,用i控制,同时使用left和right两个双指针,过程如下:
- left = i + 1,right = nums.size() -1;因为已经先排序了,如果nums[i] + nums[left] + nums[right] < 0,那就移动left(left++),向后寻找更大的数;
- 如果nums[i] + nums[left] + nums[right] > 0,那就移动right (right- -),向前寻找更小的数;
- 如果nums[i] + nums[left] + nums[right] = 0,就找到了这样的三元组,向结果数组中添加;
存在的问题: - 如果nums[i]已经大于0了,left和right都在nums后面,是≥nums[i]的,三个元素之和只会更大,后续是找不到nums[i] + nums[left] + nums[right] = 0的,因此当nums[i]>0时,不再往后遍历nums的元素;
- 如何去重呢?当nums[i]等于nums[i-1]时,后续找到的满足条件的nums[left]和nums[right],也必然和nums[i-1]那一轮找到的结果重合。因为不能重复,因此时没有必要的。
代码实现(C++):
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> ans;sort(nums.begin(), nums.end()); //先排序for(int i = 0; i < nums.size() - 2 ; i++){ //最外层 用i控制 遍历numsif(nums[i] > 0) break; //如果nums[i]>0,后续不可能找到结果,直接跳出循环//三元组第一个元素的去重if(i > 0 && nums[i] == nums[i-1]){continue;}//初始化双指针 int left = i + 1, right = nums.size() - 1;while(left < right){//满足条件,向结果数组中添加元素if(nums[i] + nums[left] + nums[right] == 0){ans.emplace_back(vector<int>{nums[i], nums[left], nums[right]});//三元组第二个元素去重,跳到不等于当前元素的下标处do{left++;}while(left < right && nums[left] == nums[left - 1]);//三元组第三个元素去重,跳到不等于当前元素的下标处do{right--;}while(left < right && nums[right] == nums[right + 1]);}else{//更小时移动leftif(nums[i] + nums[left] + nums[right] < 0){//如果当前元素不满足,和当前元素重复的那些值可以直接跳过do{left++;}while(left < right && nums[left] == nums[left - 1]);}else {//更大时移动right,并跳过和当前元素相等的元素do{right--;}while(left < right && nums[right] == nums[right + 1]); }}}}return ans; }
};
时间复杂度从三层循环的O(n^3)变成了一层遍历+一层双指针O(n^2)。
18. 四数之和
题目链接:14. 四数之和
题目内容:

这题目说得越来越看不懂,但实际上,就是从上一题三数之和变成了找四个数之后;固定的等于0,变成了等于target。同样时要求不重复,并且返回元素值组成的数组而不是下标。 因此套用三数之和的解题思路,先排序+双指针。不同点:
- 外层需要两层循环,里面一层用双指针遍历。
- 之前nums[i] > 0,就能跳出循环。但是本题nums[i] > target不能跳出循环,因为如果nums[i]是-4,target是-6,但是nums[i+1]=-2,这样后续也是可能找到四个元素之和等于-6的。因此只有在target>=0的情况下,nums[i] > target了,已经排序了那么nums[i]之后元素都大于0,相加会越来越大,找不到相加等于target的。
代码实现(C++):
class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> ans;sort(nums.begin(), nums.end());//先排序if(nums.size() < 4) return {}; //题意中n>=1,如果长度小于4直接返回空//最外层循环for(int i = 0; i <nums.size() - 3; i++){//提前结束 注意target>=0if(nums[i] > target && target >=0 ){break;}//一级去重if(i > 0 && nums[i] == nums[i-1]){continue;}//第二层循环 j控制for(int j = i + 1; j < nums.size() - 2; j++){//第一层没有跳出,但是第二层可加上nums[j]后可能跳出,同样注意需要target>=0才行if(nums[i] + nums[j] > target && target >= 0)break;//二级去重if(j > i + 1 && nums[j] == nums[j-1])continue;//双指针循环int left = j + 1, right = nums.size() -1;while(left < right){//找到满足条件的……操作同三数之和//注意题目中nums[i]是在[-10^9,10^9],这里不换成long,有测试样例不通过……真的离谱if(long(nums[i]) + long(nums[j]) + long(nums[left]) + long(nums[right]) == long(target)){ans.emplace_back(vector<int>{nums[i], nums[j], nums[left], nums[right]});do{left++;}while(left < right && nums[left] == nums[left - 1]);//跳过相同元素,第三个元素的去重do{right--;}while(left < right && nums[right] == nums[right + 1]);//跳过相同元素,第四个元素的去重}else{//如果大了移动rightif(long(nums[i]) + long(nums[j]) + long(nums[left]) + long(nums[right]) > long(target)){do{right--;}while(left < right && nums[right] == nums[right + 1]);}else{//如果小了移动leftdo{left++;} while(left < right && nums[left] == nums[left - 1]);}}}}}return ans;}
};
相关文章:

leetcode 力扣刷题 两数/三数/四数之和 哈希表和双指针解题
两数/三数/四数之和 题目合集 哈希表求解1. 两数之和454. 四数相加Ⅱ 双指针求解15.三数之和18. 四数之和 这个博客是关于:找出数组中几个元素,使其之和等于题意给出的target 这一类题目的,但是各个题之间又有些差异,使得需要用不…...
(搜索) 剑指 Offer 12. 矩阵中的路径 ——【Leetcode每日一题】
❓剑指 Offer 12. 矩阵中的路径 难度:中等 给定一个 m * n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。 单词必须按照字母顺序,通过相邻的单元格内的字母构…...
构建高可用的去中心化微服务集群架构指南
随着云计算、大数据和物联网的快速发展,企业对于可扩展的、高性能的微服务架构的需求也日益增长。传统的集中式架构已经不能满足这些需求,因此出现了去中心化的微服务集群架构。本文将介绍如何构建高可用的去中心化微服务集群架构,以满足企业…...

Sui主网升级至V1.7.1版本
Sui主网现已升级至V1.7.1版本,此升级包含了多项修复和优化。升级要点如下所示: #12915 协议版本提升至20版本。 在Sui框架中新增Kiosk Extensions API和一个新的sui::kiosk_extension模块。 您可以使用该API构建自定义的Kiosk应用程序,以…...
-[基础知识])
自然语言处理从入门到应用——LangChain:索引(Indexes)-[基础知识]
分类目录:《自然语言处理从入门到应用》总目录 索引(Indexes)是指为了使LLM与文档更好地进行交互而对其进行结构化的方式。在链中,索引最常用于“检索”步骤中,该步骤指的是根据用户的查询返回最相关的文档:…...
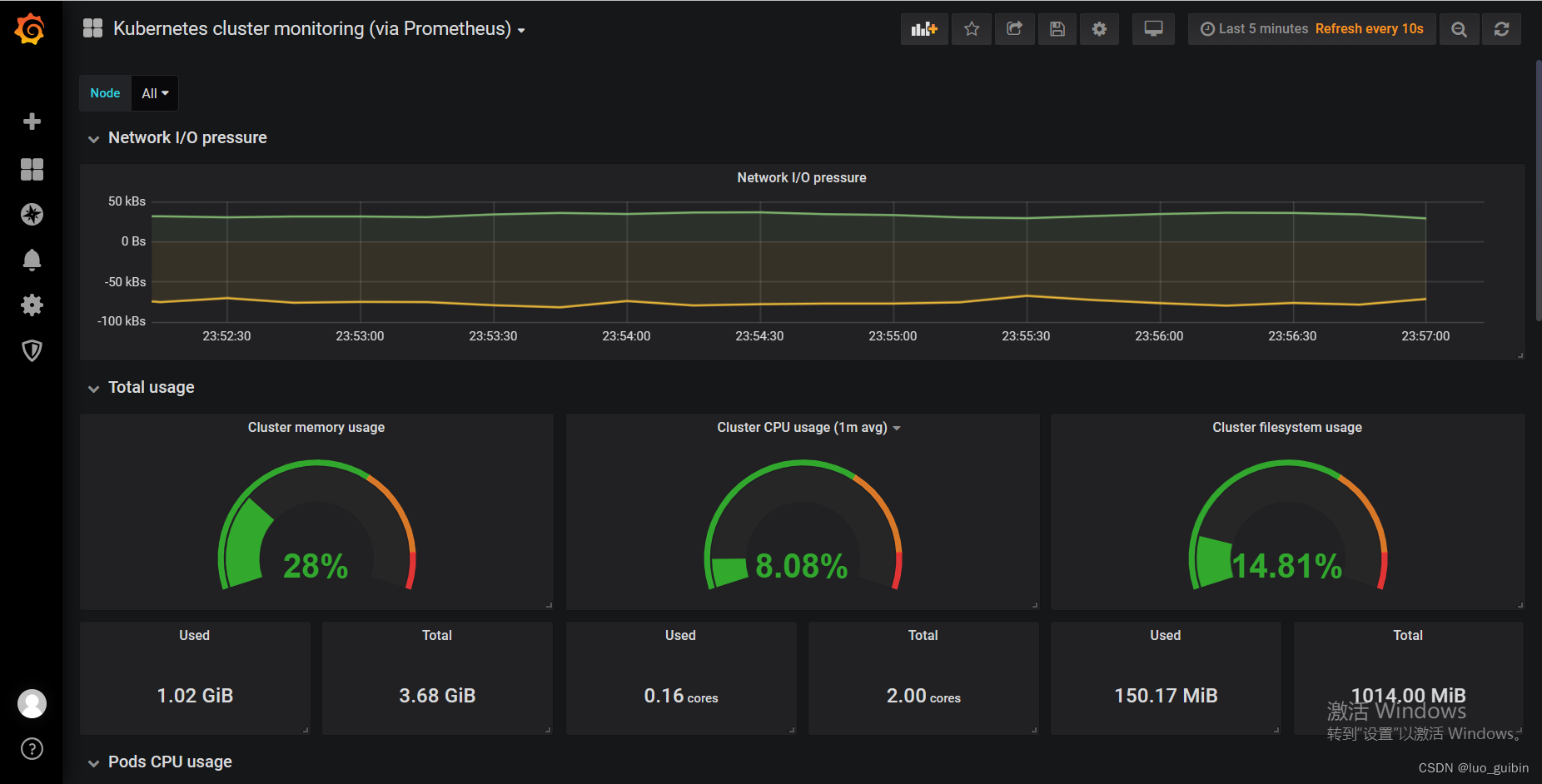
k8s集群监控方案--node-exporter+prometheus+grafana
目录 前置条件 一、下载yaml文件 二、部署yaml各个组件 2.1 node-exporter.yaml 2.2 Prometheus 2.3 grafana 2.4访问测试 三、grafana初始化 3.1加载数据源 3.2导入模板 四、helm方式部署 前置条件 安装好k8s集群(几个节点都可以,本人为了方便实验k8s集…...
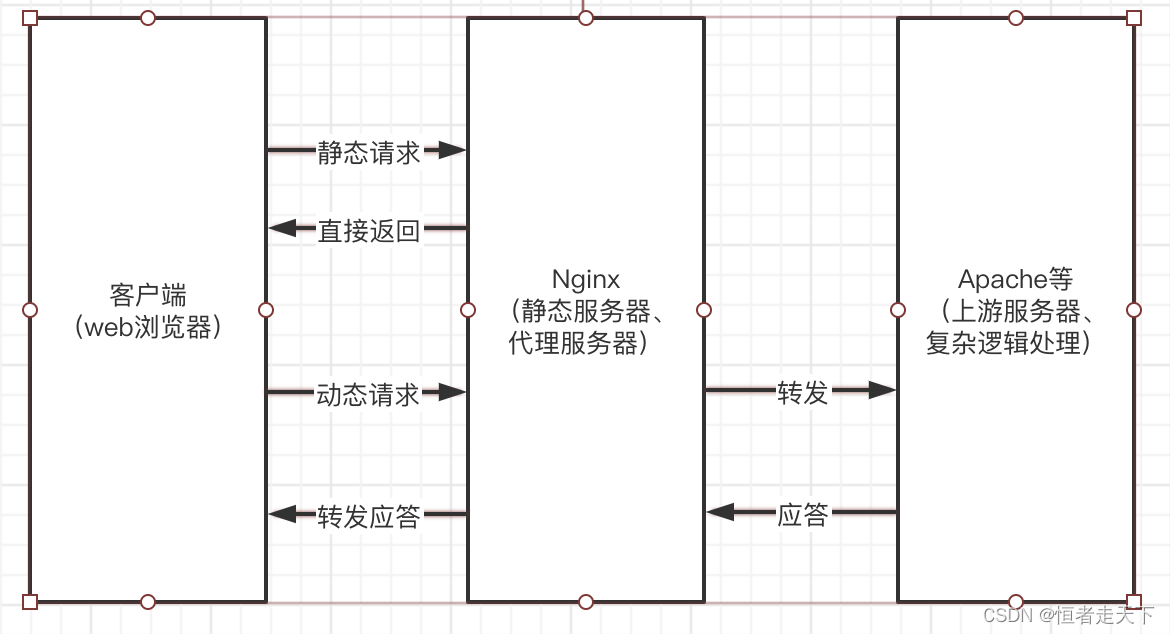
nginx反向代理流程
一、nginx反向代理流程 反向代理:使用代理服务器来接受internet上的连接请求,然后将请求转发给内部网络中的上游服务器,并将上游服务器得到的结果返回给请求连接的客户端,代理服务器对外表现就是一个web服务器。Nginx就经常拿来做…...

Java“牵手”根据店铺ID获取淘宝店铺所有商品数据方法,淘宝API实现批量店铺商品数据抓取示例
淘宝天猫商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取淘宝整店所有商品详情页面评价内容数据,您可以通过开放平台的接口或者直接访问淘宝商城的网页来获取店铺所有商品详情信息内的评论数据…...

从0开始yolov8模型目标检测训练
从0开始yolov8模型目标检测训练 1 大环境 首先有大环境,即已经准备好了python、nvidia驱动、cuda、cudnn等。 2 yolov8的虚拟环境 2.1 创建虚拟环境 conda create -n yolov8 python3.102.2 激活虚拟环境 注意:激活虚拟环境的时候,需要清…...

设计模式-抽象工厂模式
抽象工厂模式:该模式是对工厂模式的拓展,因为工厂模式中创建的产品都需要继承自同一个父类或接口,创建的产品类型相同,无法创建其他类型产品,所以抽象工厂模式对其进行拓展,使其可以创建其他类型的产品。 …...
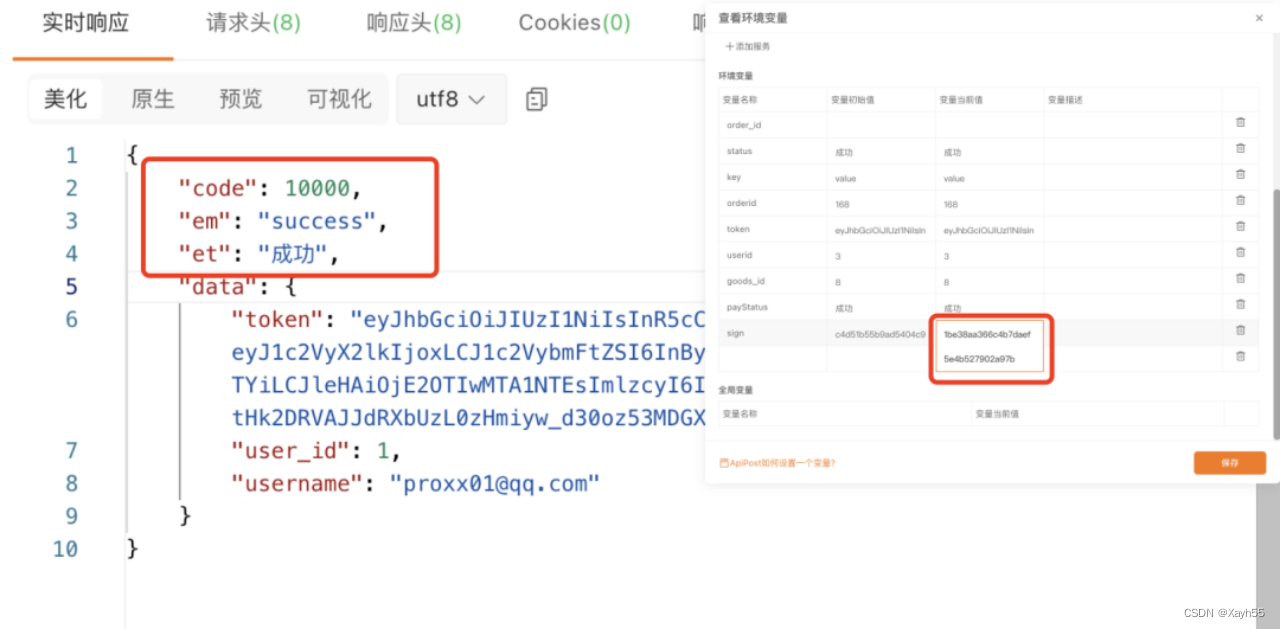
如何用Apipost实现sign签名?
我们平常对外的接口都会用到sign签名,对不同的用户提供不同的apikey ,这样可以提高接口请求的安全性,避免被人抓包后乱请求。 如何用Apipost实现sign签名? 可以在Apipost中通过预执行脚本调用内置的JS库去实现预执行脚本是在发送请求之前自…...
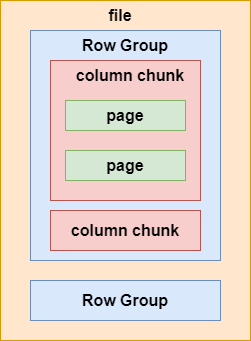
Hive底层数据存储格式
前言 在大数据领域,Hive是一种常用的数据仓库工具,用于管理和处理大规模数据集。Hive底层支持多种数据存储格式,这些格式对于数据存储、查询性能和压缩效率等方面有不同的优缺点。本文将介绍Hive底层的三种主要数据存储格式:文本文件格式、Parquet格式和ORC格式。 一、三…...
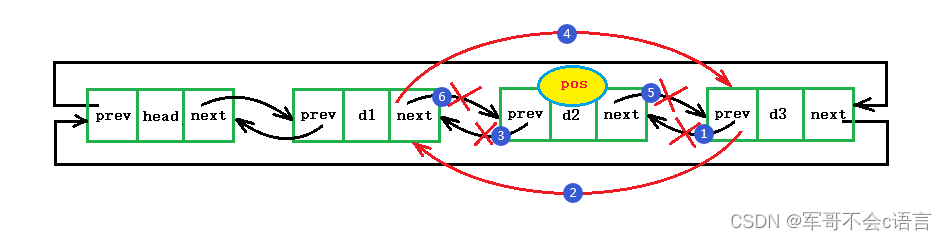
双向-->带头-->循环链表
目录 一、双向带头循环链表概述 1.什么是双向带头循环链表 2.双向带头循环链表的优势 3.双向带头循环链表简图 二、双向带头循环链表的增删查改图解及代码实现 1.双向带头循环链表的头插 2.双向带头循环链表的尾插 3.双向带头循环链表的头删 4.双向带头循环链表的尾删…...

Opencv4基于C++基础入门笔记:OpenCV环境配置搭建
文章目录: 一:软件安装 二:配置环境(配置完之后重启一下软件) 1.配置电脑系统环境变量 vs2012及其以下 vs2014及其以上 2.配置VS软件环境变量 vs2012及其以下 vs2014及其以上 三:测试 vs2012及其…...

JS基础之实现map方法
提示:内容虽少,但是里面也有好几个知识点。 step 1:实现函数 function mapTmp (fn){if(!Array.isArray(this) || !this?.length) return [];const arr [];this.forEach((item, index) > {const newItem fn(item, index, this);arr.pu…...
FPGA应用学习笔记-----复位电路(二)和小结
不可复位触发器若和可复位触发器混合写的话,不可复位触发器是由可复位触发器馈电的。 不应该出现的复位,因为延时导致了冒险,异步复位存在静态冒险 附加素隐含项,利用数电方法,消除静态冒险 这样多时钟区域还是算异步的…...
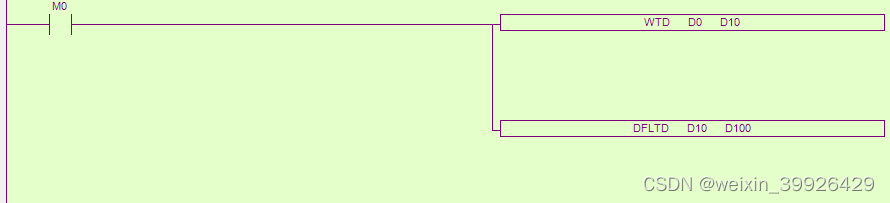
信捷 XD PLC 16位整数转换为双精度浮点数
完成16位整数转换为双精度浮点数,信捷XD PLC需要两个指令,逐步转换,一个指令搞不定。 具体的: 第1步:int16->int32 第2步:int32->Double 例子,比如说将D0转换成浮点数放到D100~D103...
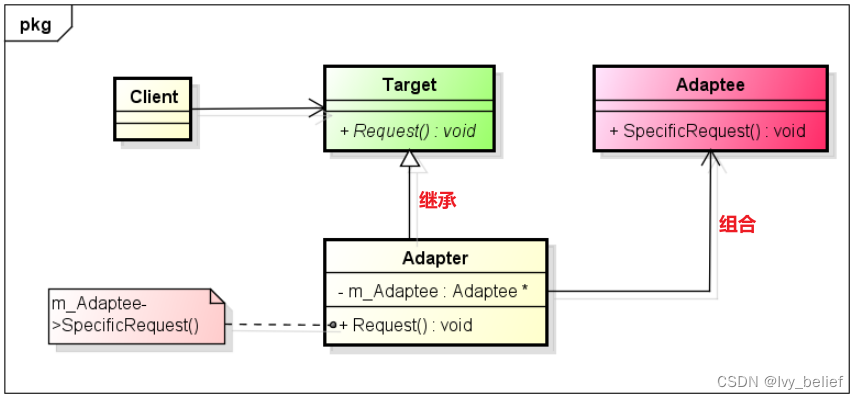
(二)结构型模式:1、适配器模式(Adapter Pattern)(C++实现示例)
目录 1、适配器模式(Adapter Pattern)含义 2、适配器模式应用场景 3、适配器模式的UML图学习 4、C实现适配器模式的示例 1、适配器模式(Adapter Pattern)含义 将一个接口转换为客户端所期待的接口,从而使两个接口…...
【编程二三事】ES究竟是个啥?
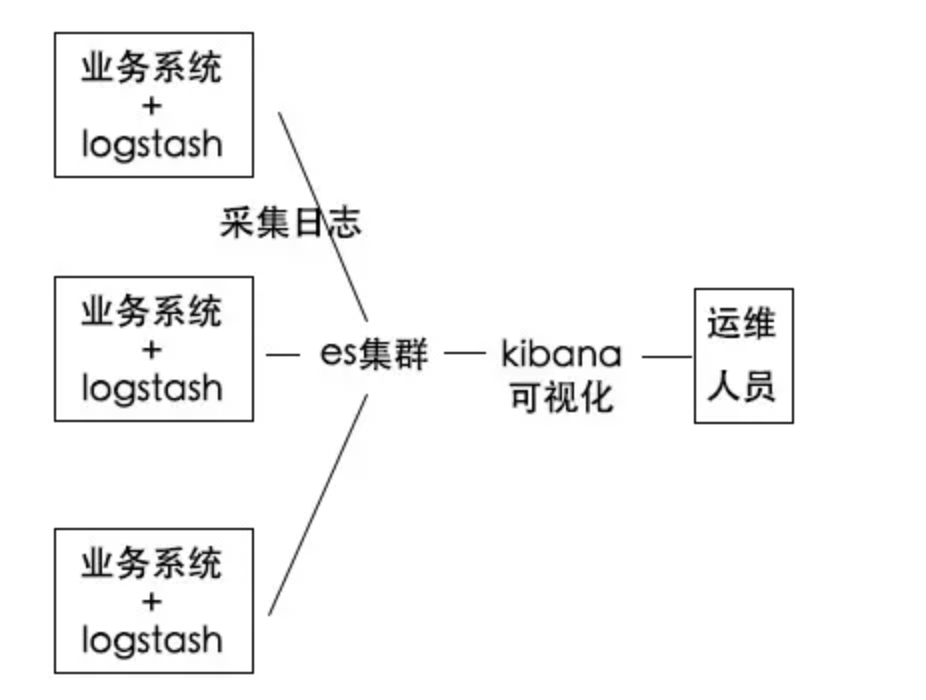
在最近的项目中,总是或多或少接触到了搜索的能力。而在这些项目之中,或多或少都离不开一个中间件 - ElasticSearch。 今天忙里偷闲,就来好好了解下这个中间件是用来干什么的。 ES是什么? ES全称ElasticSearch,是个基于Lucen…...
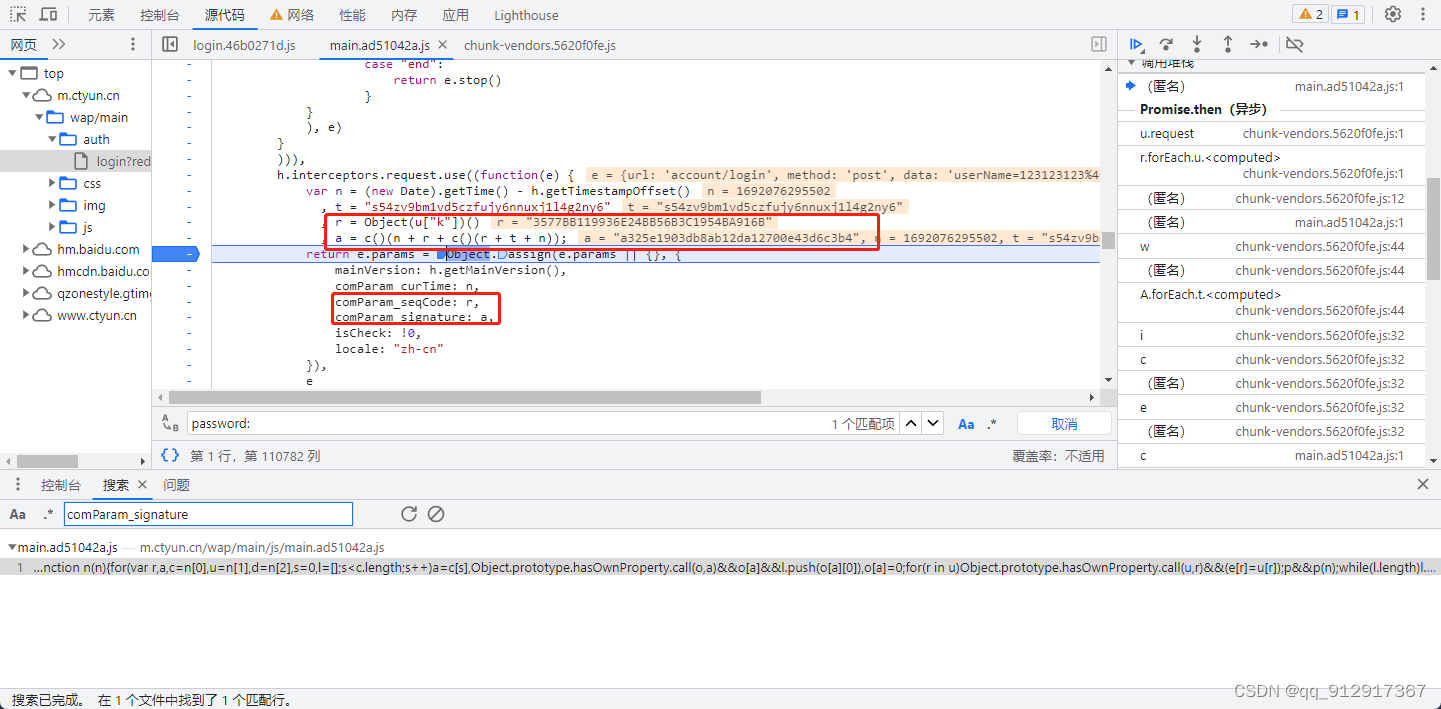
爬虫逆向实战(三)--天某云登录
一、数据接口分析 主页地址:天某云 1、抓包 通过抓包可以发现登录接口是account/login 2、判断是否有加密参数 请求参数是否加密? 通过“载荷”模块可以发现password、comParam_signature、comParam_seqCode是加密的 请求头是否加密? 无…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
