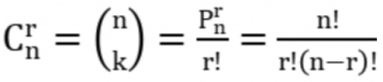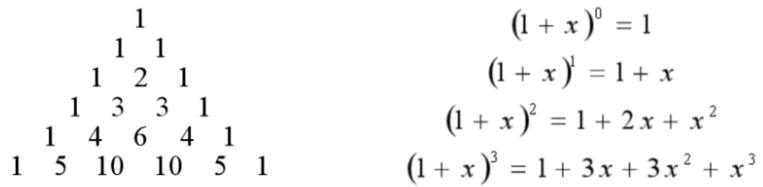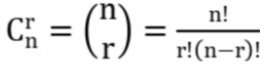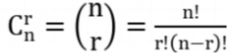组合数学原理与例题
目录
一、前言
二、计数原理
1、加法原理
2、分割立方体(lanqiaoOJ题号1620)
3、乘法原理
4、挑选子串(lanqiaoOJ题号1621)
5、糊涂人寄信(lanqiaoOJ题号1622)
6、战斗吧N皇后(lanqiaoOJ题号1623)
三、鸽巢原理
1、鸽巢原理概念
2、小蓝吃糖果(lanqiaoOJ题号1624)
四、二项式定理与杨辉三角
1、概念
2、杨辉三角形(2021年省赛,lanqiaoOJ题号1457)
一、前言
本文主要讲了计数原理、鸽巢原理、杨辉三角的概念与相关编程题。
二、计数原理
1、加法原理
- 加法原理:集合 S 被分成两两不相交的部分 S1、S2、S3、..、Sm,那么 S 的对象数目等于:|S| = |S1| + |S2| + |S3| + ... + |Sml
- 例:一个学生想学一门数学课,一门文化课,但不能同时选,现在从 4 门数学课和 4 门文化课中选,一共有 4+4=8 种方法选一门课。
- 加法原理的关键是将计数分解为若干个独立(不相容)的部分,保证既不重复也不遗漏地进行计数。
2、分割立方体(lanqiaoOJ题号1620)
【题目描述】
一个立方体,边长为 n,分割成 n×n×n 个单位立方体。任意两个单位立方体,或者有 2 个公共点,或者有 4 个公共点,或者没有公共点。请问,没有公共点和有 2 个公共点的立方体,共有多少对?
【输入描述】
一个整数n, 1<=n<=30
【思路】
反过来计算,先算出有 4 个公共点的立方体有多少对,然后用总对数减去。分几种情况讨论:
1) 正方体和周围 3 个正方体相邻,这种情况共有 8 个,就是顶角上的 8 个,总个数 3×8;
2) 正方体和周围 4 个正方体相邻,这种情况共有 (n-2)×12 个,总个数 4×(n-2)×12;
3) 正方体和周围 5 个正方体相邻,这种情况共有 6×(n×n-4×n+4) 个,总个数 5×6×(n×n-4×n+4);
4) 正方体和周围 6 个正方体相邻,这种情况共有 (n×n×n-n×n×6+n×12-8) 个,总个数 6×(n×n×n-n×n×6+n×12-8);
最后把这 4 个情况求和再除以 2。
正方体一共 n^3 个,共有 n^3(n^3-1)/2 种关系。
n=int(input())
if n==1:print(0) #边长为1时特判
else:sum=n*n*n*(n*n*n-1)//2 #总数edge3=8ans3=3*edge3edge4=(n-2)*12ans4=4*edge4edge5=n*n-4*n+4ans5=5*6*edge5edge6=n*n*n-n*n*6+n*12-8ans6=6*edge6print(sum-(ans3+ans4+ans5+ans6)//2)
3、乘法原理
- 令 S 是对象的有序对 (a,b) 的集合,其中第一个对象 a 来自大小为 p 的一个集合,对于对象 a 的每个选择,对象 b 有 q 个选择,那么 S 的大小:ISI-p×q
- 例:中性笔的长度有 3 种,颜色有 4 种,直径有 5 种。不同种类的中性笔有:3×4×5=60 种。
- 例:3^4×5^5×7^2×11^3的正整数因子有多少? 答: 这是算数基本定理的概念。3 有 0-4 这 5 种选择,5 有 6 个选择,7 有 3 个选择,11 有 4 个选择,因子总数是 5×6×3×4=360 种。
【排列数】
排列是有序的。
- 不可重复排列数:从 n 个不同的物品中取出 r 个,排列数为:
- P(n, r) = n(n- 1)(n - 2)...(n-r+1) = n!/(n-r)!
- 可重复排列数,从 n 个不同的物品中可重复地取出 r 个的排列数为:n^r
【组合数】
排列是有序的,组合是无序的。如果 S 中的元素都不相同,组合数:
4、挑选子串(lanqiaoOJ题号1621)
【题目描述】
有 n 个数,和一个整数 n。从这 n 个数选出一个连续子串,要求这个子串里面有 k 个数要大于等于 m。问一共能选出多少个子串。显然子串个数要大于等于 k 个。
【输入描述】
第一行是 3 个整数 n、m、k。第二行是 n 个整数 a1、a2、...、an,表示序列。2<=n<=200000,1<=k<=n/2,1<=m, ai<=10^9
【输出描述】
输出一个整数表示答案。
【思路】
一个个地输入 ai,直到输入的数字里,大于 m 的数够 k 个,就可以开始统计了。
1)若正好到 k 个数,情况总数是:第一个大于 m 的位置 i(之前),乘以 i(当前) 以后的个数,相当于求出了这一段区间的总个数。
2)大于 k 个后,怎么求出以后的序列个数而且保证不重复呢?从前往后推理,用倒数第二个位置-倒数第一个位置的差,乘上后面的个数。(这句话需要自己琢磨一下,讲得并不清晰,最好能举一个具体的例子来说明一下)
n,m,k=map(int,input().split())
a=[0]+list(map(int,input().split()))
sum=0
d=[0]*(n+1)
t=0
for i in range(n+1):if a[i]>=m:t+=1d[++t]=i #d[]: 比m大的数字所在位置。这里的++没有任何意义,python并无自增和自减if t>=k: #首先统计出k个比m大的if t==k:sum+=d[1]*(n-i+1)else:sum+=(d[t-k+1]-d[t-k])*(n-i+1)
print(sum)
5、糊涂人寄信(lanqiaoOJ题号1622)
【题目描述】
有一个糊涂人,写了 n 封信和 n 个信封,到了邮寄的时候,把所有的信都装错了信封。求装错信封可能的种类数。
【输入描述】
每行输入一个正整数 n,表示一种情况。(n<20)
【输出描述】
输出相应的答案。
【思路】
题目建模为:有 1~n 个数字,分别放在 n 个位置,问都放错的情况有多少种。
用 DP 来做,定义 dp[],dp[i] 表示数字 1~i 都放错的种类数。dp[n] 是答案。
下面考虑状态转移方程,从 1~i 递推到 i。
数字 i 如果放错,有 i-1 个位置可以放,假设其放在第 k 个位置。对于数字 k,可以放在 i 位置也可以不放在 i 位置。
如果 k 放在 i 位置,那么对于剩下 i-2 个数字放的次数,就是 i-2 个数字都放错的方法数 dp[i-2]。
如果 k 不放在 i 位置,和 i-1 个数字放错的情况相同,为 dp[i-1]。
状态转移方程:dp[i] = (i-1)*(dp[i-1]+dp[i-2])
- 注意本题的输入:没有明确终止
- 第 6 行处理了这种情况。
import sys
def f(n):if n==0 or n==1:return 0elif n==2:return 1else:return (n-1)*(f(n-1)+f(n-2))
for n in sys.stdin: #读入n,和C++代码的while(cin>>n)功能一样n=int(n)print(f(n))
6、战斗吧N皇后(lanqiaoOJ题号1623)
【题目描述】
在一个 N*M 的棋盘中,存在多少种方式使得两个皇后可以互相攻击。
【输入】
输入有若干行,每行两个数 N,M (1<=N,M<=106)
【输出】
对于每组测试数据输出一行表示答案
【思路】
两个皇后如果能攻击,位于同一行、同一列、同一对角线。
设矩阵为 n*m,前 2 者的可能性是 (m+n-2)*n*m。(同一行:n*m*(m-1);同一列:m*n*(n-1))
其他情况请自己思考。(对角线情况)
注意本题的输入没有明确终止,且每行读取 2 个数。第 2~4 行处理了这种输入的情况。
import sys
for line in sys.stdin: #读多个数,和C++的while(cin>>n>>m)功能一样n=int(line.split()[0])m=int(line.split()[1])if n>m:n,m=m,nif n==1:print(m*(m-1))continueans=m*n*(m+n-2)ans+=2*(n-2)*(n-1)*(2*n-3)//3ans+=2*(m-n+1)*n*(n-1)print(ans)
三、鸽巢原理
1、鸽巢原理概念
鸽巢原理,又称抽屉原理。
鸽巢原理:把 n+1 个物体放进 n 个盒子,至少有一个盒子包含 2 个或更多的物体。
例:在370人中,至少有2人生日相同;
答:把365天看成365个抽屉。把365人放进365个抽屉,不管怎么放,抽屉里面都有人了。
例:n个人互相握手,一定有2个人握手次数相同
答:每人跟其他人握手,最少可以是 0 次,最多可以是 n-1 次。
如果握手最少的是 0 次,那么剩下的 n-1 人中,握手最多的人不会超过 n-2 次。0~n-2 共 n-1 种情况。
如果握手最少的张三是 1 次,那么剩下的 n-1 人中,握手最多的李四除了跟张三握手一次,跟其他 n-2 人最多握手 n-2 次,李四最多握手 n-1 次。1~n-1 共 n-1 种情况。
如果握手最少的张三是 2 次,那么剩下的 n-1 人中,握手最多的李四除了跟张三握手一次,跟其他 n-2 人最多握手 n-2 次,李四最多握手 n-1 次。
2~n-1 共 n-2 种情况。
所以握手次数最多有 n-1 种情况,最少只有 1 种情况。
把最多的 n-1 种情况看成 n-1 个抽屉,n 个人放进这 n-1 个抽屉,至少有一个抽屉里面有 2 人。
2、小蓝吃糖果(lanqiaoOJ题号1624)
【题目描述】
Gardon有 n 种糖果,每种数量已知。Gardon 不喜欢连续 2 次吃同样的糖果。问有没有可行的吃糖方案。
【输入】
第一行是整数 N,O<n<1000000,第二行是 n 个数,表示 n 种糖果的数量 mi,0<mi<1000000
【输出】
输出一行,包含一个 "Yes" 或 "no"。
【思路】
鸽巢原理,用 “隔板法” 求解。
找出最多的一种糖果,把它的数量 K 看成 K 个隔板,隔成 K 个空间(把每个隔板的右边看成一个空间);其它所有糖果的数量为 S。
最多的一种糖果,把它的数量 K 看成 K 个隔板,隔成 K 个空间 (把每个隔板的右边看成一个空间);其它所有糖果的数量为 S。
1)如果 S<K-1,把 S 个糖果放到隔板之间,这 K 个隔板不够放,必然至少有 2 个隔板之间没有糖果,由于这 2 个隔板是同一种糖果,所以无解。
2)S>=K-1时,肯定有解。其中一个解是:把 S 个糖果排成一个长队,其中同种类的糖果是挨在一起的,然后每次取 K 个糖果,按顺序一个一个地放进 K 个空间。由于隔板数量比每一种糖果的数量都多,所以不可能有 2 个同样的糖果被放进一个空间里。把 S 个糖果放完,就是一个解,一些隔板里面可能放好几种糖果。
n=int(input())
a=list(map(int,input().split()))
if sum(a)-max(a)<max(a)-1:print("No")
else:print("Yes")四、二项式定理与杨辉三角
1、概念
杨辉三角:排列成如下三角形的数字
每个数是它上面 2 个数的和。
求杨辉三角第 n 行的数字,可以模拟这个推导过程,逐级递推,复杂度 O(n^2)。用数学公式计算,可以直接得到结果,这个公式是 (1 +x)^n。
二项式系数就是 (1+x)^n 展开后第 r 项的系数。
理解:(1+x)^n 的第 r 项,就是从 n 个 x 中选出 r 个,这就是组合数的定义
当 n 较大,且需要取模时,二项式系数有两种计算方法:
1)递推公式:
公式是杨辉三角的定义,即 “每个数是它上面 2 个数的和” 。计算复杂度是 O(n^2)。
2)用逆直接计算因为输出取模,那么不用递推公式,直接用公式计算更快。不过,由于除法不能直接取模,需要用到逆。用逆计算二项式系数,有:
用逆计算二项式系数,复杂度是 O(n) 的。
2、杨辉三角形(2021年省赛,lanqiaoOJ题号1457)
【题目描述】
如果我们按从上到下、从左到右的顺序把杨辉三角形的所有数排成一列,可以得到如下数列:1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ...。给定一个正整数 N,请你输出数列中第一次出现 N 是在第几个数?
【输入描述】
输入一个整数 N。 N<=1000000000
【输出描述】
输出一个整数表示答案。
- 直接计算杨辉三角的每个数,然后推导出 N 的位置。上一行的 2 个数相加得下一行的一个数。例如上一行是 b[0]~b[k],下一行是 a[0]~a[k+1],那么 a[i] = b[i-1] + b[i]。
- 推算过程只用一个数组完成,和 DP 的自我滚动数组的原理一样,即 a[i] = a[i-1] + a[i]
def f():n=int(input())a=[0]*100050sum=0 #sum等于1~line行的数字个数line=0sum,a[0]=1,1if n==1:print(1)returnfor line in range(1,50000): #line: 杨辉三角的第line行for i in range(line,0,-1): #倒过来循环,和DP的自我滚动数组的原理一样a[i]=a[i-1]+a[i] #上一行的2个数相加得下一行的一个数if a[i]==n:print(sum+line-i+1)returnsum+=(line+1) #1~line行的数字个数。每行比上一行多一个,累加
f()
以上,组合数学原理与例题
祝好
相关文章:
组合数学原理与例题
目录 一、前言 二、计数原理 1、加法原理 2、分割立方体(lanqiaoOJ题号1620) 3、乘法原理 4、挑选子串(lanqiaoOJ题号1621) 5、糊涂人寄信(lanqiaoOJ题号1622) 6、战斗吧N皇后(lanqiaoO…...
【机器学习 深度学习】通俗讲解集成学习算法
目录:集成学习一、机器学习中的集成学习1.1 定义1.2 分类器(Classifier)1.2.1 决策树分类器1.2.2 朴素贝叶斯分类器1.2.3 AdaBoost算法1.2.4 支持向量机1.2.5 K近邻算法1.3 集成学习方法1.3.1 自助聚合(Bagging)1.3.2 提升法(Boosting)1.3.2.1 自适应adaboost1.3.3 …...

汉字----dgfont
Abstract 字符生成是一个具有挑战性的问题,特别是对于一些由大量字符组成的书写系统,近年来受到了广泛的关注。然而,现有的字体生成方法通常是在监督学习中。它们需要大量的配对数据,这是劳动密集型和昂贵的收集。此外,常见的图像到图像转换模型通常将风格定义为纹理和颜…...

C# chart绘图 鼠标响应
1、图形自动滚动设置 chart1.ChartAreas[0].AxisX.Maximum 横坐标显示区域最大值 chart1.ChartAreas[0].AxisX.Minimum 横坐标显示区域最小值 显示宽度 chart1.ChartAreas[0].AxisX.Maximum - chart1.ChartAreas[0].AxisX.Minimum chart1.ChartAreas[0].AxisX.Maximum x_d…...
结构体与引用
1.结构体基本概念结构体属于用户自定义的数据类型,允许用户存储不同的数据类型2.结构体定义和使用语法: struct 结构体 { 结构体成员列表 };通过结构体创建变量的方式有三种:struct 结构体名 变量名struct 结构体名 变量名 { 成员1值,成员2值...}定义结构…...

13.罗马数字转整数
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。字符 数值I 1V 5X 10L 50C 100D 500M 1000例如, 罗马数字 2 写做 II ,即为两个并列的 1 。12 写做 XII ,即为 X II 。 27 写做 XX…...

JVM垃圾回收机制
垃圾回收机制(GC) 内存管理 Java的内存管理很大程度指的就是对象的管理,其中包括对象空间的分配和释放。 对象空间的分配:使用new关键字创建对象即可 对象空间的释放:将对象赋值null即可。垃圾回收器将负责所有“不…...
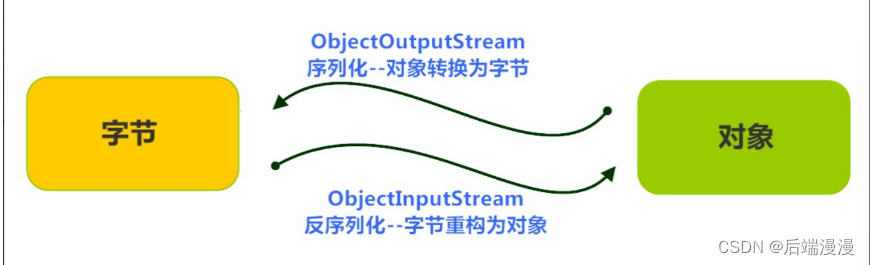
Java File类、IO流、Properties属性类
文章目录一、补充二、File类File类的含义创建多级文件File类的常见方法三、IO流IO流分类输入输出流FileOutputStreamInputStreamInputStream与OutputStream的实例ReaderWriterFileReader和FileWriter的实例缓冲流转换流序列化与ObjectInputStream、ObjectOutputStream打印流Pro…...

MySQL备份恢复(十二)
文章目录1. MySQL数据损坏类型1.1 物理损坏1.2 逻辑损坏2. DBA运维人员备份/恢复职责2.1 设计备份/容灾策略2.1.1 备份策略2.1.2 容灾策略2.2 定期的备份/容灾检查2.3 定期的故障恢复演练2.4 数据损坏时的快速准确恢复2.5 数据迁移工作3. MySQL常用备份工具3.1 逻辑备份方式3.2…...

【Java|golang】1792. 最大平均通过率---封装最小堆
一所学校里有一些班级,每个班级里有一些学生,现在每个班都会进行一场期末考试。给你一个二维数组 classes ,其中 classes[i] [passi, totali] ,表示你提前知道了第 i 个班级总共有 totali 个学生,其中只有 passi 个学…...

PHP 页面静态化
前言随着网站的内容的增多和用户访问量的增多,网站加载会越来越慢,受限于带宽和服务器同一时间的请求次数的限制,,我们往往需要在此时对我们的网站进行代码优化和服务器配置的优化。一、页面静态化概念静态化定义静态化就是指把原…...

【Python】进制、计算机中的单位、编码、数据类型、索引、字符串切片、字符串的功能方法
一、进制计算机中底层所有的数据都是以 010101 的形式存在(图片、文本、视频等)。二进制八进制十进制(也就是我们熟知的阿拉伯数字)十六进制进制转换v1 bin(25) # 十进制转换为二进制 print(v1) # "0b11001"v2 oct(23…...

基于android的无人健身房
需求信息: 1:客户登录:首次登陆必须注册,用户注册完成后可以进入软件查看自己的金额、会员等级、消费和健身时长。 2:计费功能:用户通过软件扫描二维码后即可进入健身房,软件显示欢迎进入健身房…...

带你Java基础入门
首先我们都知道的,Java是一种高级计算机语言,是可以编写跨平台应用软件、完全面向对象的程序设计语言。相对于零基础小白如何更加快速的入门java?小编给大家整理了java300集自学教程视频,非常适合零基础的小伙伴,一周时间实现快速…...
VNCTF 2023 - Web 象棋王子|电子木鱼|BabyGo Writeups
象棋王子 签到题,jsfuck解密 丢到console得到flag 电子木鱼 后面两道都是代码审计,这题是rust,题目给出了源码,下载下来看 关键代码: 由于限制,quantity只能为正数 功德也只能是正数(负数的…...
)
「JVM 编译优化」插入式注解处理器(自定义代码编译检查)
JDK 的编译子系统暴露给用户直接控制的功能相对很少,除了虚拟机即时编译的若干参数,便只有 JSR-296 中定义的插入式注解处理器 API; 文章目录1. 目标2. 实现3. 运行与测试4. 其他应用案例1. 目标 前端编译器在讲 Java 源码编译成字节码时对源…...

一文彻底理解大小端和位域 BIGENDIAN LITTLEENDIAN
一文彻底理解大小端和位域 为什么有大小端 人们一直认为大道至简,就好像物理学上的世界追求使用一个理论来统一所有的现象。为什么cpu存在大小端之分,一言以蔽之,这两种模式各有各的优点,其各自的优点就是对方的缺点,…...
面试准备知识点与总结——(虚拟机篇)
目录JVM的内存结构JVM哪些部分会发生内存溢出方法区、永久代、元空间三者之间的关系JVM内存参数JVM垃圾回收算法1.标记清除法2.标记整理3.标记复制说说GC和分代回收算法三色标记与并发漏标的问题垃圾回收器项目中什么时候会内存溢出,怎么解决类加载过程三个阶段何为…...
spring cloud 集成 seata 分布式事务
spring cloud 集成 seata 分布式事务 基于 seata-server 1.6.x 序言 下载 seata-server 准备一个数据库 seata 专门为 seata-server 做存储,如, 可以指定 branch_tabledistributed_lockglobal_tablelock_table 准备一个业务库,比如存放定单ÿ…...
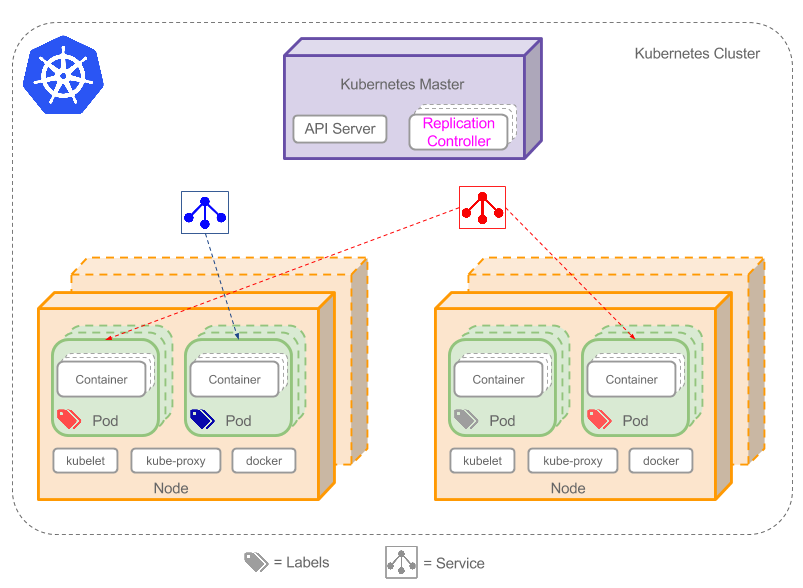
k8s篇之概念介绍
文章目录时光回溯什么是K8SK8S不是什么一、K8S构成组件控制平面组件(Control Plane Components)kube-apiserveretcdkube-schedulerkube-controller-managercloud-controller-managerNode 组件kubeletkube-proxy容器运行时(Container Runtime&…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...