工程监测振弦采集仪采集到的数据如何进行分析和处理
工程监测振弦采集仪采集到的数据如何进行分析和处理
振弦采集仪是一个用于测量和记录物体振动的设备。它通过测量物体表面的振动来提取振动信号数据,然后将其转换为数字信号,以便进行分析和处理。在实际应用中,振弦采集仪是广泛应用于机械、建筑、航空航天和汽车等领域的仪器之一。本文将从数据采集和准备、数据分析和处理以及数据可视化三个方面来介绍振弦采集仪采集到的数据分析和处理方法。

一、数据采集和准备
在进行数据分析和处理前,首先需要进行数据采集和准备。数据采集需要严格遵守采集仪器的使用说明,以保证采集到的数据的准确性和可信度。同时,需要根据实际情况设置采集参数,包括采样频率、采样时间等。在采集数据时,应保持环境安静,以避免外界干扰。
采集到数据后,需要进行数据清洗和处理。处理数据前,需要先将采集到的数据转换为数字信号文件。对于振弦采集仪,常见的文件格式有CSV、Excel等。

二、数据分析和处理
数据分析和处理主要包括特征提取、频谱分析和时频分析等。
1. 特征提取
特征提取是将采集到的数据转换为有意义的信息,以便更好地理解数据。常见的特征包括振幅、峰值、最大、最小值等。
2. 频谱分析
频谱分析是将时间域信号转换为频域信号,以便更好地分析信号的频率特征。频谱分析常见的方法有傅里叶变换、小波变换、短时傅里叶变换等。其中,傅里叶变换是最基本的频谱分析方法之一。在MATLAB中,可以使用fft函数进行傅里叶变换,然后将结果转换为幅度谱和相位谱。
3. 时频分析
时频分析是将信号在时域和频域上分析,以便更好地揭示信号的时频特性。常见的时频分析方法有短时傅里叶变换、小波包分析等。
三、数据可视化
数据可视化是将分析和处理后的数据呈现为可视化图表或图形,以便更好地理解数据。

振弦采集仪采集到的数据需要进行数据采集和准备、数据分析和处理以及数据可视化等过程。通过这些过程,可以更好地理解和分析振动数据,并为后续研究和应用提供支持。
相关文章:

工程监测振弦采集仪采集到的数据如何进行分析和处理
工程监测振弦采集仪采集到的数据如何进行分析和处理 振弦采集仪是一个用于测量和记录物体振动的设备。它通过测量物体表面的振动来提取振动信号数据,然后将其转换为数字信号,以便进行分析和处理。在实际应用中,振弦采集仪是广泛应用于机械、建…...
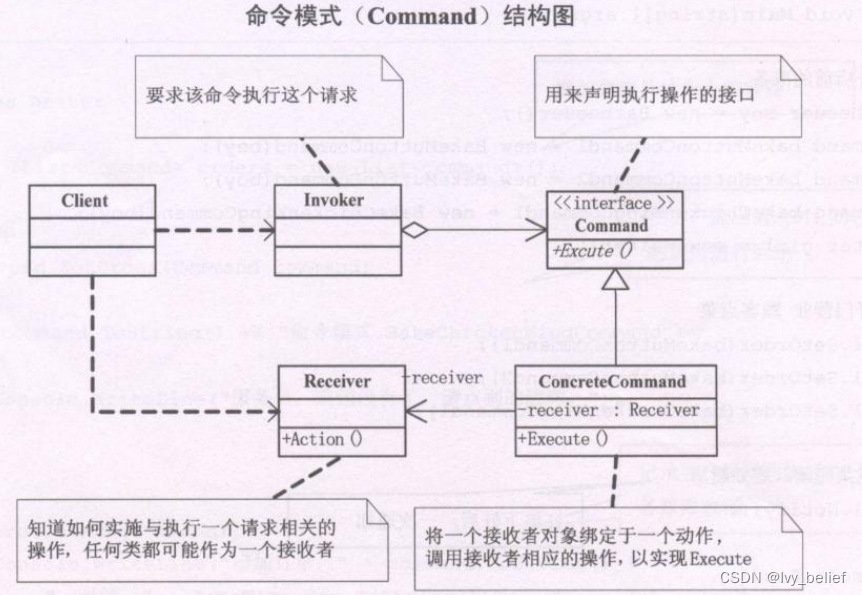
(三)行为模式:2、命令模式(Command Pattern)(C++示例)
目录 1、命令模式(Command Pattern)含义 2、命令模式的UML图学习 3、命令模式的应用场景 4、命令模式的优缺点 5、C实现命令模式的实例 1、命令模式(Command Pattern)含义 命令模式(Command)ÿ…...
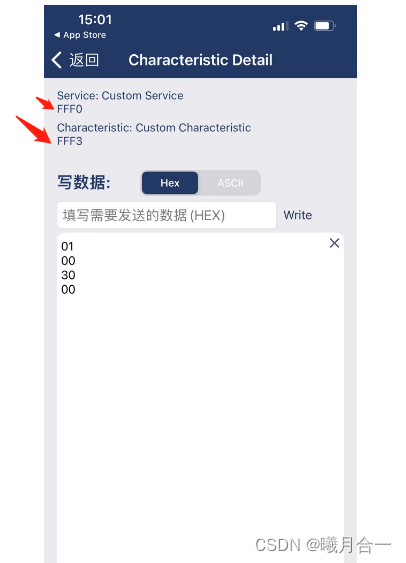
微信小程序 蓝牙设备连接,控制开关灯
1.前言 微信小程序中连接蓝牙设备,信息写入流程 1、检测当前使用设备(如自己的手机)是否支持蓝牙/蓝牙开启状态 wx:openBluetoothAdapter({}) 2、如蓝牙已开启状态,检查蓝牙适配器的状态 wx.getBluetoothAdapterState({}) 3、添加…...
Python 矢量数据库和矢量索引:构建 LLM 应用程序
推荐:使用 NSDT场景编辑器 助你快速搭建可二次编辑的3D应用场景 由于使用其硬件创建的生成式AI应用程序,Nvidia经历了显着的增长。另一项软件创新,矢量数据库,也正在乘着生成式人工智能的浪潮。 开发人员正在向量数据库上用Pytho…...

-Webkit-Box 在 Safari 中出现的兼容性问题
一、问题背景: UI要求要实现这样的效果,使用 display:-webket-box在chrome浏览器下完美解决 但是马上啪啪打脸,在safari浏览器下显示空白 ,不能不说浏览器之间的兼容性简直就是天坑 二、解决办法 通过浏览器调试发现原本float的…...
后端项目打包上传服务器记录
后端项目打包上传服务器记录 文章目录 后端项目打包上传服务器记录1、项目打包2、jar包上传服务器 本文记录打包一个后端项目,上传公司服务器的过程。 1、项目打包 通过IDEA的插件进行打包: 打成一个jar包,jar包的位置在控制台可以看到。 2、…...

ubuntu部署haproxy
HAProxy是可提供高可用性、负载均衡以及基于TCP和HTTP应用的代理. 1、更新系统报 通过在终端中运行以下命令,确保所有系统包都是最新的 sudo apt updatesudo apt upgrade2、安装Haproxy sudo apt install haproxy设置开机自动启动haproxy服务 sudo systemctl en…...
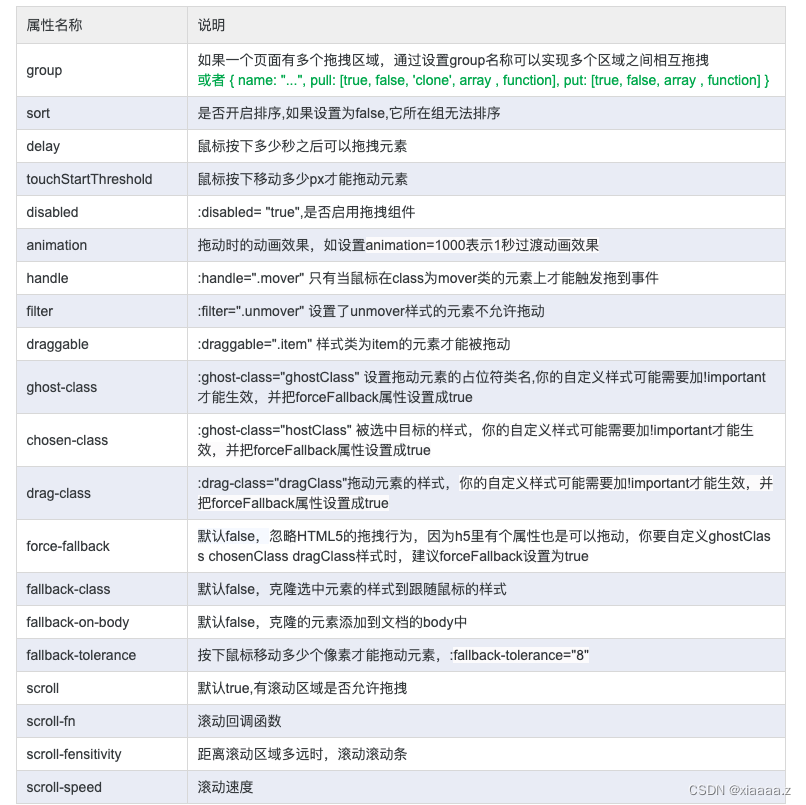
vue利用 sortable 完成表格拖拽
先讲一下vue2,使用sortable完成表格拖拽【不只是表格,div也可以实现,但我项目中是表格拖拽】 github地址 安装 npm install sortablejs --save使用 (我的项目中是拖拽一个小按钮移动,而不是整行) <te…...
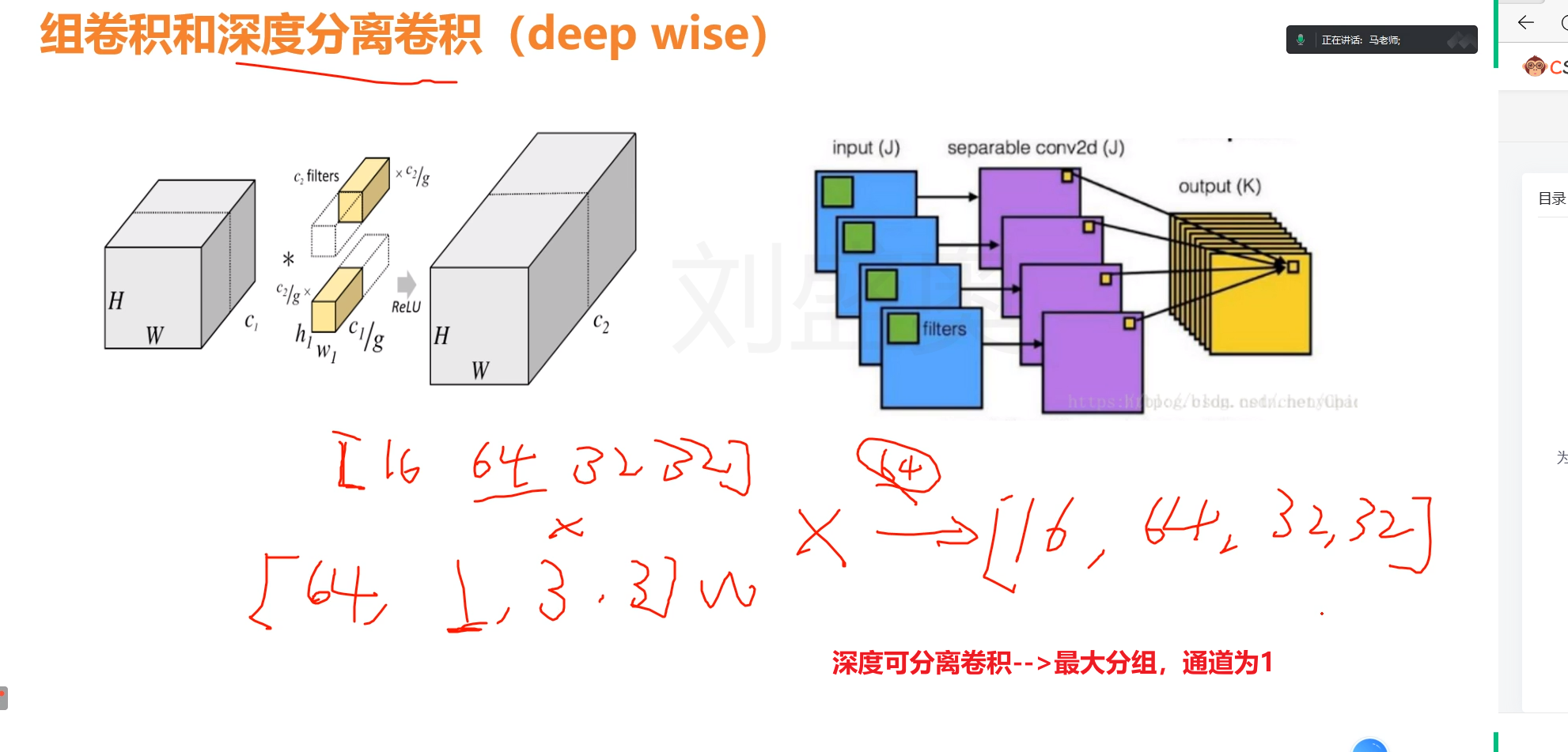
CNN简介3
...

新能源电动车充电桩控制主板安全特点
新能源电动车充电桩控制主板安全特点 你是否曾经担心过充电桩的安全问题?充电桩主板又是什么样的呢?今天我们就来聊聊这个话题。 充电桩主板采用双重安全防护系统,包括防水、防护、防尘等,确保充电桩安全、可靠。不仅如此,充电桩主板采用先…...

公路桥梁有哪些安全隐患?
在现代社会,公路桥梁作为连接城市、串联交通的重要纽带,扮演着无可替代的角色。然而,我们常常忽视的是,这些高架构筑物也存在着潜在的安全隐患,可能随时影响着交通的畅通和人们的生命财产安全。为了更好地认识和理解这…...

【C语言】每日一题(错误的集合)
最近在牛客、力扣上做题,花费海量时间,苦不堪言,有时绞尽脑汁也想不出,痛定思痛,每日记录写的比较困难的题。 错误的集合 题目如上图所示 题主乍看之下觉得很简单,再看例子,不就是一个有序数组…...

[JavaWeb]【四】web后端开发-SpringBootWeb入门
目录 一 Spring 二 SpringBootWeb入门 2.1 入门需求 2.2 分析 2.3 开始创建SpringBootWeb 2.4 创建类实现需求 2.5 启动程序 2.6 访问 三 HTTP协议 3.1 HTTP-概述 3.2 HTTP-请求协议 3.3 HTTP-响应协议 3.3.1 响应状态码 && 响应类型 3.4 HTTP-协议解析 前言…...

前端css
day03-CSS基础 目标:掌握 CSS 属性基本写法,能够使用文字相关属性美化文章页。 01-CSS初体验 层叠样式表 (Cascading Style Sheets,缩写为 CSS),是一种 样式表 语言,用来描述 HTML 文档的呈现(…...

vb+sql医院门诊管理系统设计与系统
摘要 信息时代已经来临,计算机应用于医院的日常管理,为医院的现代化带来了从未有过的动力和机遇,为医疗卫生领域的发展提供了无限的潜力。采用计算机管理信息系统已成为医院管理科学化和现代化的标志,给医院带来了明显的经济效益和社会效益。 本文介绍了数据库管理系统的…...

bootstrap-modal调用ajax后不经过回调函数
说明:我用的是boostrap的弹框,表单用的是layui的,个人觉得bootstrap比layui的弹框好看点,能自适应高度。 如图:点击保存后里面的内容不执行 原因:type用的是submit 解决:把submit改为button...
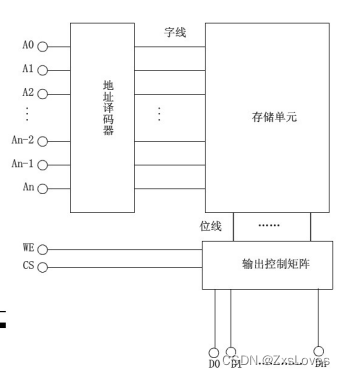
【【典型电路设计之片内存储器的设计之RAM的Verilog HDL描述一】】
典型电路设计之片内存储器的设计之RAM的Verilog HDL描述一 RAM是随机存储器,存储单元的内容可按需随意取出或存入。这种存储器在断电后将丢失所有数据,一般用来存储一些短时间内使用的程序和数据。 其内部结构如下图所示: 例:用…...
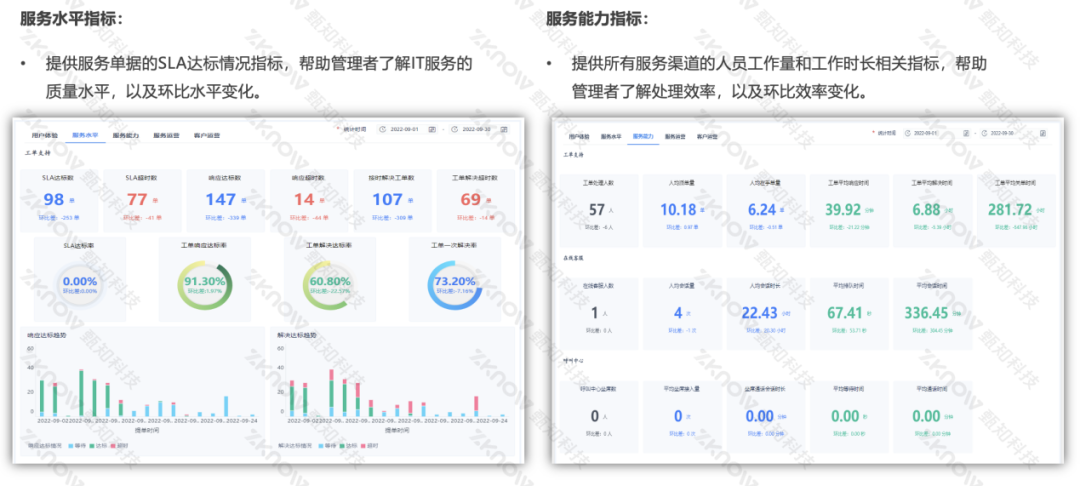
食品行业案例 | 燕千云助力头部食品企业搭建数智化 IT服务管理体系及平台
随着数字化时代的到来,食品行业呈现出多个发展趋势。首先,消费者对健康食品和功能性食品的关注度提高,推动了市场需求的增长。其次,便利食品和物流行业迅速发展,满足了快节奏生活的需求。再者,电商渠道和网…...
SpringBoot的日志信息及Lombok的常用注解
文章目录 一. 日志的介绍1. 什么是日志2. 日志的作用 二. 日志的使用1. 日志格式说明2. 自定义日志的输出3. 日志级别4. 日志级别的配置5. 日志持久化6. 更简单的输出日志-Lomok7. Lombok框架实现原理以及其他常见注解 一. 日志的介绍 1. 什么是日志 日志是我们程序重要组成部…...
Genoss GPT简介:使用 Genoss 模型网关实现多个LLM模型的快速切换与集成
一、前言 生成式人工智能领域的发展继续加速,大型语言模型 (LLM) 的用途范围不断扩大。这些用途跨越不同的领域,包括个人助理、文档检索以及图像和文本生成。ChatGPT 等突破性应用程序为公司进入该领域并开始使用这项技术进行构建铺平了道路。 大公司正…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...

RabbitMQ 各类交换机
为什么要用交换机? 交换机用来路由消息。如果直发队列,这个消息就被处理消失了,那别的队列也需要这个消息怎么办?那就要用到交换机 交换机类型 1,fanout:广播 特点 广播所有消息:将消息…...
