【JS 线性代数算法之向量与矩阵】
线性代数算法
- 一、向量的加减乘除
- 1. 向量加法
- 2. 向量减法
- 3. 向量数乘
- 4. 向量点积
- 5. 向量叉积
- 二、矩阵的加减乘除
- 1. 矩阵加法
- 2. 矩阵减法
- 3. 矩阵数乘
- 4. 矩阵乘法
- 常用数学库
线性代数是数学的一个分支,用于研究线性方程组及其解的性质、向量空间及其变换的性质等。在计算机科学领域中,线性代数常用于图形学、机器学习、计算机视觉等领域。本文将详细介绍 JS 中常用的线性代数算法,并提供代码示例。
一、向量的加减乘除
向量是有大小和方向的量,通常用一列数表示。向量的加减乘除运算也是线性代数中的基本运算。
1. 向量加法
向量加法计算两个向量相加的结果。
例如:给定两个二维向量:
a ⃗ = [ 1 2 ] , b ⃗ = [ 3 4 ] \vec{a}=\begin{bmatrix} 1 \\ 2 \end{bmatrix},\vec{b}=\begin{bmatrix} 3 \\ 4 \end{bmatrix} a=[12],b=[34]
则它们的和为:
a ⃗ + b ⃗ = [ 4 6 ] \vec{a}+\vec{b}=\begin{bmatrix} 4 \\ 6 \end{bmatrix} a+b=[46]
代码实现:
function addVectors(a, b) {if (a.length !== b.length) return null;return a.map((n, i) => n + b[i]);
}
2. 向量减法
向量减法计算两个向量相减的结果。
例如:给定两个三维向量:
a ⃗ = [ 1 3 2 ] , b ⃗ = [ 4 1 5 ] \vec{a}=\begin{bmatrix} 1 \\ 3 \\ 2 \end{bmatrix},\vec{b}=\begin{bmatrix} 4 \\ 1 \\ 5 \end{bmatrix} a= 132 ,b= 415
则它们的差为:
a ⃗ − b ⃗ = [ − 3 2 − 3 ] \vec{a}-\vec{b}=\begin{bmatrix} -3 \\ 2 \\ -3 \end{bmatrix} a−b= −32−3
代码实现:
function subtractVectors(a, b) {if (a.length !== b.length) return null;return a.map((n, i) => n - b[i]);
}
3. 向量数乘
向量数乘是将一个向量的每个元素乘以一个标量。
例如:给定一个三维向量:
a ⃗ = [ 1 3 2 ] \vec{a}=\begin{bmatrix} 1 \\ 3 \\ 2 \end{bmatrix} a= 132
则它乘以标量 k = 2 k=2 k=2 的结果为:
k a ⃗ = 2 [ 1 3 2 ] = [ 2 6 4 ] k \vec{a}=2\begin{bmatrix} 1 \\ 3 \\ 2 \end{bmatrix}=\begin{bmatrix} 2 \\ 6 \\ 4 \end{bmatrix} ka=2 132 = 264
代码实现:
function scalarMultiply(vector, scalar) {return vector.map(n => n * scalar);
}
4. 向量点积
向量点积(也称为内积或数量积)计算两个向量的乘积的和。
例如:给定两个三维向量:
a ⃗ = [ 1 3 2 ] , b ⃗ = [ 4 1 5 ] \vec{a}=\begin{bmatrix} 1 \\ 3 \\ 2 \end{bmatrix},\vec{b}=\begin{bmatrix} 4 \\ 1 \\ 5 \end{bmatrix} a= 132 ,b= 415
则它们的点积为:
a ⃗ ⋅ b ⃗ = 1 × 4 + 3 × 1 + 2 × 5 = 17 \vec{a} \cdot \vec{b}=1 \times 4 + 3 \times 1 + 2 \times 5 = 17 a⋅b=1×4+3×1+2×5=17
代码实现:
function dotProduct(a, b) {if (a.length !== b.length) return null;return a.reduce((sum, n, i) => sum + n * b[i], 0);
}
5. 向量叉积
向量叉积(也称为外积或向量积)计算两个向量的垂直于它们所在平面的法向量。向量叉积只适用于三维向量。
例如:给定两个三维向量:
a ⃗ = [ 1 3 2 ] , b ⃗ = [ 4 1 5 ] \vec{a}=\begin{bmatrix} 1 \\ 3 \\ 2 \end{bmatrix},\vec{b}=\begin{bmatrix} 4 \\ 1 \\ 5 \end{bmatrix} a= 132 ,b= 415
则它们的叉积为:
a ⃗ × b ⃗ = [ 13 3 − 11 ] \vec{a} \times \vec{b}=\begin{bmatrix} 13 \\ 3 \\ -11 \end{bmatrix} a×b= 133−11
代码实现:
function crossProduct(a, b) {if (a.length !== 3 || b.length !== 3) return null;const [ax, ay, az] = a;const [bx, by, bz] = b;return [ay * bz - az * by, az * bx - ax * bz, ax * by - ay * bx];
}
二、矩阵的加减乘除
矩阵是由若干行若干列的数排成的矩形阵列,通常用两个下标表示。矩阵的加减乘除运算也是线性代数中的基本运算。
1. 矩阵加法
矩阵加法计算两个矩阵相加的结果。
例如:给定两个 2 × 2 2 \times 2 2×2 的矩阵:
[ 1 2 3 4 ] , [ 5 6 7 8 ] \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} , \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} [1324],[5768]
则它们的和为:
[ 6 8 10 12 ] \begin{bmatrix} 6 & 8 \\ 10 & 12 \end{bmatrix} [610812]
代码实现:
function addMatrices(a, b) {if (a.length !== b.length || a[0].length !== b[0].length) return null;return a.map((row, i) => row.map((n, j) => n + b[i][j]));
}
2. 矩阵减法
矩阵减法计算两个矩阵相减的结果。
例如:给定两个 3 × 3 3 \times 3 3×3 的矩阵:
[ 1 3 2 4 8 5 6 1 2 ] , [ 2 1 5 3 6 4 1 7 3 ] \begin{bmatrix} 1 & 3 & 2 \\ 4 & 8 & 5 \\ 6 & 1 & 2 \end{bmatrix} , \begin{bmatrix} 2 & 1 & 5 \\ 3 & 6 & 4 \\ 1 & 7 & 3 \end{bmatrix} 146381252 , 231167543
则它们的差为:
[ − 1 2 − 3 1 2 1 5 − 6 − 1 ] \begin{bmatrix} -1 & 2 & -3 \\ 1 & 2 & 1 \\ 5 & -6 & -1 \end{bmatrix} −11522−6−31−1
代码实现:
function subtractMatrices(a, b) {if (a.length !== b.length || a[0].length !== b[0].length) return null;return a.map((row, i) => row.map((n, j) => n - b[i][j]));
}
3. 矩阵数乘
矩阵数乘是将一个矩阵的每个元素乘以一个标量。
例如:给定一个 2 × 2 2 \times 2 2×2 的矩阵:
[ 1 3 2 5 ] \begin{bmatrix} 1 & 3 \\ 2 & 5 \end{bmatrix} [1235]
则它乘以标量 k = 2 k=2 k=2 的结果为:
2 × [ 1 3 2 5 ] = [ 2 6 4 10 ] 2 \times \begin{bmatrix} 1 & 3 \\ 2 & 5 \end{bmatrix}=\begin{bmatrix} 2 & 6 \\ 4 & 10 \end{bmatrix} 2×[1235]=[24610]
代码实现:
function scalarMultiplyMatrix(matrix, scalar) {return matrix.map(row => row.map(n => n * scalar));
}
4. 矩阵乘法
矩阵乘法计算两个矩阵相乘的结果。矩阵乘法满足结合律,但不满足交换律。即 A × B ≠ B × A A \times B \neq B \times A A×B=B×A。
例如:给定两个 2 × 3 2 \times 3 2×3 和 3 × 2 3 \times 2 3×2 的矩阵:
[ 1 2 3 4 5 6 ] , [ 7 8 9 10 11 12 ] \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} , \begin{bmatrix} 7 & 8 \\ 9 & 10 \\ 11 & 12\end{bmatrix} [142536], 791181012
以下是两个 2×3 和 3×2 矩阵的乘法的 JavaScript 代码示例:
// 2x3 矩阵
const matrixA = [[1, 2, 3],[4, 5, 6]
];// 3x2 矩阵
const matrixB = [[7, 8],[9, 10],[11, 12]
];// 2x2 结果矩阵
const resultMatrix = [[0, 0],[0, 0]
];// 矩阵乘法
for (let i = 0; i < 2; i++) {for (let j = 0; j < 2; j++) {let sum = 0;for (let k = 0; k < 3; k++) {sum += matrixA[i][k] * matrixB[k][j];}resultMatrix[i][j] = sum;}
}// 输出结果
console.log(resultMatrix);
输出结果为:
[[58, 64],[139, 154]
]
上述代码中,我们首先定义了两个矩阵 matrixA 和 matrixB,然后定义了一个结果矩阵 resultMatrix,该矩阵的大小为 2×2。
接下来,我们通过三层循环实现了矩阵乘法。外层两个循环控制结果矩阵的行列数,内层循环计算结果矩阵中每个元素的值。
最后,我们输出了结果矩阵的值。
常用数学库
在 JavaScript 中实现线性代数算法需要使用数学库,比如 Math.js 或者 NumJS。
以下是 Math.js 的示例代码:
// 创建矩阵
const matrix1 = math.matrix([[1, 2], [3, 4]]);
const matrix2 = math.matrix([[5, 6], [7, 8]]);// 加法
const addResult = math.add(matrix1, matrix2);
console.log(addResult); // 输出 [[6, 8], [10, 12]]// 矩阵乘法
const multiplyResult = math.multiply(matrix1, matrix2);
console.log(multiplyResult); // 输出 [[19, 22], [43, 50]]// 转置
const transposeResult = math.transpose(matrix1);
console.log(transposeResult); // 输出 [[1, 3], [2, 4]]// 求逆矩阵
const inverseResult = math.inv(matrix1);
console.log(inverseResult); // 输出 [[-2, 1], [1.5, -0.5]]
以上是一些常见的线性代数算法的示例代码。使用数学库可以方便地实现复杂的线性代数计算。
相关文章:

【JS 线性代数算法之向量与矩阵】
线性代数算法 一、向量的加减乘除1. 向量加法2. 向量减法3. 向量数乘4. 向量点积5. 向量叉积 二、矩阵的加减乘除1. 矩阵加法2. 矩阵减法3. 矩阵数乘4. 矩阵乘法 常用数学库 线性代数是数学的一个分支,用于研究线性方程组及其解的性质、向量空间及其变换的性质等。在…...
配置 yum/dnf 置您的系统以使用默认存储库
题目 给系统配置默认存储库,要求如下: YUM 的 两 个 存 储 库 的 地 址 分 别 是 : ftp://host.domain8.rhce.cc/dvd/BaseOS ftp://host.domain8.rhce.cc/dvd/AppStream vim /etc/yum.repos.d/redhat.repo [base] namebase baseurlftp:/…...
Docker容器与虚拟化技术:Docker资源控制、数据管理
目录 一、理论 1.资源控制 2.Docker数据管理 二、实验 1.Docker资源控制 2.Docker数据管理 三、问题 1.docker容器故障导致大量日志集满,造成磁盘空间满 2、当日志占满之后如何处理 四、总结 一、理论 1.资源控制 (1) CPU 资源控制 cgroups࿰…...
python生成器有几种写法,python生成器函数例子
大家好,小编来为大家解答以下问题,python生成器有几种写法,python生成器函数例子,今天让我们一起来看看吧! 本文部分参考:Python迭代器,生成器–精华中的精华 https://www.cnblogs.com/deeper/p…...

动态动画弹窗样式css
点击下载图片素材 html <div class"popWin"> </div> <div class"popPic"><div class"popWinBtn01">查看证书</div><div class"wintips01">恭喜您已完成训练营学习任务,荣誉证书已发放…...
数据生成 | MATLAB实现WGAN生成对抗网络数据生成
数据生成 | MATLAB实现WGAN生成对抗网络数据生成 目录 数据生成 | MATLAB实现WGAN生成对抗网络数据生成生成效果基本描述程序设计参考资料 生成效果 基本描述 1.WGAN生成对抗网络,数据生成,样本生成程序,MATLAB程序; 2.适用于MATL…...
PHP实现每日蛋白质摄入量计算器
1.laravel 路由 //每日蛋白质摄入计算器Route::get(api/protein/intake, FormulaControllerproteinIntakeCal); 2.代码 /*** 每日蛋白质摄入计算器*/public function proteinIntakeCal(){$number intval($this->request(number));$goalFactor array(0.8, 1.16, 0.8, 1.16,…...

vue elment 表格内表单校验代码
<p v-if"scope.row.id">{{ scope.row.bidderCode }}</p><el-form-itemclass"formitem"v-else:prop"bidderCode scope.row.id":rules"getValidationRules(投标人/供应商代码, scope.row.id)"><el-input v-model&…...

如何在Stream流中分组统计
上面是今天碰到需求,之前就做过类似的分组统计,这个相对来说比较简单,统计的也少,序号和总预约人数这两部分交给前端了,不需要由后端统计,后端统计一下预约日期和检查项目和预约人数就行; Overridepublic List<ItemStatisticsVo> statistics(ItemStatisticsModel itemSta…...
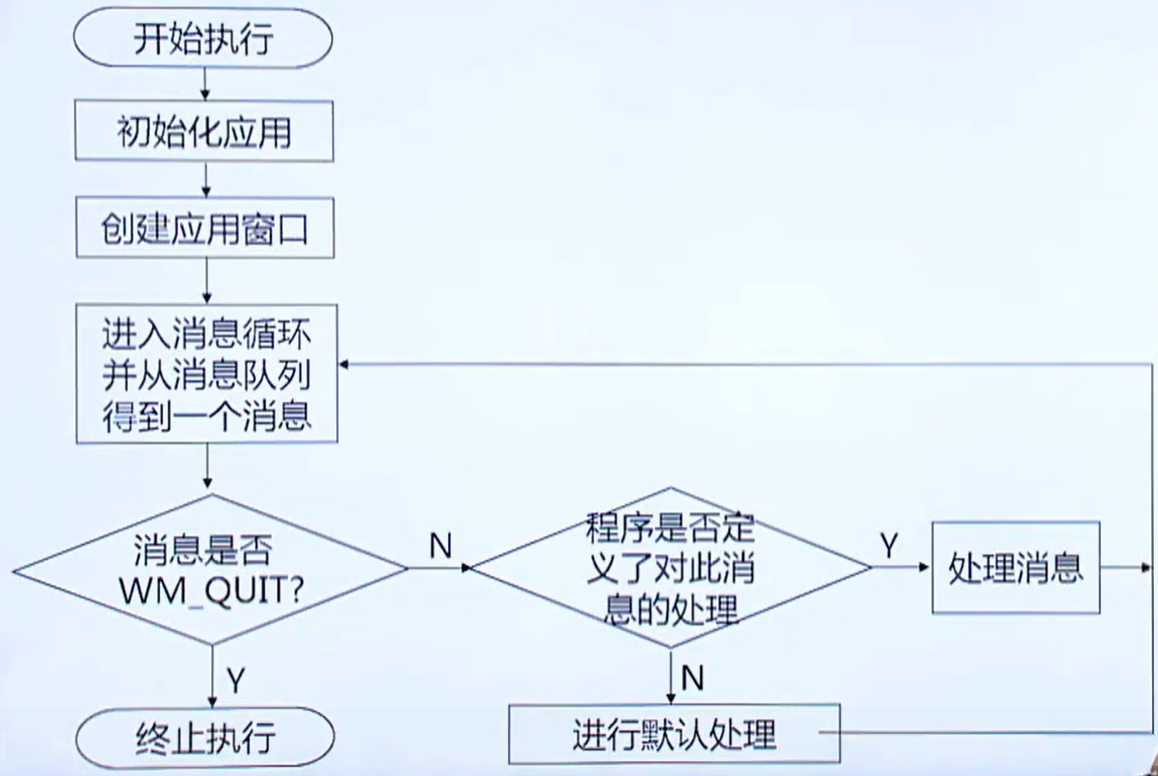
windows程序基础
一、windows程序基础 1. Windows程序的特点 1)用户界面统一、友好 2)支持多任务:允许用户同时运行多个应用程序(窗口) 3)独立于设备的图形操作 使用图形设备接口( GDI, Graphics Device Interface )屏蔽了不同硬件设备的差异&#…...

【LeetCode】买卖股票的最佳时机最多两次购买机会
买卖股票的最佳时机 题目描述算法分析程序代码 链接: 买卖股票的最佳时机 题目描述 算法分析 程序代码 class Solution { public:int maxProfit(vector<int>& prices) {int n prices.size();vector<vector<int>> f(n,vector<int>(3,-0x3f3f3f))…...

【C++ 记忆站】命名空间
文章目录 命名空间概念命名空间的定义1、正常的命名空间定义2、命名空间可以嵌套3、同一个工程中允许存在多个相同名称的命名空间,编译器最后会合成同一个命名空间中 命名空间的使用1、加命名空间名称及作用域限定符2、使用using将命名空间中某个成员引入3、使用using namespac…...

《离散数学及其应用(原书第8版)》ISBN978-7-111-63687-8 第11章 11.1.3 树的性质 节 第664页的例9说明
《离散数学及其应用(原书第8版)》ISBN978-7-111-63687-8 第11章 11.1.3 树的性质 节 第664页的定理3的引申 定理3 带有i个内点的m叉树含有nmi1个顶点 见本人博文 内点定义不同的讨论 如果对于一个m叉正则树,即任意分支节点的儿子恰好有m个&am…...

【云原生】K8S存储卷:PV、PVC详解
目录 一、emptyDir存储卷二、hostPath存储卷三、nfs共享存储卷四、PVC 和 PV4.1 NFS使用PV和PVC4.2创建动态PV 一、emptyDir存储卷 容器磁盘上的文件的生命周期是短暂的,这就使得在容器中运行重要应用时会出现一些问题。首先,当容器崩溃时,ku…...
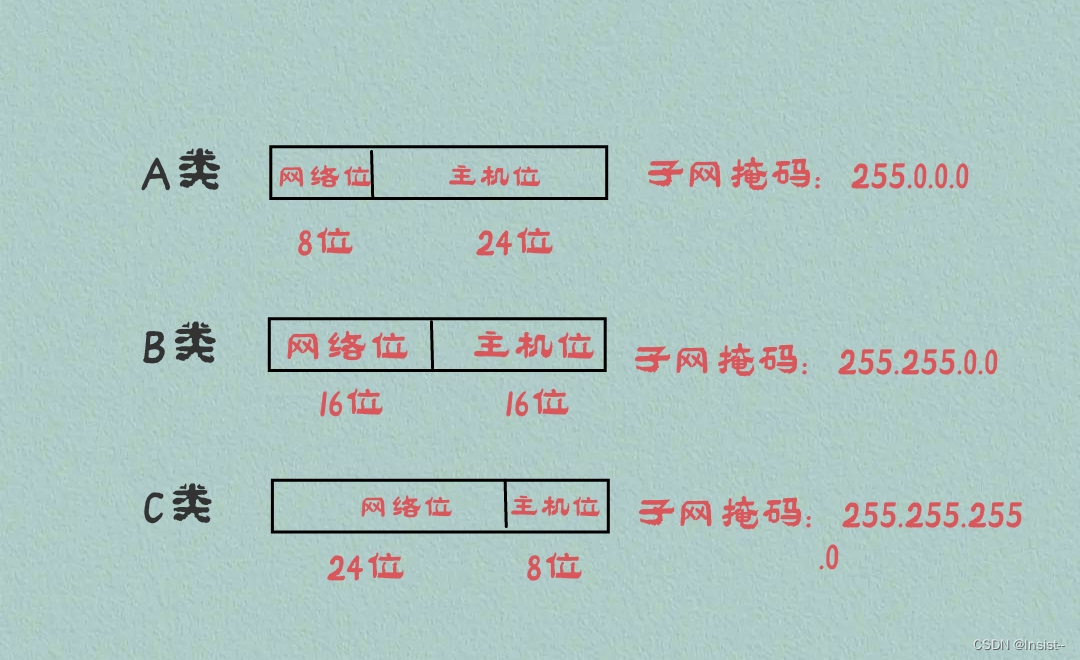
谈谈IP地址和子网掩码的概念及应用
个人主页:insist--个人主页 本文专栏:网络基础——带你走进网络世界 本专栏会持续更新网络基础知识,希望大家多多支持,让我们一起探索这个神奇而广阔的网络世界。 目录 一、IP地址的概念 二、IP地址的分类 1、A类 …...

vue2 如何监听数组的变化
在Vue 2中,底层是通过重写数组的原型方法来实现对数组变化的监听。具体来说,Vue 2使用了一个名为Observer的类来劫持数组的原型方法,使其在调用这些方法时能够触发相应的变化通知。 当Vue 2初始化一个响应式对象时,如果对象是一个…...

CSS中的transform属性有哪些值?并分别描述它们的作用。
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ translate()⭐ rotate()⭐ scale()⭐ skew()⭐ matrix()⭐ scaleX() 和 scaleY()⭐ rotateX()、rotateY() 和 rotateZ()⭐ translateX() 和 translateY()⭐ skewX() 和 skewY()⭐ perspective()⭐ 写在最后 ⭐ 专栏简介 前端入门之旅&…...

vue3跳转页面后 海康监控实例不销毁
第一个页面是这样的 跳转到新的页面 只有海康的监控没有消失 使用控制台审查元素也审查不到 解决方法:在vue3的销毁周期把海康的监控销毁掉 import { reactive, onDeactivated} from "vue"; const state reactive({oWebControl: null as any, //监控绑…...
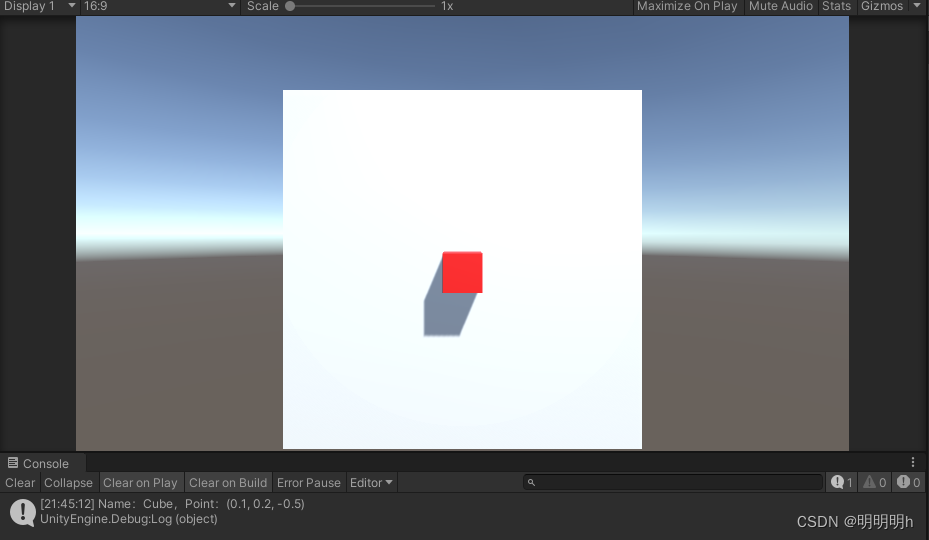
Unity 射线检测
文章目录 1. 定义2. 重要类和方法2.1 Ray2.2 从屏幕发出射线:2.3 Raycast2.4 RaycastAll2.5 RaycastHit 碰撞信息2.6 layerMask 让射线检测只检测指定层级的对象 1. 定义 在Unity中,射线检测(Raycasting)是一种常用的技术&#x…...
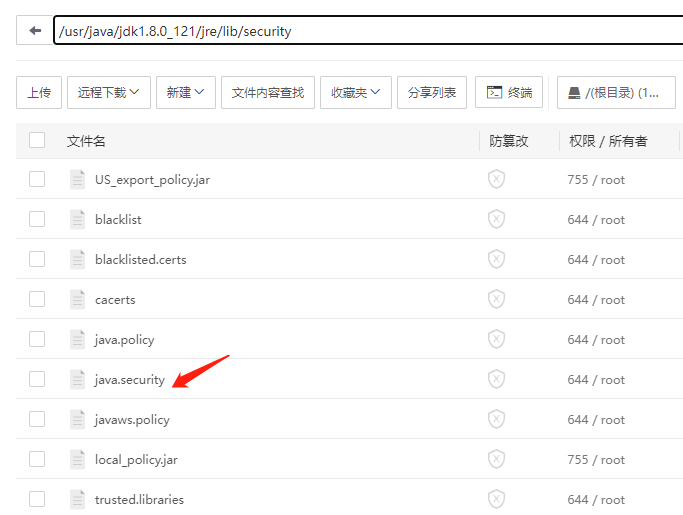
微信支付报非法的密钥大小: Caused by: java.security.InvalidKeyException: Illegal key size
在Linux环境中出现 java.security.InvalidKeyException: Illegal key size 异常通常是由于Java默认的加密限制引起的。Java默认的加密强度限制了加密算法密钥的最大长度 方式一 1. 找到该目录 /usr/java/jdk1.8.0_121/jre/lib/security 2. 替换local_policy.jar 和 US_export_…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
