leetcode 279. 完全平方数
2023.8.18
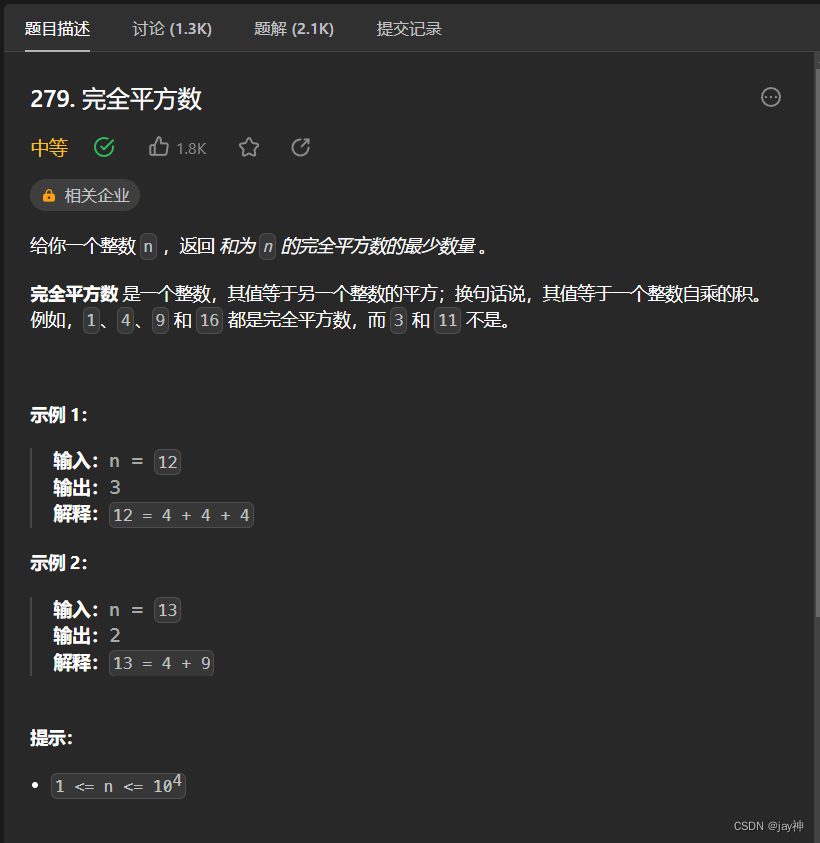
与零钱兑换相似,本题属于完全背包问题:完全平方数为物品,整数n为背包。
直接上代码:
class Solution {
public:int numSquares(int n) {vector<int> dp(n+1 , INT_MAX);dp[0] = 0;for(int i=1; i*i<=n; i++){for(int j=i*i; j<=n; j++){dp[j] = min(dp[j] , dp[j-i*i]+1);}} return dp[n]; }
};相关文章:

leetcode 279. 完全平方数
2023.8.18 与零钱兑换相似,本题属于完全背包问题:完全平方数为物品,整数n为背包。 直接上代码: class Solution { public:int numSquares(int n) {vector<int> dp(n1 , INT_MAX);dp[0] 0;for(int i1; i*i<n; i){for(in…...
【从零学习python 】48.Python中的继承与多继承详解
文章目录 在Python中,继承可以分为单继承、多继承和多层继承。单继承 继承语法多继承 语法格式使用多继承时需要注意以下事项Python中的MRO新式类和旧式(经典)类 进阶案例 在Python中,继承可以分为单继承、多继承和多层继承。 单…...
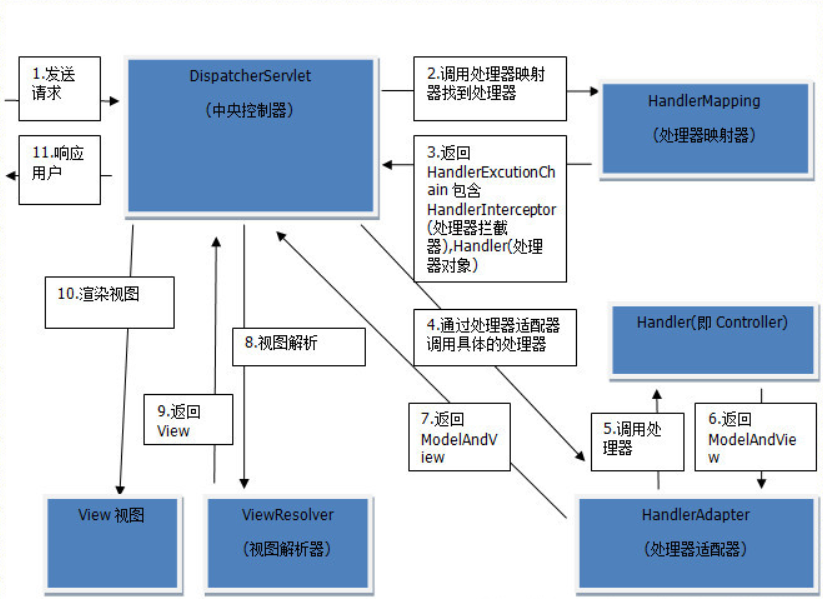
二、编写第一个 Spring MVC 程序(总结项目报 404 问题以及 Spring MVC 的执行流程)
文章目录 一、编写第一个 Spring MVC 程序二、项目运行时报 404错误原因总结三、Spring MVC 的执行流程 一、编写第一个 Spring MVC 程序 创建 maven 项目,以此项目为父项目,在父项目的 pom.xml 中导入相关依赖 <dependencies><dependency…...

okhttp源码简单流程分析
拦截器详细解析可以看大佬简书 "https://www.jianshu.com/p/6fac73f7570f"和 “https://www.jianshu.com/p/3c740829475c” okhttp请求流程 1:OkHttpClient okHttpClient new OkHttpClient.Builder() 构建一个okhttpClient对象,传入你想传入的…...
SpringBoot整合Shiro实现登录认证,鉴权授权
文章目录 前言一、shiro简介二、环境搭建2.1.数据库2.1.1user用户表2.1.2user_role用户角色关系表2.1.3role角色表2.1.4role_permission角色权限关系表2.1.5permission权限表 2.2导坐标2.3实体类2.3.1User2.3.2Role2.3.3Permission 2.4MVC三层2.4.1User2.4.1.1mapper层2.4.1.2s…...
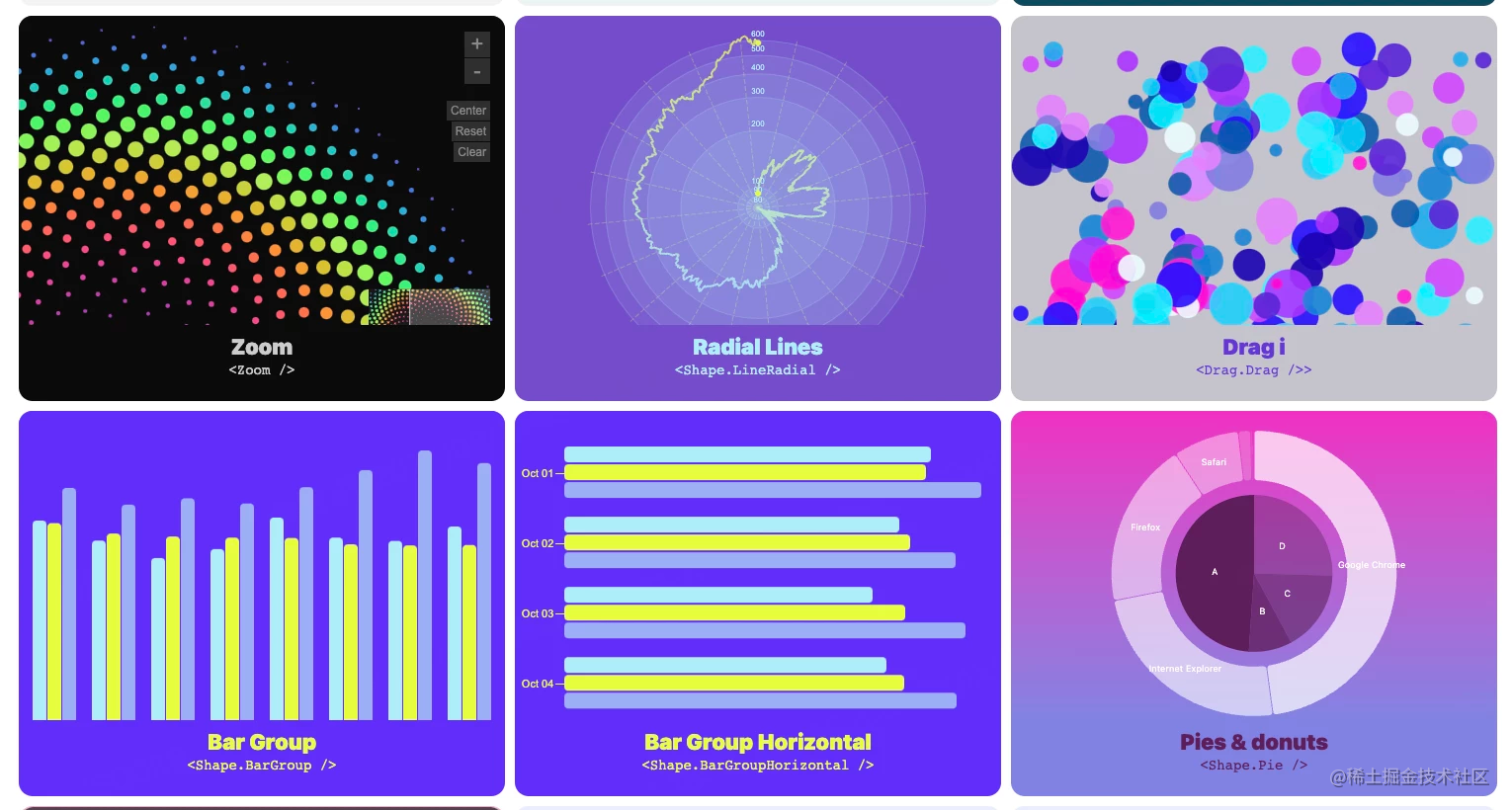
Airbnb开源数据可视化工具Visx
一、什么是visx visx 是用于 React 的富有表现力的底层可视化组件集合,结合了 d3 的强大功能来生成可视化,以及 React 更新 DOM 的诸多优势。 在 Airbnb 内部,visx 的目标是统一整个公司的可视化堆栈,在此过程中,创建了 visx 项目,从而有效的将 D3 的强大功能与 React …...
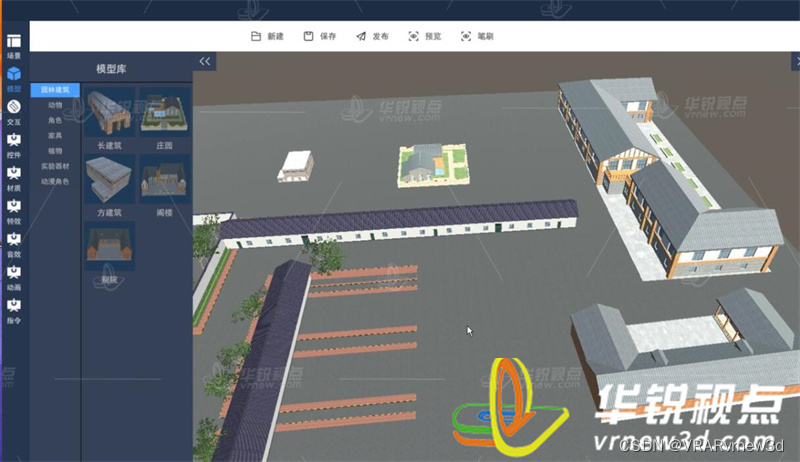
VR仿真实训系统编辑平台赋予老师更多自由和灵活性
为了降低院校教师在VR虚拟现实方面应用的门槛,VR公司深圳华锐视点融合多年的VR虚拟仿真实训系统制作经验,制作了VR动物课件编辑器,正在逐渐受到师生们的关注和应用。 简单来说,VR畜牧专业课件编辑器是一种可以制作虚拟现实动物教学…...

父类对象转成子类对象
import org.springframework.beans.BeanUtils; import java.util.ArrayList; import java.util.List; public class Test {public static void main(String[] args) {List<B> bList new ArrayList<>();B b new B("a","这是a","b",…...

Spring Boot中如何使用Flyway进行数据库迁移
在本文中,我们将了解如何使用 Flyway 来管理 Spring Boot 应用程序中的 SQL 数据库架构。 在本文中,我们将了解如何使用 Flyway 来管理Spring Boot应用程序中的SQL 数据库架构。 Flyway是一个数据库迁移工具,它提供迁移历史和回滚的功能&…...
)
web在线编辑器(vue版)
目录 前言一、monaco-editor1、源码2、体积优化 二、ace-editor?1、源码2、体积优化 总结 前言 提示:这里可以添加本文要记录的大概内容: 例如:随着人工智能的不断发展,机器学习这门技术也越来越重要,很多…...
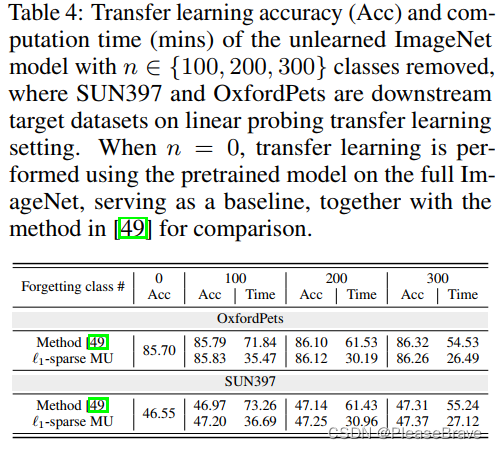
【论文阅读】 Model Sparsity Can Simplify Machine Unlearning
Model Sparsity Can Simplify Machine Unlearning 背景主要内容Contribution Ⅰ:对Machine Unlearning的一个全面的理解Contribution Ⅱ:说明model sparsity对Machine Unlearning的好处Pruning方法的选择sparse-aware的unlearning framework Experiments…...
Spring Clould 部署 - Docker
视频地址:微服务(SpringCloudRabbitMQDockerRedis搜索分布式) 初识Docker-什么是Docker(P42,P43) 微服务虽然具备各种各样的优势,但服务的拆分通用给部署带来了很大的麻烦。 分布式系统中&…...

linux--链表动态创建
头插法: 核心代码: s->next head->next; head->next s; 尾插法 核心代码: tail head; s->next NULL; tail->next s; tail s; 当用头插法依次插入值分别为1,2,3,4,5的结点后, 单链表顺序为: he…...

iBooker 布客技术评论 20230818
一、程序员自检手册 为了避免焦虑,你首先需要做的就是梳理你的业务: (1)你所在的行业是轻资产还是重资产? 重资产就是人绕着机器转,创业需要买一大堆设备。如果是重资产,赶紧换一个。 &…...

CK-A60180、CK-B1542、CK-L3095单向离合器
CK-A1542、CK-A1747、CK-A2052、CK-A2652、CK-A3072、CK-A3580、CK-A4090、CK-A45100、CK-A450110、CK-A60130、CK-A65140、CK-A70150、CK-A75160、CK-A80170、CK-A1250、CK-A1855、CK-A2060、CK-A2563、CK-A2563T、CK-A2870、CK-A3080T、CK-A3585、CK-A35100、CK-A35140、CK-A…...
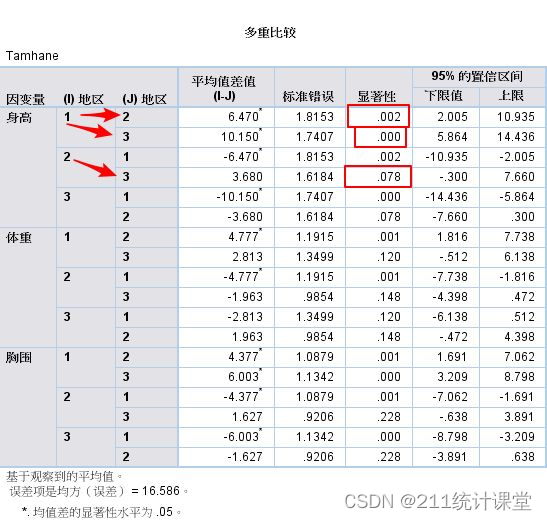
单因素多变量方差分析
多变量方差分析:是对多个独立变量是否受单个或多个因素影响而进行的方差分析。它不仅能够分析多个因素对观测变量的独立影响,更能够分析多个因素的交互作用能否对观测变量产生影响。本章以单因素多变量分析为例,即一个分组变量和多个欲分析的…...

Python Web:Django、Flask和FastAPI框架对比
原文:百度安全验证 Django、Flask和FastAPI是Python Web框架中的三个主要代表。这些框架都有着各自的优点和缺点,适合不同类型和规模的应用程序。 1. Django: Django是一个全功能的Web框架,它提供了很多内置的应用程序和工具&am…...

【CI/CD】Rancher K8s
Rancher & K8s Rancher 和 K8s 的关系是什么?K8s 全称为 Kubernetes,它是一个开源的,用于管理云平台中多个主机上的容器化的应用。而 Rancher 是一个完全开源的企业级多集群 Kubernetes 管理平台,实现了 Kubernetes 集群在混合…...

nodejs 之 express 实现下载网络图片并上传到七牛云对象存储oss空间
为方便阅读,本文将所有逻辑放在一个函数里,可根据自己的情况拆分。 安装依赖 在项目根目录下运行以下命令安装依赖 npm install express qiniu axios业务逻辑 在项目根目录下创建一个名为 app.js 的文件,并添加以下内容 const express re…...

综合能源系统(7)——综合能源综合评估技术
综合能源系统关键技术与典型案例 何泽家,李德智主编 综合能源系统是多种能源系统非线性耦合的、多时间与空间尺度耦合的“源-网-荷一储”一体化系统,通过能源耦合、多能互补,能够实现能源的高效利用,并提高新能源的利用水平。对…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...

jieba实现和用RNN实现中文分词的区别
Jieba 分词和基于 RNN 的分词在技术路线、实现机制、性能特点上有显著差异,以下是核心对比: 1. 技术路线对比 维度Jieba 分词RNN 神经网络分词范式传统 NLP(规则 统计)深度学习(端到端学习)核心依赖词典…...
