【查找算法】解析学习四大常用的计算机查找算法 | C++
第二十二章 四大查找算法
目录
第二十二章 四大查找算法
●前言
●查找算法
●一、顺序查找法
1.什么是顺序查找法?
2.案例实现
●二、二分查找法
1.什么是二分查找法?
2.案例实现
●三、插值查找法
1.什么是插值查找法?
2.案例实现
●四、斐波那契查找法
1.什么是斐波那契查找法?
2.案例实现
●总结
前言
在数据处理的过程中,能否在最短时间内去找到目的数据,是编程开发人员非常值得关心的一个问题。所谓查找,也被称为搜索,它是指从数据文件中找出满足某些条件的记录。在数据结构中描述算法时习惯用“查找”,而在搜索引擎中找信息或资料时习惯用“搜索”。我们在电话簿中查找某人的电话号码,电话簿就像是数据文件库,而姓名就是去查找电话号码的键值。我们经常使用的搜索引擎所设计的Spider程序(网页抓取程序爬虫)会主动经由网站上的超链接“爬行”到另一个网站,搜集每个网站上的信息并且收录到数据库中,这其中就涉及到了今天要讲的查找算法。
查找算法
在查找算法中,比较常见的有顺序法、二分法、插入法和斐波那契法等。查找的操作和算法有关,具体的操作方式和进行方式与所选择的数据结构有关。计算机查找数据的优点就是快速,但是对于不同程度下的数据量,查找可以分为内部查找(数据量较小的文件)和外部查找(数据量较大的文件)。影响查找时间长短的主要因素有算法,数据存储的方式以及结构。查找可以分为静态查找和动态查找。静态查找是指数据元素在查找的过程中不会有添加,删除,更新等操作。动态查找是指所查找的数据在查找过程中会经常地添加,删除或更新。
一、顺序查找法
1.什么是顺序查找法?
(1)简要介绍
顺序查找法是一种比较简单的查找法。该算法就是利用了计算机便于处理大量数据的这一特点,从而来进行实现的。该方法的优点就是文件在查找前不需要进行任何处理与排序;而缺点是查找的速度比较慢,因为无论数据顺序是什么情况,它都需要从头到尾都去遍历一遍。如果数据元素没有重复,那么找到数据元素就可以中止查找。说明最差的情况是n次查找,最好的情况下是1次查找。
(2)具体情况
在8个数据元素中,去顺序查找元素89。情况如下图所示:
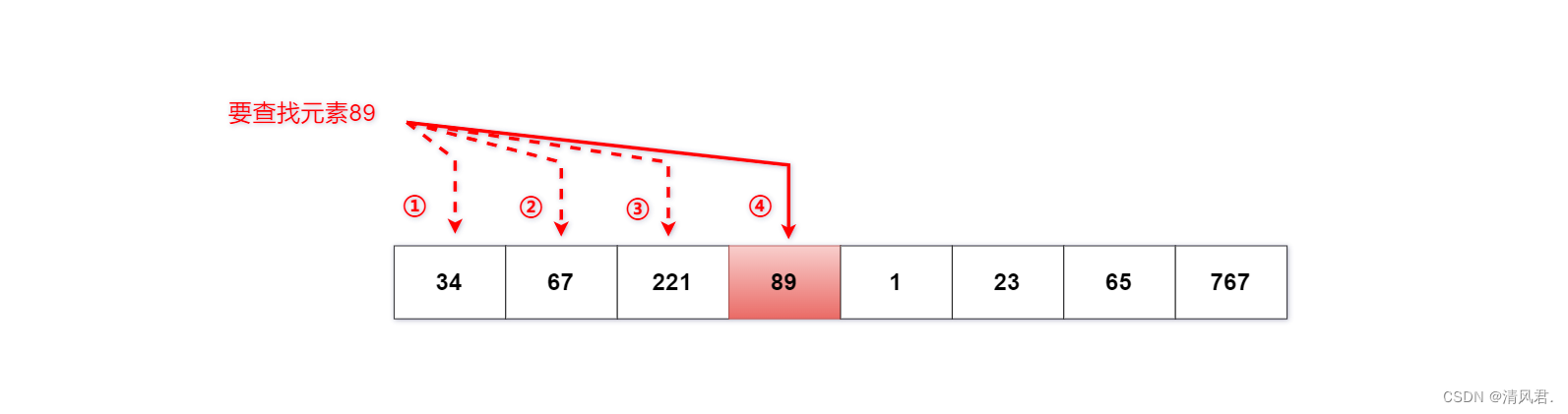
对于大量重复的数据元素来说,顺序查找法一般是不会使用的,因为它的时间效率极低并且可能会因为元素中的重复项而造成错误。但是对于少量的数据元素来说,这无疑是一种非常快又准确性高的简单方法。
(3)算法分析
①时间复杂度:如果数据没有重复且找到数据就可以中止,那么在最差情况下就是未找到数据,进行了n次比较,所以时间复杂度为O(n)。
②当数据量很大时,不适合使用顺序查找法。如果事先预估到所查找的数据在文件前面的部分,就可以减少查找的时间。
③在平均情况下,假设数据出现的概率相等,则需要进行(n+1)/2次比较。
2.案例实现
(1)范例情况:用随机法生成80个1~100的整数,用顺序查找法去查找我们指定元素是否存在,如果存在说明其所在的位置。
(2)代码展示:
#include<iostream>
#include<cstdlib>
using namespace std;
class order {
public:int data[80];int val = 0;//构造函数 随机给data中分配数据order() {for (int i = 0; i < 80; i++)data[i] = (rand() % 100) + 1;}void order_start() {cout << "请输入要猜测的数:";cin >> val;for (int i = 0; i < 80; i++){if (data[i] == val) {cout << "该数" << data[i] << "存在 所在位置为" << i + 1 << endl;val = 0;}}if (val != 0)cout << "该数不存在" << endl;}//析构函数 展现所有元素~order() {cout << "所有随机数据元素如下:" << endl;for (int i = 0; i < 80; i++) cout << data[i] << "[" << i << "]" << " ";}
};
int main()
{order o;while (o.val != -1){o.order_start();}
}(3)结果展示:
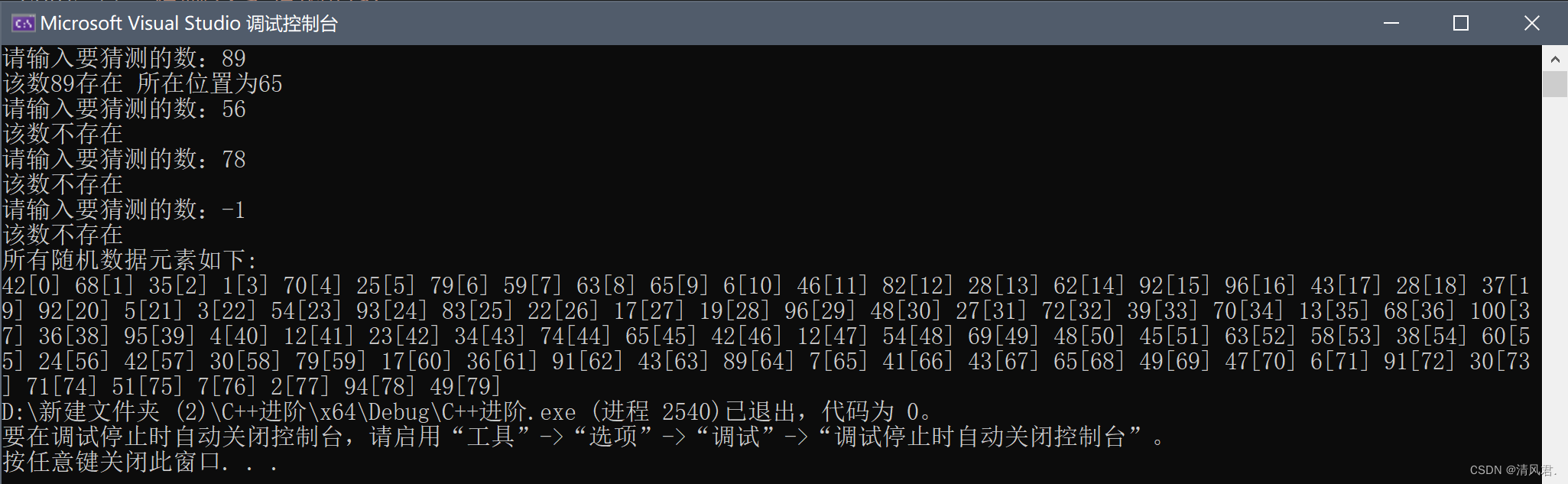
二、二分查找法
1.什么是二分查找法?
(1)简要介绍
如果一组数据已经事先排好了顺序,那么就可以用二分查找法来进行查找。二分查找法的基本方法就是将数据分成两等份,比较目标寻找值与中间值的大小。如果小于中间值,那么我们就可以确定要寻找的数据在前半部分,否则在后半部分。重复上述步骤将其分割直到找到或确定不存在为止。
(2)具体情况
用二分查找法对已经完成排序的一组数列,查找其元素101所在的位置。具体情况如下图所示:
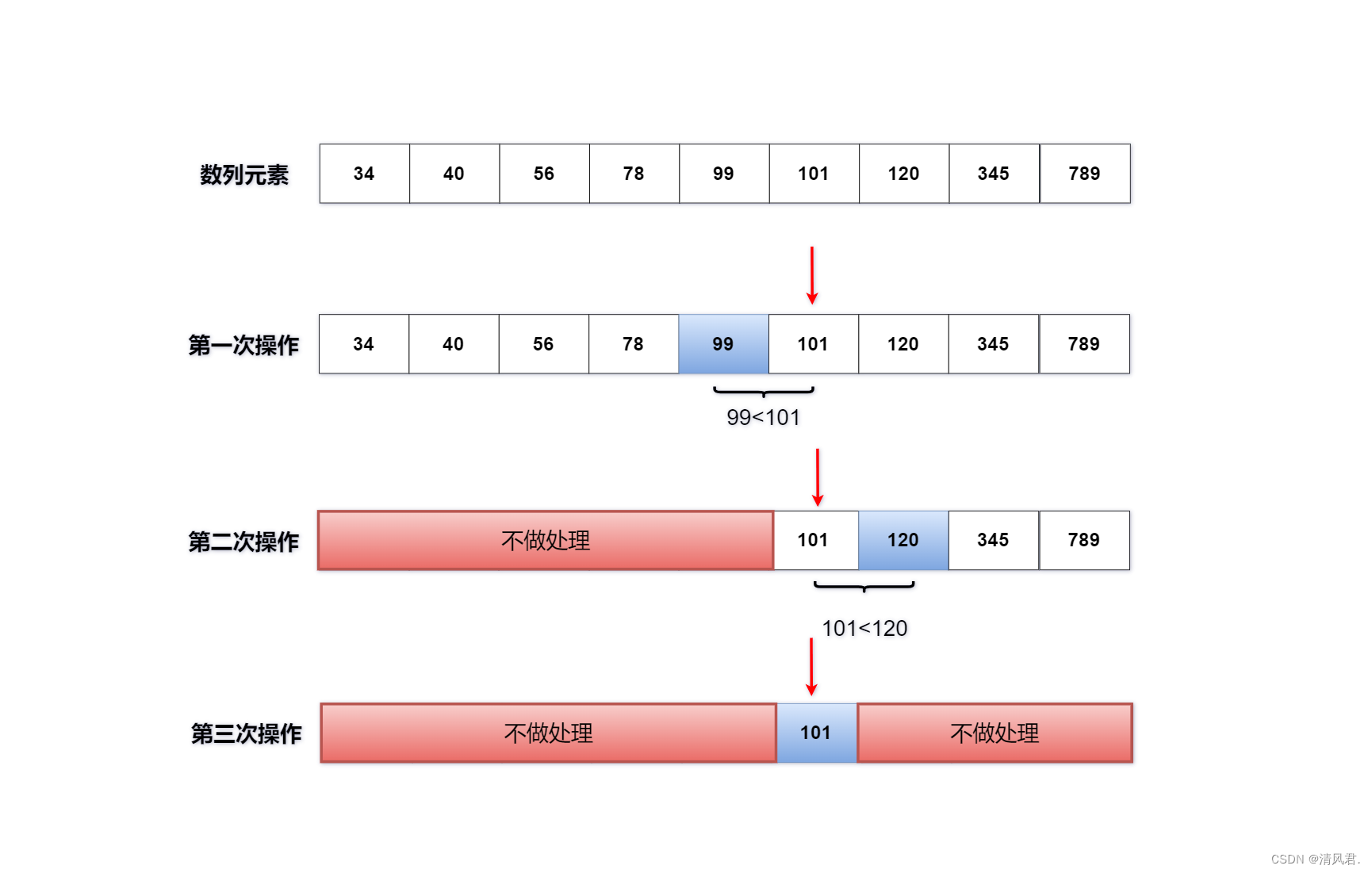
(3)算法分析
①时间复杂度:因为每次的查找都会比上一次查找少一半的范围,所以最多只需比较(log2^n)+1或(log2^(n+1))次,时间复杂度O(log2^n)。
②二分查找法必须是经过排序的数列,且数据元素都要加载到内存中才能进行查找。
③二分查找法适用于不需要增删的静态数据。
2.案例实现
(1)范例程序:用二分查找法查找10个1~10随机数据中指定数据元素的位置,并且输出随机产生的这10个数据。
(2)代码展示:
#include<iostream>
using namespace std;
#define size 10
class dichotomy {
public:int data[size];int val = 0;dichotomy() {for (int i = 0; i < size; i++)data[i] = (rand() % 10) + 1;}void sort() {for (int i = 0; i < size-1; i++) {for (int j = i+1; j < size; j++) {if (data[i] > data[j]){int temp;temp = data[i];data[i] = data[j];data[j] = temp;}}}}void dichotomy_start(int len_left,int len_right){ int record=0;while (len_left <= len_right ){int mid = (len_right + len_left) / 2;if (val < data[mid]) {cout << "目标数在中间值的左边" << endl;len_right = mid - 1;}else if (val > data[mid]) {cout << "目标数在中间值的右边" << endl;len_left = mid + 1;}else if(val==data[mid]){cout << "在第" << mid + 1 << "个位置处找到了" << "该元素" << data[mid] << endl;val = 1;break;} } if (val != 1) {cout << "随机产生的这几个数中不存在要猜测的这个数值" << endl;}}~dichotomy() {cout << "所有随机数据元素如下:" << endl;for (int i = 0; i < size; i++) cout << data[i] << "[" << i << "]" << " ";}
};
int main()
{dichotomy d;d.sort();while (d.val!=-1){cout << "请输入要猜测的数:";cin >> d.val;if (d.val != -1)d.dichotomy_start(0, size - 1);elsebreak;}
}
(3)结果展示:
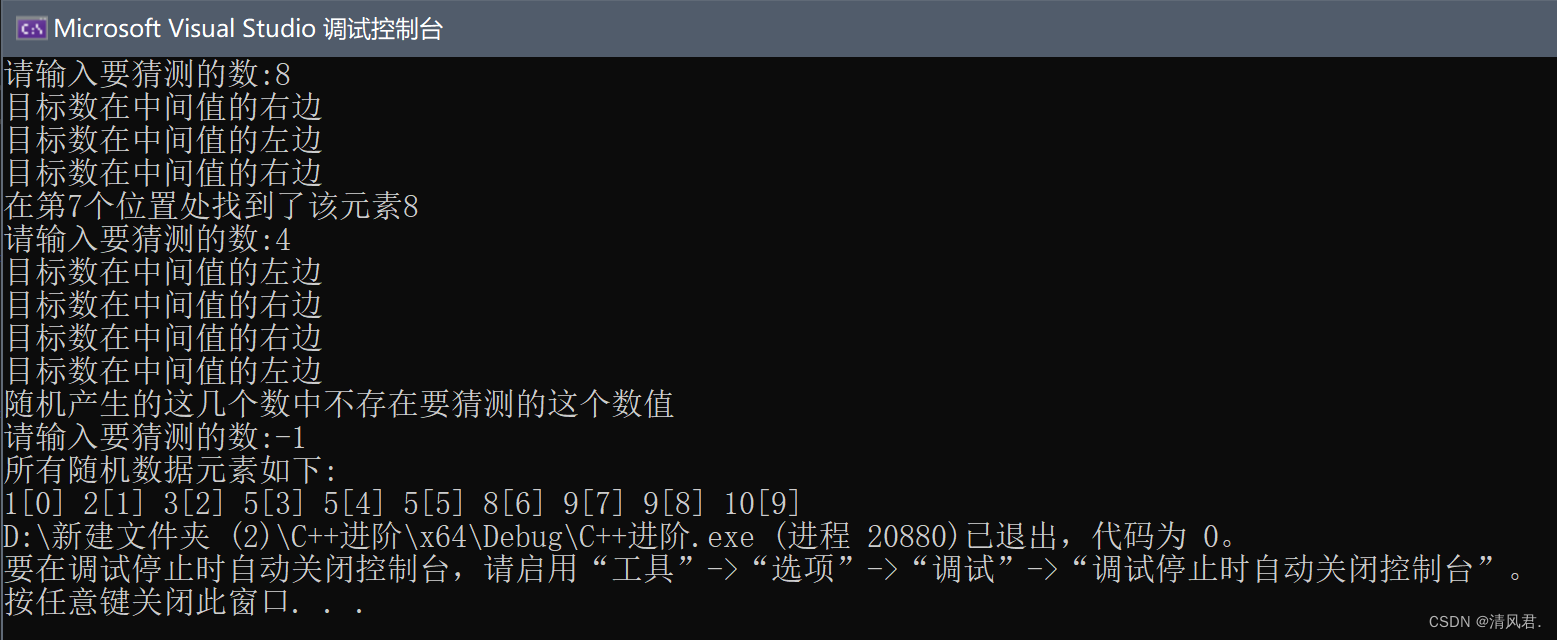
三、插值查找法
1.什么是插值查找法?
(1)简要介绍
插值查找法又被称为插补查找法,是对二分查找的进一步改进。它是按照数据位置的分布,利用公式去预测数据所在的位置,再用二分法的方式渐渐逼近。该查找法的公式如下:

其中,key是要去查找的键值,data[high],data[low]是剩余待查找记录中的最大值和最小值。特别注意:使用该查找算法之前需要对要排序的数据进行排序。
(2)具体情况
假设数据项为n,其插值查找法的步骤如下:
①讲记录从小到大的顺序给予1,2,...,n的编号;
②令low=1,high=n;
③当low<high时,重复执行步骤④和步骤⑤;
④令Mid=low+((key-data[low])/(data[high]-data[low]))*(high-low);
⑤若key<key[mid]且high≠Mid-1,则令high=Mid-1;
⑥若key>key[mid]且low≠Mid+1,则令low=Mid+1;
⑦若key=key[mid],则表示成功找到了键值的位置;
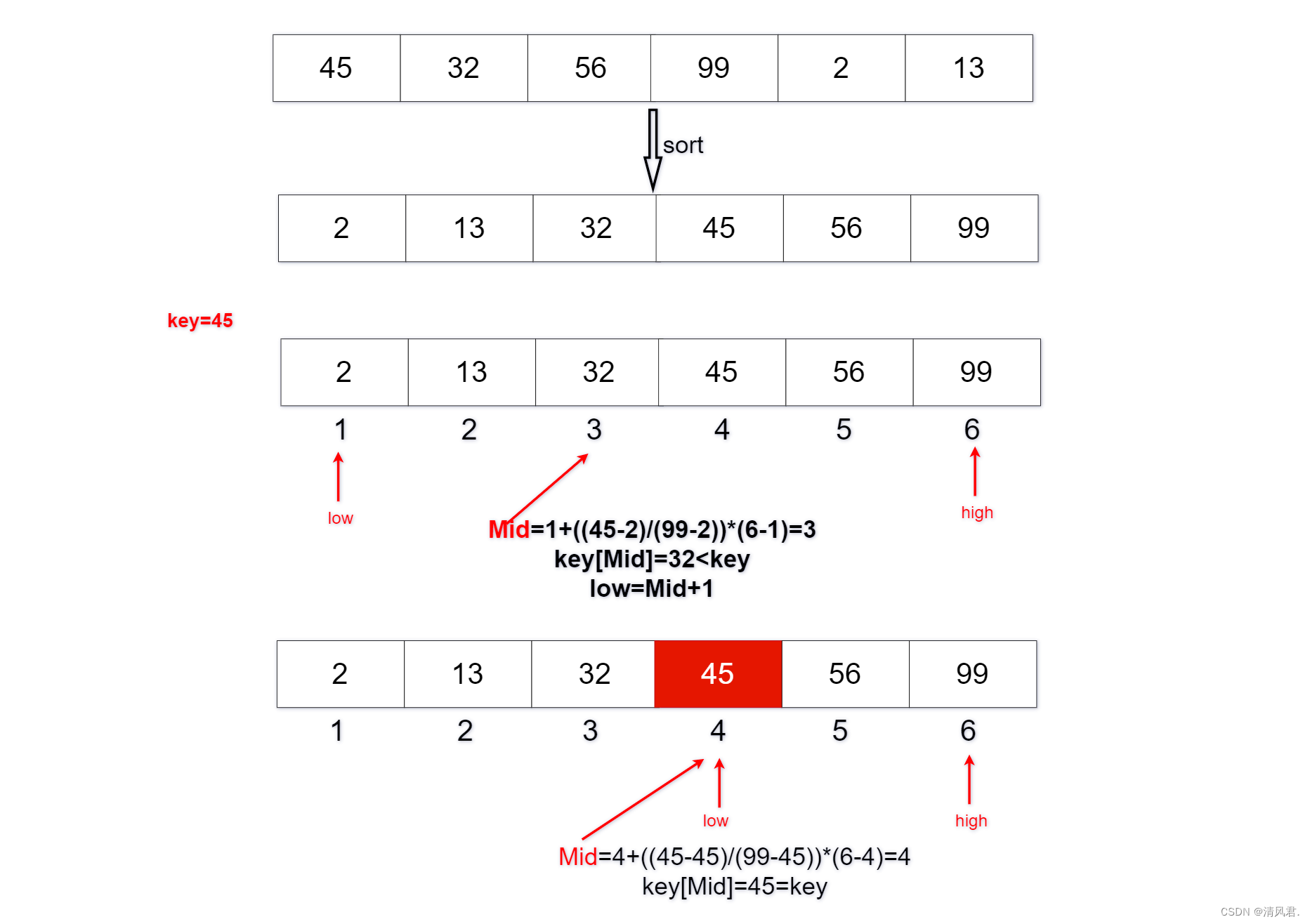
(3)算法分析
①插值查找法优于顺序查找法,如果数据的分布越平均,查找速度就越快,甚至可能第一次就找到数据。插值查找法的时间复杂度取决于数据的分布情况,平均而言优于O(log2^n)。
2.案例实现
①范例程序:用插值查找法去查找10个随机数据中,指定元素数据所在的位置。
②代码展示:
#include<iostream>
using namespace std;
class interpolation_search {
public:int data[10];int val = 0;interpolation_search() {for (int i = 0; i < 10; i++)data[i] = (rand() % 10) + 1;}void sort() {for (int i = 0; i < 10-1; i++){for (int j = i + 1; j < 10; j++){if (data[i] > data[j]){int temp;temp = data[i];data[i] = data[j];data[j] = temp;}}}}void interpolation_search_start() {int low = 0, high = 9;while (low<=high){int mid = low + ((val - data[low]) / (data[high] - data[low])) * (high - low);if (val < data[mid]) {cout << "目标元素在mid的左边" << endl;high = mid - 1;}if (val > data[mid]) {cout << "目标元素在mid的右边" << endl;low = mid + 1;}if (val == data[mid]) {cout << "找到了该元素,该元素位置在" << mid + 1 << "处" << endl;val = 1;break;}}if (val != 1) {cout << "随机生成的数据中没有你要去查找的数据" << endl;}}~interpolation_search() {cout << "随机产生的数据元素如下" << endl;for (int i = 0; i < 10; i++)cout << data[i] << " ";}
};
void text()
{interpolation_search is;is.sort();while (is.val != -1){cout << "请输入你要查找的数:";cin >> is.val;is.interpolation_search_start();}
}
int main()
{text();
}③结果展示:
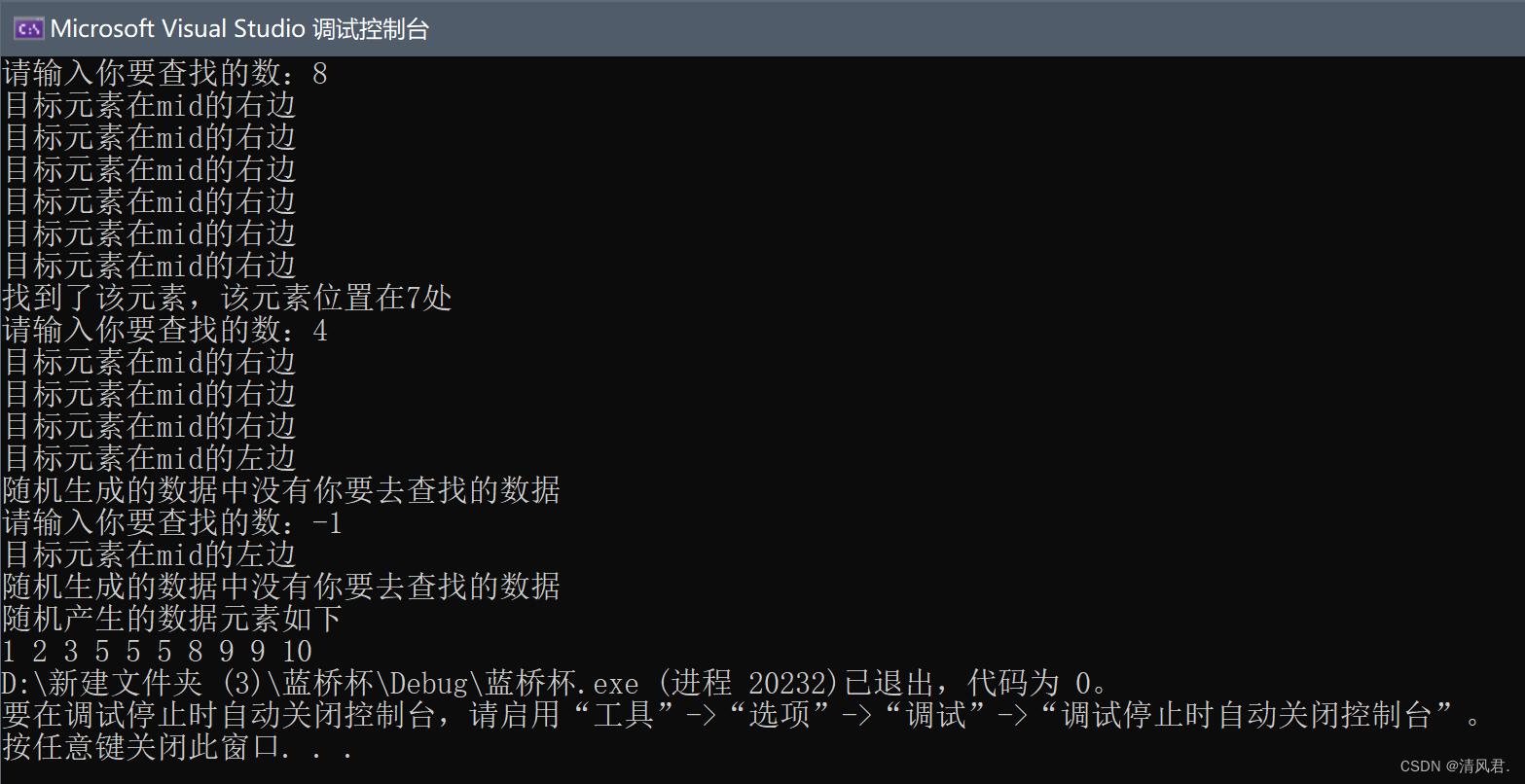
四、斐波那契查找法
1.什么是斐波那契查找法?
(1)简要介绍
斐波那契查找法又被称为斐氏查找法,该方法与二分法一样都是以分割范围来进行查找的,不同的是该方法不是以对半的方式来进行分割的,而是利用斐波那契级数(0、1、1、2、3、5、8、13、21、34、55、...)来进行分割的。该查找法的优点就是只需要用到加减运算,这从计算机运算的底层来看效率是相对较高的。并且该查找法会用到斐波那契树,所以我们应该先来了解该树的基本情况和特点。
(2)具体情况
斐波那契树的建立原则:
①斐波那契树的左右子树都是斐波那契树。
②斐波那契树的树根一定是一个斐波那契数,且子节点与父节点之间的差值的绝对值仍为斐波那契数。
③当k≥2时,斐波那契树的树根为Fib(k),左子树为(k-1)层斐波那契树,右子树为(k-2)层斐波那契树。
④当数据个数n确定时,若想确定斐波那契树的层数k为多少,必须找到一个最小的k值,使斐波那契层数的Fib(k+1)≥n+1。
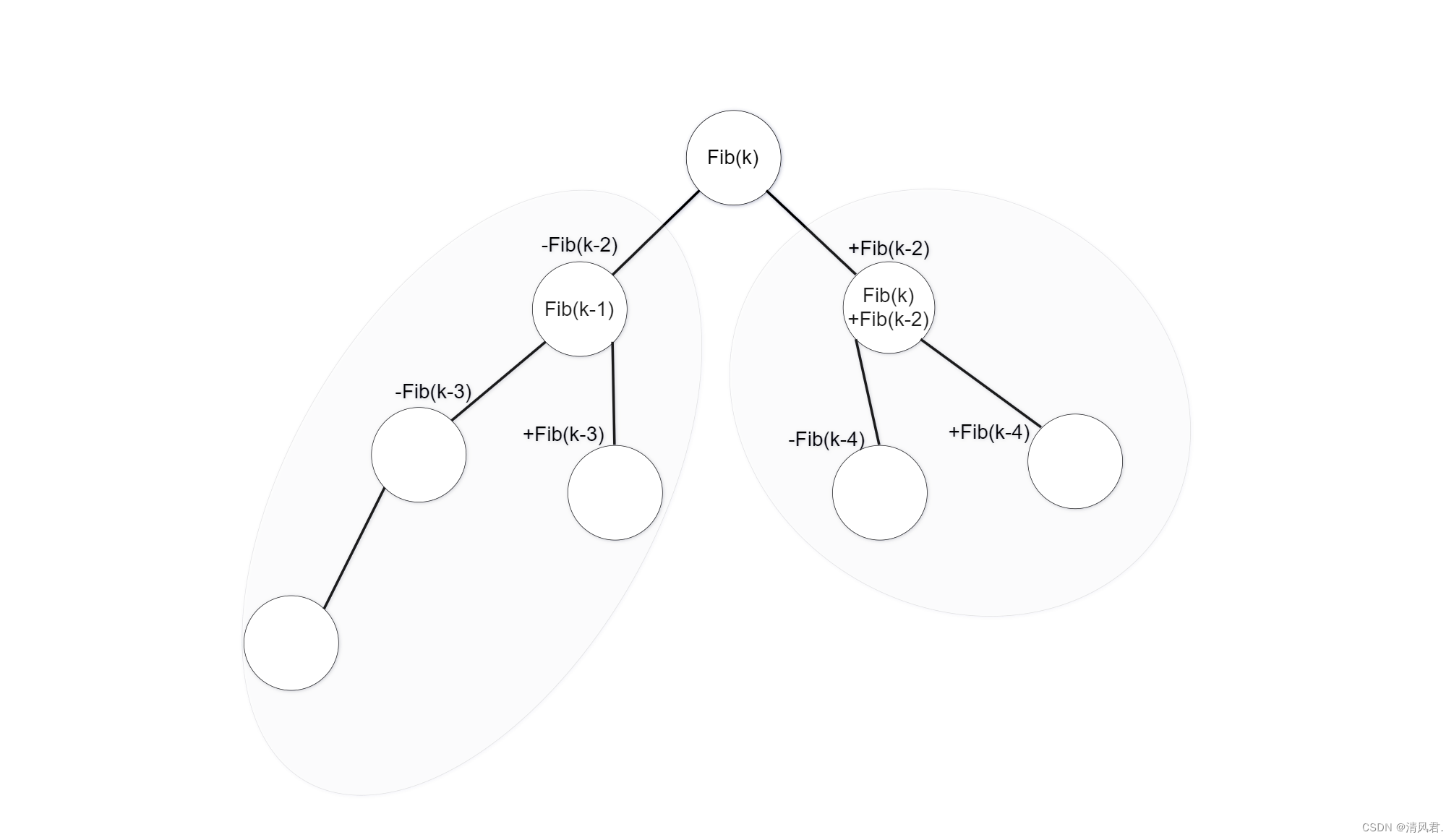
也就是说当数据个数为n,我们找到一个最小的斐波那契数Fib(k+1)使得Fib(k+1)>n+1时,Fib(k)就是这棵树的树根,而Fib(k-2)就是与左右子树开始的差值,左子树去减,右子树去加。例如去求取n=33的斐波那契树。由于n=33,则n+1=34为一棵斐波那契树。由斐波那契公式可得知Fib(0)=0,Fib(1)=1,Fib(2)=1,Fib(3)=2,Fib(4)=3,Fib(5)=5,Fib(6)=8,Fib(7)=13,Fib(8)=21,Fib(9)=34。可知Fib(k+1)≥n+1为Fib(8+1)=34,k=8所以建立二叉树的树根为Fib(8)=21。左子树的树根为Fib(8-1)=13;右子树的树根为Fib(8)+Fib(8-2)=21+8=29;从而依照上述步骤建立的斐波那契树如下图所示:
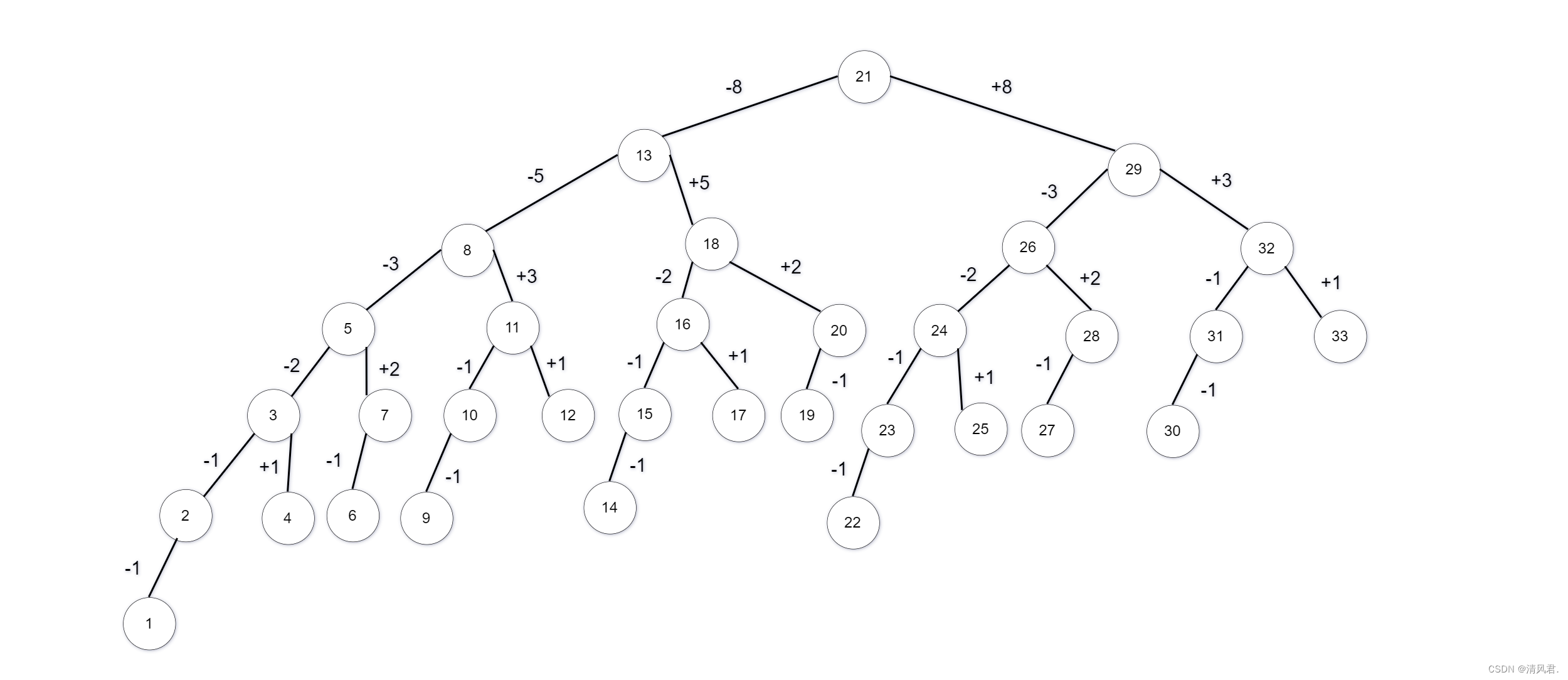
若我们要查找的键值为key,首先要去比较数组下标Fib(k)和键值key,此时就将会出现多种情况如下:
①key值较小,落在了1~Fib(k)-1位置上,所以继续去查找1~Fib(k)-1的数据;key值较大,落在了Fib(k)+1~Fib(k+1)-1的位置上,所以继续去查找Fib(k)+1~Fib(k+1)-1的数据。
②当键值与数组下标Fib(k)的值相等时,则表示成功的查找到了目标数据元素的位置。
(3)算法分析
① 斐波那契查找法虽然平均比较次数少于二分查找法,但在最坏的情况下还是二分查找法较快,并且斐波那契查找法相对复杂,因为它需要去额外产生一棵斐波那契树。
2.案例实现
①范例程序:用斐波那契树查找法去查找指定键值是否存在,并且如果存在其在哪个具体的位置。
②代码展示:
#include<iostream>
using namespace std;
#define size 10
class Fib {
public:int data[size];int val = 0;Fib() {for (int i = 0; i < size; i++)data[i] = (rand() % 10) + 1;}int Fib_start(int n) {if (n == 0 || n == 1)return 1;elsereturn Fib_start(n - 1) + Fib_start(n - 2);}int Fib_search_start() {int index = 2;while (Fib_start(index) <= size)index++;index--;int rootnode = Fib_start(index);int diff_1 = Fib_start(index - 1);int diff_2 = rootnode - diff_1;rootnode--;while (1){if (val == data[rootnode]){return rootnode;}else{if (index == 2)return size;if (val < data[rootnode]){rootnode = rootnode - diff_2;int temp = diff_1;diff_1 = diff_2;diff_2 = temp - diff_2;index = index - 1;}else{if (index == 3)return size;rootnode = rootnode + diff_2;diff_1 = diff_1 - diff_2;diff_2 = diff_2 - diff_1;index = index - 2;}}}}~Fib(){cout << "随机生成的所有数据情况如下" << endl;for (int i = 0; i < 10; i++)cout << data[i] << " ";}
};
void text()
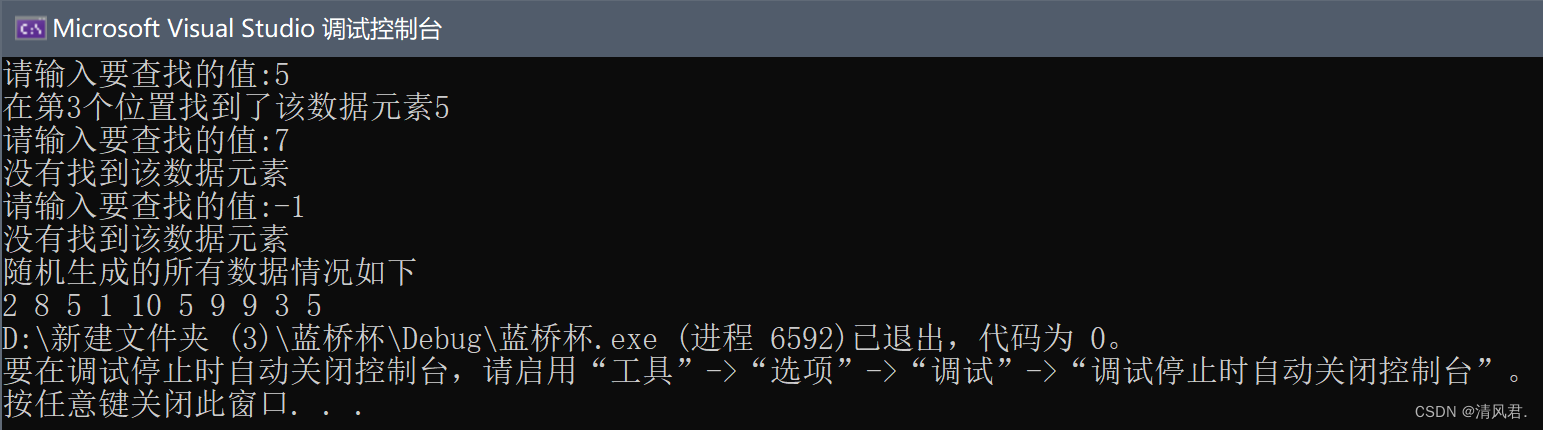
{Fib f;while (f.val != -1){cout << "请输入要查找的值:";cin >> f.val;int count = f.Fib_search_start();if(count==size)cout << "没有找到该数据元素" << endl;elsecout << "在第" << count + 1 << "个位置找到了该数据元素" << f.val << endl;}
}
int main()
{text();
}③结果展示:
总结
以上就是我们对四类查找算法的分析与学习,查找算法在程序设计问题中经常作为一种重要中间的步骤。比如查找数据后,再对数据进行指定步骤的操作行为,所以要在不同的算法题型中合理地运用查找算法,从而达到最高的效率来解决相应的问题。
<您的三连和关注是我最大的动力>
🚀 文章作者:Keanu Zhang 分类专栏:算法之美(C++系列文章)

相关文章:

【查找算法】解析学习四大常用的计算机查找算法 | C++
第二十二章 四大查找算法 目录 第二十二章 四大查找算法 ●前言 ●查找算法 ●一、顺序查找法 1.什么是顺序查找法? 2.案例实现 ●二、二分查找法 1.什么是二分查找法? 2.案例实现 ●三、插值查找法 1.什么是插值查找法? 2…...

Android实例仿真之一
目录 零 开局三问 第一问:为什么要有这一章? 第二问:Android算不算是一个嵌入式系统? 第三问:用什么方法来分析Android这个大系统? 一 讨论Android的流行 二 深入浅出Android 零 开局三问 在正式开始…...
)
软考高级-信息系统管理师之重要工具和技术的口语化表示(最新版)
重要工具和技术的口语化表示 本文主要介绍重要工具和技术的口语化解释 1、 模板、表格和标准:就是用之前的项目的模版、表格、标准,结合本项目进行了修改,在编制一些计划、方案的时候就可以采用这个工具和技术。可以拿来就用的,节约时间、提高质量的。 2、 产品分析:通过一…...
基于springboot+vue的个人健康信息服务平台
基于springbootvue的个人健康信息服务平台 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背…...
SpringBoot2.x实战专题——SpringBoot2 多配置文件【开发环境、测试环境、生产环境】
SpringBoot2.x实战专题——SpringBoot2 多配置文件【开发环境、测试环境、生产环境】 目录SpringBoot2.x实战专题——SpringBoot2 多配置文件【开发环境、测试环境、生产环境】一、创建一个SpringBoot项目二、修改pom.xml中SpringBoot的版本三、配置文件3.1 application-dev.ym…...

测试2:编写测试用例的方法
2.编写测试用例的方法 7种 测试常用的方法:code review 代码静态分析、CI/CD CI–持续集成–开发成员经常集成它们的工作,尽快发现集成错误 CD–持续部署–将集成后的代码部署到更贴近真实运行的环境 2.1 测试用例的描述: 用例编号 用例…...

docker安装配置镜像加速器-拉取创建Mysql容器示例
List item docker 常见命令大全docker安装docker拉取创建Mysql容器docker 安装 1、安装链接:https://blog.csdn.net/BThinker/article/details/123358697 ; 2、安装完成需要配置docker镜像加速器 3、docker 镜像加速器推荐使用阿里云的: 编…...

WSL1和WSL2相互转换以及安装路径迁移相关问题
目录 1.从WSL 1如何切换到WSL 2? 2.从WSL 2如何切换回WSL 1? 3.WSL1转换为WSL2后,WSL1里面安装的程序和库需要重装吗? 4.WSL2转换为WSL1后,WSL2里面安装的程序和库需要重装吗? 5.如何备份WSL2…...

系统分析*
文章目录系统分析分析的任务结构化方法OO的方法的任务常用的详细调查方法有哪些?系统分析的建模TFD业务流程图DFDDD数据流图用例模型(重点用例图)用例图的内容:用例之间的关系:对象模型(类图)时…...

【redis】持久化:RDB和AOF
redis的持久化指将数据写入可靠内存中,如ssd。Redis提供了4种持久化策略 RDB:Redis Database,周期性的将某个时间点的数据集快照持久化AOF:Append Only File,每次redis服务接收到写操作(修改内存的操作),都…...
2023Python接口自动化测试实战教程,附视频实战讲解
这两天一直在找直接用python做接口自动化的方法,在网上也搜了一些博客参考,今天自己动手试了一下。 一、整体结构 上图是项目的目录结构,下面主要介绍下每个目录的作用。 Common:公共方法:主要放置公共的操作的类,比如数据库sql…...
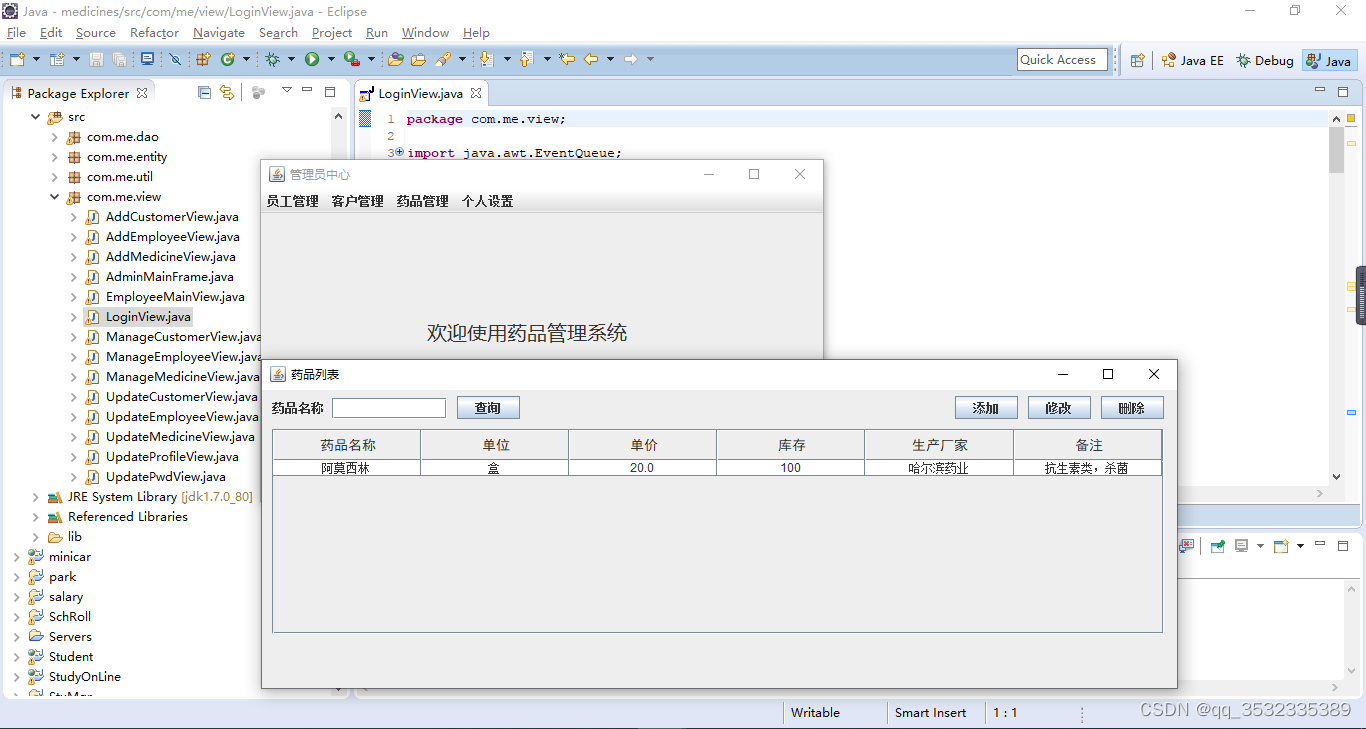
【原创】java+swing+sqlserver药品管理系统设计与实现
之前数据库都是用的mysql,今天我们使用sqlserver在配合swing来开发一个药品管理系统。方便医院工作人员进行药品的管理,基础功能基本都是一些增删改查操作。 功能分析: 药品管理系统主要提供给管理员和员工使用,功能如下&#x…...

软考高级信息系统项目管理师系列之二十七:信息文档管理与配置管理
软考高级信息系统项目管理师系列之二十七:信息文档管理与配置管理 一、信息文档管理与配置管理内容整理二、信息系统文档管理1.信息系统文档概念2.软件文档分类与质量等级三、配置管理1.配置管理2.典型配置项3.配置项4.配置项操作权限5.配置项状态6.配置项版本号7.配置项版本管…...
)
软考高级-信息系统管理师之项目管理基础(最新版)
项目管理基础 项目管理特点战略管理三个过程IT项目特点项目管理概念项目管理特点软技能PRINCE2的四个要素组织结构职能型组织优缺点职能型组织优点同时,职能型组织也存在着如下缺点:项目型组织优缺点项目型组织优点项目型组织也存在着如下缺点:矩阵型组织优缺点矩阵型组织的优…...

leetcode240+Search a 2D Matrix II+从右上角开始
链接 class Solution { public:bool searchMatrix(vector<vector<int>>& matrix, int target) {if(matrix.size()0 || matrix[0].size()0) return false;int i0, jmatrix[0].size()-1; //从右上角开始while (i<matrix.size()&&j>0) {int x mat…...
0xL4ugh 2023
这回跟着个队伍跑,不过还是2X以后的成绩,前边太卷了。自己会的部分,有些是别人已经提交了的。记录一下。Cryptocrypto 1给了一些数据,像这样就没有别的了ct [0, 1, 1, 2, 5, 10, 20, 40, 79, 159, 317, 635, 1269, 2538, 5077, 1…...

Mybatis(4)之跟着老杜做一个简单的银行转账会话
这是个MVC项目,我不一定可以完整的实现这个项目,但力求把这个复现出来,尽量的复现细节。 第一步:创建数据库 表 创建表如下: 我们使用 int 是为了方便 然后采用 demcial,精确度较高 添加两个用户 然后…...

VBA提高篇_ 22 事件处理
文章目录1.事件编程2.常用工作簿事件名称与对应处理过程名称示例3. 事件编程的步骤4.工作簿事件4.1 Open4.2 BeforeClose4.3 NewSheet5.工作表事件6.变量和过程函数的作用域1.事件编程 写在事件发生地(对应工作簿或工作表) 2.常用工作簿事…...

【蓝桥杯集训·周赛】AcWing 第91场周赛
文章目录第一题 AcWing 4861. 构造数列一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第二题 AcWing 4862. 浇花一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第三题 AcWing 4861. 构造数列一、题目1、原题…...
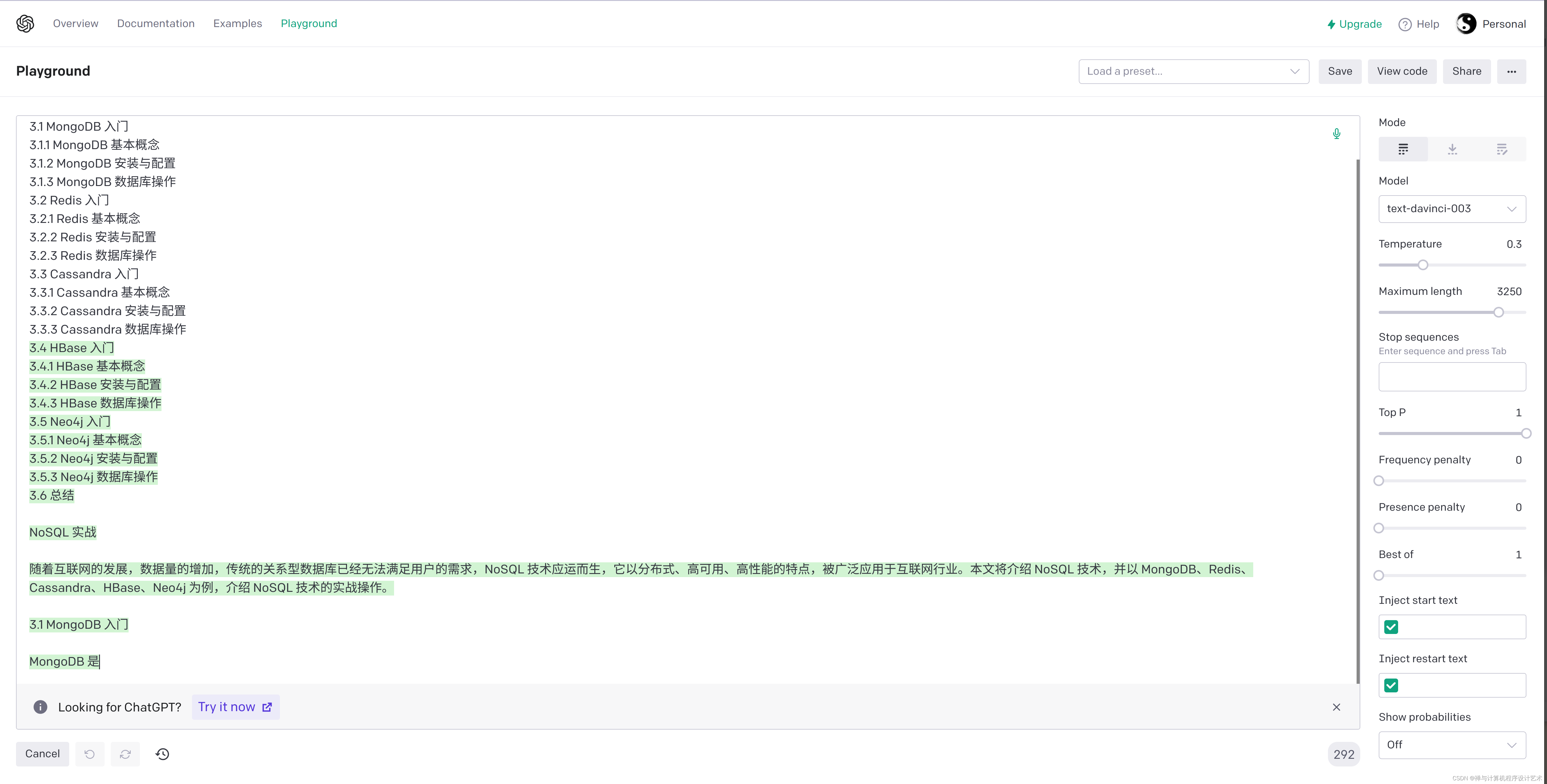
【人工智能AI】三、NoSQL 实战《NoSQL 企业级基础入门与进阶实战》
帮我写一篇介绍NoSQL的技术文章,文章标题是《NoSQL 实战》,不少于3000字。这篇文章的目录是 3.NoSQL 实战 3.1 MongoDB 入门 3.1.1 MongoDB 基本概念 3.1.2 MongoDB 安装与配置 3.1.3 MongoDB 数据库操作 3.2 Redis 入门 3.2.1 Redis 基本概念 3.2.2 Red…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...

