算法|Day45 动态规划13
LeetCode 300.最长递增子序列
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
题目描述:给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
解题思路
通过两次循环,在j<i时判断nums[j]是否小于nums[i],如果是则子序列长度加一
- 确定dp数组(dp table)以及下标的含义
dp[i]代表从0到i递增子序列的长度
- 确定递推公式
if(nums[i] > nums[j]) dp[i] = max(dp[i],dp[j]+1);
- dp数组如何初始化
一个数就是长度为1的子序列,所以全部初始化为1.
- 确定遍历顺序
从递归公式其实已经可以看出,一定是从前向后遍历,因为dp[i],依靠dp[i - 1]的数值。
- 举例推导dp数组
class Solution {
public:int lengthOfLIS(vector<int>& nums) {if(nums.size() == 1) return 1;vector<int> dp(nums.size(),1);int result = 0;for(int i=1;i<nums.size();i++){for(int j=0;j<i;j++){if(nums[i] > nums[j]){dp[i] = max(dp[i],dp[j]+1);}result = max(result,dp[i]);}}return result;}
};总结:
- 子序列要二重遍历。
LeetCode 674.最长连续递增序列
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
题目描述:给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
解题思路
- 确定dp数组(dp table)以及下标的含义
dp[i]代表到nums[i]为止,最长的连续递增子序列
- 确定递推公式
如果前一个前一个数小于后一个数,也就是递增的,我们就将当前dp+1,如果不小于,就不操作,也就是将其置1,初始化时已经置1,所以不用操作。
if(nums[i] > nums[i-1]) dp[i] = dp[i-1]+1;
- dp数组如何初始化
全部初始化为1
- 确定遍历顺序
正序遍历即可
- 举例推导dp数组
class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {vector<int> dp(nums.size(),1);int result = 1;for(int i=1;i<nums.size();i++){if(nums[i] > nums[i-1]){dp[i] = dp[i-1]+1;}result = max(result,dp[i]);}return result;}
};总结:
- 较为简单
LeetCode 718.最长重复子数组
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
题目描述:给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
解题思路
- 确定dp数组(dp table)以及下标的含义
dp[i][j] :以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j]。 (特别注意: “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 )
- 确定递推公式
即当A[i - 1] 和B[j - 1]相等的时候,dp[i][j] = dp[i - 1][j - 1] + 1;
不相等就是0了,也就不用操作
- dp数组如何初始化
全部初始化为0
- 确定遍历顺序
先遍历数组1,或者数组2都可以。
- 举例推导dp数组
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size()+1,vector<int>(nums2.size()+1,0));int result = 0;for(int i=1;i<=nums1.size();i++){for(int j=1;j<=nums2.size();j++){if(nums1[i-1] == nums2[j-1]){dp[i][j] = dp[i-1][j-1]+1;}result = max(result,dp[i][j]);}}return result;}
};总结:
- 本来以为是要搞几个状态,没想到直接用二维来代表俩数组遍历的情况了。
相关文章:

算法|Day45 动态规划13
LeetCode 300.最长递增子序列 题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目描述:给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除&…...

基于随机森林的手写体数字识别,基于RF的手写体数字识别,基于RF的MNIST数据集分类识别
目录 背影 摘要 随机森林的基本定义 随机森林实现的步骤 基于随机森林的MNIST数据集分类识别 代码下载链接: 随机森林的手写体数字分类识别,随机森林的MNIST手写体数据集分类识别,卷积神经网络的手写体数字识别(代码完整,数据完整)资源-CSDN文库 https://download.csdn.n…...

vite初始化vue3项目(配置自动格式化工具与git提交规范工具)
初始化项目 vite构建vue项目还是比较简单的,简单配置选择一下就行了 初始化命令 npm init vuelatest初始化最新版本vue项目 2. 基本选项含义 Add TypeScript 是否添加TSADD JSX是否支持JSXADD Vue Router是否添加Vue Router路由管理工具ADD Pinia 是否添加pinia…...

leetcode473. 火柴拼正方形(回溯算法-java)
火柴拼正方形 leetcode473 火柴拼正方形题目描述回溯算法 上期经典算法 leetcode473 火柴拼正方形 难度 - 中等 原题链接 - leetcode473 火柴拼正方形 题目描述 你将得到一个整数数组 matchsticks ,其中 matchsticks[i] 是第 i 个火柴棒的长度。你要用 所有的火柴棍…...

git-fatal: No url found for submodule path ‘packages/libary‘ in .gitmodules
文章目录 前言一、git submodule功能使用二、错误信息:三、解决方法:四、.gitmodules配置文件:总结 前言 最近在做vue项目,因为项目比较复杂,把功能拆分成很多子模块,我们使用Git的submodule功能。遇到错误…...

Android开发之性能优化:过渡绘制解决方案
1. 过渡绘制 屏幕上某一像素点在一帧中被重复绘制多次,就是过渡绘制。 下图中多个卡片跌在一起,但是只有第一个卡片是完全可见的。背后的卡片只有部分可见。但是Android系统在绘制时会将下层的卡片进行绘制,接着再将上层的卡片进行绘制。但其…...

Wireshark 抓包过滤命令汇总
Wireshark 抓包过滤命令汇总 Wireshark 是一个强大的网络分析工具,它可以帮助网络管理员和安全专家监控和分析网络流量。通过捕获网络数据包,Wireshark 能够帮助我们识别网络中的问题、瓶颈以及潜在的安全威胁。在使用 Wireshark 进行网络数据包分析时&…...

配资平台app(正规股票配资软件)架构是怎么搭建的?
随着股票市场的发展,越来越多的投资者开始尝试使用股票配资平台进行杠杆炒股,因此,搭建一套稳定、可靠的配资平台app架构显得尤为重要。本文将介绍配资平台app架构设计的关键要素,以及建立一个正规的配资平台app所需考虑的问题。 …...

【实用黑科技】如何 把b站的缓存视频弄到本地——数据恢复软件WinHex 和 音视频转码程序FFmpeg
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:效率…...

神经网络基础-神经网络补充概念-57-多任务学习
概念 多任务学习(Multi-Task Learning,MTL)是一种机器学习方法,旨在同时学习多个相关任务,通过共享特征表示来提高模型的性能。在多任务学习中,不同任务之间可以是相关的,共享的,或…...
CMake教程6:调用lib、dll
之前我们学到了如何编写一个可执行程序和Library,在继续学习之前,需要解释下target,在cmake中我们可以给executable和library设置一个target名字,这样可以方便我们在后续对target进行更加详细的属性设置。 本节我们将学习如何在项…...

行业资讯丨“燃气智慧化”到底是什么?
文章来源:网络 关键词:智慧燃气、智慧燃气场站、设备设施数字化、数字孪生、工业互联网 带你了解燃气信息化 随着科技的不断进步和信息化的快速发展,各行各业都在积极探索如何将技术应用于业务中,以提高效率和服务质量。 燃气…...

angular注入方法providers
在Angular中有很多方式可以将服务类注册到注入器中: Injectable 元数据中的providedIn属性 NgModule 元数据中的 providers属性 Component 元数据中的 providers属性 创建一个文件名叫名 hero.service.ts叫 hero 的服务 hero.service.ts import { Injectable } from angular…...

Git提交规范指南
在开发过程中,Git每次提交代码,都需要写Commit message(提交说明),规范的Commit message有很多好处: 方便快速浏览查找,回溯之前的工作内容可以直接从commit 生成Change log(发布时用于说明版本…...
QT之UDP通信
QT之UDP通信 UDP不分客户端口服务器,只需要使用一个类QUdpSocket QT += core gui networkgreaterThan(QT_MAJOR_VERSION, 4): QT += widgetsTARGET = udp TEMPLATE = app# The following define makes your compiler emit warnings if you use # any feature of Qt …...
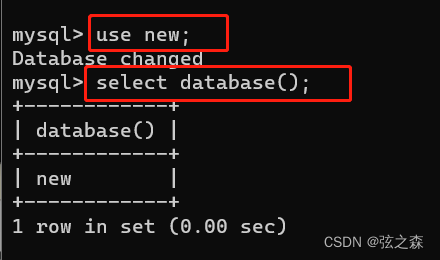
一、进入sql环境,以及sql的查询、新建、删除、使用
1、进入sql环境 》》》mysql -u root -p 》》》输入密码 2、sql语言的分类 3、注意事项: 4、基础操作: (1)查询所有数据库: show databases; 运行结果: (2)创建一个新的数据库&…...
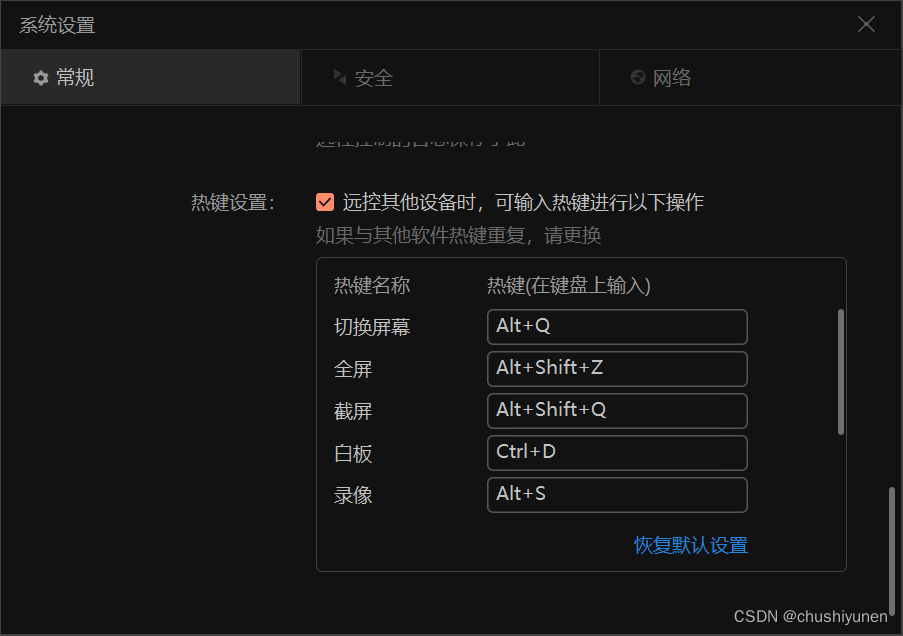
向日葵如何截图
场景 向日葵远程时,有时需要截图,但是客户电脑上没有qq、微信等软件提供快捷截图。 怎么办呢? 解决方案 其实向日葵肯定支持这些功能的。 设置 | 热键设置 | 勾选 远控其他设备时,可输入热键进行以下操作。 如果: altq 切换…...

固定资产折旧报表
SELECT * FROM SYS_ORGANIZATION -- OID、OCODE、ONAME、OATTRIBUT、FPC_USE_UNITNAME -- IS_DELETE 0 STATUS 1 SELECT * FROM FA_PROPERTY_CARD -- FPC_MANAGE_UNIT、FPC_ZJLY、FPC_ZJLYNAME、FPC_RESOURCE、FPC_MON_ZJE、FPC_SUMZJ、FPC_J…...

ubuntu18 下更改 mysql 数据目录
一、修改步骤 更改 MySQL 的数据目录需要注意以下几个步骤: 停止 MySQL 服务 在 Ubuntu 中,你可以使用以下命令停止 MySQL 服务: sudo systemctl stop mysql 复制现有数据 假设你的新的数据目录是 /new/dir/mysql,你应该使用 rsy…...

Arduino看门狗定时器WDT
Arduino - 看门狗定时器(WDT:Watch Dog Timer) 参考 看门狗定时器(WDT:Watch Dog Timer)实际上是一个计数器。 一般给看门狗一个大数,程序开始运行后看门狗开始倒计数。 如果程序运行正常&…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
