未出现过的最小正整数
给定一个长度为 n
的整数数组,请你找出未在数组中出现过的最小正整数。
样例
输入1:[-5, 3, 2, 3]输出1:1输入2:[1, 2, 3]输出2:4
数据范围
1≤n≤105
,
数组中元素的取值范围 [−109,109]。
代码:
class Solution {
public:int findMissMin(vector<int>& nums) {int n=nums.size();vector<bool> hash(n+1);for(int x:nums){if(x>=1&&x<=n)hash[x]=true;}for(int i=1;i<=n;i++){if(!hash[i]){return i;}}return n+1;}
};相关文章:

未出现过的最小正整数
给定一个长度为 n 的整数数组,请你找出未在数组中出现过的最小正整数。 样例 输入1:[-5, 3, 2, 3]输出1:1输入2:[1, 2, 3]输出2:4数据范围 1≤n≤105 , 数组中元素的取值范围 [−109,109]。 代码: c…...

易服客工作室:WordPress是什么?初学者的解释
目录 什么是WordPress? WordPress可以制作什么类型的网站? 谁制作了WordPress?它已经存在多久了? 谁使用 WordPress? 白宫网站 微软 滚石乐队 为什么要使用 WordPress? WordPress 是免费且…...
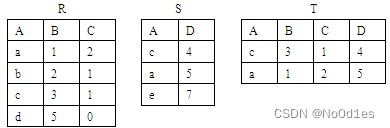
2019年9月全国计算机等级考试真题(C语言二级)
2019年9月全国计算机等级考试真题(C语言二级) 第1题 1、“商品”与“顾客”两个实体集之间的联系一般是 A. 一对一 B. 一对多 C. 多对一 D. 多对多 正确答案:D 第2题 定义学生选修课程的关系模式:SC(S#,…...

LLaMA模型泄露 Meta成最大受益者
一份被意外泄露的谷歌内部文件,将Meta的LLaMA大模型“非故意开源”事件再次推到大众面前。“泄密文件”的作者据悉是谷歌内部的一位研究员,他大胆指出,开源力量正在填平OpenAI与谷歌等大模型巨头们数年来筑起的护城河,而最大的受益…...
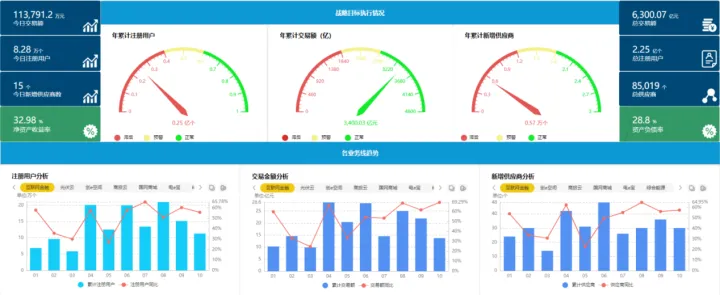
企业中商业智能BI,常见的工具和技术
商业智能(Business Intelligence,简称BI)数据可视化是通过使用图表、图形和其他可视化工具来呈现和解释商业数据的过程。它旨在帮助组织更好地理解和分析他们的数据,从而做出更明智的商业决策。 常见的商业智能数据可视化工具和技…...
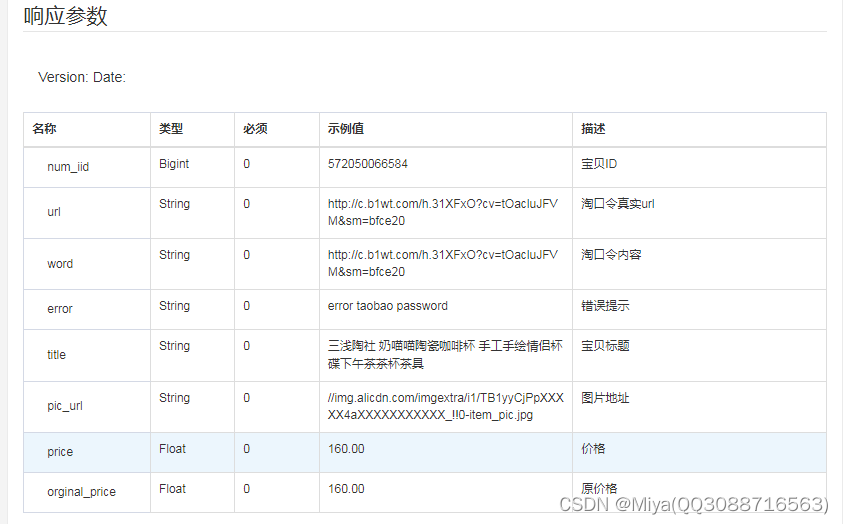
item_password-获得淘口令真实url
一、接口参数说明: item_password-获得淘口令真实url ,点击更多API调试,请移步注册API账号点击获取测试key和secret 公共参数 请求地址: https://api-gw.onebound.cn/taobao/item_password 名称类型必须描述keyString是调用key(…...
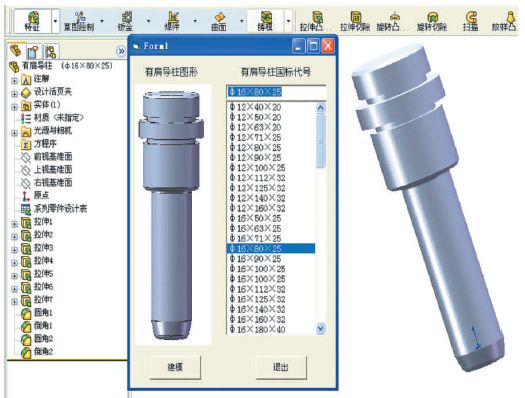
基于SOLIDWORKS配置功能建立塑料模具标准件库
在塑料模具的设计过程中,建立其三维模型对于后续进行CAE分析和CAM加工是非常重要的。除了型腔和型芯以外,塑料模具中的标准件很多,如推杆、导柱、导套、推板、限位钉等,这些对于不同的产品是需要反复调用的。目前,我国…...
1.物联网LWIP网络,TCP/IP协议簇
一。TCP/IP协议簇 1.应用层:FTP,HTTP,Telent,DNS,RIP 2.传输层:TCP,UDP 3.网络层:IPV4,IPV6,OSPF,EIGRP 4.数据链路层:Ethernet&#…...

拷贝公钥文件后,ssh 服务器仍提示输入密码
我们因为工作需要,可能在本地包含多个公私钥对,且每个公私钥对在生成时,指定的邮箱也不相同,所以我们在登录一些机器时,会指定不同的公钥文件,但是,有时候就算我们指定了正确的公钥文件…...
算法|Day45 动态规划13
LeetCode 300.最长递增子序列 题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目描述:给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除&…...

基于随机森林的手写体数字识别,基于RF的手写体数字识别,基于RF的MNIST数据集分类识别
目录 背影 摘要 随机森林的基本定义 随机森林实现的步骤 基于随机森林的MNIST数据集分类识别 代码下载链接: 随机森林的手写体数字分类识别,随机森林的MNIST手写体数据集分类识别,卷积神经网络的手写体数字识别(代码完整,数据完整)资源-CSDN文库 https://download.csdn.n…...

vite初始化vue3项目(配置自动格式化工具与git提交规范工具)
初始化项目 vite构建vue项目还是比较简单的,简单配置选择一下就行了 初始化命令 npm init vuelatest初始化最新版本vue项目 2. 基本选项含义 Add TypeScript 是否添加TSADD JSX是否支持JSXADD Vue Router是否添加Vue Router路由管理工具ADD Pinia 是否添加pinia…...

leetcode473. 火柴拼正方形(回溯算法-java)
火柴拼正方形 leetcode473 火柴拼正方形题目描述回溯算法 上期经典算法 leetcode473 火柴拼正方形 难度 - 中等 原题链接 - leetcode473 火柴拼正方形 题目描述 你将得到一个整数数组 matchsticks ,其中 matchsticks[i] 是第 i 个火柴棒的长度。你要用 所有的火柴棍…...

git-fatal: No url found for submodule path ‘packages/libary‘ in .gitmodules
文章目录 前言一、git submodule功能使用二、错误信息:三、解决方法:四、.gitmodules配置文件:总结 前言 最近在做vue项目,因为项目比较复杂,把功能拆分成很多子模块,我们使用Git的submodule功能。遇到错误…...

Android开发之性能优化:过渡绘制解决方案
1. 过渡绘制 屏幕上某一像素点在一帧中被重复绘制多次,就是过渡绘制。 下图中多个卡片跌在一起,但是只有第一个卡片是完全可见的。背后的卡片只有部分可见。但是Android系统在绘制时会将下层的卡片进行绘制,接着再将上层的卡片进行绘制。但其…...

Wireshark 抓包过滤命令汇总
Wireshark 抓包过滤命令汇总 Wireshark 是一个强大的网络分析工具,它可以帮助网络管理员和安全专家监控和分析网络流量。通过捕获网络数据包,Wireshark 能够帮助我们识别网络中的问题、瓶颈以及潜在的安全威胁。在使用 Wireshark 进行网络数据包分析时&…...

配资平台app(正规股票配资软件)架构是怎么搭建的?
随着股票市场的发展,越来越多的投资者开始尝试使用股票配资平台进行杠杆炒股,因此,搭建一套稳定、可靠的配资平台app架构显得尤为重要。本文将介绍配资平台app架构设计的关键要素,以及建立一个正规的配资平台app所需考虑的问题。 …...

【实用黑科技】如何 把b站的缓存视频弄到本地——数据恢复软件WinHex 和 音视频转码程序FFmpeg
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:效率…...

神经网络基础-神经网络补充概念-57-多任务学习
概念 多任务学习(Multi-Task Learning,MTL)是一种机器学习方法,旨在同时学习多个相关任务,通过共享特征表示来提高模型的性能。在多任务学习中,不同任务之间可以是相关的,共享的,或…...
CMake教程6:调用lib、dll
之前我们学到了如何编写一个可执行程序和Library,在继续学习之前,需要解释下target,在cmake中我们可以给executable和library设置一个target名字,这样可以方便我们在后续对target进行更加详细的属性设置。 本节我们将学习如何在项…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...
