算法|Day42 动态规划10
LeetCode 121.买卖股票的最佳时机
题目链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/description/
题目描述:给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
解题思路
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:一个二维的dp数组,第一维表示天数,第二维表示是否持有股票。第二维0表示持有,1表示不持有。dp[i][j]表示dp[i][1] 表示第i天不持有股票所得最多现金
- 确定递推公式
如果第i天持有股票即dp[i][0]
- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
- 第i天买入股票,所得现金就是买入今天的股票后所得现金即:-prices[i]
如果第i天不持有股票即dp[i][1]
- 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
- 第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:prices[i] + dp[i - 1][0]
我们取最大值即可,即
dp[i][0] = max(dp[i-1][0],-prices[i]);
dp[i][1] = max(dp[i-1][1],dp[i-1][0]+prices[i]);
- dp数组如何初始化
那么dp[0][0]表示第0天持有股票,此时的持有股票就一定是买入股票了,因为不可能有前一天推出来,所以dp[0][0] -= prices[0];
dp[0][1]表示第0天不持有股票,不持有股票那么现金就是0,所以dp[0][1] = 0;
- 确定遍历顺序
正序遍历即可
- 举例推导dp数组
class Solution {
public:int maxProfit(vector<int>& prices) {int len = prices.size();if(len == 1) return 0;vector<vector<int>> dp(len,vector<int>(2));dp[0][0] = -prices[0];dp[0][1] = 0;for(int i=1;i<len;i++){dp[i][0] = max(dp[i-1][0],-prices[i]);dp[i][1] = max(dp[i-1][1],dp[i-1][0]+prices[i]);}return dp[len-1][1];}
};总结:
- 状态多时可以尝试多维数组来表示,只能买卖一次所以这题要么是-prices(i)要么就是前一次的情况。
LeetCode 122.买卖股票的最佳时机 II
题目链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/description/
题目描述:给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
解题思路
本题和上题的唯一区别就是可以买卖多次
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:一个二维的dp数组,第一维表示天数,第二维表示是否持有股票。第二维0表示持有,1表示不持有。dp[i][j]表示dp[i][1] 表示第i天不持有股票所得最多现金
- 确定递推公式
和上一题几乎一样,除了这里可以反复卖,要么我们是今天买了,要么就是保持前一天买的状态,取最大值即可。
- dp数组如何初始化
那么dp[0][0]表示第0天持有股票,此时的持有股票就一定是买入股票了,因为不可能有前一天推出来,所以dp[0][0] -= prices[0];
dp[0][1]表示第0天不持有股票,不持有股票那么现金就是0,所以dp[0][1] = 0;
- 确定遍历顺序
正序遍历即可
- 举例推导dp数组
class Solution {
public:int maxProfit(vector<int>& prices) {int len = prices.size();vector<vector<int>> dp(len, vector<int>(2, 0));dp[0][0] -= prices[0];dp[0][1] = 0;for (int i = 1; i < len; i++) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); // 注意这里是和121. 买卖股票的最佳时机唯一不同的地方。dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);}return dp[len - 1][1];}
};总结:
- 环的情况,只需要列举出第一个房子和最后一个房子的情况,并分情况讨论即可。本来还以为需要统一处理。
相关文章:

算法|Day42 动态规划10
LeetCode 121.买卖股票的最佳时机 题目链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/description/ 题目描述:给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天…...
vmalert集成钉钉告警
vmalert通过在alert.rules中配置告警规则实现告警,告警规则语法与Prometheus兼容,依赖Alertmanager与prometheus-webhook-dingtalk实现钉钉告警,以下步骤: 1、构建vmalert 从源代码构建vmalert: git clone https://…...

深入解析 MyBatis 中的 <foreach> 标签:优雅处理批量操作与动态 SQL
在当今的Java应用程序开发中,数据库操作是一个不可或缺的部分。MyBatis作为一款颇受欢迎的持久层框架,为我们提供了一种优雅而高效的方式来管理数据库操作。在MyBatis的众多特性中,<foreach>标签无疑是一个强大的工具,它使得…...
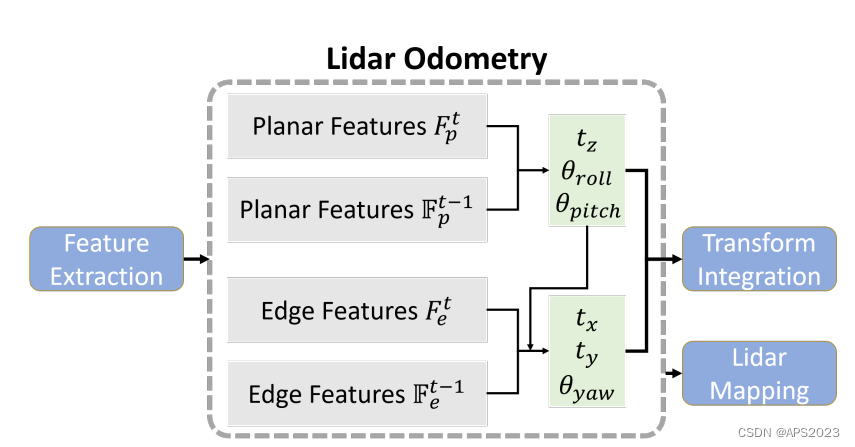
LeGO-Loam代码解析(二)--- Lego-LOAM的地面点分离、聚类、两步优化方法
1 地面点分离剔除方法 1.1 数学推导 LeGO-LOAM 中前端改进中很重要的一点就是充分利用了地面点,那首先自然是提取 对地面点的提取。 如上图,相邻的两个扫描线束的同一列打在地面上如 点所示,他们的垂直高度差 ,水平距离差 ,计算垂直高度差和水平高度差…...

程序员如何利用公网打造低成本轻量化的搜索和下载平台【内网穿透】
🎬 鸽芷咕:个人主页 🔥 个人专栏: 《高效编程技巧》《cpolar》 ⛺️生活的理想,就是为了理想的生活! 公网远程访问本地硬盘文件【内网穿透】 文章目录 公网远程访问本地硬盘文件【内网穿透】前言1. 下载cpolar和Everything软件1.…...
构建可远程访问的企业内部论坛
文章目录 前言1.cpolar、PHPStudy2.Discuz3.打开PHPStudy,安装网页论坛所需软件4.进行网页运行环境的构建5.运行Discuz网页程序6.使用cpolar建立穿透内网的数据隧道,发布到公网7.对云端保留的空白数据隧道进行配置8.Discuz论坛搭建完毕 前言 企业在发展…...
场:河南理工大学-C 旅游)
2023河南萌新联赛第(六)场:河南理工大学-C 旅游
2023河南萌新联赛第(六)场:河南理工大学 https://ac.nowcoder.com/acm/contest/63602/C 文章目录 2023河南萌新联赛第(六)场:河南理工大学题意解题思路代码 题意 小C喜欢旅游,现在他要去DSH旅…...
)
C语言 常用工具型API ----------strchr()
函数原型 char *strchr(const char *str, int c) 参数 str-- 要被检索的 C 字符串。 c-- 在 str 中要搜索的字符。 功能 在参数str所指向的字符串中搜索第一次出现字符c(一个无符号字符)的位置 头文件 #include <string.h> 返回值 返回一…...

建造者模式的理论与实现
本文实践代码仓库:https://github.com/goSilver/my_practice 文章目录 一、定义二、作用三、实现四、总结 一、定义 建造者模式是一种创建复杂对象的设计模式。它将一个复杂对象的构建过程分解为多个简单的步骤,并且允许按照特定的顺序来构建对象。通过…...

非计算机科班如何顺利转码进入计算机领域?
文章目录 如何规划才能实现转码?计算机岗位发展前景?现阶段转码 总结 🎉欢迎来到Java学习路线专栏~探索非计算机科班如何顺利转码进入计算机领域 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页:IT陈寒的博客dz…...
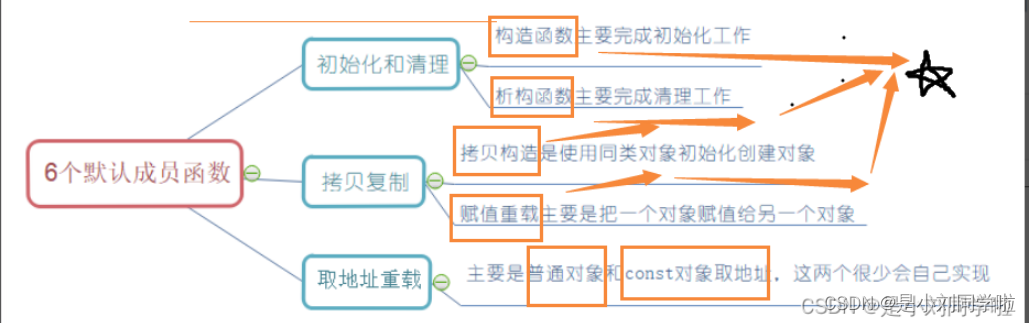
【C++类和对象】类有哪些默认成员函数呢?(下)
文章目录 一、类的6个默认成员函数二、日期类的实现2.1 运算符重载部分2.2 日期之间的运算2.3 整体代码1.Date.h部分2. Date.cpp部分 三. const成员函数四. 取地址及const取地址操作符重载扩展内容 总结 ヾ(๑╹◡╹)ノ" 人总要为过去的懒惰而付出代价ヾ(๑╹◡…...

springboot自定义banner的输出与源码解析
文章目录 一、介绍二、演示环境三、自定义banner1. 文本2. 图片3. placeholder占位符4. 关闭banner 四、源码分析1. 关闭banner2. banner模式3. banner打印器4. 打印banner① 获取banner② 打印banner 5. 版本号占位符的解析器6. 文本格式占位符的解析器7. 应用标题占位符的解析…...

LeetCode 141.环形链表
文章目录 💡题目分析💡解题思路🔔接口源码💡深度思考❓思考1❓思考2 题目链接👉 LeetCode 141.环形链表👈 💡题目分析 给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中…...
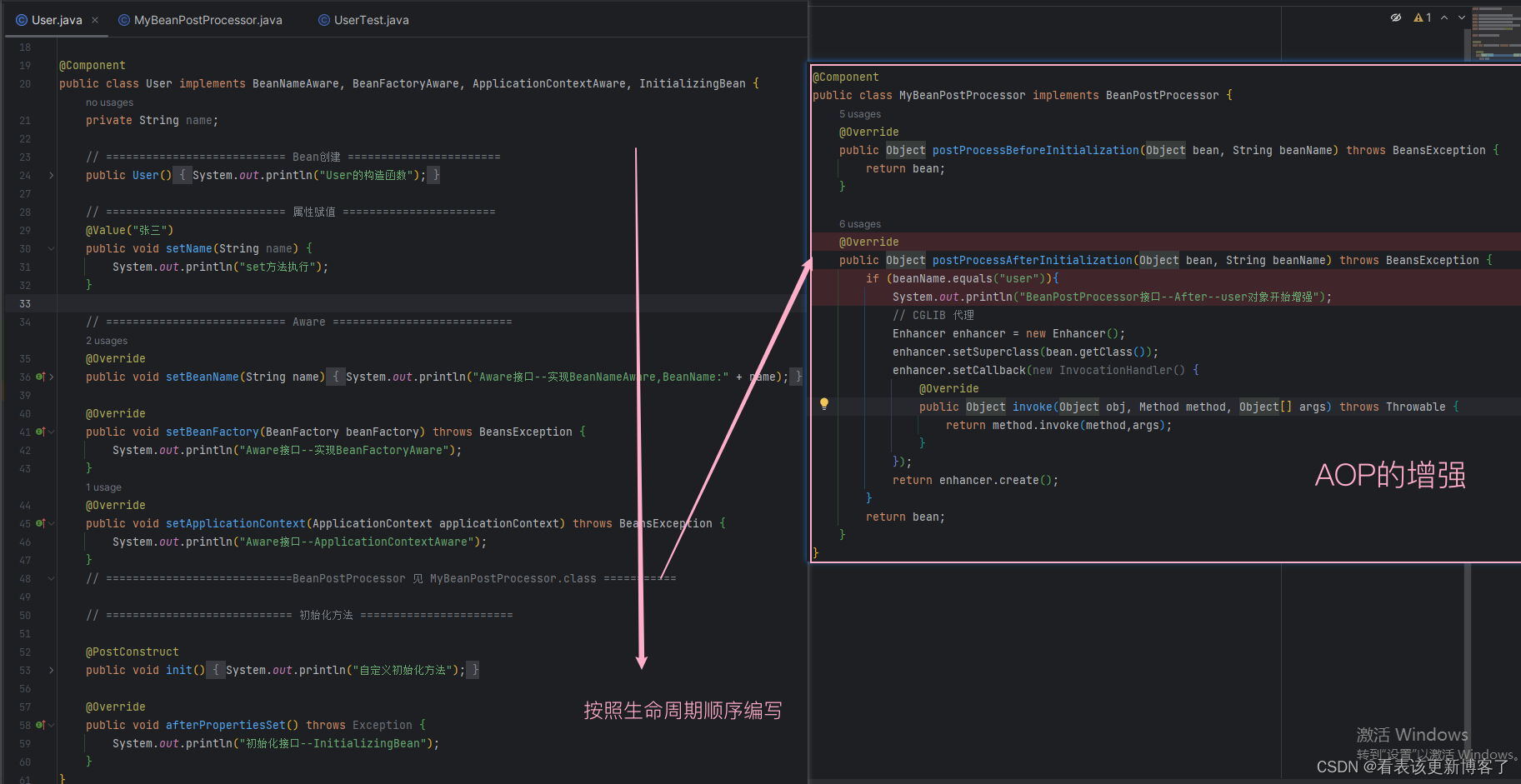
Spring-Bean的生命周期
目录 生命周期汇总 细分生命周期 1.实例化 2.属性赋值(依赖注入) 3.Aware接口 4.BeanPostProcessor接口 5.初始化 6.销毁 测试验证 类结构 业务类 测试类 生命周期汇总 Spring Bean 的生命周期见下图 (一定记忆好下图&#x…...
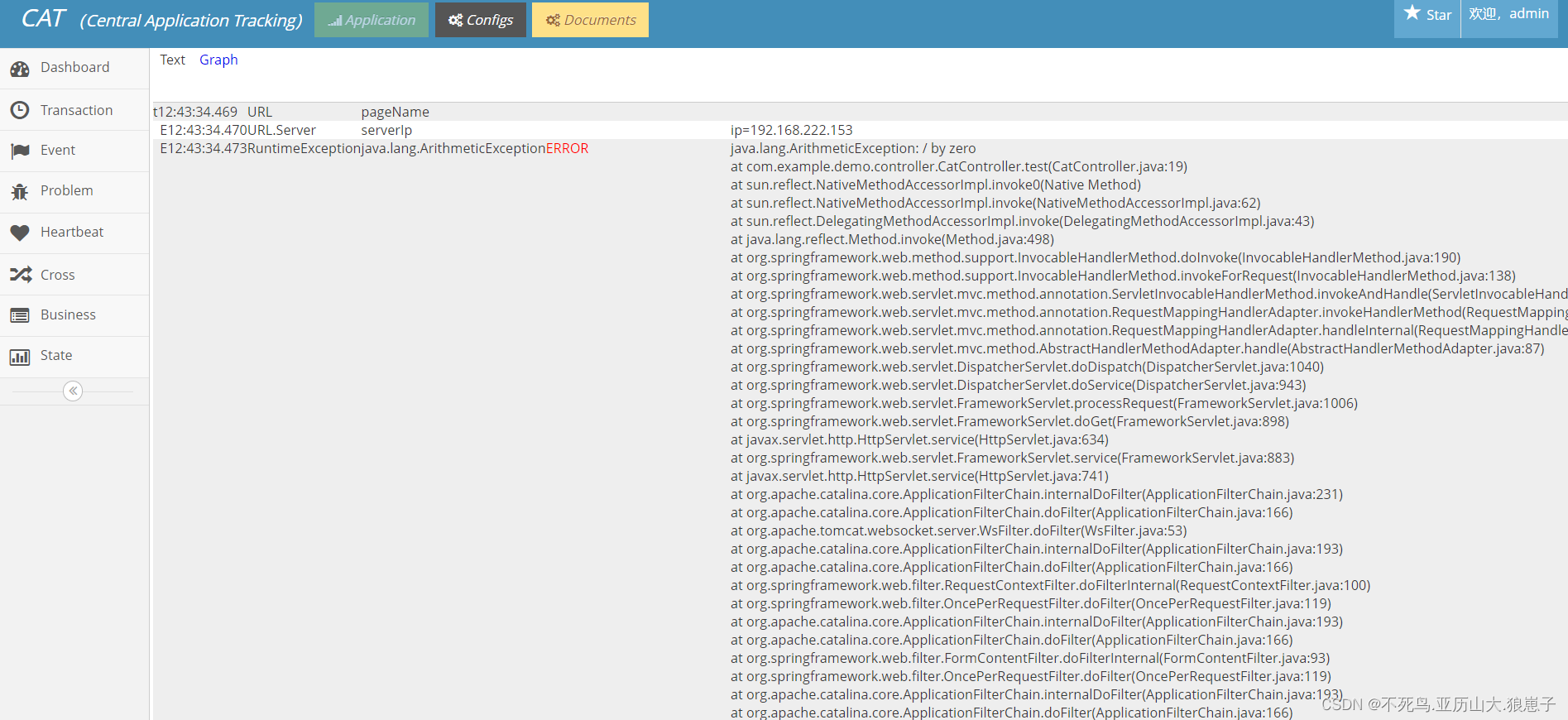
Cat(3):客户端集成—简单案例
接下来编写一个简单的springboot与Cat整合的案例 1 新建springboot项目 首先创建一个Spring Boot的初始化工程。只需要勾选web依赖即可。 2 添加 Maven 添加依赖 <dependency><groupId>com.dianping.cat</groupId><artifactId>cat-client</artifa…...

虚拟机/双系统Ubuntu扩容
虚拟机Ubuntu扩容 1.需要删除所有的快照 2.扩展虚拟机磁盘大小 虚拟机(M)→设置(s)→硬盘(SCSI)→扩展磁盘容量 3.Ubuntu内调整分区大小 安装gparted分区工具:sudo apt-get install gparted 启动gparted并resize分区 4.最后最好建一个快照,不然gg了…...
Nginx搭建本地服务器,无需购买服务器即可测试vue项目打包后的效果
一.前言 本文是在windows环境(Linux环境下其实也大同小异)下基于Nginx实现搭建本地服务器,手把手教你部署vue项目。 二.Nginx入门 1)下载安装 进入Nginx官网下载,选择stable版本下的windows版本下载即可 2)…...

SpringBoot 接口调用出现乱码解决 中文乱码
SpringBoot 接口调用出现乱码解决 package com.cxjg.mvc.util;import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration; import org.springframework.http.converter.HttpMessageConverter; import org.springfra…...

JDBC封装与设计模式
什么是 DAO ? Data Access Object(数据存取对象) 位于业务逻辑和持久化数据之间实现对持久化数据的访问 DAO起着转换器的作用,将数据在实体类和数据库记录之间进行转换。 ----------------------------------------------------- DAO模式的组成部分 …...

小程序扫描二维码获取网址,通过Jsoup进行解析
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 文章目录 前言 一、Jsoup是什么? 二、使用步骤 1.引入库 2.读入数据 总结 前言 vx开发小程序使用扫一扫时不同二维码展示的东西不一样,需要进行解析 提示&a…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...
