2023河南萌新联赛第(六)场:河南理工大学-C 旅游
2023河南萌新联赛第(六)场:河南理工大学
https://ac.nowcoder.com/acm/contest/63602/C
文章目录
- 2023河南萌新联赛第(六)场:河南理工大学
- 题意
- 解题思路
- 代码
题意
小C喜欢旅游,现在他要去DSH旅游,DSH里有 n n n个城市和 n − 1 n−1 n−1条双向道路(每条道路长度为1),每条道路连接两个城市,并且任意两个城市都可以通过这些的道路互相到达。现在小C要使用魔法指定传送到DSH里的一个城市,作为他旅游的出发城市,小C旅游遵从以下原则:
- 当小C抵达一个城市的时候,他会去跟当前这个城市相连的城市;
- 他只去他以前没有去过的城市;
- 在每个城市,小C以相同的概率移动去上述符合要求的城市;
当没有这样的城市(可走)时,小C就停下了。
由于小C太喜欢DSH了,所以请你告诉小C,在他可以指定传送出发城市的情况下,他的旅游路径的期望最大值是多少。
解题思路
先确定 1 1 1为根节点,设 d p x dp_x dpx表示以 x x x为根的子树内走过节点个数的期望值,则 d p x = 1 + 1 ∣ s o n x ∣ ∑ s ∈ s o n x d p s dp_x=1+\frac{1}{|son_x|}\sum_{s\in son_x}dp_s dpx=1+∣sonx∣1∑s∈sonxdps,求出后,设 f x f_x fx表示以 x x x为出发点,经过节点个数的期望值,显然 f 1 = d p 1 f_1=dp_1 f1=dp1,可以用换根 d p dp dp, O ( n ) O(n) O(n)求出 { f } \{f\} {f},对于 f x f_x fx,其值包括其原来的子树的贡献和原来的父亲 f a fa fa的贡献。首先考虑子树,贡献为 1 ∣ s o n x + 1 ∣ ∑ s ∈ s o n x f s \dfrac{1}{|son_x+1|}\sum_{s\in son_x}f_s ∣sonx+1∣1∑s∈sonxfs,可以发现 ∑ s ∈ s o n x f s = ( d p x − 1 ) × ∣ s o n x ∣ \sum_{s\in son_x}f_s=(dp_x-1)\times|son_x| ∑s∈sonxfs=(dpx−1)×∣sonx∣,所以为 ∣ s o n x ∣ ∣ s o n x + 1 ∣ ( d p x − 1 ) \dfrac{|son_x|}{|son_x+1|}(dp_x-1) ∣sonx+1∣∣sonx∣(dpx−1)。对于 f a fa fa的贡献,包括以 f a fa fa为根的树的期望减去以 x x x为儿子的贡献,为 v e c f a . s i z e ( ) × f f a − d p x − 1 v e c f a . s i z e ( ) − 1 × 1 ∣ s o n x ∣ + 1 \dfrac{vec_{fa}.size()\times f_{fa}-dp_x-1}{vec_{fa}.size()-1}\times\dfrac{1}{|son_x|+1} vecfa.size()−1vecfa.size()×ffa−dpx−1×∣sonx∣+11(之所以用 v e c f a . s i z e ( ) vec_{fa}.size() vecfa.size()是避免 f a = 1 fa=1 fa=1时再分类讨论),加上其本身,整理可得:
f x = 1 ∣ s o n x ∣ + 1 ( ( d p x − 1 ) × ∣ s o n x + 1 ∣ + v e c f a . s i z e ( ) × f f a − d a x − 1 v e c f a . s i z e ( ) − 1 ) + 1 f_x=\dfrac{1}{|son_x|+1}((dp_x-1)\times|son_x+1|+\dfrac{vec_{fa}.size()\times f_{fa}-da_x-1}{vec_{fa}.size()-1})+1 fx=∣sonx∣+11((dpx−1)×∣sonx+1∣+vecfa.size()−1vecfa.size()×ffa−dax−1)+1
记得 g g g表示的是节点数,答案要求路径长,要将最大值减一。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n;
double dp[N],f[N],ma;
vector<int>ve[N];
void dfs1(int u,int fa){int cnt=(ve[u].size()-(u!=1?1:0));for(auto v:ve[u]){if(v==fa)continue;dfs1(v,u);dp[u]+=1.0/cnt*dp[v];}dp[u]=dp[u]+1;
}
void dfs2(int u,int fa){ma=max(f[u],ma);int sum=ve[u].size();for(auto v:ve[u]){if(v==fa)continue;int cnt=ve[v].size()-1;f[v]=(1.0*(dp[v]-1)*cnt+(sum>1?(sum*f[u]-dp[v]-1)/(sum-1):1))/(cnt+1)+1;dfs2(v,u);}
}
int main(){cin>>n;for(int i=1;i<n;i++){int u,v;cin>>u>>v;ve[u].push_back(v);ve[v].push_back(u);}dfs1(1,0);f[1]=dp[1];dfs2(1,0);printf("%.3lf",ma-1);
}
相关文章:
场:河南理工大学-C 旅游)
2023河南萌新联赛第(六)场:河南理工大学-C 旅游
2023河南萌新联赛第(六)场:河南理工大学 https://ac.nowcoder.com/acm/contest/63602/C 文章目录 2023河南萌新联赛第(六)场:河南理工大学题意解题思路代码 题意 小C喜欢旅游,现在他要去DSH旅…...
)
C语言 常用工具型API ----------strchr()
函数原型 char *strchr(const char *str, int c) 参数 str-- 要被检索的 C 字符串。 c-- 在 str 中要搜索的字符。 功能 在参数str所指向的字符串中搜索第一次出现字符c(一个无符号字符)的位置 头文件 #include <string.h> 返回值 返回一…...

建造者模式的理论与实现
本文实践代码仓库:https://github.com/goSilver/my_practice 文章目录 一、定义二、作用三、实现四、总结 一、定义 建造者模式是一种创建复杂对象的设计模式。它将一个复杂对象的构建过程分解为多个简单的步骤,并且允许按照特定的顺序来构建对象。通过…...

非计算机科班如何顺利转码进入计算机领域?
文章目录 如何规划才能实现转码?计算机岗位发展前景?现阶段转码 总结 🎉欢迎来到Java学习路线专栏~探索非计算机科班如何顺利转码进入计算机领域 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页:IT陈寒的博客dz…...
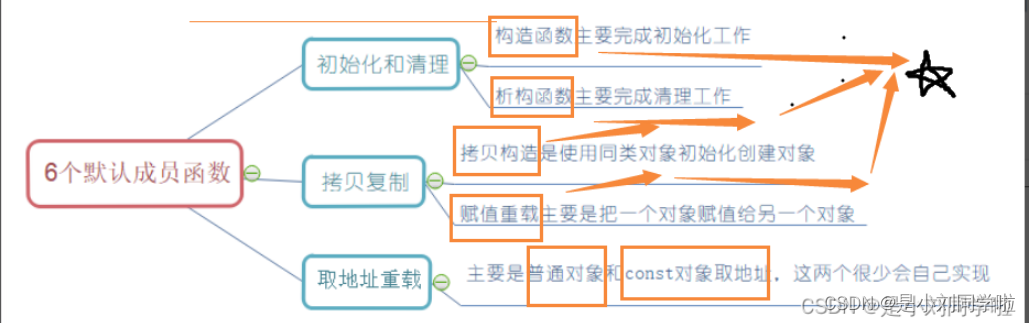
【C++类和对象】类有哪些默认成员函数呢?(下)
文章目录 一、类的6个默认成员函数二、日期类的实现2.1 运算符重载部分2.2 日期之间的运算2.3 整体代码1.Date.h部分2. Date.cpp部分 三. const成员函数四. 取地址及const取地址操作符重载扩展内容 总结 ヾ(๑╹◡╹)ノ" 人总要为过去的懒惰而付出代价ヾ(๑╹◡…...

springboot自定义banner的输出与源码解析
文章目录 一、介绍二、演示环境三、自定义banner1. 文本2. 图片3. placeholder占位符4. 关闭banner 四、源码分析1. 关闭banner2. banner模式3. banner打印器4. 打印banner① 获取banner② 打印banner 5. 版本号占位符的解析器6. 文本格式占位符的解析器7. 应用标题占位符的解析…...

LeetCode 141.环形链表
文章目录 💡题目分析💡解题思路🔔接口源码💡深度思考❓思考1❓思考2 题目链接👉 LeetCode 141.环形链表👈 💡题目分析 给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中…...
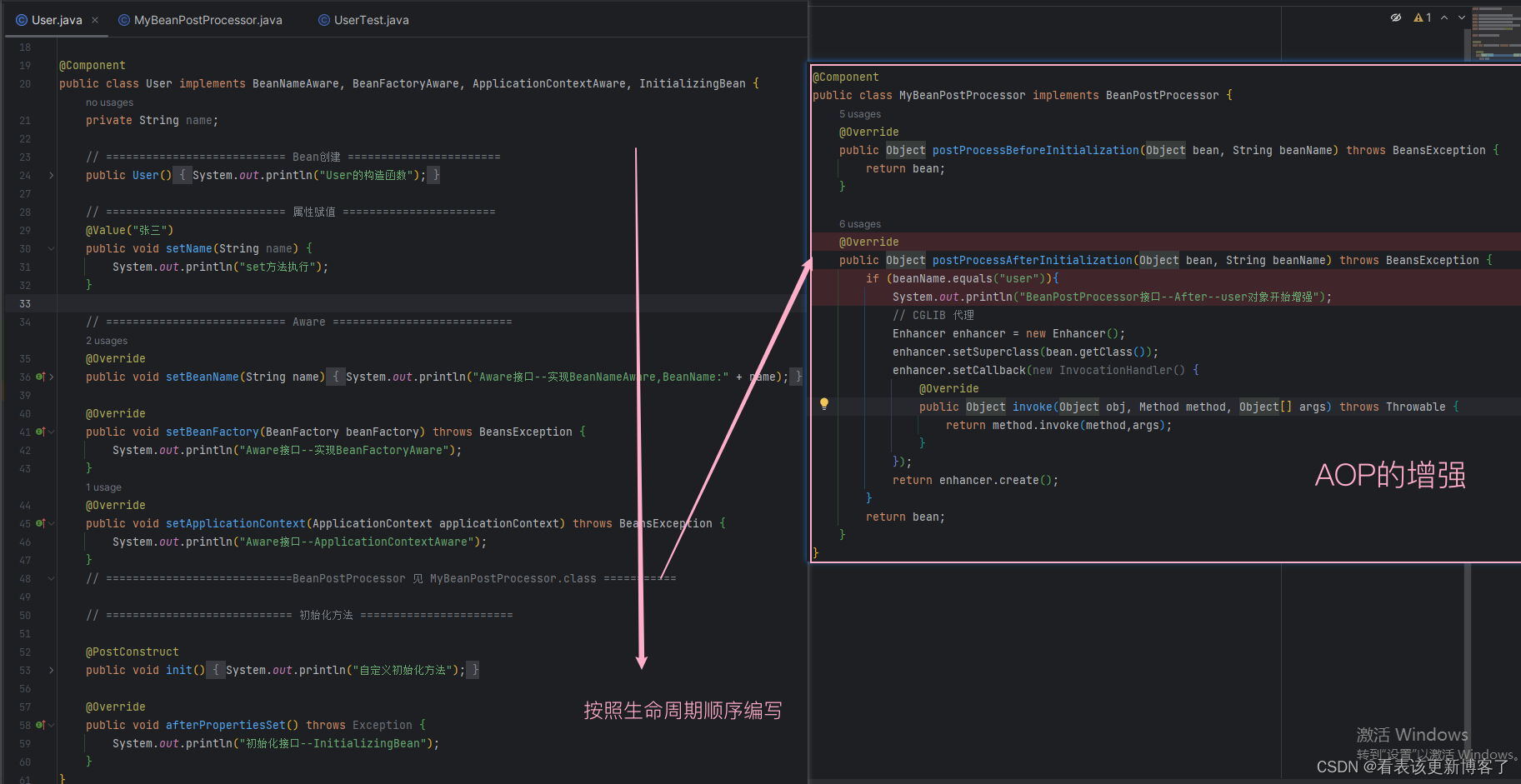
Spring-Bean的生命周期
目录 生命周期汇总 细分生命周期 1.实例化 2.属性赋值(依赖注入) 3.Aware接口 4.BeanPostProcessor接口 5.初始化 6.销毁 测试验证 类结构 业务类 测试类 生命周期汇总 Spring Bean 的生命周期见下图 (一定记忆好下图&#x…...
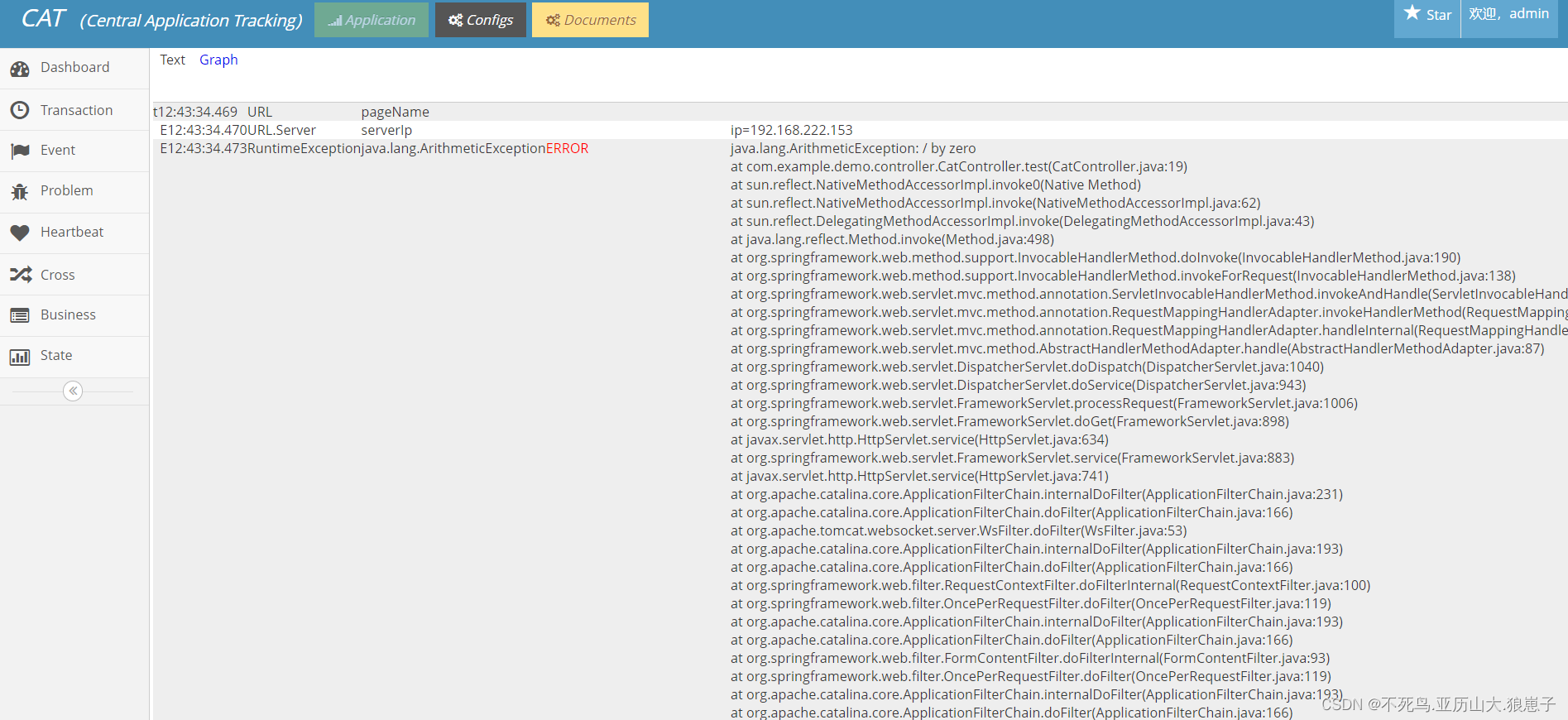
Cat(3):客户端集成—简单案例
接下来编写一个简单的springboot与Cat整合的案例 1 新建springboot项目 首先创建一个Spring Boot的初始化工程。只需要勾选web依赖即可。 2 添加 Maven 添加依赖 <dependency><groupId>com.dianping.cat</groupId><artifactId>cat-client</artifa…...

虚拟机/双系统Ubuntu扩容
虚拟机Ubuntu扩容 1.需要删除所有的快照 2.扩展虚拟机磁盘大小 虚拟机(M)→设置(s)→硬盘(SCSI)→扩展磁盘容量 3.Ubuntu内调整分区大小 安装gparted分区工具:sudo apt-get install gparted 启动gparted并resize分区 4.最后最好建一个快照,不然gg了…...
Nginx搭建本地服务器,无需购买服务器即可测试vue项目打包后的效果
一.前言 本文是在windows环境(Linux环境下其实也大同小异)下基于Nginx实现搭建本地服务器,手把手教你部署vue项目。 二.Nginx入门 1)下载安装 进入Nginx官网下载,选择stable版本下的windows版本下载即可 2)…...

SpringBoot 接口调用出现乱码解决 中文乱码
SpringBoot 接口调用出现乱码解决 package com.cxjg.mvc.util;import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration; import org.springframework.http.converter.HttpMessageConverter; import org.springfra…...

JDBC封装与设计模式
什么是 DAO ? Data Access Object(数据存取对象) 位于业务逻辑和持久化数据之间实现对持久化数据的访问 DAO起着转换器的作用,将数据在实体类和数据库记录之间进行转换。 ----------------------------------------------------- DAO模式的组成部分 …...

小程序扫描二维码获取网址,通过Jsoup进行解析
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 文章目录 前言 一、Jsoup是什么? 二、使用步骤 1.引入库 2.读入数据 总结 前言 vx开发小程序使用扫一扫时不同二维码展示的东西不一样,需要进行解析 提示&a…...
Kubernetes+EFK构建日志分析平台
目录 Elasticsearch产品介绍 Fluentd 工作原理 Kibana产品介绍 一、环境准备 前三个主机都要操作 1、主机初始化配置 2、部署docker环境 2、部署kubernetes集群 2.1、组件介绍 2.2、配置阿里云yum源 2.3、安装kubelet kubeadm kubectl 2.4、配置init-config.yaml …...
客服如何减轻工作压力?浅析客服压力管理方法
在现代商业领域中,客服是一项非常重要的工作,负责根据客户需求提供解决方案。客服工作不仅需要一定的专业知识和技能,还需要面对各种复杂、多变的情况,并拥有强大的应对压力的能力。客服从业人员的工作压力往往非常大,…...

知识储备--基础算法篇-二分搜索
1.前言 最近准备开始刷算法题了,搜了很多相关的帖子,下面三个很不错, 计算机视觉秋招准备过程看这个:计算机视觉算法工程师-秋招面经 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/399813916 复习深度学习相关…...

【MySQL系列】表内容的基本操作(增删查改)
「前言」文章内容大致是对MySQL表内容的基本操作,即增删查改。 「归属专栏」MySQL 「主页链接」个人主页 「笔者」枫叶先生(fy) 目录 一、MySQL表内容的增删查改1.1 Create1.1.1 单行数据全列插入1.1.2 多行数据指定列插入1.1.3 插入否则更新1.1.4 数据替换 1.2 Ret…...

docker搭建LNMP
docker安装 略 下载镜像 nginx:最新版php-fpm:根据自己需求而定mysql:根据自己需求定 以下是我搭建LNMP使用的镜像版本 rootVM-12-16-ubuntu:/docker/lnmp/php/etc# docker images REPOSITORY TAG IMAGE ID CREATED SIZE mysql 8.0…...

未出现过的最小正整数
给定一个长度为 n 的整数数组,请你找出未在数组中出现过的最小正整数。 样例 输入1:[-5, 3, 2, 3]输出1:1输入2:[1, 2, 3]输出2:4数据范围 1≤n≤105 , 数组中元素的取值范围 [−109,109]。 代码: c…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...
