Vue2集成Echarts实现可视化图表
一、依赖配置
1、引入echarts相关依赖
也可以卸载原有的,重新安装
卸载:npm uninstall echarts --save
安装:npm install echarts@4.8.0 --save
引入水球图形依赖
npm install echarts-liquidfill@2.0.2 --save
水球图可参考文档:
https://gitcode.net/mirrors/ecomfe/echarts-liquidfill?utm_source=csdn_github_accelerator
引入3D效果图依赖:
npm install echarts-gl@2.0.9 --save
安装完成后,在package.json文件中查看,如图:
2、修改配置文件
在main.js文件中,配置如下信息:
// ECharts 图表展示
import * as echarts from 'echarts';
// 球形图
import 'echarts-liquidfill';
Vue.prototype.$echarts = echarts;
配置完成后,如图:

3、主题风格下载
3.1 在官网下载主题风格
打开官网 Apache ECharts
点击下载-主题下载:
然后就可以下载对应的主题配置文件。
也可以点击【定制主题】选择合适的风格下载主题风格,如图:
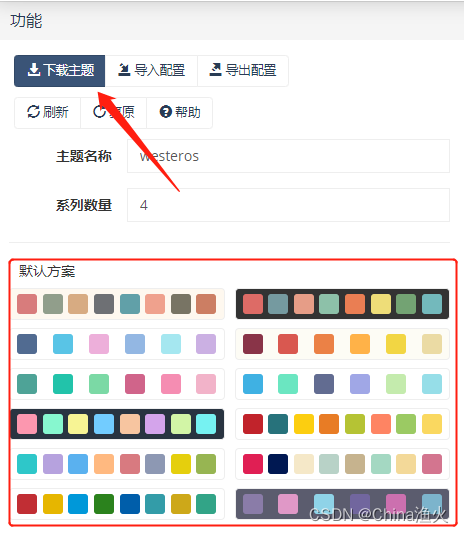
选择完成后,点下载主题,分为JS版本和JSON版本两种方式,可根据需要下载
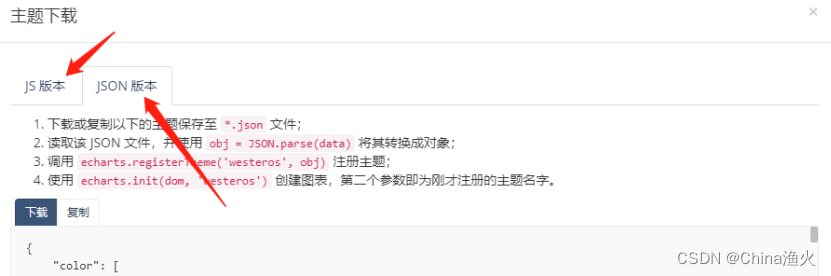
下载完成后,把JSON文件放到项目中,如图:
我这里下载了两个风格,可自由选择。
4、代码实现
引用下载好的依赖:

以饼图为例,大致代码结构,可参照官网全部实例,地址如下:
Examples - Apache ECharts 样例如图:
点击一个图形进去,可看到源码和文档配置说明,如图:

配置项说明,如图:
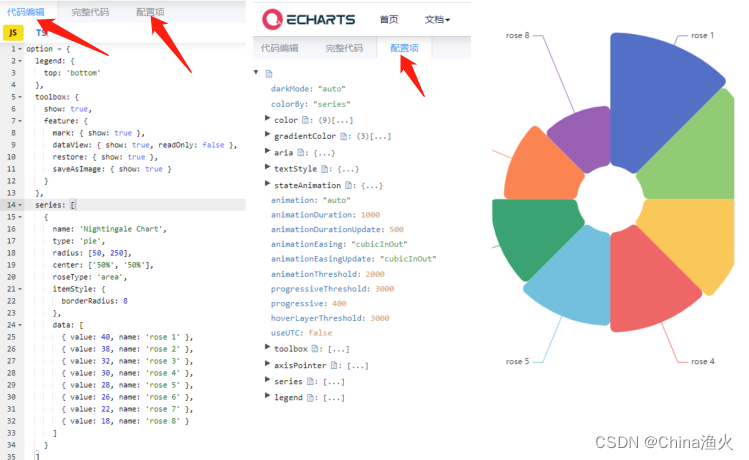
然后,获取到图形的主题结构后,引入到代码中:
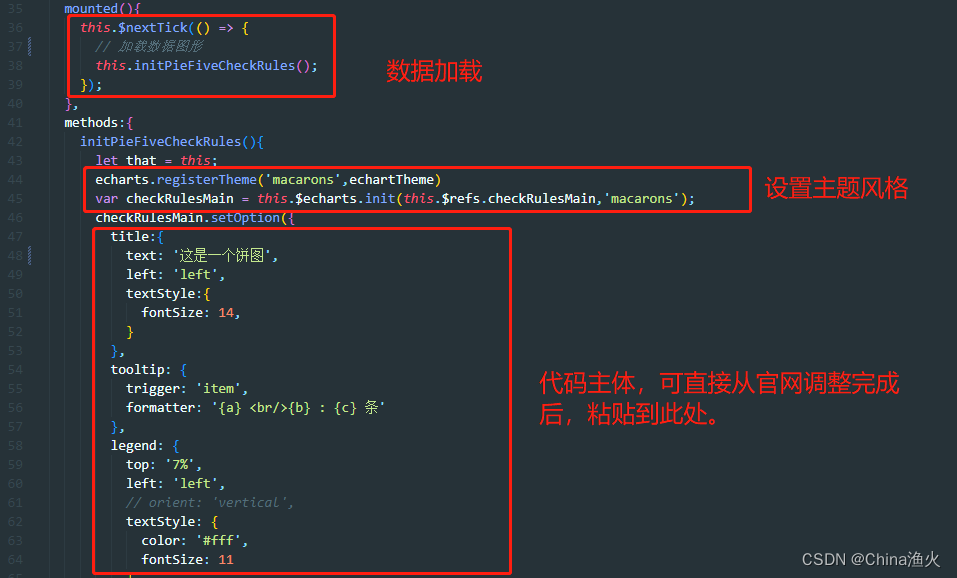
5、小结
Vue2集成Echarts实现可视化图表大致流程就是如上文所述,具体开发中,可根据自身需求和官网实例,以及官网示例参数说明进行调整。
相关文章:

Vue2集成Echarts实现可视化图表
一、依赖配置 1、引入echarts相关依赖 也可以卸载原有的,重新安装 卸载:npm uninstall echarts --save 安装:npm install echarts4.8.0 --save 引入水球图形依赖 npm install echarts-liquidfill2.0.2 --save 水球图可参考文档࿱…...
3 Python的数据类型
概述 在上一节,我们介绍了Python的基础语法,包括:编码格式、标识符、关键字、注释、多行、空行、缩进、引号、输入输出、import、运算符、条件控制、循环等内容。Python是一种动态类型的编程语言,这意味着当你创建一个变量时&…...
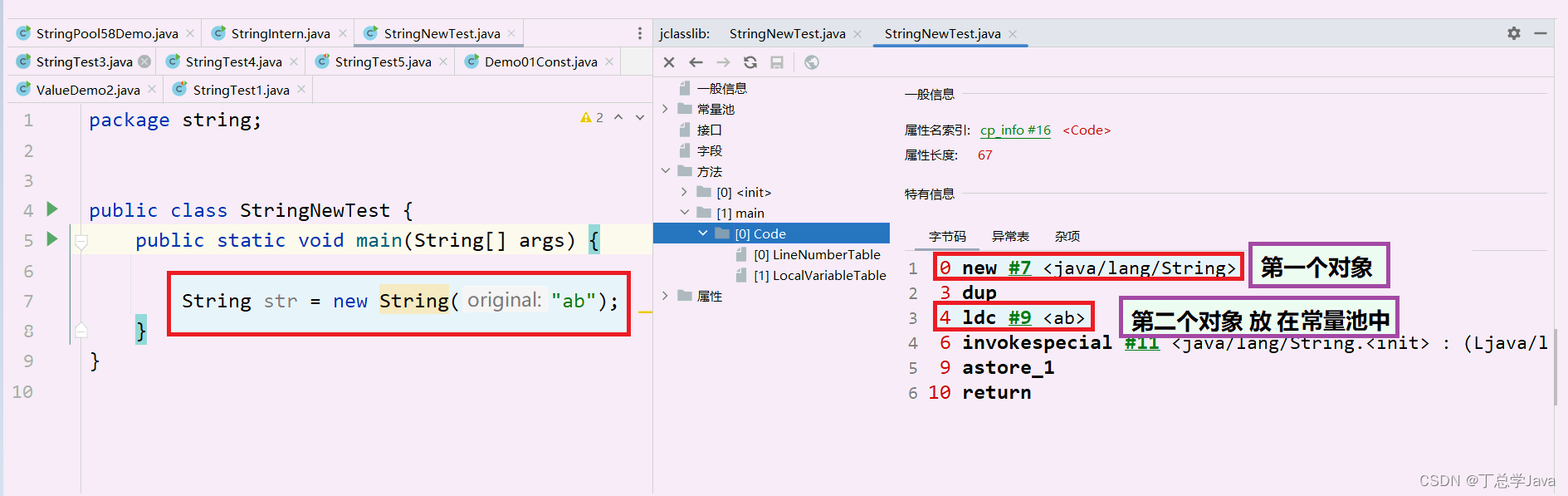
new String()到底创建了几个对象
题目: new String("abc")会创建几个对象? 看字节码,就知道是两个。...

第五十五天
CSS3 ●背景 CSS3 中包含几个新的背景属性,提供更大背景元素控制: •background-image:添加背景图片。不同的背景图像和图像用逗号隔开,所有的图片中显示在最顶端的为第一张。 •background-size:指定背景图像的大…...

【推荐】深入浅出benan的生命周期
目录 1.spring 管理JavaBean的过程(生命周期) 2.spring的JavaBean管理中单例模式及原型(多例)模式 2.1 . 默认为单例,但是可以配置多例 2.2.举例论证 2.2.1 默认单例 2.2.2 设置多例 2.2.3单例与多例的初始化的时…...
mysql使用redis+canal实现缓存一致性
目录 一、开启binlog日志 1.首先查看是否开启了binlog 2、开启binlog日志,并重启mysql服务 二、授权 canal 链接 MySQL 账号具有作为 MySQL slave 的权限 三、下载配置canal 1、下载 canal, 访问 release 页面 , 选择需要的包下载, 如以 1.0.17 版本为例 2、 …...
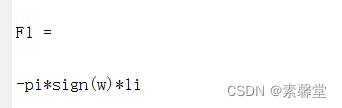
9.利用matlab完成 泰勒级数展开 和 符号表达式傅里叶变换和反变换 (matlab程序)
1.简述 matlab之傅里叶变换和逆变换 首先生成一个方波(或者其他组合波形),然后对这个信号做傅里叶变换,拆解到频域,可以看到这个信号是由哪些频率的信号叠加而来。 然后把频域信号,用傅里叶逆变换恢复到时…...

文字点选验证码识别(上)-YOLO位置识别
声明 本文以教学为基准、本文提供的可操作性不得用于任何商业用途和违法违规场景。 本人对任何原因在使用本人中提供的代码和策略时可能对用户自己或他人造成的任何形式的损失和伤害不承担责任。 如有侵权,请联系我进行删除。 文章中没有代码,只有过程思路,请大家谨慎订阅。…...

ssh远程连接慢解决方法
一、关闭SERVER上的GSS认证 将GSSAPIAuthentication改为no ,如果在配置文件中,以下值是被注释的就拿掉注释,因为默认开关就是yes # vi /etc/ssh/sshd_config GSSAPIAuthentication no二、关闭SERVER上DNS反向解析 在linux中,默认就是开启了S…...
10.4K Star!程序员为程序员针对性优化的开源免费笔记
平时我一直用Notion来记录内容为主,但也一直关注着其他开源产品。上周正好看到一款非常受欢迎的开源免费笔记,今天就推荐给大家:VNote。 VNote一个由程序员为程序员打造的开源笔记应用,基于Qt开发,专注于使用 Markdown…...
ppt中线材相交接的地方,如何绘画
ppt中线材相交接的地方: 在ppt中绘画线材相互交接的地方: 1.1绘图工具中的“弧形” 1.2小技巧 “弧形”工具点一下,在ppt中如下 1.3拖动活动点进行调整图形 1.4绘画圆弧 1.5调整“圆弧”的大小,鼠标放在“黄色点”位置…...
[VS/C++]如何更好的配置DLL项目中的成品输出
注意,解决方案与项目不放在同一个文件夹中,即不选中图中选项 直入主题 首先右键项目选择属性,或者选中项目然后AltEnter 选择配置属性下的常规 分别在四种配置中编辑输出目录如下 注意,四种配置要分别配置,一个个来…...

REC 系列 Visual Grounding with Transformers 论文阅读笔记
REC 系列 Visual Grounding with Transformers 论文阅读笔记 一、Abstract二、引言三、相关工作3.1 视觉定位3.2 视觉 Transformer 四、方法4.1 基础的视觉和文本编码器4.2 定位编码器自注意力的文本分支文本引导自注意力的视觉分支 4.3 定位解码器定位 query 自注意力编码器-解…...

Linux常用命令总结
Linux是一种自由和开放源代码的操作系统,它被广泛用于服务器和其他大型系统中。然而,如果你刚开始使用Linux,可能会对如何有效地操作感到困惑。这篇文章将介绍一些常用的Linux命令,帮助你更好地理解和使用这个强大的系统。 文件和…...
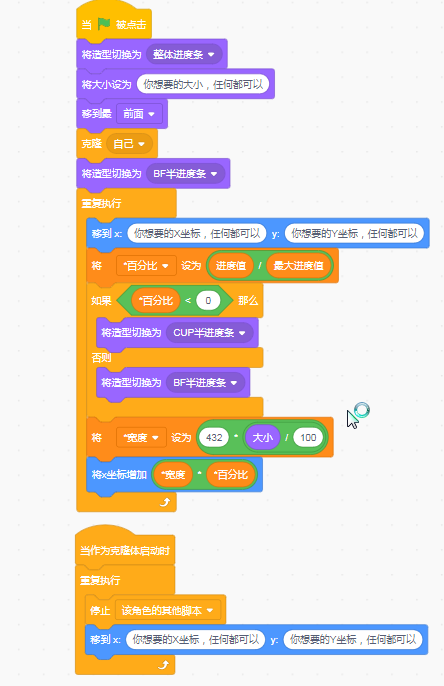
Scratch 之 制作超丝滑 FNF 推条
这个教程是不用画笔的,所以不用担心推条是最后一层了! 导入素材 你以为真是这样吗?NO,NO,NO,其实是这样的 没错,中间是空的!中间是空的!中间是空的!…...

java通过反射,动态调用指定注解的方法
SpringBootTest RunWith(SpringRunner.class) public class AnnoTest {Autowiredprivate ApplicationContext applicationContext;Testpublic void test(){// 获取有指定注解的BeanMap<String, Object> annotationMap applicationContext.getBeansWithAnnotation(CacheC…...

QT学习方法
1 .类的学习方法 第一步:从UI文件中,找到界面的类—QMainWindow第二步:在Qt Creator工具中,找到“帮助”按钮,进入到帮助菜单界面,在选择"索引",在Look for:输入类名,找到类名,双击条目中的类名,在右侧会显示出来类的详细内容第三步:在右侧,可根据内容目录…...

C++中的类型擦除技术
文章目录 一、C类型擦除Type Erasure技术1.虚函数2.模板和函数对象 二、任务队列1.基于特定类型的方式实现2.基于任意类型的方式实现 参考: 一、C类型擦除Type Erasure技术 C中的类型擦除(Type Erasure)是一种技术,用于隐藏具体类…...

激光雷达 01 线数
一、线数 对于 360 旋转式和一维转镜式架构的激光雷达来说,有几组激光收发模块,垂直方向上就有几条线,被称为线数。这种情况下,线数就等同于激光雷达内部激光器的数量[参考]。 通俗来讲,线数越高,激光器的…...
PHP 公交公司充电桩管理系统mysql数据库web结构apache计算机软件工程网页wamp
一、源码特点 PHP 公交公司充电桩管理系统是一套完善的web设计系统,对理解php编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。 源码下载 https://download.csdn.net/download/qq_41221322/88220946 论文下…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
