哈夫曼树(赫夫曼树、最优树)详解
目录
哈夫曼树(赫夫曼树、最优树)详解
哈夫曼树相关的几个名词
什么是哈夫曼树
构建哈夫曼树的过程
哈弗曼树中结点结构
构建哈弗曼树的算法实现
哈夫曼树(赫夫曼树、最优树)详解
哈夫曼树相关的几个名词
路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径。图 1 中,从根结点到结点 a 之间的通路就是一条路径。
路径长度:在一条路径中,每经过一个结点,路径长度都要加 1 。例如在一棵树中,规定根结点所在层数为1层,那么从根结点到第 i 层结点的路径长度为 i - 1 。图 1 中从根结点到结点 c 的路径长度为 3。
结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权。例如,图 1 中结点 a 的权为 7,结点 b 的权为 5。
结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。例如,图 1 中结点 b 的带权路径长度为 2 * 5 = 10 。
树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL” 。例如图 1 中所示的这颗树的带权路径长度为:
WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3
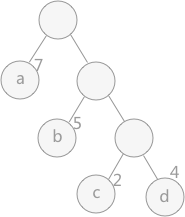
图1 哈夫曼树
什么是哈夫曼树
当用 n 个结点(都做叶子结点且都有各自的权值)试图构建一棵树时,如果构建的这棵树的带权路径长度最小,称这棵树为“最优二叉树”,有时也叫“赫夫曼树”或者“哈夫曼树”。
在构建哈弗曼树时,要使树的带权路径长度最小,只需要遵循一个原则,那就是:权重越大的结点离树根越近。在图 1 中,因为结点 a 的权值最大,所以理应直接作为根结点的孩子结点。
构建哈夫曼树的过程
对于给定的有各自权值的 n 个结点,构建哈夫曼树有一个行之有效的办法:
- 在 n 个权值中选出两个最小的权值,对应的两个结点组成一个新的二叉树,且新二叉树的根结点的权值为左右孩子权值的和;
- 在原有的 n 个权值中删除那两个最小的权值,同时将新的权值加入到 n–2 个权值的行列中,以此类推;
- 重复 1 和 2 ,直到所以的结点构建成了一棵二叉树为止,这棵树就是哈夫曼树。
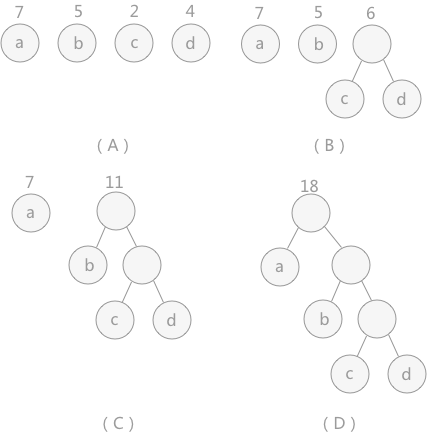
图 2 哈夫曼树的构建过程
图 2 中,(A)给定了四个结点a,b,c,d,权值分别为7,5,2,4;第一步如(B)所示,找出现有权值中最小的两个,2 和 4 ,相应的结点 c 和 d 构建一个新的二叉树,树根的权值为 2 + 4 = 6,同时将原有权值中的 2 和 4 删掉,将新的权值 6 加入;进入(C),重复之前的步骤。直到(D)中,所有的结点构建成了一个全新的二叉树,这就是哈夫曼树。
哈弗曼树中结点结构
构建哈夫曼树时,首先需要确定树中结点的构成。由于哈夫曼树的构建是从叶子结点开始,不断地构建新的父结点,直至树根,所以结点中应包含指向父结点的指针。但是在使用哈夫曼树时是从树根开始,根据需求遍历树中的结点,因此每个结点需要有指向其左孩子和右孩子的指针。
所以,哈夫曼树中结点构成用代码表示为:
- //哈夫曼树结点结构
- typedef struct {
- int weight;//结点权重
- int parent, left, right;//父结点、左孩子、右孩子在数组中的位置下标
- }HTNode, *HuffmanTree;
构建哈弗曼树的算法实现
构建哈夫曼树时,需要每次根据各个结点的权重值,筛选出其中值最小的两个结点,然后构建二叉树。
查找权重值最小的两个结点的思想是:从树组起始位置开始,首先找到两个无父结点的结点(说明还未使用其构建成树),然后和后续无父结点的结点依次做比较,有两种情况需要考虑:
- 如果比两个结点中较小的那个还小,就保留这个结点,删除原来较大的结点;
- 如果介于两个结点权重值之间,替换原来较大的结点;
实现代码:
- //HT数组中存放的哈夫曼树,end表示HT数组中存放结点的最终位置,s1和s2传递的是HT数组中权重值最小的两个结点在数组中的位置
- void Select(HuffmanTree HT, int end, int *s1, int *s2)
- {
- int min1, min2;
- //遍历数组初始下标为 1
- int i = 1;
- //找到还没构建树的结点
- while(HT[i].parent != 0 && i <= end){
- i++;
- }
- min1 = HT[i].weight;
- *s1 = i;
- i++;
- while(HT[i].parent != 0 && i <= end){
- i++;
- }
- //对找到的两个结点比较大小,min2为大的,min1为小的
- if(HT[i].weight < min1){
- min2 = min1;
- *s2 = *s1;
- min1 = HT[i].weight;
- *s1 = i;
- }else{
- min2 = HT[i].weight;
- *s2 = i;
- }
- //两个结点和后续的所有未构建成树的结点做比较
- for(int j=i+1; j <= end; j++)
- {
- //如果有父结点,直接跳过,进行下一个
- if(HT[j].parent != 0){
- continue;
- }
- //如果比最小的还小,将min2=min1,min1赋值新的结点的下标
- if(HT[j].weight < min1){
- min2 = min1;
- min1 = HT[j].weight;
- *s2 = *s1;
- *s1 = j;
- }
- //如果介于两者之间,min2赋值为新的结点的位置下标
- else if(HT[j].weight >= min1 && HT[j].weight < min2){
- min2 = HT[j].weight;
- *s2 = j;
- }
- }
- }
注意:s1和s2传入的是实参的地址,所以函数运行完成后,实参中存放的自然就是哈夫曼树中权重值最小的两个结点在数组中的位置。
构建哈弗曼树的代码实现如下:
- //HT为地址传递的存储哈夫曼树的数组,w为存储结点权重值的数组,n为结点个数
- void CreateHuffmanTree(HuffmanTree *HT, int *w, int n)
- {
- if(n<=1) return; // 如果只有一个编码就相当于0
- int m = 2*n-1; // 哈夫曼树总节点数,n就是叶子结点
- *HT = (HuffmanTree) malloc((m+1) * sizeof(HTNode)); // 0号位置不用
- HuffmanTree p = *HT;
- // 初始化哈夫曼树中的所有结点
- for(int i = 1; i <= n; i++)
- {
- (p+i)->weight = *(w+i-1);
- (p+i)->parent = 0;
- (p+i)->left = 0;
- (p+i)->right = 0;
- }
- //从树组的下标 n+1 开始初始化哈夫曼树中除叶子结点外的结点
- for(int i = n+1; i <= m; i++)
- {
- (p+i)->weight = 0;
- (p+i)->parent = 0;
- (p+i)->left = 0;
- (p+i)->right = 0;
- }
- //构建哈夫曼树
- for(int i = n+1; i <= m; i++)
- {
- int s1, s2;
- Select(*HT, i-1, &s1, &s2);
- (*HT)[s1].parent = (*HT)[s2].parent = i;
- (*HT)[i].left = s1;
- (*HT)[i].right = s2;
- (*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;
- }
- }
注意,如果使用此程序,对权重值分别为 2、8、7、6、5 的节点构建哈夫曼树,最终效果如图 4(A) 所示。但其实,图 4(B) 中显示的哈夫曼树也满足条件,这两棵树的带权路径长度相同。

图 4 两种哈夫曼树
之所以使用此程序构建的哈夫曼树,是图 4(A) 而不是 4(B),是因为在构建哈夫曼树时,结点 2 和结点 5 构建的新的结点 7 存储在动态树组中位置,比权重值为 7 节点的存储位置还靠后,所以,在程序继续选择两个权值最小的结点时,直接选择了的叶子结点 6 和 7 。
相关文章:

哈夫曼树(赫夫曼树、最优树)详解
目录 哈夫曼树(赫夫曼树、最优树)详解 哈夫曼树相关的几个名词 什么是哈夫曼树 构建哈夫曼树的过程 哈弗曼树中结点结构 构建哈弗曼树的算法实现 哈夫曼树(赫夫曼树、最优树)详解 哈夫曼树相关的几个名词 路径:…...
智慧建筑工地平台,通过信息化技术、物联网、人工智能技术,实现对施工全过程的实时监控、数据分析、智能管理和优化调控
智慧工地是指通过信息化技术、物联网、人工智能技术等手段,对建筑工地进行数字化、智能化、网络化升级,实现对施工全过程的实时监控、数据分析、智能管理和优化调控。智慧工地的建设可以提高工地的安全性、效率性和质量,降低施工成本…...
Springboot 实践(8)springboot集成Oauth2.0授权包,对接spring security接口
此文之前,项目已经添加了数据库DAO服务接口、资源访问目录、以及数据访问的html页面,同时项目集成了spring security,并替换了登录授权页面;但是,系统用户存储代码之中,而且只注册了admin和user两个用户。在…...
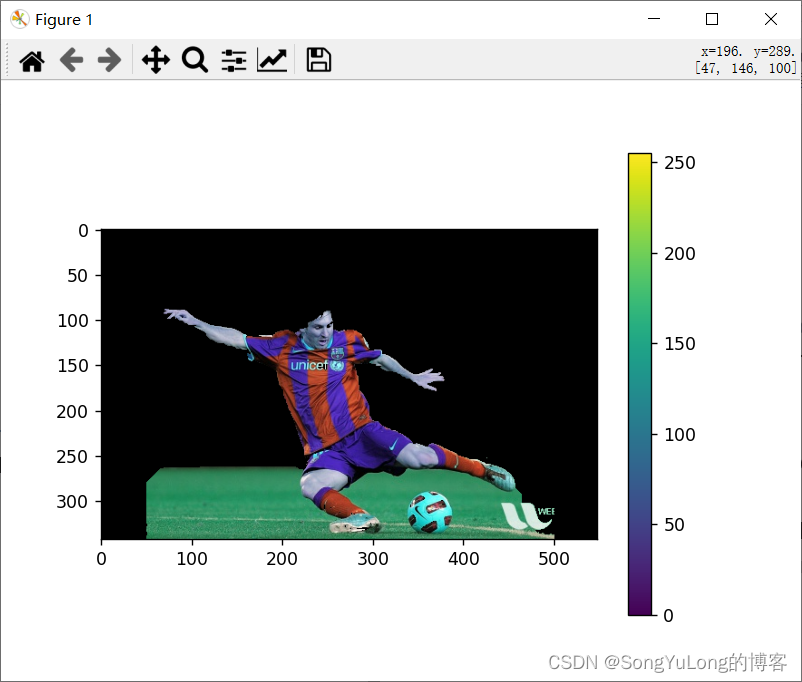
OpenCV-Python中的图像处理-GrabCut算法交互式前景提取
OpenCV-Python中的图像处理-GrabCut算法交互式前景提取 Python-OpenCV中的图像处理-GrabCut算法交互式前景提取 Python-OpenCV中的图像处理-GrabCut算法交互式前景提取 cv2.grabCut(img: Mat, mask: typing.Optional[Mat], rect, bgdModel, fgdModel, iterCount, mode…) img…...

leetcode原题 后继者:找出二叉搜索树中指定节点的“下一个”节点
题目: 设计一个算法,找出二叉搜索树中指定节点的“下一个”节点(也即中序后继)。 如果指定节点没有对应的“下一个”节点,则返回null。 示例: 输入: root [2,1,3], p 1 2 / \ 1 3 输出: 2 解题思路…...

pyqt5 QlineEdit 如何设置只能输入数字
在 PyQt(Python中的一个GUI库)中,可以使用QLineEdit小部件的setValidator()方法来限制用户输入的内容。要让QLineEdit只能输入数字,你可以使用QIntValidator或QDoubleValidator。下面是一个示例代码,展示如何设置只能输…...

ubuntu中安装python
最简单方便的是 apt 使用第三方的 ppa 源,然后直接 apt 安装 python3.9 安装 software-properties-common 获取add-apt-repository命令:apt install -y software-properties-common添加第三方的 ppa 源:add-apt-repository ppa:deadsnakes/p…...
LeetCode150道面试经典题-- 快乐数(简单)
1.题目 编写一个算法来判断一个数 n 是不是快乐数。 「快乐数」 定义为: 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。如果这个过程 结果为 1&am…...

科研论文配图----第一章笔记
第一章笔记 科研论文的绘制基础 科研论文配图的分类与构成 根据呈现方式,科研论文配图可分为线性图、灰度图、照片彩图和综合配图 4 种类型。 其中,线性图是主要和常用的配图类型,也是本书重点介绍的配图类型。 科研论文配图的格式和尺寸 格…...

OpenHarmony Meetup 广州站 OpenHarmony正当时—技术开源
招募令 OpenHarmony Meetup 广州站 火热招募中,等待激情四射的开发者,线下参与OpenHarmonyMeetup线下交流 展示前沿技术、探讨未来可能、让你了解更多专属OpenHarmony的魅力 线下参与,先到先得,仅限20个名额! 报名截止时间8月23日…...

如何使用PHP Smarty模板实现静态页面生成
首先,你需要从Smarty官网下载这个神奇的文件。然后,你需要在你的PHP文件中引入Smarty类。就像这样: require_once(Smarty.class.php);现在,我们要创建一个Smarty实例。这就像打开一个新的文件,只不过这个文件是可以和…...
【 Cocos Creator 项目实战】益智游戏《2048》(附带完整源码工程)
本文乃Siliphen原创,转载请注明出处 目录 游戏介绍 概述 游戏整体流程 游戏框架设计 主要流程控制类 本文项目的代码组织结构 构建游戏世界 数字方块 地图 触摸手势识别 防触摸抖动 判断用户输入的方向 地图 任意大小的地图 初始化地图大小 地图绘制…...

剑指Offer68-II.二叉树的最近公共祖先 C++
1、题目描述 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以…...

【JAVA】我们该如何规避代码中可能出现的错误?(一)
个人主页:【😊个人主页】 系列专栏:【❤️初识JAVA】 文章目录 前言三种类型的异常异常处理JAVA内置异常类Exception 类的层次 前言 异常是程序中的一些错误,但并不是所有的错误都是异常,并且错误有时候是可以避免的&…...
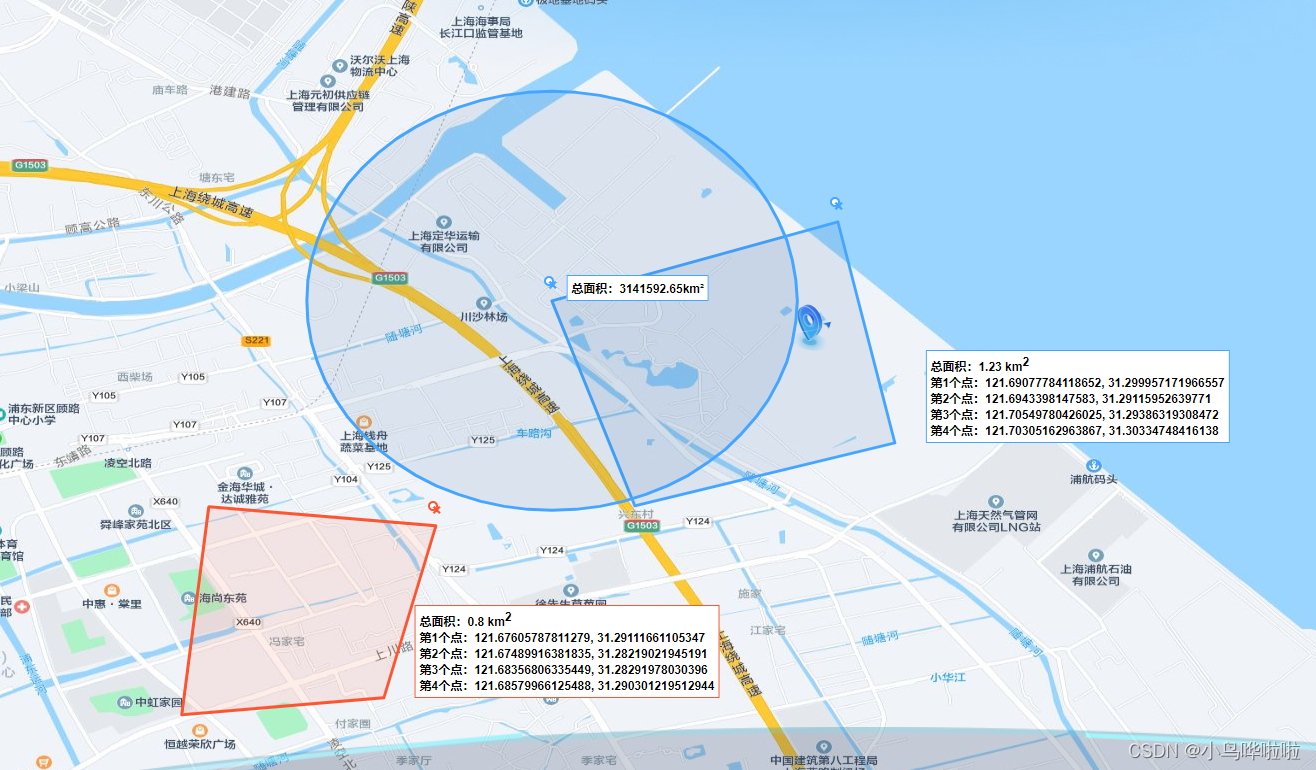
openLayers实战(八):坐标系及其转换
坐标系介绍 EPSG: 3857 --web地图,基于球体的、web墨卡托投影(伪墨卡托投影Pseudo-Mercator)的投影坐标系,范围为纬度85度以下,由于google地图最先使用而成为事实标准。至今,大多互联网地图都使用EPSG3857&…...
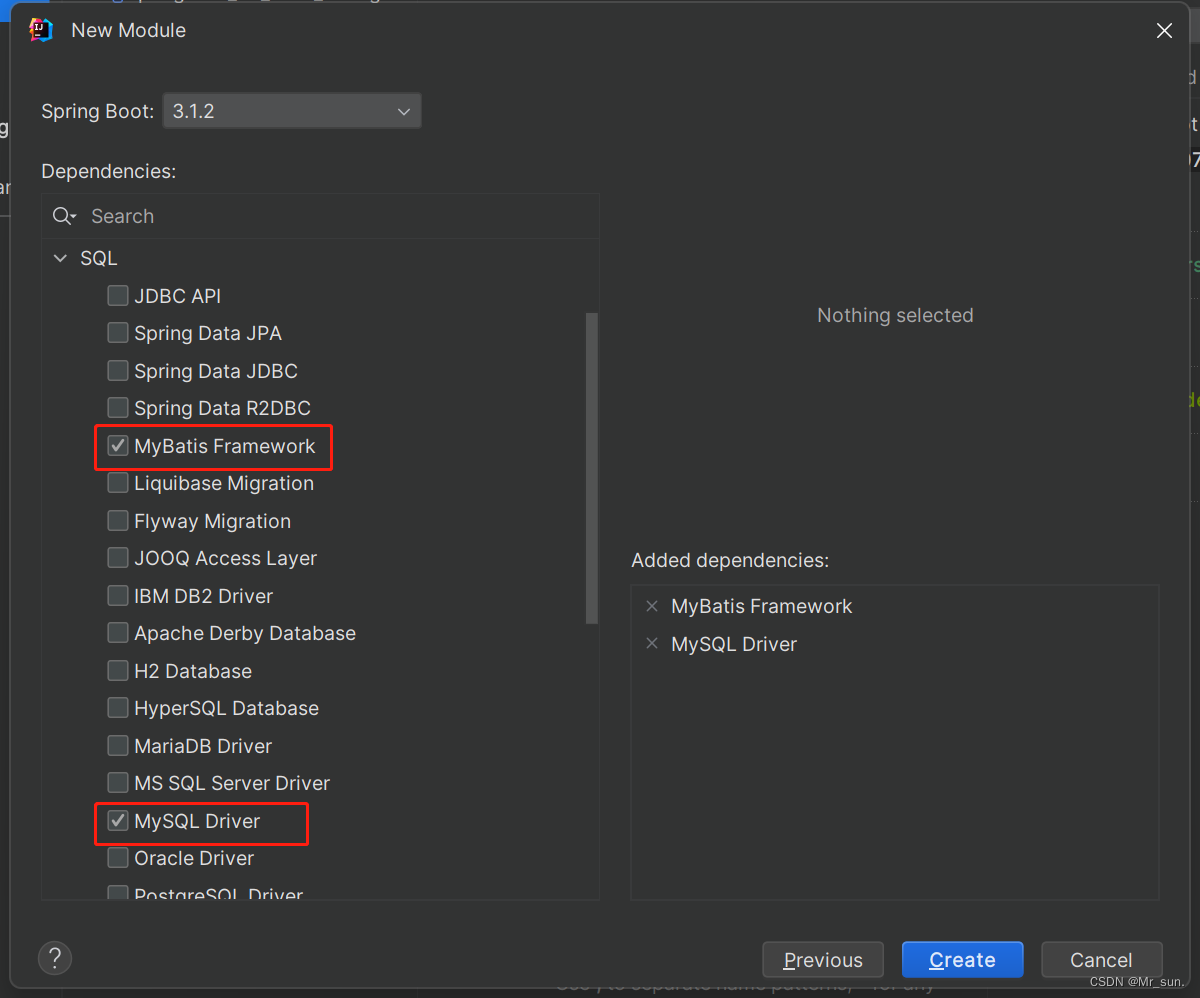
DAY06_SpringBoot—简介基础配置yaml多环境开发配置整合第三方技术
目录 一 SpringBoot简介1. 入门案例问题导入1.1 入门案例开发步骤1.2 基于SpringBoot官网创建项目1.3 SpringBoot项目快速启动 2. SpringBoot概述问题导入2.1 起步依赖2.2 辅助功能 二 基础配置1. 配置文件格式问题导入1.1 修改服务器端口1.2 自动提示功能消失解决方案1.3 Spri…...

无涯教程-Perl - setpwent函数
描述 此功能将枚举设置(或重置)到密码条目集的开头。应该在第一次调用getpwent之前调用此函数。 语法 以下是此函数的简单语法- setpwent返回值 此函数不返回任何值。 例 以下是显示其基本用法的示例代码- #!/usr/bin/perlwhile(($name, $passwd, $uid, $gid, $quota, …...
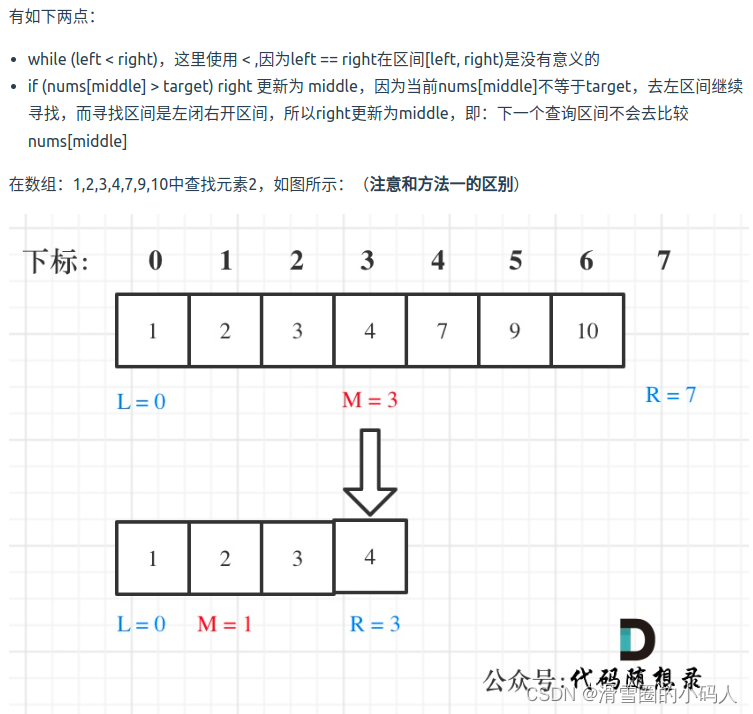
代码随想录-数组篇
2-二分查找 方法一: 左闭右闭,[left, right] class Solution { public:int search(vector<int>& nums, int target) {//[left, right]int left 0;int right nums.size() - 1 ;while(left < right){int middle left ((right - left)…...
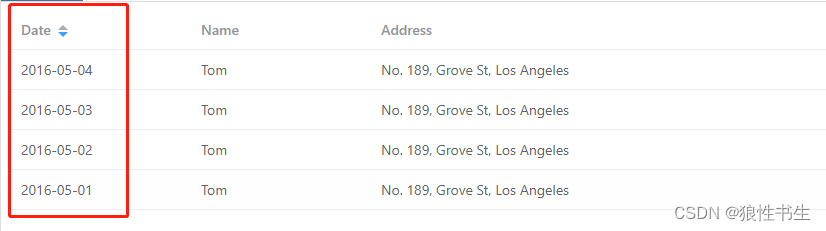
vue3+element-plus表格默认排序default-sort失效问题
场景 在使用动态数据渲染的场景,el-table设置默认属性default-sort失效。 原因 el-table的default-sort属性是针对静态数据的,如果是动态数据,default-sort则无法监听到。 案例:静态数据 <template><el-table:data&…...
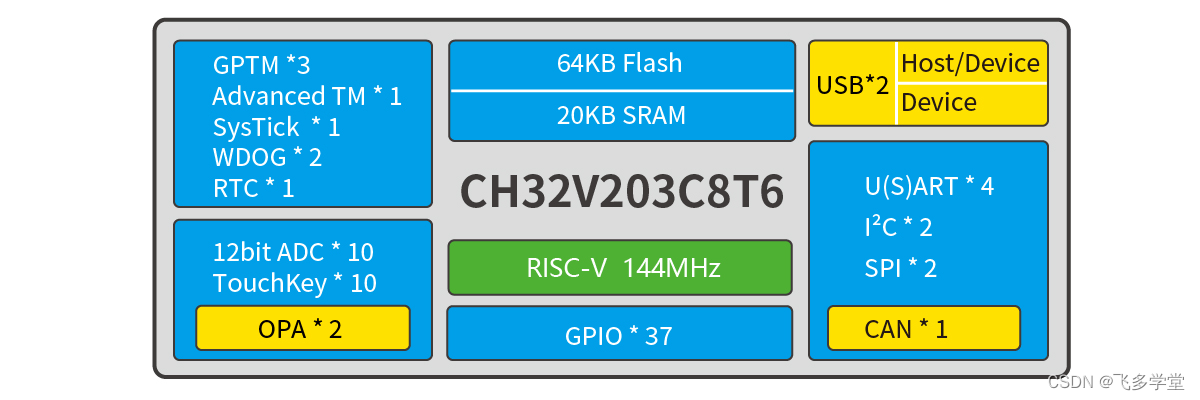
CH32V203 单片机 I2C 使用
CH32V203系列是基于32位RISC-V内核设计的工业级增强型低功耗通用微控制器,高性能,最高支持144MHz系统主频,低功耗,运行功耗低至45uA/MHz。CH32V203集成双路USB接口,支持USB Host主机及USB Device设备功能,具…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
