当前位置： 首页 > news >正文

2.js中attr()用来修改或者添加属性或者属性值

news 2026/2/8 19:20:29

attr()可以用来修改或者添加属性或者属性值
例：<input type="button" class="btn btn-info" id="subbtn" style="font-size:12px" value="我也说一句"/>
1.如果想获取input中value的值

$('#subbtn').attr('value'); 


2.如果想改变value的值
将‘我也说一句’改为'收起'；
$('#subbtn').attr('value','收起');   
也可以用来修改其他属性，value是属性，后面是属性的值


3.可以传入function(){} 
$('#subbtn').attr(attribute, function(index, oldValue){});
attribute：规定属性的名称。
函数返回属性的新值。
该函数可接收并使用选择器的 index 值和当前属性值
 

相关文章：

2.js中attr()用来修改或者添加属性或者属性值

attr()可以用来修改或者添加属性或者属性值 例&#xff1a;<input type"button" class"btn btn-info" id"subbtn" style"font-size:12px" value"我也说一句"/>1.如果想获取input中value的值 $(#subbtn).attr(value);…...

编程日记 2023/8/19 5:50:43

【虫洞攻击检测】使用多层神经网络的移动自组织网络中的虫洞攻击检测研究（Matlab代码实现）

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 ⛳️座右铭&a…...

编程日记 2023/8/19 5:49:41

微分流形学习之一：基本定义

微分流形学习之一&#xff1a;基本定义引入 引言一、微分流形的历史简介二、拓扑空间三、微分流形 引言 本文是作者在学习微分流形的时候的笔记&#xff0c;尽量严格完整&#xff0c;并带有一定理解&#xff0c;绝不是结论的简单罗列。如果读者知道数学分析中的 ϵ − δ \ep…...

编程日记 2023/8/19 5:48:40

[C++]笔记-制作自己的静态库

一.静态库的创建 在项目属性c/c里面,选用无预编译头,创建头文件与cpp文件,需要注意release模式下还是debug模式,在用库时候要与该模式相匹配,库的函数实现是外界无法看到的,最后在要使用的项目里面导入.h文件和.lib文件 二.使用一个循环给二维数组赋值 行数 : 第几个元素 / …...

编程日记 2023/8/19 5:47:39

优酷视频码率、爱奇艺视频码率、B站视频码率、抖音视频码率对比

优酷视频码率、爱奇艺视频码率与YouTube视频码率对比 优酷视频码率&#xff1a; 优酷的视频码率可以根据视频质量、分辨率和内容类型而变化。一般而言&#xff0c;优酷提供了不同的码率选项&#xff0c;包括较低的标清&#xff08;SD&#xff09;码率和较高的高清&#xff08;…...

编程日记 2023/8/19 5:46:38

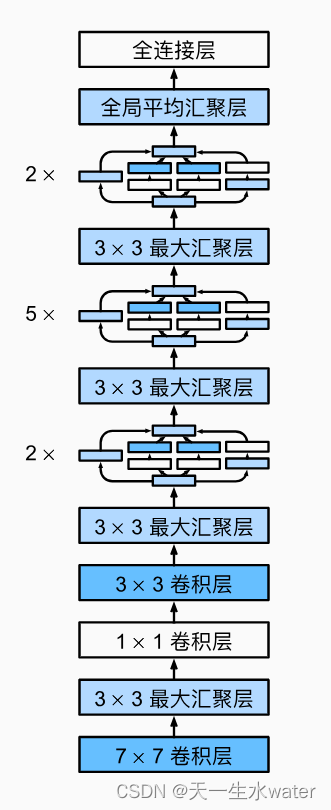
用pytorch实现google net

GoogleNet&#xff08;也称为Inception v1&#xff09;是由Google在2014年提出的一个深度卷积神经网络架构。它在ImageNet Large Scale Visual Recognition Challenge (ILSVRC) 2014比赛中取得了优秀的成绩&#xff0c;并引起了广泛的关注。 GoogleNet的设计目标是构建一个更…...

编程日记 2023/8/19 5:45:37

2023-8-15差分矩阵

题目链接&#xff1a;差分矩阵 #include <iostream>using namespace std;const int N 1010;int n, m, q; int a[N][N], b[N][N];void insert(int x1, int y1, int x2, int y2, int c) {b[x1][y1] c;b[x1][y2 1] - c;b[x2 1][y1] - c;b[x2 1][y2 1] c; }int main…...

编程日记 2023/8/19 5:44:36

物理公式分类

(99 封私信 / 81 条消息) 定义式和决定式有什么区别&#xff0c;怎么区分&#xff1f; - 知乎 (zhihu.com) 1、首先&#xff0c;定义一个物理符号&#xff08;物理量&#xff09;来表征物理世界最直观/最基本的物理现象&#xff0c;例如&#xff0c;长度&#xff08;米&#xf…...

编程日记 2023/8/19 5:43:35

vue实现登录注册

目录 一、登录页面 二、注册页面 三、配置路由 一、登录页面 <template><div class"login_container" style"background-color: rgb(243,243,243);height: 93.68vh;background-image: url(https://ts1.cn.mm.bing.net/th/id/R-C.f878c96c4179c501a6…...

编程日记 2023/8/19 5:42:34

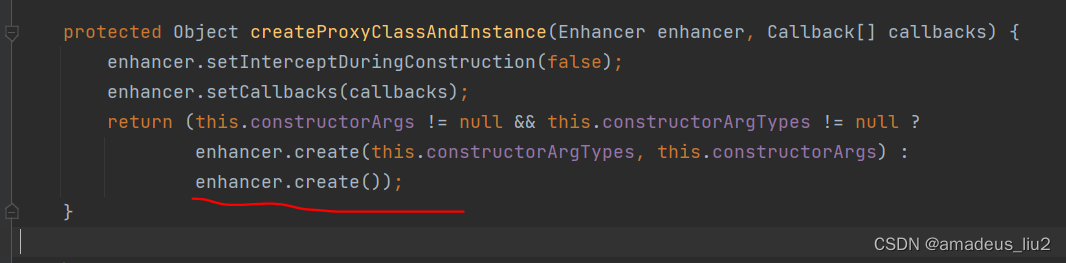
SpringBoot复习：（55）在service类中的方法上加上@Transactional注解后，Spring底层是怎么生成代理对象的？

SpringBoot run方法代码如下&#xff1a; 可以看到它会调用refreshContext方法来刷新Spring容器&#xff0c;这个refreshContext方法最终会调用AbstractApplicationContext的refresh方法&#xff0c;代码如下 如上图&#xff0c;refresh方法最终会调用finisheBeanFactoryInit…...

编程日记 2023/8/19 5:41:33

常用的图像校正方法

在数字图像处理中&#xff0c;常用的校正方法包括明场均匀性校正、查找表&#xff08;LUT&#xff09;校正和伽玛&#xff08;Gamma&#xff09;校正。这些校正方法分别针对不同的图像问题&#xff0c;可以改善图像质量&#xff0c;提升图像的可读性和可分析性。下面是这三种校…...

编程日记 2023/8/19 5:40:32

AWS security 培训笔记

云计算的好处 Amazon S3 (Storage) Amazon EC2 (Compute) 上图aws 的几个支柱&#xff1a;安全是其中一个啦 其中安全有几个方面 IAMdetection基础架构保护数据保护应急响应 关于云供应商的责任 data center 原来长这样 &#xff0c;据说非常之隐蔽的 如果有天退役了&#xf…...

编程日记 2023/8/19 5:39:30

设计模式之代理模式（Proxy）的C++实现

1、代理模式的提出 在组件的开发过程中&#xff0c;有些对象由于某种原因&#xff08;比如对象创建的开销很大&#xff0c;或者对象的一些操作需要做安全控制&#xff0c;或者需要进程外的访问等&#xff09;&#xff0c;会使Client使用者在操作这类对象时可能会存在问题&…...

编程日记 2023/8/19 5:38:29

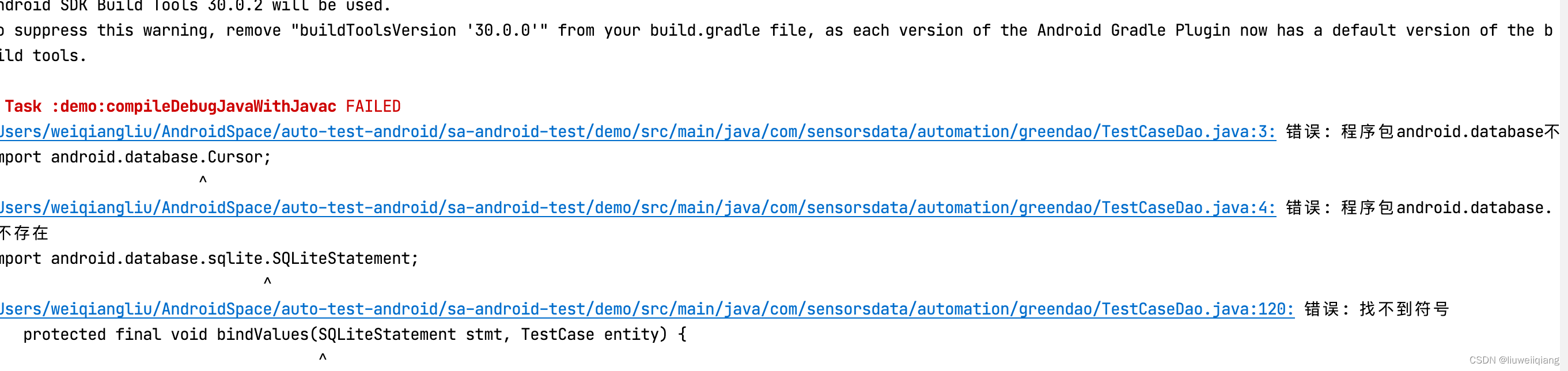
vim 配置环境变量与 JDK 编译器异常

vim 配置环境变量 使用 vim 打开系统中的配置信息&#xff08;不存在将会创建&#xff09;&#xff1a; vim ~/.bash_profile 以配置两个版本 JDK 为例&#xff08;前提是已安装 JDK&#xff09;,使用上述命令打开配置信息&#xff1a; 输入法调成英文&#xff0c;输入 i&…...

编程日记 2023/8/19 5:37:28

TiDB v7.1.0 跨业务系统多租户解决方案

本文介绍了 TiDB 数据库的资源管控技术&#xff0c;并通过业务测试验证了效果。资源管控技术旨在解决多业务共用一个集群时的资源隔离和负载问题&#xff0c;通过资源组概念&#xff0c;可以限制不同业务的计算和 I/O 资源&#xff0c;实现资源隔离和优先级调度&#xff0c;提高…...

编程日记 2023/8/19 5:36:27

【题解】二叉树中和为某一值的路径(一)

二叉树中和为某一值的路径(一) 题目链接&#xff1a;二叉树中和为某一值的路径(一) 解题思路1&#xff1a;递归 我们或许想记录下每一条从根节点到叶子节点的路径&#xff0c;计算出该条路径的和&#xff0c;但此种思路用递归稍麻烦&#xff0c;我们可以试着把和转换为差&am…...

编程日记 2023/8/19 5:35:26

css中变量和使用变量和运算

变量&#xff1a; 语法&#xff1a;--css变量名&#xff1a;值&#xff1b; --view-theme: #1a99fb; css使用变量&#xff1a; 语法&#xff1a;属性名&#xff1a;var( --css变量名 )&#xff1b; color: var(--view-theme); css运算&#xff1a; 语法&#xff1a;属性名…...

编程日记 2023/8/19 5:34:25

数据结构之线性表的类型运用Linear Lists: 数组，栈，队列，链表

线性表 定义 一个最简单&#xff0c;最基本的数据结构。一个线性表由多个相同类型的元素穿在一次&#xff0c;并且每一个元素都一个前驱&#xff08;前一个元素&#xff09;和后继&#xff08;后一个元素&#xff09;。 线性表的类型 常见的类型&#xff1a;数组、栈、队列…...

编程日记 2023/8/19 5:33:24

成瘾机制中微生物群的神秘角色

谷禾健康 成瘾是一种大脑疾病&#xff0c;受害者无法控制地对某种物质或行为产生强烈的依赖和渴求&#xff0c;尽管这种行为会产生有害的后果。成瘾包括一系列物质滥用障碍&#xff0c;例如药物、酒精、香烟&#xff0c;过度饮食。近年来&#xff0c;吸毒成瘾急剧上升&#xff…...

编程日记 2023/8/19 5:32:23

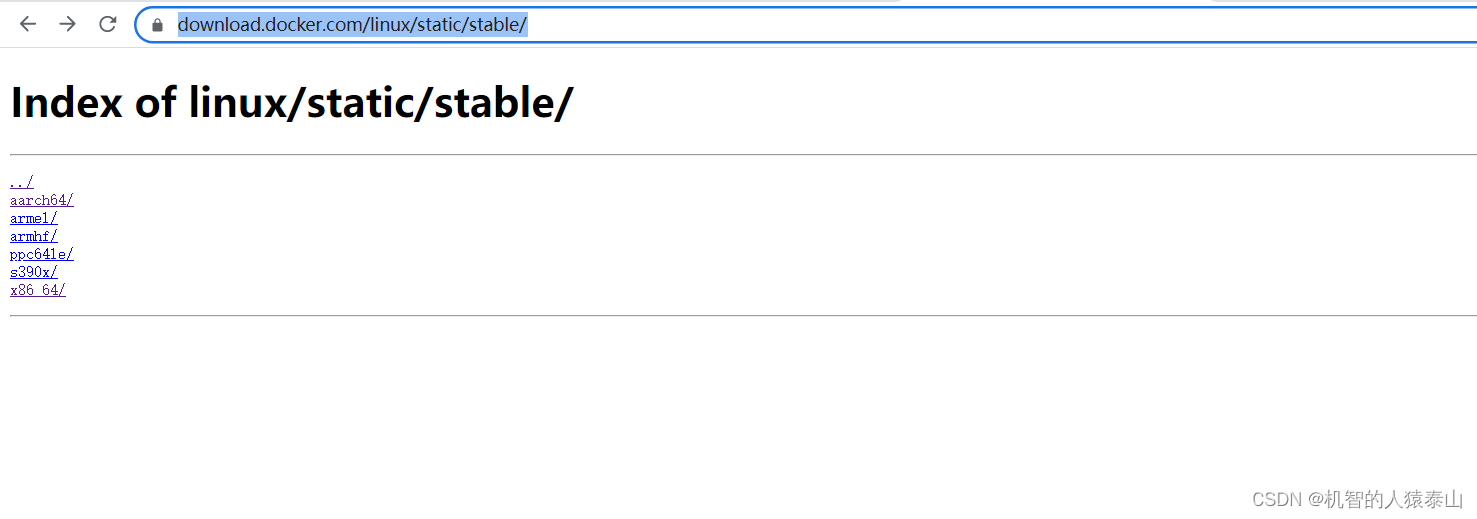
arm安装docker与docker-copose

一、银河麒麟Arm64安装docker 1、docker 安装包地址&#xff1a; https://download.docker.com/linux/static/stable 2、解压&#xff0c;然后将docker目录下文件拷贝到/usr/bin里 tar -xf docker-18.09.3.tgz mv docker/* /usr/bin/ 3、准备 docker.service系统配置文件 &…...

编程日记 2023/8/19 5:31:22

内存分配函数malloc kmalloc vmalloc

内存分配函数malloc kmalloc vmalloc malloc实现步骤： 1）请求大小调整：首先，malloc 需要调整用户请求的大小，以适应内部数据结构（例如，可能需要存储额外的元数据）。通常，这包括对齐调整，确保分配的内存地址满足特定硬件要求（如对齐到8字节或16字节边界）。 2）空闲…...

编程新知 2025/11/1 5:21:39

Xshell远程连接Kali（默认 | 私钥）Note版

前言:xshell远程连接&#xff0c;私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

编程新知 2026/1/28 2:18:42

基础测试工具使用经验

背景 vtune&#xff0c;perf, nsight system等基础测试工具&#xff0c;都是用过的&#xff0c;但是没有记录&#xff0c;都逐渐忘了。所以写这篇博客总结记录一下&#xff0c;只要以后发现新的用法&#xff0c;就记得来编辑补充一下 perf 比较基础的用法&#xff1a; 先改这…...

编程新知 2025/11/22 7:38:58

[10-3]软件I2C读写MPU6050 江协科技学习笔记（16个知识点）

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

编程新知 2026/1/28 8:34:48

Module Federation 和 Native Federation 的比较

前言 Module Federation 是 Webpack 5 引入的微前端架构方案&#xff0c;允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

编程新知 2026/1/31 13:48:37

WordPress插件：AI多语言写作与智能配图、免费AI模型、SEO文章生成

厌倦手动写WordPress文章&#xff1f;AI自动生成&#xff0c;效率提升10倍&#xff01; 支持多语言、自动配图、定时发布&#xff0c;让内容创作更轻松&#xff01; AI内容生成 → 不想每天写文章&#xff1f;AI一键生成高质量内容&#xff01;多语言支持 → 跨境电商必备&am…...

编程新知 2026/1/30 17:24:20

CMake 从 GitHub 下载第三方库并使用

有时我们希望直接使用 GitHub 上的开源库，而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例，演示如何： 使用 FetchContent 从 GitH…...

编程新知 2026/2/1 3:19:54

【JavaWeb】Docker项目部署

引言 之前学习了Linux操作系统的常见命令&#xff0c;在Linux上安装软件&#xff0c;以及如何在Linux上部署一个单体项目&#xff0c;大多数同学都会有相同的感受&#xff0c;那就是麻烦。 核心体现在三点&#xff1a; 命令太多了&#xff0c;记不住 软件安装包名字复杂&…...

编程新知 2026/2/4 16:07:02

蓝桥杯3498 01串的熵

问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798&#xff0c; 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

编程新知 2026/2/6 2:05:50

Xen Server服务器释放磁盘空间

disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

编程新知 2025/11/19 6:04:18