广度优先遍历与最短路径(Java 实例代码源码包下载)
目录
广度优先遍历与最短路径
Java 实例代码
src/runoob/graph/ShortestPath.java 文件代码:
广度优先遍历与最短路径
广度优先遍历从某个顶点 v 出发,首先访问这个结点,并将其标记为已访问过,然后顺序访问结点v的所有未被访问的邻接点 {vi,..,vj} ,并将其标记为已访问过,然后将 {vi,...,vj} 中的每一个节点重复节点v的访问方法,直到所有结点都被访问完为止。
我们可以分为三个步骤:
- (1)使用一个辅助队列 q,首先将顶点 v 入队,将其标记为已访问,然后循环检测队列是否为空。
- (2)如果队列不为空,则取出队列第一个元素,并将与该元素相关联的所有未被访问的节点入队,将这些节点标记为已访问。
- (3)如果队列为空,则说明已经按照广度优先遍历了所有的节点。
下图所示,右边蓝色表示从 0 开始遍历节点的顺序,下面是记录距离 0 的距离,可知广度优先遍历能求出无权图的最短路径。
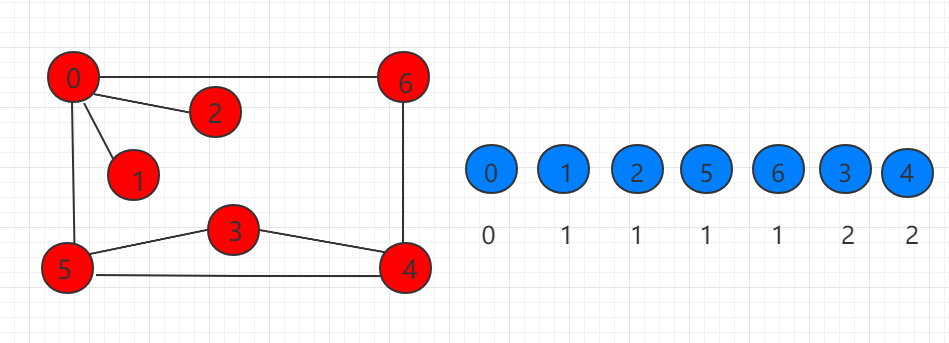
下面用代码展示如何用广度优先遍历方式完成遍历,并且查询到最短路径。我们在上一小节代码的基础上增加一全局变量 ord 数组,记录路径中节点的次序。ord[i] 表示 i 节点在路径中的次序。同时构造函数做出相应调整,在遍历相邻节点时 每访问一个未被访问的节点进行 ord[i] = ord[v] + 1记录距离。邻接表的广度优先遍历时间复杂度为 O(V+E),邻接矩阵的时间复杂度为O(V^2)。
...
// 构造函数, 寻路算法, 寻找图graph从s点到其他点的路径
public ShortestPath(Graph graph, int s){
// 算法初始化
G = graph;
assert s >= 0 && s < G.V();
visited = new boolean[G.V()];
from = new int[G.V()];
ord = new int[G.V()];
for( int i = 0 ; i < G.V() ; i ++ ){
visited[i] = false;
from[i] = -1;
ord[i] = -1;
}
this.s = s;
// 无向图最短路径算法, 从s开始广度优先遍历整张图
LinkedList<Integer> q = new LinkedList<Integer>();
q.push( s );
visited[s] = true;
ord[s] = 0;
while( !q.isEmpty() ){
int v = q.pop();
for( int i : G.adj(v) )
if( !visited[i] ){
q.push(i);
visited[i] = true;
from[i] = v;
ord[i] = ord[v] + 1;
}
}
}
...
查看从 s 点到 w 点的最短路径长度,若从 s 到 w 不可达,返回-1。
...
public int length(int w){
assert w >= 0 && w < G.V();
return ord[w];
}
...
Java 实例代码
源码包下载:Download
src/runoob/graph/ShortestPath.java 文件代码:
package runoob.graph;
import runoob.graph.read.Graph;
import java.util.LinkedList;
import java.util.Stack;
import java.util.Vector;
/**
* 广度优先遍历与最短路径
*/
public class ShortestPath {
// 图的引用
private Graph G;
// 起始点
private int s;
// 记录dfs的过程中节点是否被访问
private boolean[] visited;
// 记录路径, from[i]表示查找的路径上i的上一个节点
private int[] from;
// 记录路径中节点的次序。ord[i]表示i节点在路径中的次序。
private int[] ord;
// 构造函数, 寻路算法, 寻找图graph从s点到其他点的路径
public ShortestPath(Graph graph, int s){
// 算法初始化
G = graph;
assert s >= 0 && s < G.V();
visited = new boolean[G.V()];
from = new int[G.V()];
ord = new int[G.V()];
for( int i = 0 ; i < G.V() ; i ++ ){
visited[i] = false;
from[i] = -1;
ord[i] = -1;
}
this.s = s;
// 无向图最短路径算法, 从s开始广度优先遍历整张图
LinkedList<Integer> q = new LinkedList<Integer>();
q.push( s );
visited[s] = true;
ord[s] = 0;
while( !q.isEmpty() ){
int v = q.pop();
for( int i : G.adj(v) )
if( !visited[i] ){
q.push(i);
visited[i] = true;
from[i] = v;
ord[i] = ord[v] + 1;
}
}
}
// 查询从s点到w点是否有路径
public boolean hasPath(int w){
assert w >= 0 && w < G.V();
return visited[w];
}
// 查询从s点到w点的路径, 存放在vec中
public Vector<Integer> path(int w){
assert hasPath(w) ;
Stack<Integer> s = new Stack<Integer>();
// 通过from数组逆向查找到从s到w的路径, 存放到栈中
int p = w;
while( p != -1 ){
s.push(p);
p = from[p];
}
// 从栈中依次取出元素, 获得顺序的从s到w的路径
Vector<Integer> res = new Vector<Integer>();
while( !s.empty() )
res.add( s.pop() );
return res;
}
// 打印出从s点到w点的路径
public void showPath(int w){
assert hasPath(w) ;
Vector<Integer> vec = path(w);
for( int i = 0 ; i < vec.size() ; i ++ ){
System.out.print(vec.elementAt(i));
if( i == vec.size() - 1 )
System.out.println();
else
System.out.print(" -> ");
}
}
// 查看从s点到w点的最短路径长度
// 若从s到w不可达,返回-1
public int length(int w){
assert w >= 0 && w < G.V();
return ord[w];
}
}
相关文章:

广度优先遍历与最短路径(Java 实例代码源码包下载)
目录 广度优先遍历与最短路径 Java 实例代码 src/runoob/graph/ShortestPath.java 文件代码: 广度优先遍历与最短路径 广度优先遍历从某个顶点 v 出发,首先访问这个结点,并将其标记为已访问过,然后顺序访问结点v的所有未被访问…...
 创建UDR外部函数)
南大通用数据库(Gbase 8s) 创建UDR外部函数
一、在使用 date_format、from_unixtime、to_days、yearweek 函数时,Gbase 8s 数据库不支持,可以使用创建 UDR 外部函数来实现 二、登录命令控制台或者使用 navicat 连接 Gbase 数据库 这里使用 navicat ,点击新增连接选择 PostGreSql 驱动…...
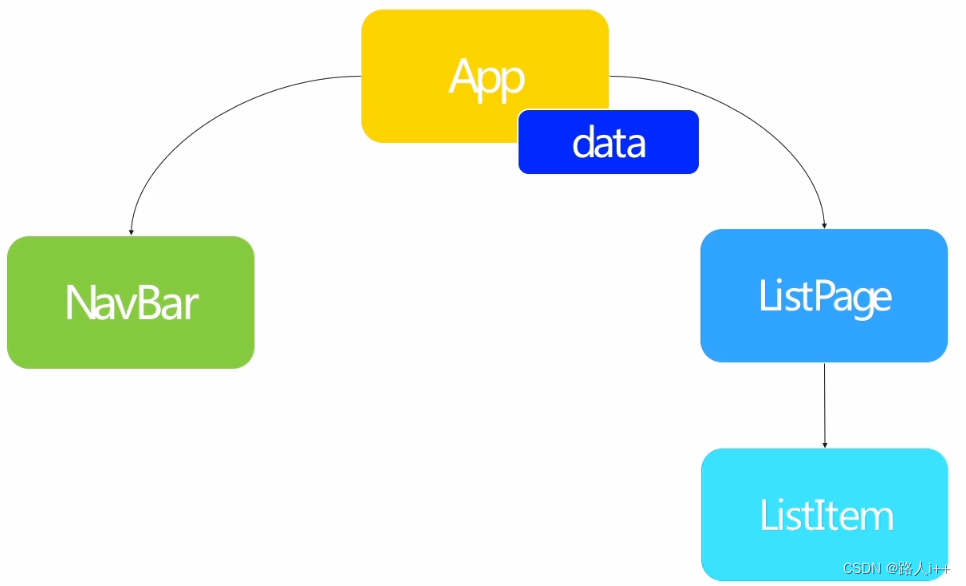
步入React正殿 - State进阶
目录 扩展学习资料 State进阶知识点 状态更新扩展 shouldComponentUpdate PureComponent 为何使用不变数据【保证数据引用不会出错】 单一数据源 /src/App.js /src/components/listItem.jsx 状态提升 /src/components/navbar.jsx /src/components/listPage.jsx src/A…...
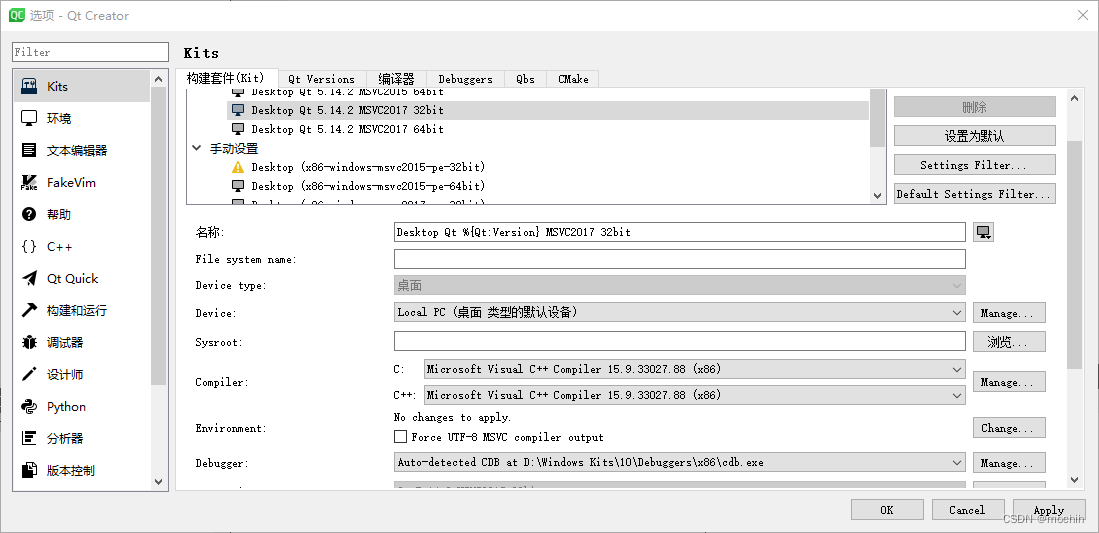
【QT+ffmpeg】QT+ffmpeg 环境搭建
1.qt下载地址 download.qt.io/archive/ 2. win10sdk 下载 https://developer.microsoft.com/en-us/windows/downloads/windows-sdk/ 安装 debug工具路径 qtcreater会自动识别 调试器选择...

责任链模式解决多个ifelse问题
责任链定义 责任链模式(Chain of Responsibility Pattern)是一种行为型设计模式,它允许多个对象按照顺序处理请求,直到其中一个对象能够处理该请求为止。 在责任链模式中,通常有一个抽象处理者(Handler&a…...

Lnton羚通关于PyTorch的保存和加载模型基础知识
SAVE AND LOAD THE MODEL (保存和加载模型) PyTorch 模型存储学习到的参数在内部状态字典中,称为 state_dict, 他们的持久化通过 torch.save 方法。 model models.shufflenet_v2_x0_5(pretrainedTrue) torch.save(model, "../../data/ShuffleNetV2_X0.5.pth…...
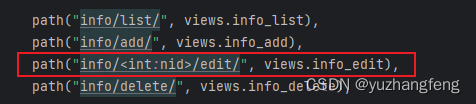
python+django+mysql项目实践四(信息修改+用户登陆)
python项目实践 环境说明: Pycharm 开发环境 Django 前端 MySQL 数据库 Navicat 数据库管理 用户信息修改 修改用户信息需要显示原内容,进行修改 通过url传递编号 urls views 修改内容需要用数据库的更新,用update进行更新,用filter进行选择 输入参数多nid,传递要修…...

sCrypt编程马拉松于8月13日在复旦大学成功举办
继6月在英国Exeter大学成功举办了为期一周的区块链编程马拉松后,美国sCrypt公司创始人兼CEO刘晓晖博士带领核心团队成员王一强、郑宏锋、周全,于8月13日在复旦大学再次成功举办了一场全新的sCrypt编程马拉松。 本次活动由上海可一澈科技有限公司与复旦大…...

Selenium手动和自动两种方式启动Chrome驱动
1. 自动启动chrome驱动(已经安装了Selenium库和Chrome驱动) 要使用Selenium自动跟随自带的Chrome驱动,你需要首先确保你已经安装了Selenium库和Chrome驱动。然后,你可以按照以下步骤进行操作: 导入必要的库: from selenium imp…...

《PostgreSQL 开发指南》第32篇 物化视图
物化视图概述 物化视图(Materialized View)是 PostgreSQL 提供的一个扩展功能,它是介于视图和表之间的一种对象。 物化视图和视图的最大区别是它不仅存储定义中的查询语句,而且可以像表一样存储数据。物化视图和表的最大区别是它…...

【RocketMQ】快速入门
文章目录 消费模式同步消息异步消息单向消息延迟消息批量消息顺序消息事务消息Tag标签和Key键Tag的使用Key的使用 首先引入rocketmq的依赖 <dependency><groupId>org.apache.rocketmq</groupId><artifactId>rocketmq-client</artifactId><ve…...

AB跳转轮询:让你的独立站收款智能化
独立站在近两年成为跨境电商的热门布局之一,特别是在亚马逊封号潮后,许多卖家开始转向独立站运营。然而,在迅速发展的同时,也不可避免地出现了一些问题,比如很多卖家的资金经常被不同程度地冻结,好不容易出…...

所有用户都能使用sudo吗
是的,Linux系统中的普通用户可以通过配置访问 sudo 命令来获得超级用户(root)权限的临时访问权。这使得普通用户可以在需要时执行需要管理员权限的操作,而无需永久性地切换到超级用户账户。 通过 sudo 命令,系统管理员…...

【广州华锐视点】VR警务教育实训系统模拟真实场景进行实践训练
随着科技的发展,虚拟现实技术在教育领域得到了广泛的应用。VR警务教育实训系统就是其中的一种应用,该系统由广州华锐互动开发,可以模拟真实的警务场景,让学生通过虚拟现实技术进行实践训练,提高学生的实践能力和技能水…...

【深入浅出C#】章节 7: 文件和输入输出操作:处理文本和二进制数据
文件和输入输出操作在计算机编程中具有重要性,因为它们涉及数据的持久化存储和交互。数据可以是不同类型的,例如文本、图像、音频、视频和二进制数据。这些不同类型的数据具有不同的存储需求。 文本数据是最常见的数据类型之一,用于存储和传输…...
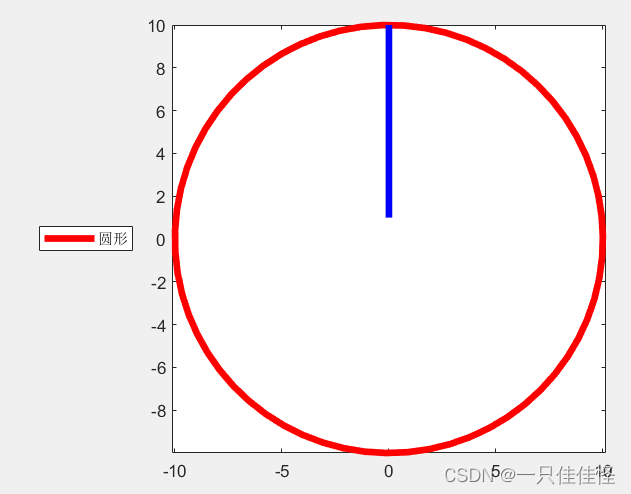
Matlab中图例的位置(图例放在图的上方、下方、左方、右方、图外面)等
一、图例默认位置 默认的位置在NorthEast r 10; a 0; b 0; t0:0.1:2.1*pi; xar*cos(t); ybr*sin(t); A1plot(x,y,r,linewidth,4);%圆 hold on axis equal A2plot([0 0],[1 10],b,linewidth,4);%直线 legend([A1,A2],圆形,line)二、通过Location对legend的位置进行改变 变…...
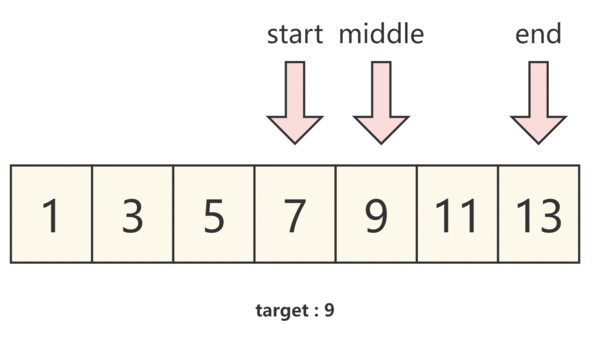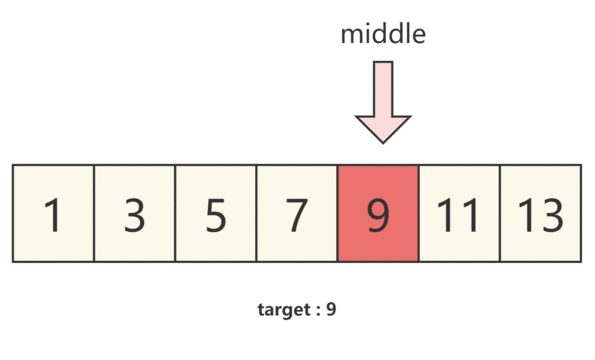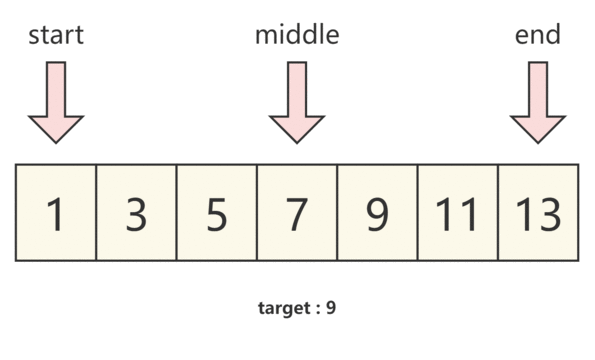
【算法学习】两数之和II - 输入有序数组
题目描述 原题链接 给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 < index1 < …...

聚观早报|京东称在技术投入没有止境;木蚁机器人完成B2轮融资
【聚观365】8月18日消息 京东零售CEO表示在技术上投入没有止境 木蚁机器人完成B2轮超亿元融资 耐能推出AI芯片KL730 三星电子泰勒晶圆厂首家客户是AI半导体厂商 韩国新能源汽车7月出口额同比大增36% 京东零售CEO表示在技术上投入没有止境 近日,京东零售CEO辛利…...
C语言:选择+编程(每日一练)
目录 选择题: 题一: 题二: 题三: 题四: 题五: 编程题: 题一:尼科彻斯定理 示例1 题二:等差数列 示例2 本人实力有限可能对一些地方解释和理解的不够清晰&…...

信道数据传输速率、码元传输速率、调制速度,信号传播速度之间的关系
1、信道数据传输速率(bit/s) 举例:移动通信中的数据传输速率。假设你的手机连接到4G网络,该网络的最大理论数据传输速率为100 Mbps。这意味着在理想情况下,你的手机可以以每秒100兆比特的速度传输数据。 2、码元传输速…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
