2023年上半年软考分数线 软考分数线公布时间
2023年上半年软考分数线:
全国标准为45分,部分地区会有省考分数线。
计算机软考的及格分数线并不是固定的,就像2016年上半年中级信息系统管理工程师考试,上午的基础知识科目及格标准是45分,下午的应用技术科目及格标准是50分。所以,计算机软考的及格分数线是会变化的。
近年来,计算机软考各专业、各级别和各科目的分数线基本稳定在45分,达到或超过这个分数即为合格。然而,软考的分数线并不是固定不变的。以2016年上半年软考中级信息系统管理工程师考试为例,上午的基础知识科目合格标准为45分,而下午的应用技术合格标准则为50分。因此,软考的分数线并非总是固定在45分。
每次计算机软考结束后,合格标准是由人事部和信息产业部发文确定的。根据全国考生的综合水平考试成绩,确定合格分数线,每年的合格分数线并不固定。合格标准在一定比例内控制,每个级别的考试科目都要达到及格才算合格。单科及格的成绩不会保留,不能在下次考试时使用。
其次,就目前全国各地区软考的分数线来看,大部分地区只有合格分数线,没有划分省合格分数线。但也有少数地区划分了省分数线,如陕西、青海等地。一般来说,软考省内分数线会比合格分数线要低。只有达到省及格分数线的考生,才能领取省软考合格证书。需要注意的是,省合格证书通常只在当地有效。
以下是陕西2023上半年软考初级分数线,大家可以参考:
陕西2023上半年软考初级分数线:
程序员基础知识:35分
程序员应用技术:35分
网络管理员基础知识:38 分
网络管理员应用技术:38分
信息处理技术员基础知识:38 分
信息处理技术员应用技术:43分
陕西2023上半年软考中级分数线:
网络工程师基础知识:35 分
网络工程师应用技术:35分
嵌入式系统设计师基础知识:43分
嵌入式系统设计师应用技术:45分
电子商务设计师基础知识:42 分
电子商务设计师应用技术:45分
系统集成项目管理工程师基础知识:38 分
系统集成项目管理工程师应用技术:38分
信息系统监理师基础知识:38 分
信息系统监理师应用技术:41分
陕西2023上半年软考高级分数线:
信息系统项目管理师基础知识:35 分
信息系统项目管理师案例分析:37分
信息系统项目管理师论文37分
系统分析师基础知识:38 分
系统分析师案例分析:41 分
系统分析师论文:41分
系统规划与管理师基础知识:39 分
系统规划与管理师案例分析:40分
系统规划与管理师论文:40分
未划定省线合格标准的科目统一执行国家合格标准。
软考分数线公布时间:
软考分数线一般会在软考成绩出来后公布。每次软考成绩查询时间都不一样,一般是在考后两个月内就能查询。
到时候,考生登录中国计算机技术职业资格网,选择当次考试时间,依次输入自己的姓名、证件号和准考证号查询成绩。
软考也可以申请成绩复查。一般来说考试成绩公布后十天内可以申请成绩复查,具体要看当地软考办的通知。复查只允许查看下午的主观考试试题,上午是客观选择题,不接受复查。
复查有错的概率比较小。查到的成绩跟自己所预估的分数相差很大,需要复核的考生,可向当地软考报名机构咨询相关成绩复核手续,填写成绩复核申请表。
相关文章:

2023年上半年软考分数线 软考分数线公布时间
2023年上半年软考分数线: 全国标准为45分,部分地区会有省考分数线。 计算机软考的及格分数线并不是固定的,就像2016年上半年中级信息系统管理工程师考试,上午的基础知识科目及格标准是45分,下午的应用技术科目及格标…...

centos7的flink安装过程
安装步骤 下载flink的tar.gz包修改flink的conf配置下载需要的lib包 具体代码(以flink1.15为例) # 下载flink的tar.gz包 wget https://archive.apache.org/dist/flink/flink-1.15.4/flink-1.15.4-bin-scala_2.12.tgz tar -zxvf flink-1.15.4-bin-scala…...
商城-学习整理-高级-性能压测缓存问题(十一)
目录 一、基本介绍1、性能指标2、JMeter1、JMeter 安装2、JMeter 压测示例1、添加线程组2、添加 HTTP 请求3、添加监听器4、启动压测&查看分析结果 3、JMeter Address Already in use 错误解决 二、性能监控1、jvm 内存模型2、堆3、jconsole 与 jvisualvm1、jvisualvm 能干…...
)
PHP 三元 !empty 而不是评估为真或假 可用isset()
是否可以使用速记三元来检查变量是否已设置,而不是是否计算结果为零或非零? 例如,我试过: $var 0; echo (string) $var ?: (string) false ?: 2;但由于前两个表达式的计算结果均为“0”或“false”,因此显示为 2。…...
, 谁更胜一筹?)
星火大模型 VS FuncGPT(慧函数), 谁更胜一筹?
哈喽,本文即通过相近的试题,看下最近爆火的科大讯飞星火大模型和 FuncGPT(慧函数)的编码能力有何区别,给大家直观地对比。 开发过程中经常会遇到读取文件内容的情况,需要【判断文件路径是目录还是文件】&am…...

使用 Python 获取 Redis 数据库中的所有键
如果你了解 JSON,就会熟悉 Redis 设计系统。 它使用键值结构和分布式内存方法来实现弹性数据库。 哈希、列表、集合、排序集合、字符串、JSON 和流是 Redis 支持的众多数据结构之一。 这个开源数据库支持不同的语言,包括 Python,如果您正在使…...

C的进阶C++学习方向
(꒪ꇴ꒪ ),Hello我是祐言QAQ我的博客主页:C/C语言,Linux基础,ARM开发板,软件配置等领域博主🌍快上🚘,一起学习,让我们成为一个强大的攻城狮!送给自己和读者的…...

【仿写框架之仿写Tomact】二、初始化阶段加载项目中所有servlet类对象
文章目录 1、自定义MyWebServlet 注解2、创建HttpServlet文件3、加载项目中的所有以.java结尾的文件4、收集项目中带有MyWebServlet 的类对象 1、自定义MyWebServlet 注解 我们知道,tomcat是依据WebServlet注解去收集所有servlet类的。 import java.lang.annotati…...

Linux实用运维脚本分享
Linux实用运维脚本分享🍃 MySQL备份 目录备份 PING查询 磁盘IO检查 性能相关 进程相关 javadump.sh 常用工具安装 常用lib库安装 系统检查脚本 sed进阶 MySQL备份 #!/bin/bashset -eUSER"backup" PASSWORD"backup" # 数据库数据目录…...
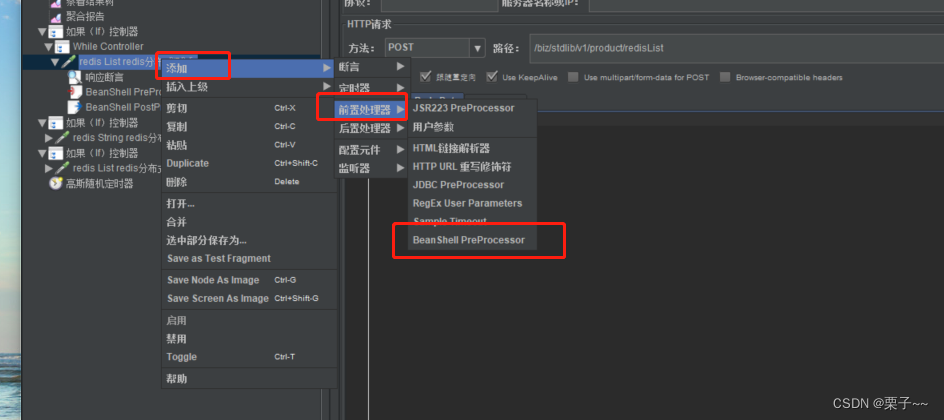
JMeter 特殊组件-逻辑控制器与BeanShell PreProcessor 使用示例
文章目录 前言JMeter 特殊组件-逻辑控制器与BeanShell PreProcessor 使用示例1. 逻辑控制器使用1.1. While Controller 使用示例1.2. 如果(If)控制器 使用示例 2. BeanShell PreProcessor 使用示例 前言 如果您觉得有用的话,记得给博主点个赞…...

时序预测 | MATLAB实现SA-ELM模拟退火算法优化极限学习机时间序列预测
时序预测 | MATLAB实现SA-ELM模拟退火算法优化极限学习机时间序列预测 目录 时序预测 | MATLAB实现SA-ELM模拟退火算法优化极限学习机时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现SA-ELM模拟退火算法优化极限学习机时间序列预测 程序设计 完整…...
Ubuntu 连接海康智能相机步骤(亲测,成功读码)
ubuntu20.04下连接海康智能相机 Ubuntu 连接海康智能相机步骤(亲测,已成功读码)输出的结果 Ubuntu 连接海康智能相机步骤(亲测,已成功读码) (就是按照海康的提供的步骤和源码连接相机,流水账) 安装Ubuntu20.04安装gcc和g,IDmvs只…...

sass笔记
声明变量 通过$标识符进行命名及引用混合器 类似vue中的函数 通过 mixin标识定义 include 标识调用& 父选择器标识extend 进行继承可嵌套可导入 通过 import 文件位置’ 、进行导入 <style> //1 声明变量 $name: 15px; $color: skyblue;mixin border-radius($num) {/…...

C/C++中volatile关键字详解
1. 为什么用volatile? C/C 中的 volatile 关键字和 const 对应,用来修饰变量,通常用于建立语言级别的 memory barrier。这是 BS 在 "The C Programming Language" 对 volatile 修饰词的说明: A volatile specifier is a hint to a…...
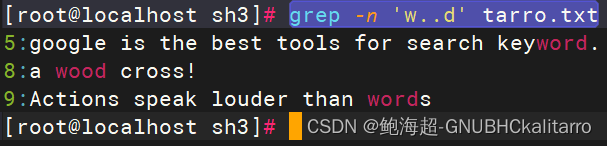
Linux:shell脚本:基础使用(4)《正则表达式-grep工具》
正则表达式定义: 使用单个字符串来描述,匹配一系列符合某个句法规则的字符串 正则表达式的组成: 普通字符串: 大小写字母,数字,标点符号及一些其他符号 元字符:在正则表达式中具有特殊意义的专用字符 正则表…...

如何建立单元测试
快速开始 zixun-quickstart-mk3生成的项目已经配置好了基础的BaseTest,各个测试类只需要继承BaseTest就可以开始进行单元测试的编写了。 如何进行Mock 为了保证独立性和可重复执行,所有的外部依赖都需要进行Mock,SpringTest引入了Mockito作为单测Mock组件, Mickito官方文…...

typeScript 接口和类
工具: PlayGround 接口 接口用来定义对象的结构和类型,描述对象应该具有哪些属性和方法。 它仅用于声明,而不是实现; 这对于编写可重用的代码非常有用。它可用于: 关键字是interface, 注意:它…...

这项与越来越多企业有关的行业标准,网易云信深度参与制定!
近日,由中国信息通信研究院主办的 2023 数字生态发展大会暨中国信通院“铸基计划”年中会议在北京召开。本次大会发布了中国信通院在行业数字化转型中的观察和实践,并发布了中国信通院在数字化转型领域的多项工作成果。大会定向邀请了来自通信、云计算、…...

C语言,malloc使用规范
malloc 是 C 语言中用于分配内存的函数。它的名称是“memory allocation”的缩写。malloc 是在 <stdlib.h> 头文件中定义的。 malloc 的基本语法是: void* malloc(size_t size); 其中 size_t是要分配的字节数。如果分配成功,malloc返回一个指向分配…...
广度优先遍历与最短路径(Java 实例代码源码包下载)
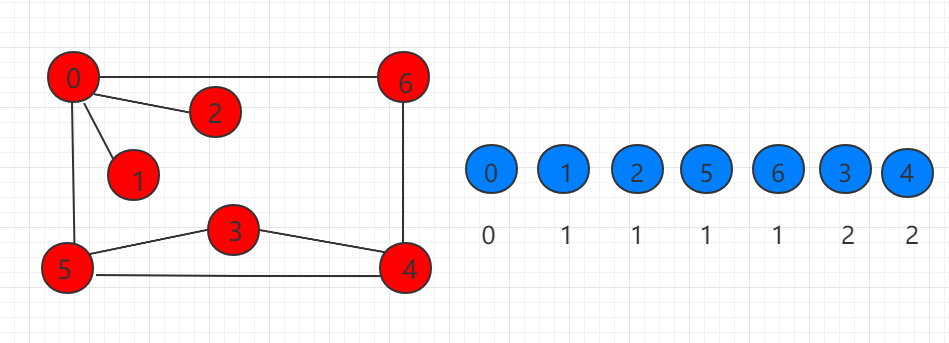
目录 广度优先遍历与最短路径 Java 实例代码 src/runoob/graph/ShortestPath.java 文件代码: 广度优先遍历与最短路径 广度优先遍历从某个顶点 v 出发,首先访问这个结点,并将其标记为已访问过,然后顺序访问结点v的所有未被访问…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
