【C++】AVL树(平衡二叉树)
目录
- 一、AVL树的定义
- 二、AVL树的作用
- 三、AVL树的插入操作
- 插入——平衡因子的更新
- 插入——左单旋
- 插入——右单旋
- 插入——左右双旋
- 插入——右左双旋
- 四、ALVL树的验证
- 五、AVL树的性能
一、AVL树的定义
AVL树,全称 平衡二叉搜索(排序)树。
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
平衡因子(Balance Factor,简写为bf)
平衡因子(bf):结点的左子树的深度减去右子树的深度。也可以是右子树的深度减去左子树的深度。看个人实现而异。
即: 结点的平衡因子 = 左子树的高度 - 右子树的高度。
或者 节点的平衡因子 = 右子树的高度 - 左子树的高度。
AVL树本质上是一颗二叉查找树,但是它又具有以下特点:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
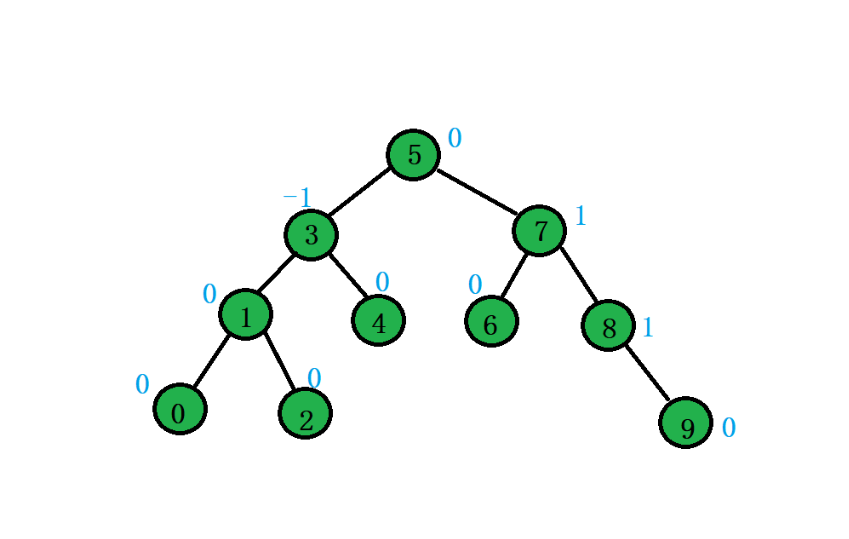
这就是一颗AVL树
二、AVL树的作用
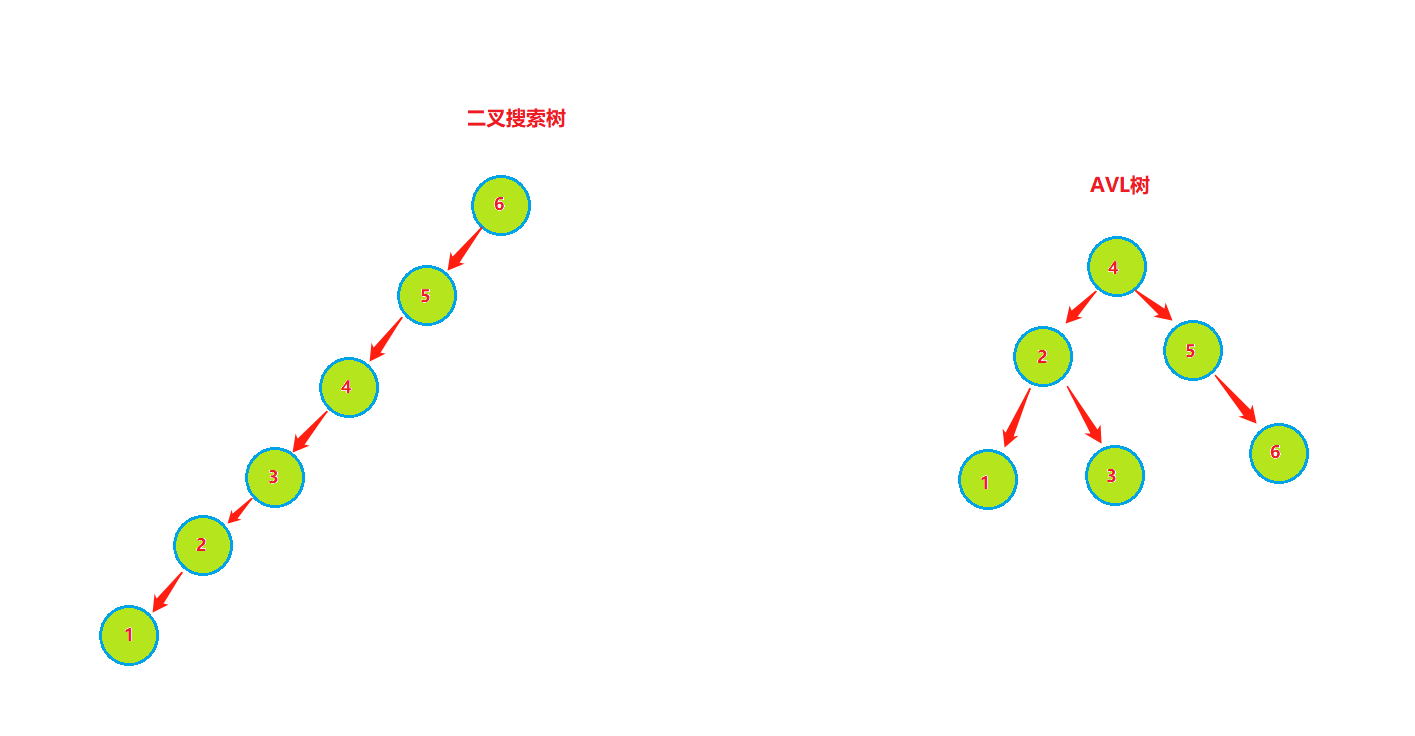
有一颗二叉树,他有n个节点,如果他是一颗二叉搜索树,他形状多样,可能会形成单枝树,高度为n,那么在这颗搜索树中查找元素的最坏时间复杂度为O(n),最好时间复杂度是O( l o g 2 n log_2 n log2n)。
如果他是一颗AVL树,他的高度稳定为 l o g 2 n log_2 n log2n,查找元素的时间复杂度为O( l o g 2 n log_2 n log2n)。
由上图可知,同样的结点,由于插入方式不同导致树的高度也有所不同。特别是在带插入结点个数很多且正序的情况下,会导致二叉树的高度是O(N),而AVL树就不会出现这种情况,树的高度始终是O(lgN).高度越小,对树的一些基本操作的时间复杂度就会越小。这也就是我们引入AVL树的原因。
三、AVL树的插入操作
插入——平衡因子的更新
在插入一个元素的时候,必然会引起平衡因子的变化,所以我们需要在插入的时候把平衡因子同时更新,在平衡因子大于1或者小于-1时,我们则需要进行旋转操作,进行调整,使平衡因子再次正常,从而保证这颗二叉树一直是一颗AVL树。
使用平衡因子计算: 右子树高度 - 左子树高度
情况一:
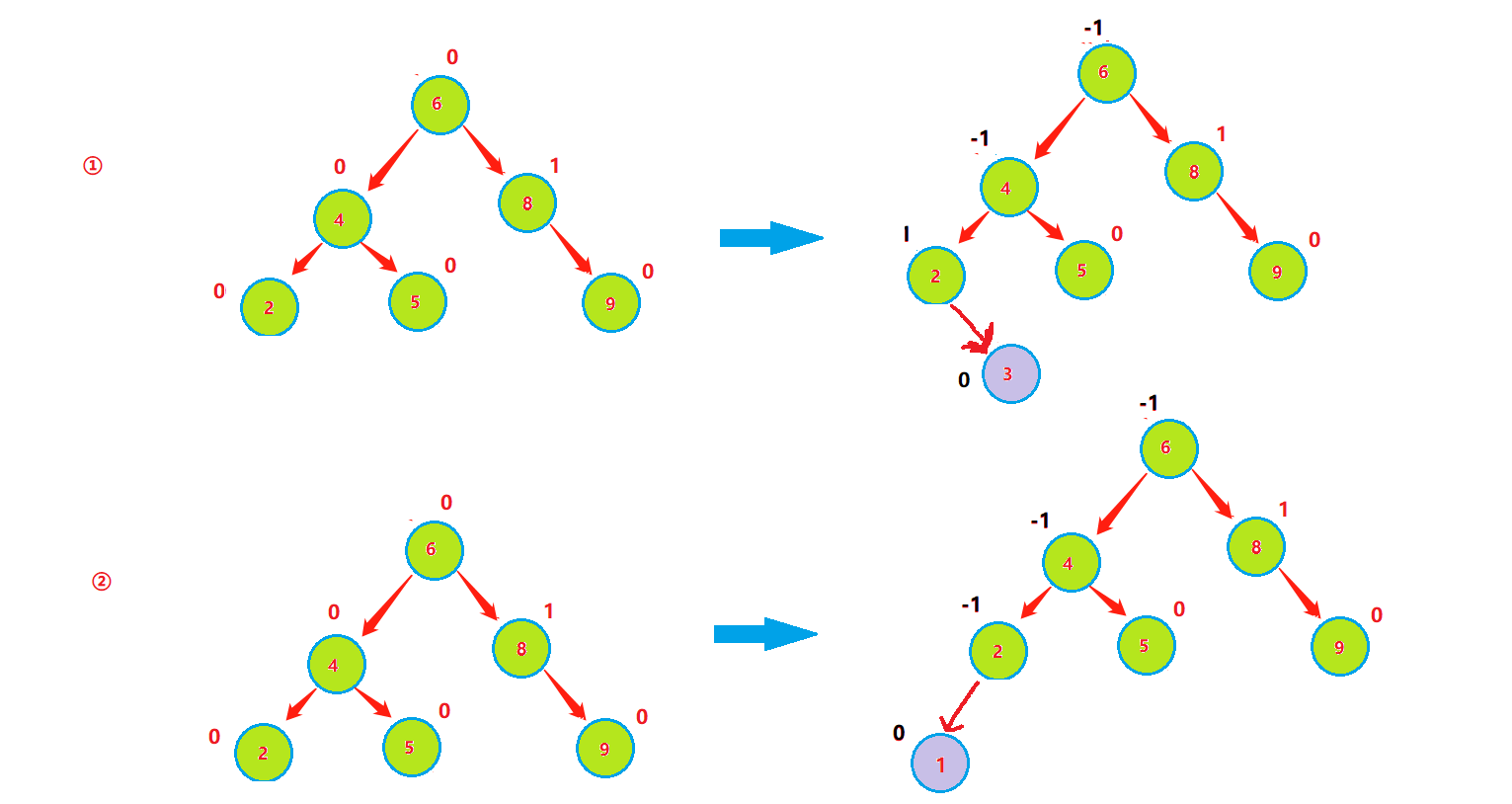
在插入元素后,需要更新父节点的平衡因子,在父节点的左子树插入元素,父节点的平衡因子-1,在父节点的左子树插入元素,父节点的平衡因子+1,如果父节点的平衡因子更新过后变为1或者-1,则需继续往上更新至根节点,因为1或者-1表示该节点的高度发生改变,需往上更新。
情况2:
在插入元素后,需要更新父节点的平衡因子,在父节点的左子树插入元素,父节点的平衡因子-1,在父节点的左子树插入元素,父节点的平衡因子+1,如果父节点的平衡因子更新过后变为0,则不需要继续向上更新,因为变为0只能说明该树高度没有变化,只是相对于原来变得平衡。
如果在更新平衡因子后,平衡因子不在(-1/0/1)范围时,则需旋转操作,下面讲解如何进行旋转操作
由于插入需要旋转的情况较多,大致可以分为四大类
插入——左单旋
动图演示
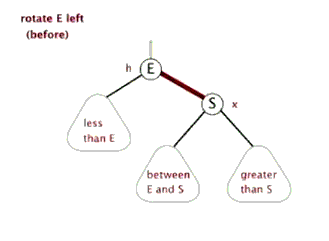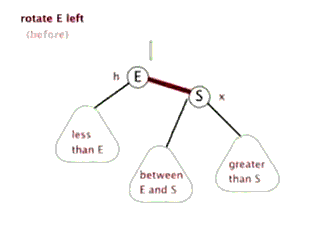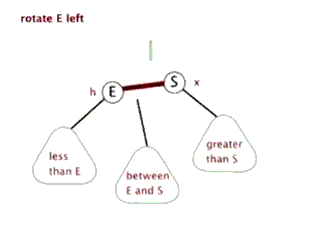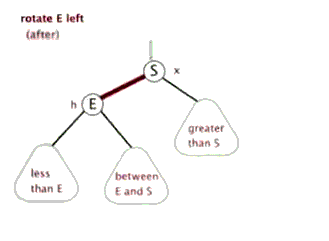
情况一
右子树高时,在右子树的右侧插入元素,此时需要左单旋
插入——右单旋
动图演示
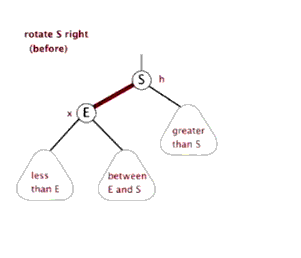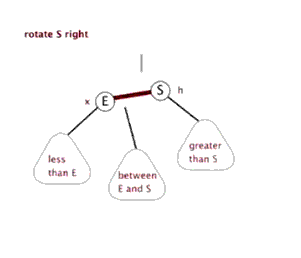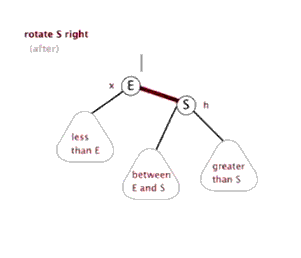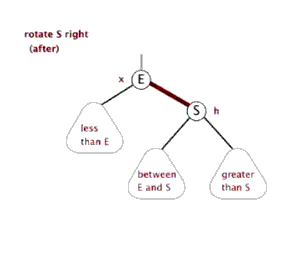
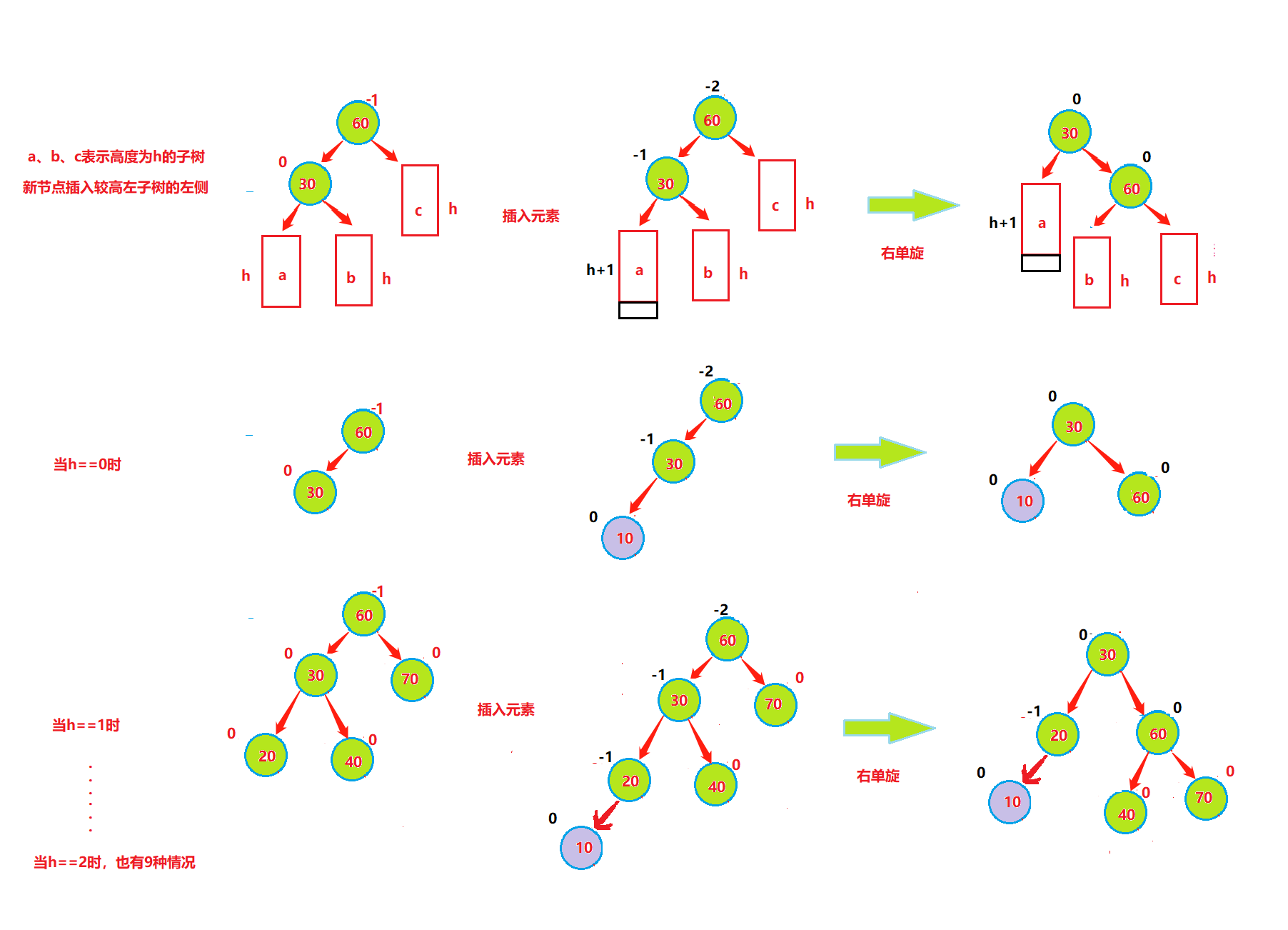
情况二、
左子树较高时,在左子树的左侧插入元素,此时需要右单旋
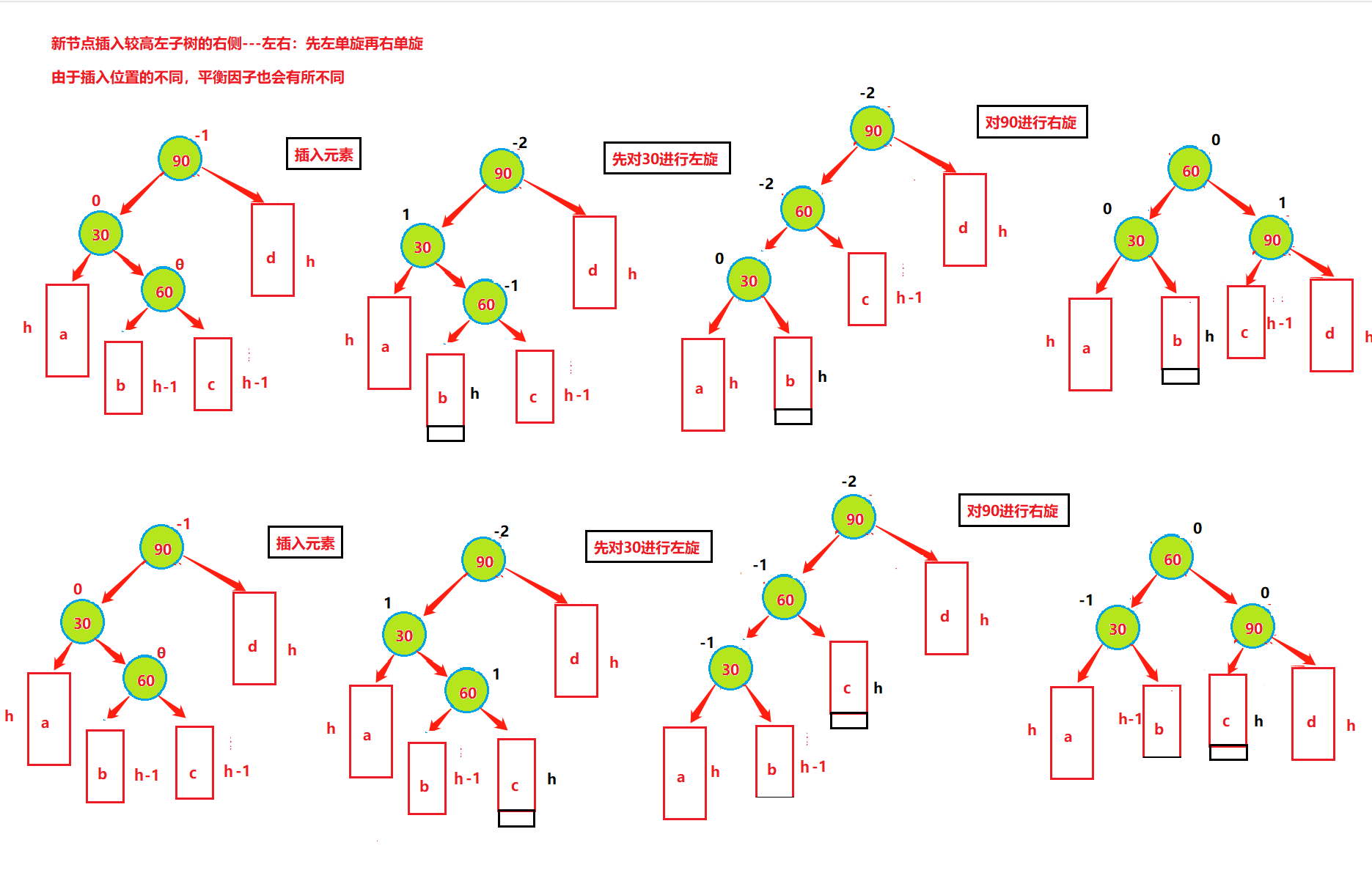
插入——左右双旋
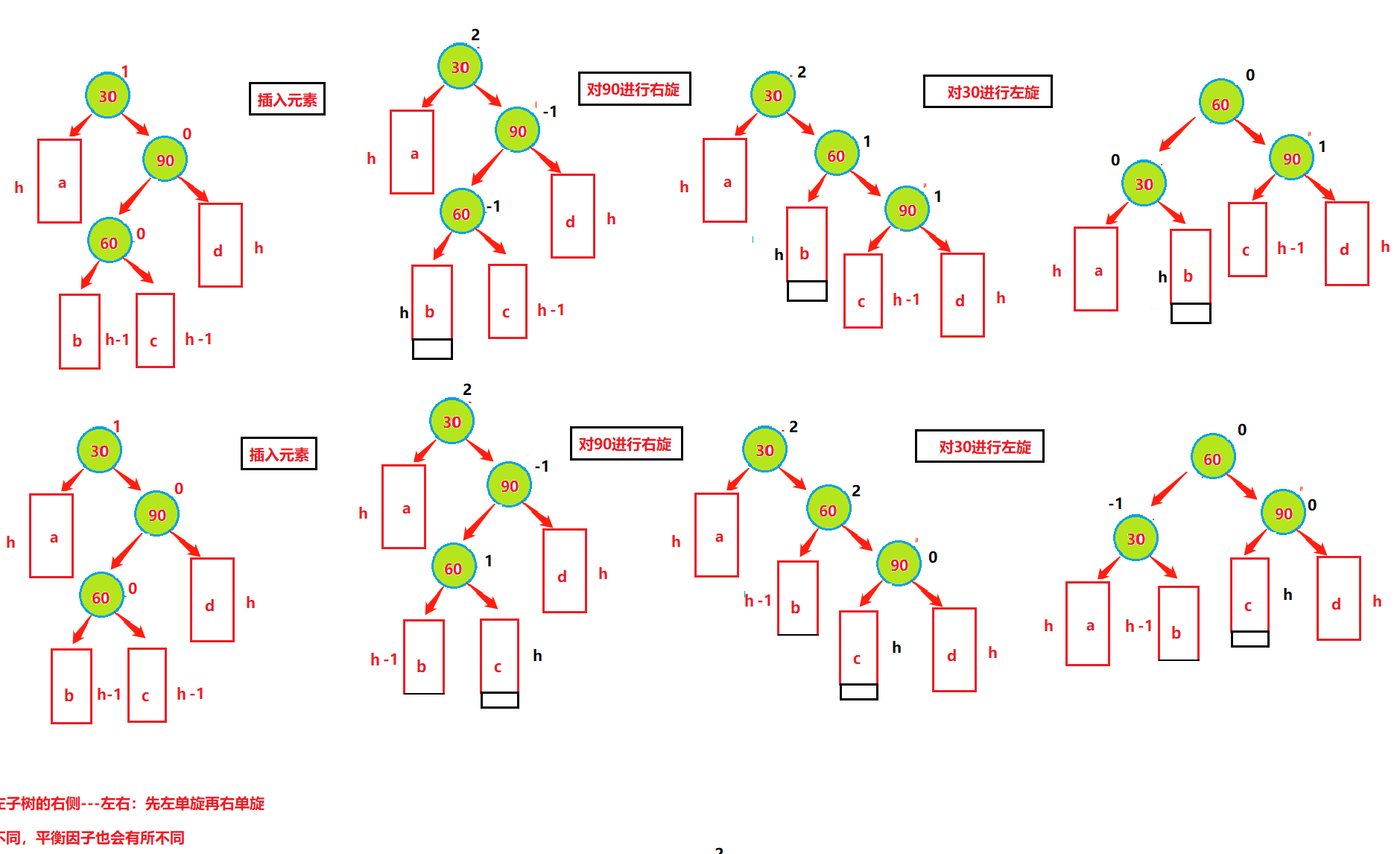
情况三、左子树较高时,在左子树的右侧插入元素,此时需要左右双旋,即:先对30进行左单旋,然后再对90进行右单旋
插入——右左双旋
情况四、右子树较高时,在右子树的左侧插入元素,此时需要右左双旋,即:先对90进行右单旋,然后再对30进行左单旋
四、ALVL树的验证
int _Height(Node* root)
{//用来计算二叉树的高度if (root == NULL)return 0;int leftH = _Height(root->_left);int rightH = _Height(root->_right);return leftH > rightH ? leftH + 1 : rightH + 1;
}bool _IsBalance(Node* root)
{if (root == NULL)return true;int leftH = _Height(root->_left);int rightH = _Height(root->_right);//检查平衡因子if (rightH - leftH != root->_bf){cout << root->_kv.first << "节点平衡因子异常" << endl;return false;}//通过计算左右子树的高度差判断这颗二叉树是否为AVL树return abs(leftH - rightH) < 2&& _IsBalance(root->_left)&& _IsBalance(root->_right);//检查高度差要检查二叉树中所有节点的左右子树的高度差
}bool IsBalance()
{return _IsBalance(_root);
}
五、AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即 l o g 2 n log_2 n log2n 。
但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
相关文章:
【C++】AVL树(平衡二叉树)
目录 一、AVL树的定义二、AVL树的作用三、AVL树的插入操作插入——平衡因子的更新插入——左单旋插入——右单旋插入——左右双旋插入——右左双旋 四、ALVL树的验证五、AVL树的性能 一、AVL树的定义 AVL树,全称 平衡二叉搜索(排序)树。 二…...

「UG/NX」Block UI 面收集器FaceCollector
✨博客主页何曾参静谧的博客📌文章专栏「UG/NX」BlockUI集合📚全部专栏「UG/NX」NX二次开发「UG/NX」BlockUI集合「VS」Visual Studio「QT」QT5程序设计「C/C+&#...

剑指Offer61.扑克牌中的顺子 C++
1、题目描述 从若干副扑克牌中随机抽 5 张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12,K为13,而大、小王为 0 ,可以看成任意数字。…...

vue实例挂载过程
以下仅为个人见解。 1.大致流程: new Vue()时会调用initMixin(Vue)将_init挂载到vue原型上;在_init()中调用$mount()方法($mount()方法也是挂载到vue原型上的)编译template模版,并生成render()函数;挂载到vm上后,会…...

【第八讲---视觉里程计2】
在图像中提取特征点并计算特征描述,非常耗时 通过计算描述子距离在不同图像中寻找特征匹配,也非常耗时 利用通过匹配点信息计算相机位姿,没什么问题 我们可以采用以下方法进行改进: 光流:通过其他方式寻找匹配点直接法…...

设置PHP的fpm的系统性能参数pm.max_children
1 介绍 PHP从Apache module换成了Fpm,跑了几天突然发现网站打不开了。 页面显示超时,检查MySQL、Redis一众服务都正常。 进入Fpm容器查看日志,发现了如下的错误信息: server reached pm.max_children setting (5), consider r…...

vue3setup标签语法 + vite + delfin 递归组件实现无限评论功能
1、 功能效果 在线预览:https://szhihao.gitee.io/comment/ gitee仓库地址:https://gitee.com/szhihao/comment 2、实现的具体技术点 根据不同的人名可以进行评论(tap切换) 对进行的评论可以无限进行回复(递归组件和…...

optee中如何开启或关闭所有中断的
我们知道在Linux Kernel中开启或关闭中断的函数是:local_irq_enable()和local_irq_disable(), 那么在optee os中是怎样做到的呢? optee中通过使用thread_mask_exceptions()和thread_unmask_exceptions()来开启或关闭中断。 thread_mask_exceptions()和thread_unmask_excepti…...
)
基于STM32+微信小程序设计的宠物投喂装置(腾讯云IOT)
一、设计需求 【1】 项目背景 社会经济的飞速发展与城市化进程的加速,城市市民家庭的封闭化和人口老龄化的情况日益突出,基于人们的情感寄托与休闲消费的需要,中国的宠物产业也悄然兴起。家庭宠物的饲养成为了城市居民生活消遣的新方式。宠物的喂养和看护往往是宠物主人最…...

2023年上半年软考分数线 软考分数线公布时间
2023年上半年软考分数线: 全国标准为45分,部分地区会有省考分数线。 计算机软考的及格分数线并不是固定的,就像2016年上半年中级信息系统管理工程师考试,上午的基础知识科目及格标准是45分,下午的应用技术科目及格标…...

centos7的flink安装过程
安装步骤 下载flink的tar.gz包修改flink的conf配置下载需要的lib包 具体代码(以flink1.15为例) # 下载flink的tar.gz包 wget https://archive.apache.org/dist/flink/flink-1.15.4/flink-1.15.4-bin-scala_2.12.tgz tar -zxvf flink-1.15.4-bin-scala…...
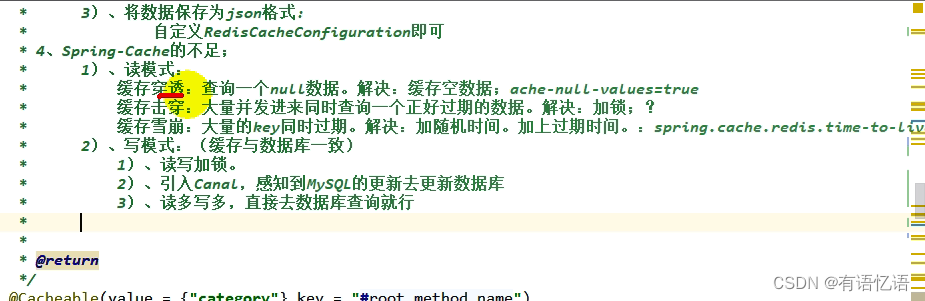
商城-学习整理-高级-性能压测缓存问题(十一)
目录 一、基本介绍1、性能指标2、JMeter1、JMeter 安装2、JMeter 压测示例1、添加线程组2、添加 HTTP 请求3、添加监听器4、启动压测&查看分析结果 3、JMeter Address Already in use 错误解决 二、性能监控1、jvm 内存模型2、堆3、jconsole 与 jvisualvm1、jvisualvm 能干…...
)
PHP 三元 !empty 而不是评估为真或假 可用isset()
是否可以使用速记三元来检查变量是否已设置,而不是是否计算结果为零或非零? 例如,我试过: $var 0; echo (string) $var ?: (string) false ?: 2;但由于前两个表达式的计算结果均为“0”或“false”,因此显示为 2。…...
, 谁更胜一筹?)
星火大模型 VS FuncGPT(慧函数), 谁更胜一筹?
哈喽,本文即通过相近的试题,看下最近爆火的科大讯飞星火大模型和 FuncGPT(慧函数)的编码能力有何区别,给大家直观地对比。 开发过程中经常会遇到读取文件内容的情况,需要【判断文件路径是目录还是文件】&am…...

使用 Python 获取 Redis 数据库中的所有键
如果你了解 JSON,就会熟悉 Redis 设计系统。 它使用键值结构和分布式内存方法来实现弹性数据库。 哈希、列表、集合、排序集合、字符串、JSON 和流是 Redis 支持的众多数据结构之一。 这个开源数据库支持不同的语言,包括 Python,如果您正在使…...

C的进阶C++学习方向
(꒪ꇴ꒪ ),Hello我是祐言QAQ我的博客主页:C/C语言,Linux基础,ARM开发板,软件配置等领域博主🌍快上🚘,一起学习,让我们成为一个强大的攻城狮!送给自己和读者的…...

【仿写框架之仿写Tomact】二、初始化阶段加载项目中所有servlet类对象
文章目录 1、自定义MyWebServlet 注解2、创建HttpServlet文件3、加载项目中的所有以.java结尾的文件4、收集项目中带有MyWebServlet 的类对象 1、自定义MyWebServlet 注解 我们知道,tomcat是依据WebServlet注解去收集所有servlet类的。 import java.lang.annotati…...

Linux实用运维脚本分享
Linux实用运维脚本分享🍃 MySQL备份 目录备份 PING查询 磁盘IO检查 性能相关 进程相关 javadump.sh 常用工具安装 常用lib库安装 系统检查脚本 sed进阶 MySQL备份 #!/bin/bashset -eUSER"backup" PASSWORD"backup" # 数据库数据目录…...
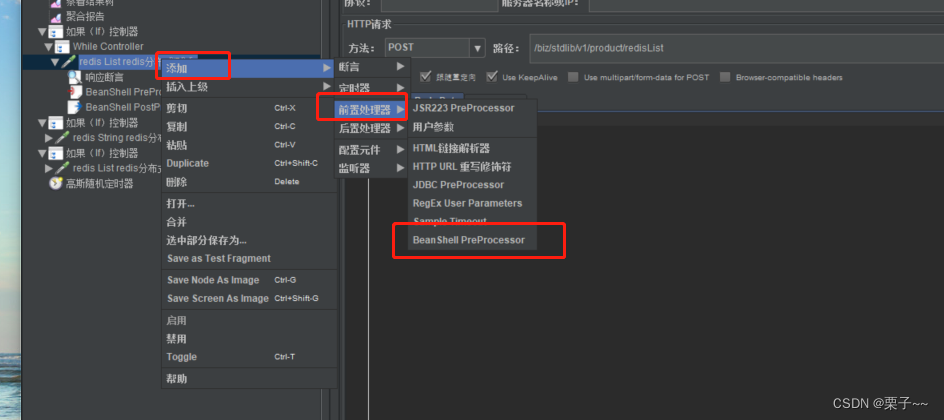
JMeter 特殊组件-逻辑控制器与BeanShell PreProcessor 使用示例
文章目录 前言JMeter 特殊组件-逻辑控制器与BeanShell PreProcessor 使用示例1. 逻辑控制器使用1.1. While Controller 使用示例1.2. 如果(If)控制器 使用示例 2. BeanShell PreProcessor 使用示例 前言 如果您觉得有用的话,记得给博主点个赞…...

时序预测 | MATLAB实现SA-ELM模拟退火算法优化极限学习机时间序列预测
时序预测 | MATLAB实现SA-ELM模拟退火算法优化极限学习机时间序列预测 目录 时序预测 | MATLAB实现SA-ELM模拟退火算法优化极限学习机时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现SA-ELM模拟退火算法优化极限学习机时间序列预测 程序设计 完整…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...