【2.19】算法题2:贪心算法、动态规划、分治
题目:给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。
方法一:贪心算法
原理:若当前指针所指元素之前的和小于0,则丢弃当前元素之前的数列。
三个变量: 前面数之和 当前数之和 最大和
int maxSubArray(int* nums, int numsSize){int preSum = 0,MaxSum = -10000,curSum = nums[0]; //初始化之前和为0,当前和为第一个元素,最大和为一个很大的负数。for(int i = 0;i < numsSize;i ++){ //遍历数组if(i==0) preSum = 0;else preSum += nums[i-1];if(preSum<0){ //如果之前和小于0,则把当前元素赋值给当前和,之前和重新变为0curSum = nums[i]; preSum = 0;}else{curSum = preSum + nums[i]; //如果之前和不小于0,则把当前元素+之前和赋值给当前和,}if(curSum>MaxSum){ //如果当前和大于最大和,则赋值给最大和MaxSum = curSum;}}return MaxSum;
}
复杂度:时间O(n),空间O(1)。
方法二:动态规划
若前一个元素大于0,则将其加到当前元素上。
int maxSubArray(int* nums, int numsSize) {int pre = 0, maxAns = nums[0]; //初始化前一个元素为0,最大子数组为0for (int i = 0; i < numsSize; i++) { //遍历数组pre = fmax(pre + nums[i], nums[i]);//返回两个数中最大的数,赋值给前一个元素maxAns = fmax(maxAns, pre);//每一个当前元素和当前最大子数组和比较}return maxAns;
}
动态规划适用场景:
能够利用动态规划算法求解的问题都会具备以下两点性质:
最优子结构: 利用动态规划算法求解问题的第一步就是需要刻画问题最优解的结构,并且如果一个问题的最优解包含其子问题的最优解,则此问题具备最优子结构的性质。因此,判断某个问题是否适合用动态规划算法,需要判断该问题是否具有最优子结构。
Tips: 最优子结构的定义主要是在于当前问题的最优解可以从子问题的最优解得出,当子问题满足最优解之后,才可以通过子问题的最优解获得原问题的最优解。
重叠子问题: 适合用动态规划算法去求解的最优化问题应该具备的第二个性质是问题的子问题空间必须足够” 小 “,也就是说原问题递归求解时会重复相同的子问题,而不是一直生成新的子问题。如果原问题的递归算法反复求解相同的子问题,我们就称该最优化问题具有重叠子问题。
Tips: 在这里,我们需要注意是,与适用动态规划算法去求解的问题具备重叠子问题性质相反,前面我们介绍的分治算法递归解决问题时,问题的子问题都是互不影响,相互独立的,这个也是我们在选用动态规划算法还是分治法解决问题时的一个判断条件。
时间复杂度:O(n),其中 n 为 nums 数组的长度。我们只需要遍历一遍数组即可求得答案。
空间复杂度:O(1)。我们只需要常数空间存放若干变量。
注:和贪心算法一样,动态规划算法只是一种思想,不是像排序算法一样有具体的代码。
方法三:分治算法
分治算法(Divide and Conquer)
将序列从中分为左右两个子序列。
递归求得两个子列的最大和。
从中分点分头向左、右两边扫描,找出跨过分界线的最大子列和。
输出这三个子列和最大的一个。
struct Status {int lSum, rSum, mSum, iSum;
};struct Status pushUp(struct Status l, struct Status r) {int iSum = l.iSum + r.iSum;int lSum = fmax(l.lSum, l.iSum + r.lSum);int rSum = fmax(r.rSum, r.iSum + l.rSum);int mSum = fmax(fmax(l.mSum, r.mSum), l.rSum + r.lSum);return (struct Status){lSum, rSum, mSum, iSum};
};struct Status get(int* a, int l, int r) {if (l == r) {return (struct Status){a[l], a[l], a[l], a[l]};}int m = (l + r) >> 1;struct Status lSub = get(a, l, m);struct Status rSub = get(a, m + 1, r);return pushUp(lSub, rSub);
}int maxSubArray(int* nums, int numsSize) {return get(nums, 0, numsSize - 1).mSum;
}
相关文章:

【2.19】算法题2:贪心算法、动态规划、分治
题目:给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。方法一:贪心算法原理:若当前指针所指元素之前的和小…...
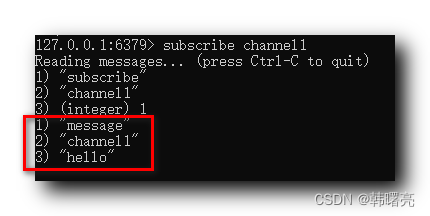
【Redis】Redis 发布订阅通信模式 ( 发布订阅模式 | 订阅频道 | 发布消息 | 接收消息 )
文章目录一、发布订阅模式二、订阅频道三、发布消息四、接收消息一、发布订阅模式 Redis 中 存在一种 发布订阅 消息通信模式 : 消息发布者 : 负责发送消息 , 订阅者需要订阅该发布者频道 ;消息订阅者 : 负责接收消息 ; 订阅者 先 订阅 发布者频道 , 当 发布者 发布消息时 , …...
VNCTF 2023复现
文章目录象棋王子电子木鱼BabyGo象棋王子 签到题,直接在源码中找就ok。 找到一处编码,在控制台输出。 flag为:flag{w3lc0m3_t0_VNCTF_2023~~~} 电子木鱼 需要先理清代码逻辑。 存在三个路由。 一:/路由用来查看当前的功德数量…...

python基础知识有哪些需要背(记住是基础知识)我是初学者
大家好,小编来为大家解答以下问题,一个有趣的事情,一个有趣的事情,今天让我们一起来看看吧! 1、python基础知识有哪些需要背(记住是基础知识)我是初学者 或看好Python的广阔前景,或…...

Linux下TCP连接断开后不释放的解决办法
问题:在开发测试时发现断开与服务器端口后再次连接时拒绝连接。 分析:服务器上查看端口占用情况,假设端口为8888。 netstat -anp |grep 8888 发现端口8888端口显示被占用(ip为本机ip确定是上次连接)且状态为ESTABLI…...

1.关于嵌入式开发软件工程师的理解
学习嵌入式软件开发,首先要学会使用工具, 包括各种语言,C语言、FPGA、C等各种工具软件,各种芯片开发的IDE环境各种操作系统,Vxworks、Linux、Freertos等计算机基础,基本的框架结构,网络通信等编…...

1760字,让你拿捏 [‘列表‘]
如约而至,紧接着第一篇文章,小编将会陆续把自己精心做的全套Python笔记依次发放给大家,便于大家学习Python、期末备考、巩固基础等(这几期是公众号小插曲,后期发放编程技术的话主要还是会围绕Java来展开,感谢小伙伴们的…...

A562基于android的养老APP
需求信息: 1:家庭信息管理,包括家庭成员基本情况、性别、年龄、关系、工作单位、联系方式(手机号码、微信等); 2:个人健康数据管理,包括姓名、性别、年龄、关系、原工作单位、联系方式(手机号码…...
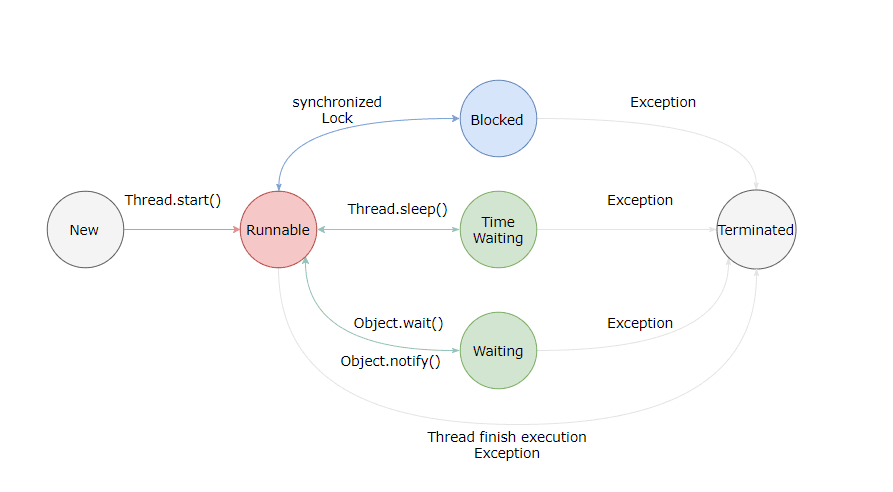
java面试题-并发基础
1.多线程的出现是要解决什么问题的? 本质什么?提高程序性能:单线程程序只能按照固定的顺序依次执行每个任务,无法同时处理多个任务。多线程技术可以在同一时间内执行多个任务,从而提高程序的运行效率和响应速度。提高程序的并发性ÿ…...

用纯C语言实现3D空间中的点坐标转化为屏幕二维点坐标,包含主视图、侧视图、俯视图、正等轴投影
要实现3D空间中的点坐标转换为屏幕二维点坐标,需要进行透视变换和投影变换。以下是一些基本的思路和示例代码,可以用于实现主视图、侧视图、俯视图、正等轴投影。 1. 主视图投影 主视图投影是指以一个点作为视点,从一个方向观察物体&#x…...

.sh脚本文件的执行方式
方法1: ./xxx.sh方法2: source xxx.sh方法3: bash xxx.sh方法4: sh xxx.sh初识shell,学习并记录...

Android 基础知识4-2.5View与VIewGroup的概念、关系与区别
1.概念: Android里的图形界面都是由View和ViewGroup以及他们的子类构成的: View:所有可视化控件的父类,提供组件描绘和时间处理方法 ViewGroup: View类的子类,可以拥有子控件,可以看作是容器 Android UI中的控件都是…...

【ESP 保姆级教程】玩转巴法云篇① ——初识巴法云
忘记过去,超越自己 ❤️ 博客主页 单片机菜鸟哥,一个野生非专业硬件IOT爱好者 ❤️❤️ 本篇创建记录 2023-02-19 ❤️❤️ 本篇更新记录 2023-02-19 ❤️🎉 欢迎关注 🔎点赞 👍收藏 ⭐️留言📝🙏 此博客均由博主单独编写,不存在任何商业团队运营,如发现错误,请…...

Python学习-----模块3.0(正则表达式-->re模块)
目录 前言: 导入模块 1.re.match() 函数 (1)匹配单个字符 (2)匹配多个字符 (3) 匹配开头和结尾 2.re.search() 函数 3.re.findall() 函数 4.re.finditer() 函数 5.re.split() 函数 6.re.sub() 函数 7.re.sub…...
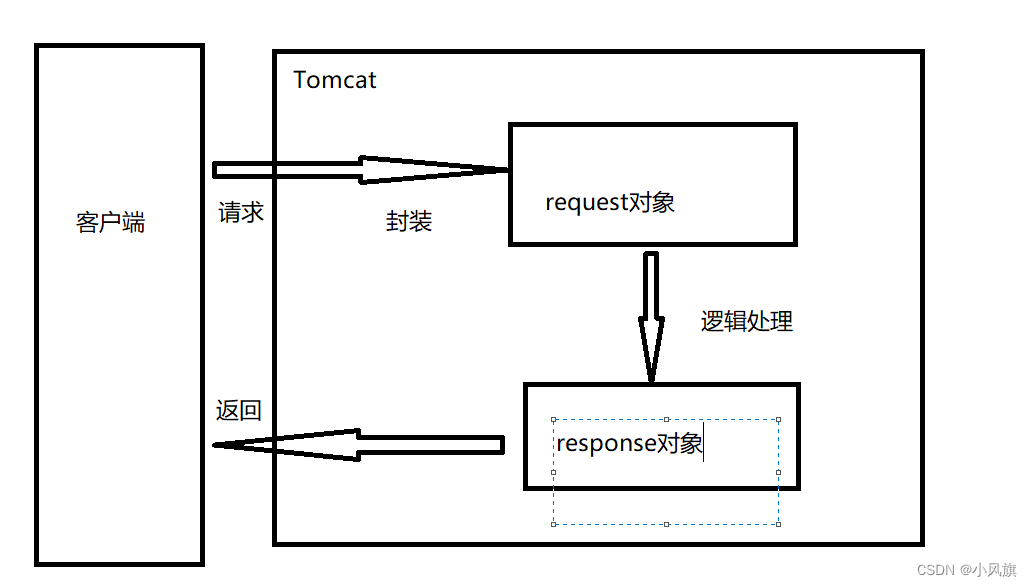
JSP中http与内置对象学习笔记
本博文讲述jsp客户端与服务器端的http、jsp内置对象与控制流和数据流实现 1.HTTP请求响应机制 HTTP协议是TCP/IP协议中的一个应用层协议,用于定义客户端与服务器之间交换数据的过程 1.1 HTTP请求 HTTP请求由请求行、消息报头、空行和请求数据4部分组成。 请求行…...
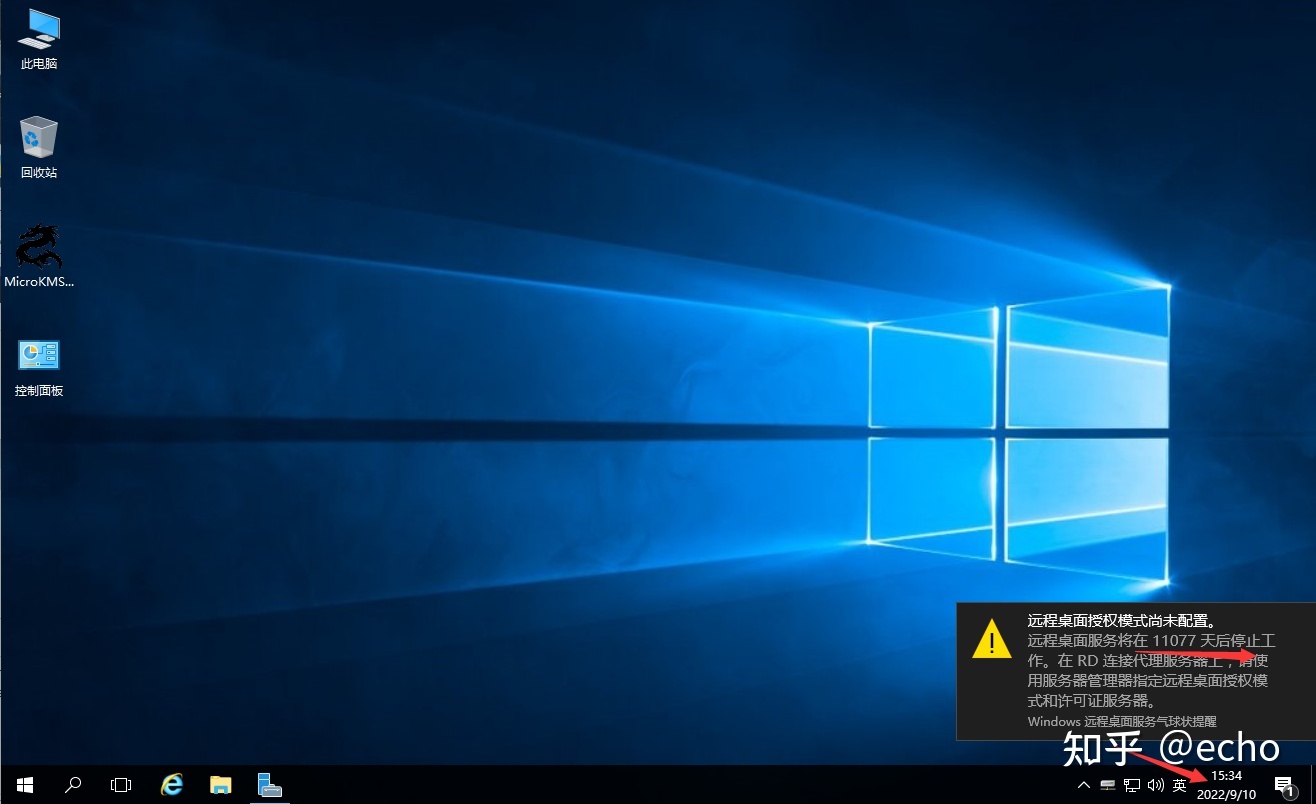
Windows Server 2016远程桌面配置全过程
镜像下载 系统镜像网址 本次下载的是 Windows Server 2016 (Updated Feb 2018) (x64) - DVD (Chinese-Simplified) 远程桌面配置 Step 1 在开始菜单搜索服务,打开服务器管理器,点击右上角的管理按钮 Step 2 添加角色控制,点击下一步 S…...
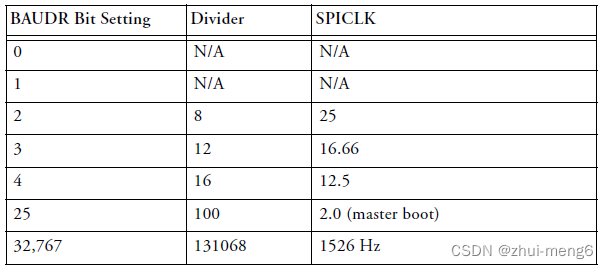
SPI通讯简介
一、基本概念 SPI是串行外设接口(Serial Peripheral Interface)的缩写,是一种高速的,全双工,同步的通信总线,主要应用在EEPROM,FLASH,实时时钟,AD转换器,多MCU间通讯等等,SPI端口可以在多主器件…...

Python 迭代器
迭代器协议 对象必须提供一个 next() 方法,执行该方法要么迭代下一项,要么就引起一个 StopIteration异常以终止迭代(只能往后不能往前)—— 迭代器协议 协议是一种约定,可迭代对象实现了迭代器协议(for、…...
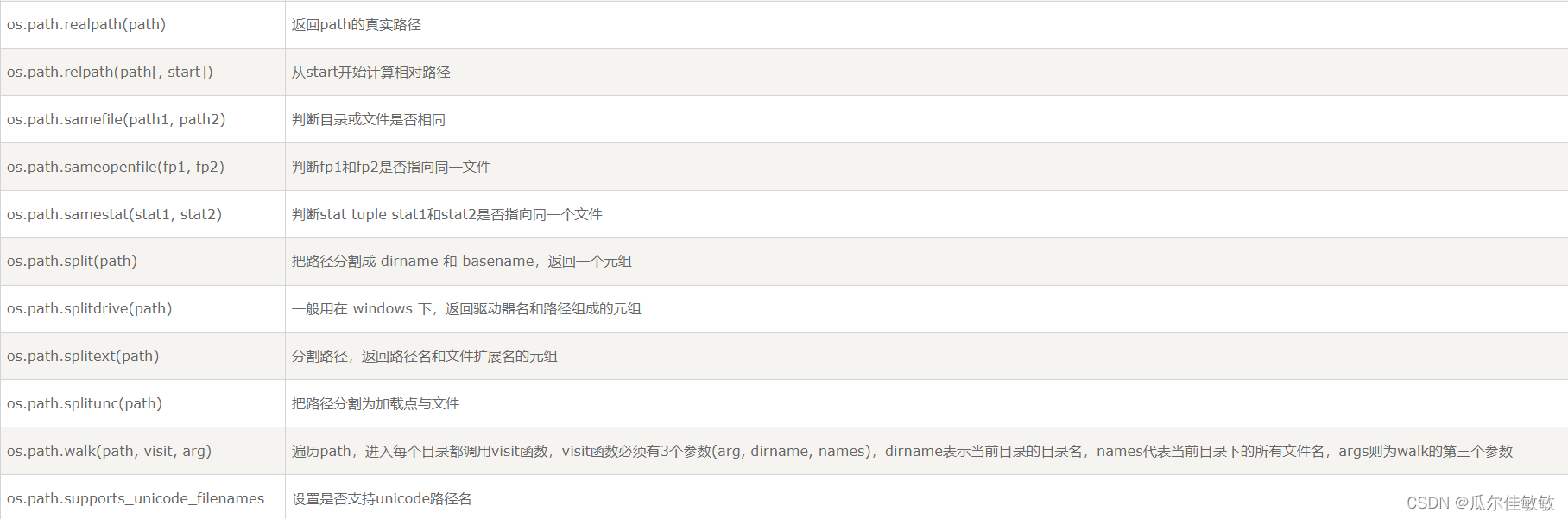
Python语言零基础入门教程(二十七)
Python OS 文件/目录方法 Python语言零基础入门教程(二十六) 61、Python os.utime() 方法 概述 os.utime() 方法用于设置指定路径文件最后的修改和访问时间。 在Unix,Windows中有效。 语法 utime()方法语法格式如下: os.uti…...

Redis基础操作以及数据类型
目录 Redis基础操作 java中的i是不是原子操作?不是 数据类型 1. list 2. set 3. Hash哈希 4. Zset有序集合 Redis基础操作 set [key] [value] 设置值 (设置相同的会将原先的覆盖) get [key] 获取值 不能覆盖和替换 ttl [key] 以秒为单…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...

React、Git、计网、发展趋势等内容——前端面试宝典(字节、小红书和美团)
React React Hook实现架构、.Hook不能在循环嵌套语句中使用 , 为什么,Fiber架构,面试向面试官介绍,详细解释 用户: React Hook实现架构、.Hook不能在循环嵌套语句中使用 , 为什么,Fiber架构,面试向面试官介绍&#x…...
