用纯C语言实现3D空间中的点坐标转化为屏幕二维点坐标,包含主视图、侧视图、俯视图、正等轴投影
要实现3D空间中的点坐标转换为屏幕二维点坐标,需要进行透视变换和投影变换。以下是一些基本的思路和示例代码,可以用于实现主视图、侧视图、俯视图、正等轴投影。
1. 主视图投影
主视图投影是指以一个点作为视点,从一个方向观察物体,投影到一个平面上。通常情况下,主视图的观察方向是从正面,也就是Z轴负方向。投影平面一般是平行于X-Y平面。
具体实现可以通过以下步骤完成:
- 定义观察点坐标和投影平面距离
- 对3D坐标进行透视变换
- 对透视变换后的坐标进行投影变换
- 将投影后的坐标映射到屏幕上
示例代码:
int x_2d = (int) (x_3d / (z_3d - view_point_z) * distance_to_projection_plane);
int y_2d = (int) (y_3d / (z_3d - view_point_z) * distance_to_projection_plane);
2. 侧视图投影
侧视图投影是指以一个点作为视点,从一个方向观察物体,投影到一个平面上。通常情况下,侧视图的观察方向是从侧面,也就是X轴正方向。投影平面一般是平行于Y-Z平面。
具体实现可以通过以下步骤完成:
- 定义观察点坐标和投影平面距离
- 对3D坐标进行透视变换
- 对透视变换后的坐标进行投影变换
- 将投影后的坐标映射到屏幕上
示例代码:
int x_2d = (int) (y_3d / (x_3d - view_point_x) * distance_to_projection_plane);
int y_2d = (int) (z_3d / (x_3d - view_point_x) * distance_to_projection_plane);
3. 俯视图投影
俯视图投影是指以一个点作为视点,从一个方向观察物体,投影到一个平面上。通常情况下,俯视图的观察方向是从上方,也就是Y轴正方向。投影平面一般是平行于X-Z平面。
具体实现可以通过以下步骤完成:
- 定义观察点坐标和投影平面距离
- 对3D坐标进行透视变换
- 对透视变换后的坐标进行投影变换
- 将投影后的坐标映射到屏幕上
以下是一个简单的示例代码,用于将3D空间中的点坐标转化为屏幕二维点坐标。这里包括了主视图、侧视图、俯视图、正等轴投影的实现。
#include <stdio.h>
#include <stdlib.h>
#include <math.h>#define SCREEN_WIDTH 640
#define SCREEN_HEIGHT 480typedef struct {double x, y, z;
} Point3D;typedef struct {int x, y;
} Point2D;void project_ortho(Point3D point_3d, Point2D *point_2d, double distance_to_projection_plane) {point_2d->x = (int) point_3d.x;point_2d->y = (int) point_3d.y;
}void project_isometric(Point3D point_3d, Point2D *point_2d, double distance_to_projection_plane) {point_2d->x = (int) ((point_3d.x - point_3d.z) * cos(30 * M_PI / 180));point_2d->y = (int) ((point_3d.y - (point_3d.x + point_3d.z) * sin(30 * M_PI / 180)) * cos(30 * M_PI / 180));
}void project_main(Point3D point_3d, Point2D *point_2d, Point3D view_point, double distance_to_projection_plane) {double z_3d = point_3d.z - view_point.z;point_2d->x = (int) (point_3d.x - view_point.x) * distance_to_projection_plane / z_3d + SCREEN_WIDTH / 2;point_2d->y = (int) (point_3d.y - view_point.y) * distance_to_projection_plane / z_3d + SCREEN_HEIGHT / 2;
}void project_side(Point3D point_3d, Point2D *point_2d, Point3D view_point, double distance_to_projection_plane) {double x_3d = point_3d.x - view_point.x;point_2d->x = (int) (point_3d.y - view_point.y) * distance_to_projection_plane / x_3d + SCREEN_WIDTH / 2;point_2d->y = (int) (point_3d.z - view_point.z) * distance_to_projection_plane / x_3d + SCREEN_HEIGHT / 2;
}void project_top(Point3D point_3d, Point2D *point_2d, Point3D view_point, double distance_to_projection_plane) {double y_3d = point_3d.y - view_point.y;point_2d->x = (int) (point_3d.x - view_point.x) * distance_to_projection_plane / y_3d + SCREEN_WIDTH / 2;point_2d->y = (int) (point_3d.z - view_point.z) * distance_to_projection_plane / y_3d + SCREEN_HEIGHT / 2;
}int main() {// Define the 3D points of a cubePoint3D cube[8] = {{-50, -50, -50},{50, -50, -50},{50, 50, -50},{-50, 50, -50},{50, -50, 50},{50, 50, 50},{-50, 50, 50},{-50, -50, 50},};// Define the view point for the main, side, and top projectionsPoint3D main_view_point = {0, 0, 200};Point3D side_view_point = {-200, 0, 0};Point3D top_view_point = {0, 200, 0};// Define the distance from the projection plane for the orthogonal and isometric projectionsdouble distance_to_ortho_projection_plane = 200;double distance_to_isometric_projection_plane = 200 / cos(30 * M_PI / 180);// Project the 3D points to 2D points for each projectionPoint2D main_projection[8];Point2D side_projection[8];Point2D top_projection[8];Point2D ortho_projection[8];Point2D iso_projection[8];int i;for (i = 0; i < 8; i++) {project_main(cube[i], &main_projection[i], main_view_point, distance_to_ortho_projection_plane);project_side(cube[i], &side_projection[i], side_view_point, distance_to_ortho_projection_plane);project_top(cube[i], &top_projection[i], top_view_point, distance_to_ortho_projection_plane);project_ortho(cube[i], &ortho_projection[i], distance_to_ortho_projection_plane);project_isometric(cube[i], &iso_projection[i], distance_to_isometric_projection_plane);}// Draw the 2D projections// ...// Your code to draw the projections goes here// ...return 0;
}
相关文章:

用纯C语言实现3D空间中的点坐标转化为屏幕二维点坐标,包含主视图、侧视图、俯视图、正等轴投影
要实现3D空间中的点坐标转换为屏幕二维点坐标,需要进行透视变换和投影变换。以下是一些基本的思路和示例代码,可以用于实现主视图、侧视图、俯视图、正等轴投影。 1. 主视图投影 主视图投影是指以一个点作为视点,从一个方向观察物体&#x…...

.sh脚本文件的执行方式
方法1: ./xxx.sh方法2: source xxx.sh方法3: bash xxx.sh方法4: sh xxx.sh初识shell,学习并记录...

Android 基础知识4-2.5View与VIewGroup的概念、关系与区别
1.概念: Android里的图形界面都是由View和ViewGroup以及他们的子类构成的: View:所有可视化控件的父类,提供组件描绘和时间处理方法 ViewGroup: View类的子类,可以拥有子控件,可以看作是容器 Android UI中的控件都是…...

【ESP 保姆级教程】玩转巴法云篇① ——初识巴法云
忘记过去,超越自己 ❤️ 博客主页 单片机菜鸟哥,一个野生非专业硬件IOT爱好者 ❤️❤️ 本篇创建记录 2023-02-19 ❤️❤️ 本篇更新记录 2023-02-19 ❤️🎉 欢迎关注 🔎点赞 👍收藏 ⭐️留言📝🙏 此博客均由博主单独编写,不存在任何商业团队运营,如发现错误,请…...

Python学习-----模块3.0(正则表达式-->re模块)
目录 前言: 导入模块 1.re.match() 函数 (1)匹配单个字符 (2)匹配多个字符 (3) 匹配开头和结尾 2.re.search() 函数 3.re.findall() 函数 4.re.finditer() 函数 5.re.split() 函数 6.re.sub() 函数 7.re.sub…...
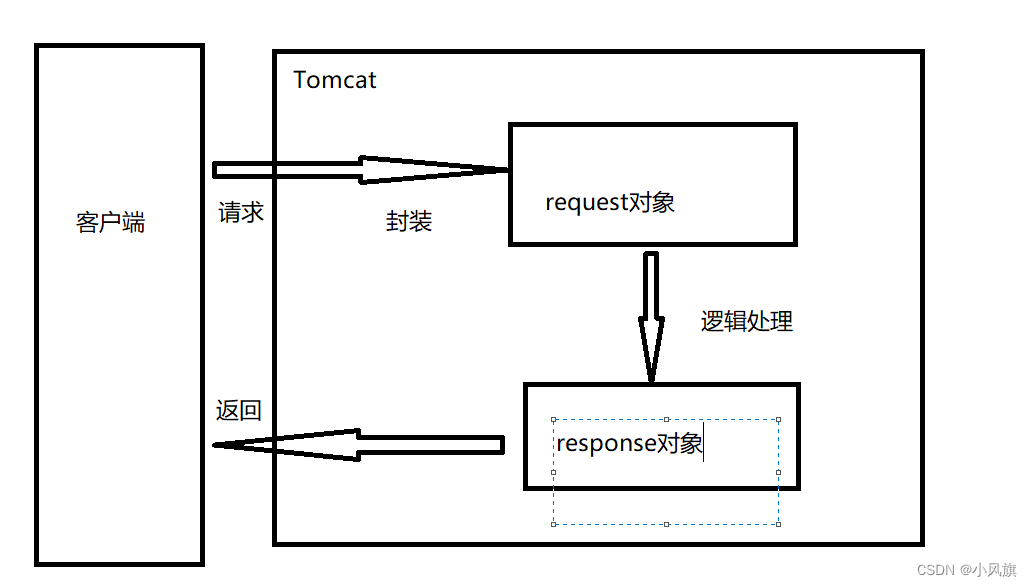
JSP中http与内置对象学习笔记
本博文讲述jsp客户端与服务器端的http、jsp内置对象与控制流和数据流实现 1.HTTP请求响应机制 HTTP协议是TCP/IP协议中的一个应用层协议,用于定义客户端与服务器之间交换数据的过程 1.1 HTTP请求 HTTP请求由请求行、消息报头、空行和请求数据4部分组成。 请求行…...
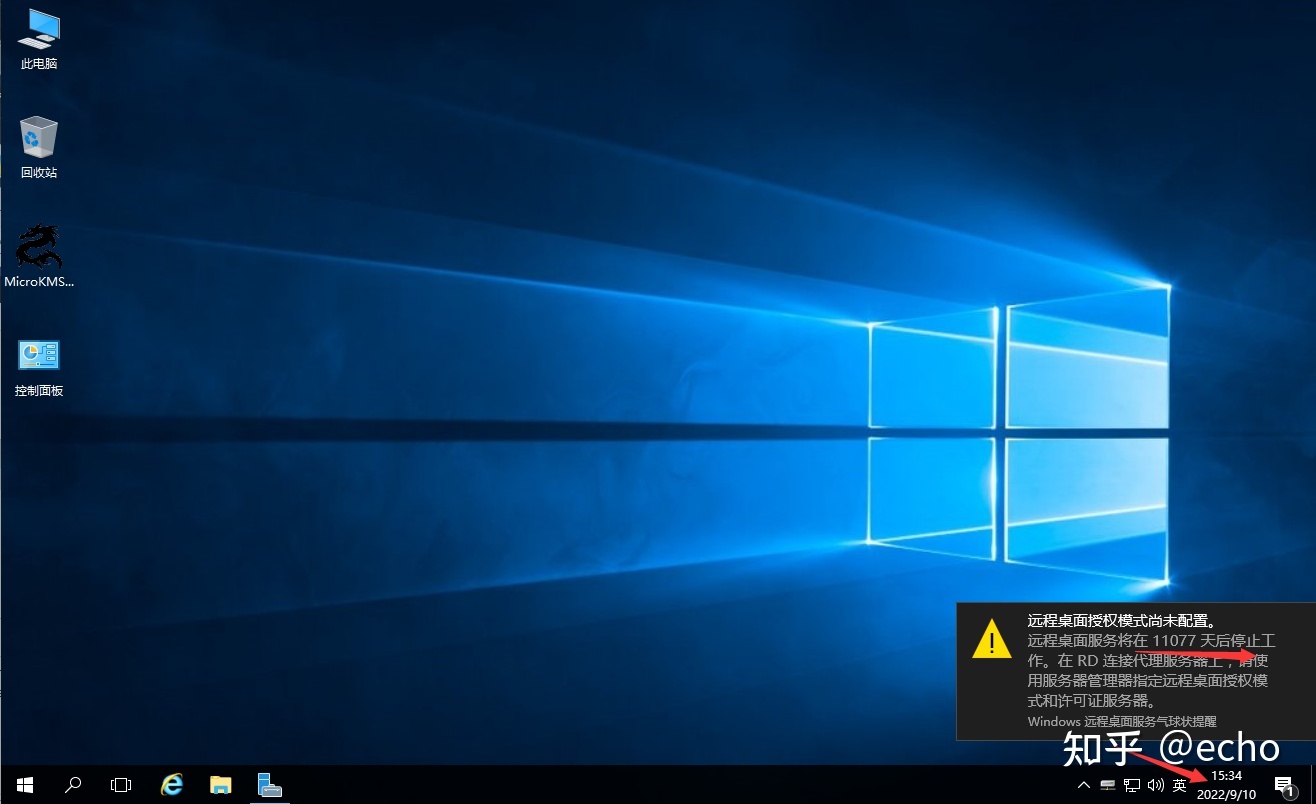
Windows Server 2016远程桌面配置全过程
镜像下载 系统镜像网址 本次下载的是 Windows Server 2016 (Updated Feb 2018) (x64) - DVD (Chinese-Simplified) 远程桌面配置 Step 1 在开始菜单搜索服务,打开服务器管理器,点击右上角的管理按钮 Step 2 添加角色控制,点击下一步 S…...
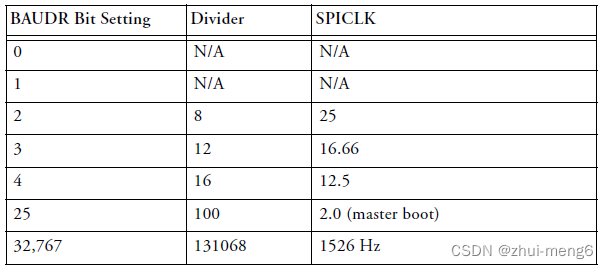
SPI通讯简介
一、基本概念 SPI是串行外设接口(Serial Peripheral Interface)的缩写,是一种高速的,全双工,同步的通信总线,主要应用在EEPROM,FLASH,实时时钟,AD转换器,多MCU间通讯等等,SPI端口可以在多主器件…...

Python 迭代器
迭代器协议 对象必须提供一个 next() 方法,执行该方法要么迭代下一项,要么就引起一个 StopIteration异常以终止迭代(只能往后不能往前)—— 迭代器协议 协议是一种约定,可迭代对象实现了迭代器协议(for、…...
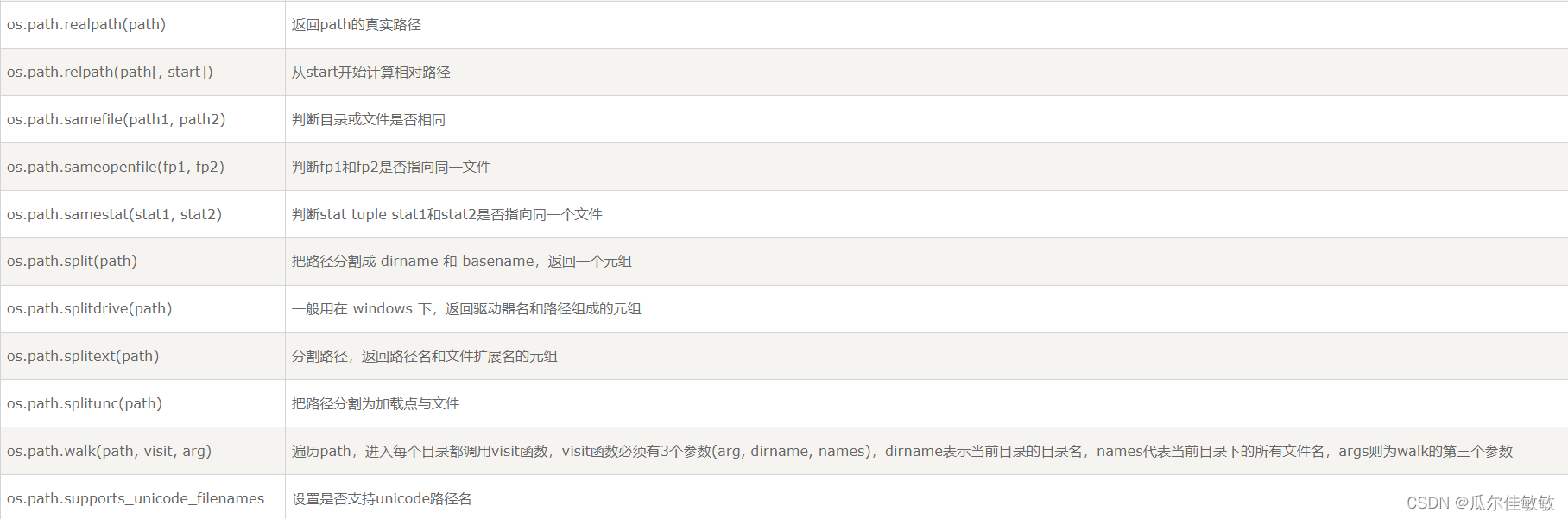
Python语言零基础入门教程(二十七)
Python OS 文件/目录方法 Python语言零基础入门教程(二十六) 61、Python os.utime() 方法 概述 os.utime() 方法用于设置指定路径文件最后的修改和访问时间。 在Unix,Windows中有效。 语法 utime()方法语法格式如下: os.uti…...

Redis基础操作以及数据类型
目录 Redis基础操作 java中的i是不是原子操作?不是 数据类型 1. list 2. set 3. Hash哈希 4. Zset有序集合 Redis基础操作 set [key] [value] 设置值 (设置相同的会将原先的覆盖) get [key] 获取值 不能覆盖和替换 ttl [key] 以秒为单…...
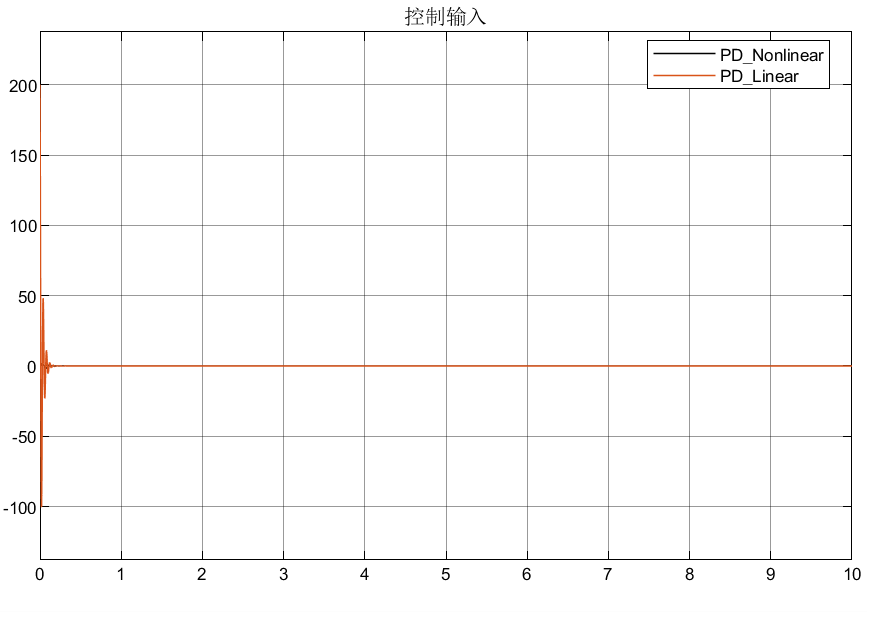
自抗扰控制ADRC之反馈控制律(NLSEF)
目录 前言 1.非线性状态误差反馈控制律(NLSEF) 1.1 控制律形式 1.2 控制量的生成(或者说扰动的补偿) 1.2.1补偿形式① 1.2.1补偿形式② 2.仿真分析 2.1仿真模型 2.2仿真结果 前言 前面的两篇博客依次介绍了TD微分跟踪器安排过渡过程、扩张观测器: 自抗扰…...
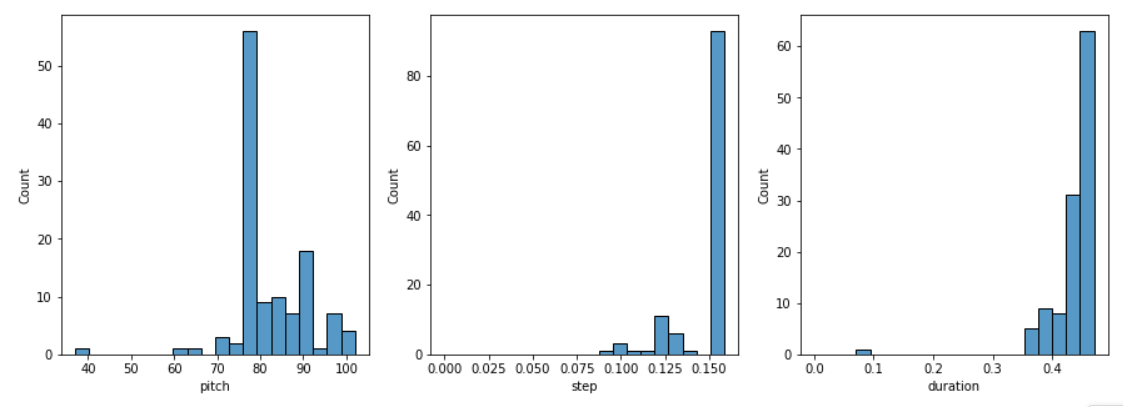
“生成音乐“ 【循环神经网络】
前言 本文介绍循环神经网络的进阶案例,通过搭建和训练一个模型,来对钢琴的音符进行预测,通过重复调用模型来进而生成一段音乐; 使用到Maestro的钢琴MIDI文件 ,每个文件由不同音符组成,音符用三个量来表示…...

能否手写vue3响应式原理-面试进阶
(二)响应式原理 利用ES6中Proxy作为拦截器,在get时收集依赖,在set时触发依赖,来实现响应式。 (三)手写实现 1、实现Reactive 基于原理,我们可以先写一下测试用例 //reactive.spe…...
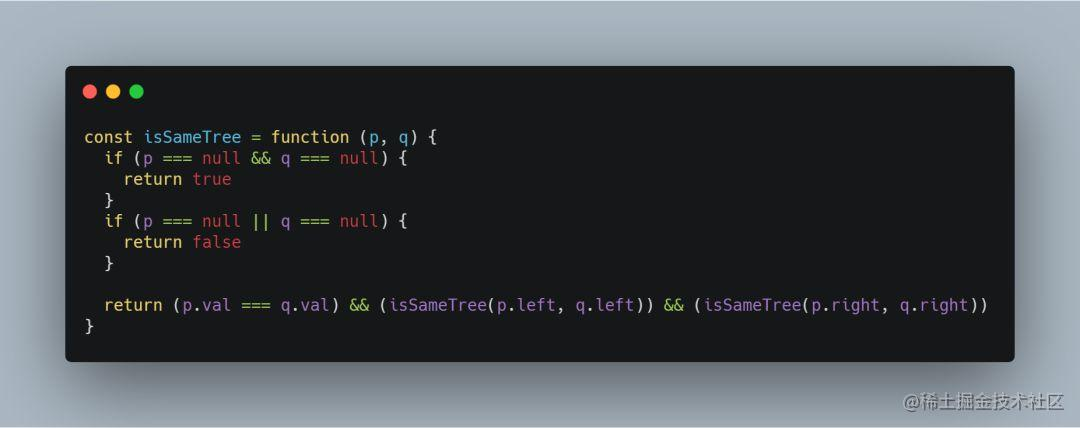
前端工程师leetcode算法面试必备-简单的二叉树
一、前言 本难度的题目主要考察二叉树的基本概念和操作。 1、基本概念 树是计算机科学中经常用到的一种非线性数据结构,以分层的形式存储数据。二叉树是一种特殊的树结构,每个节点最多有两个子树,通常子树被称作“左子树”和“右子树”。 …...

【什么程度叫熟悉linux系统】
一、编译内核 1、Linux系统背景:Ubuntu 2、内核源码kernel.org进行下载 3、解压内核源文件linux-6.1.12.tar.xz、命令:tar -xvf linux-6.1.12.tar.xz 4、进入解压好的文件inux-6.1.12 5、配置内核命令:make menuconfig(需要进…...

编译安装MySQL
MySQL 5.7主要特性 随机root 密码:MySQL 5.7 数据库初始化完成后,会自动生成一个 rootlocalhost 用户,root 用户的密码不为空,而是随机产生一个密码。原生支持:Systemd 更好的性能:对于多核CPU、固态硬盘、…...
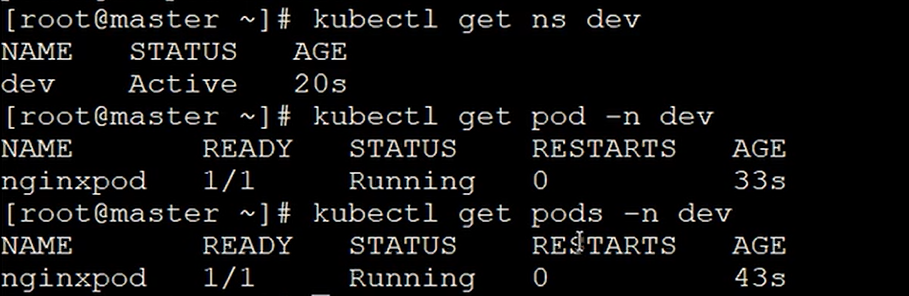
Kubernetes一 Kubernetes之入门
二 Kubernetes介绍 1.1 应用部署方式演变 在部署应用程序的方式上,主要经历了三个时代: 传统部署:互联网早期,会直接将应用程序部署在物理机上 优点:简单,不需要其它技术的参与 缺点:不能为应…...

SQLServer2000 断电后数据库suspect“置疑”处理
SQLServer2000 断电后数据库suspect“置疑”处理 背景介绍: 前些天加班时候,接到小舅子微信,说一个客户的winXP 机器上sql2000的数据库在断电重启后,数据库执行命令时提示suspect“置疑”错误。小舅子电子工程师,对数…...

多模态机器学习入门Tutorial on MultiModal Machine Learning——第一堂课个人学习内容
文章目录课程记录核心技术Core Technical Challengesrepresentation表示alignment对齐转换translationFusion融合co-learning共同学习总结Course Syllabus教学大纲个人总结第一周的安排相关连接课程记录 这部分是自己看视频,然后截屏,记录下来的这部分的…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...

Netty自定义协议解析
目录 自定义协议设计 实现消息解码器 实现消息编码器 自定义消息对象 配置ChannelPipeline Netty提供了强大的编解码器抽象基类,这些基类能够帮助开发者快速实现自定义协议的解析。 自定义协议设计 在实现自定义协议解析之前,需要明确协议的具体格式。例如,一个简单的…...
