【Diffusion】李宏毅2023机器学习Diffusion笔记
文章目录
- 1 想法概述
- 2 实际过程
- 阶段1 Add Noise
- 阶段2 Denoise
- 3 数学原理
- 4 为什么推理时要额外加入noise
- 5 一些不知道对不对的Summary
1 想法概述
从一张充满噪声的图中不断denoise,最终得到一张clear的图片。为了确定当前图片中噪声占比的大小,同时输入原图片和参数 t t t,参数 t t t用于标识一张图片中的噪声占比含量。
显然迭代第1次时图片的噪声含量和迭代第999次是不同的,因此需要输入这种信息t来进行标识。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7CjpzYoX-1692290104065)(【Diffusion】李宏毅2023机器学习Diffusion笔记/image-20230814190229199.png)]](https://img-blog.csdnimg.cn/4f4e17d3e69340118b4f01c429735850.png)
2 实际过程
阶段1 Add Noise
首先,准备好一组确定的参数 α 1 ˉ , α 2 ˉ , … , α T ˉ \bar{\alpha_1},\bar{\alpha_2},\dots,\bar{\alpha_T} α1ˉ,α2ˉ,…,αTˉ,用以表示时间步 t t t下样本和噪声的混合情况, t t t越大,噪声占比越高。然后重复以下过程直至收敛:
-
采样
-
从真实样本集中取出一个样本 x 0 x_0 x0
-
从 [ 1 , T ] [1,T] [1,T]的整数中采样出 t t t来表示时间步
-
从标准正态分布中采样出噪声 ϵ \epsilon ϵ
-
-
构造带噪声样本 x = α t ˉ x 0 + 1 − α t ˉ ϵ x=\sqrt{\bar{\alpha_t}}x_0+ \sqrt{1-\bar{\alpha_t}} \epsilon x=αtˉx0+1−αtˉϵ
-
将构造样本 x x x和时间步 t t t一同输入噪声预测器 ϵ θ ( ) \epsilon_\theta() ϵθ(),得到预测噪声 ϵ θ ( x , t ) \epsilon_\theta(x,t) ϵθ(x,t)。
-
目标函数为 ϵ θ ( x , t ) \epsilon_\theta(x,t) ϵθ(x,t)和采样出的真实噪声 ϵ \epsilon ϵ的 M S E MSE MSE
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-D7mqKw6q-1692290104066)(【Diffusion】李宏毅2023机器学习Diffusion笔记/image-20230814194524251.png)]](https://img-blog.csdnimg.cn/c04335120773405a8bdf66cd3009269b.png)
阶段2 Denoise
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-21zUXHgj-1692290104066)(【Diffusion】李宏毅2023机器学习Diffusion笔记/image-20230814201251917.png)]](https://img-blog.csdnimg.cn/31eb1bfa22734d9ba5246a0c317d3e00.png)
3 数学原理
- 极大似然估计近似等价于最小化KL散度(表示两个分布的相似性):
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-S3lKC0VE-1692290104066)(【Diffusion】李宏毅2023机器学习Diffusion笔记/image-20230817221857642.png)]](https://img-blog.csdnimg.cn/f71fb4de1faa4b4080fbadc62dba0b0a.png)
- 对任何分布 q ( z ∣ x ) q(z|x) q(z∣x),有:
log P θ ( x ) ≥ ∫ z q ( z ∣ x ) log P ( z , x ) q ( z ∣ x ) d z = E q ( z ∣ x ) [ log P ( z , x ) q ( z ∣ x ) ] \log P_\theta(x) \ge \int_{z}q(z|x)\log \frac{P(z,x)}{q(z|x)}dz = E_{q(z|x)}[\log \frac{P(z,x)}{q(z|x)}] logPθ(x)≥∫zq(z∣x)logq(z∣x)P(z,x)dz=Eq(z∣x)[logq(z∣x)P(z,x)]
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EMBIDtfT-1692290104067)(【Diffusion】李宏毅2023机器学习Diffusion笔记/image-20230817222057765.png)]](https://img-blog.csdnimg.cn/2383ae51d3b14fff84fbed64cb5fdd62.png)
- 所以对DDPM来说:
log P θ ( x ) ≥ E q ( x 1 : x T ∣ x 0 ) [ log P ( x 0 : x T ) q ( x 1 : x T ∣ x 0 ) ] \log P_\theta(x) \ge E_{q(x_1:x_T|x_0)}[\log \frac{P(x_0:x_T)}{q(x_1:x_T|x_0)}] logPθ(x)≥Eq(x1:xT∣x0)[logq(x1:xT∣x0)P(x0:xT)]
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FqgMWPQQ-1692290104067)(【Diffusion】李宏毅2023机器学习Diffusion笔记/image-20230817222642961.png)]](https://img-blog.csdnimg.cn/d91ef7dc43b54294850f028358d3f1a3.png)
- 结合正态分布的可加性:做N次独立的正态sampling,可能通过一次的sampling就能解决。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oyzChf3t-1692290104067)(【Diffusion】李宏毅2023机器学习Diffusion笔记/image-20230817225900399.png)]](https://img-blog.csdnimg.cn/767e444ef5204f839cc0b930f56e1349.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-w4gtTsG6-1692290104067)(【Diffusion】李宏毅2023机器学习Diffusion笔记/image-20230817231727538.png)]](https://img-blog.csdnimg.cn/bf47251d15fa41589595d129dc70d2a8.png)
- 对式3不断变换,最后可得(这个式子的过程可以不用看,也并不复杂,但是麻烦,理解结论就好):
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SY9fKeIh-1692290104068)(【Diffusion】李宏毅2023机器学习Diffusion笔记/image-20230817232929967.png)]](https://img-blog.csdnimg.cn/f4cea90358114568a48d9426017d81b9.png)
然后再经过一系列的运算求出来 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1|x_t,x_0}) q(xt−1∣xt,x0)依然是高斯分布,表示首尾 x 0 , x T x_0,x_T x0,xT固定住,产生 x t − 1 x_{t-1} xt−1的概率,是一个和network无关的分布。而 P ( x t − 1 ∣ x t ) P(x_{t-1}|x_t) P(xt−1∣xt)是由网络决定的,我们不考虑它的variance,只考虑mean。如果我们希望这两个分布越接近越好,那就想办法让两个分布的mean越接近越好。
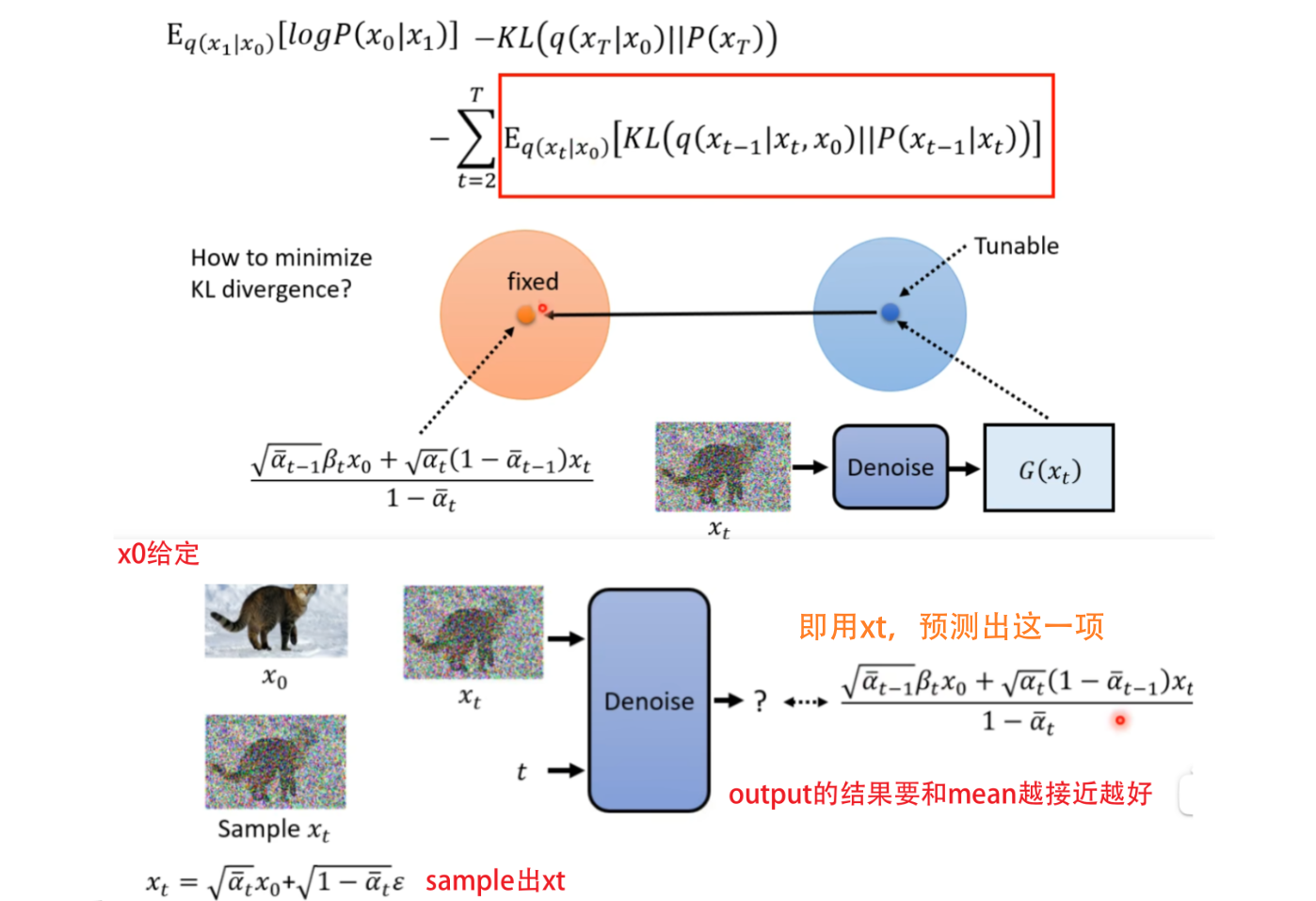
化简:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-B0OFKfc5-1692290104068)(【Diffusion】李宏毅2023机器学习Diffusion笔记/image-20230817233152037.png)]](https://img-blog.csdnimg.cn/94875687bc15457f8d78d4a50400a5d5.png)
实际需要预测出的部分:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OpE6Y02O-1692290104069)(【Diffusion】李宏毅2023机器学习Diffusion笔记/image-20230817234731710.png)]](https://img-blog.csdnimg.cn/058ce2f63eaa42ef97aa502ab8d92950.png)
4 为什么推理时要额外加入noise
李宏毅老师的一点Guess,生成式任务,概率最大的结果,未必就是最好的结果。人写的文章用词可能更suprising。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BxAIdBaQ-1692290104069)(【Diffusion】李宏毅2023机器学习Diffusion笔记/image-20230817235534101.png)]](https://img-blog.csdnimg.cn/2b08a21cf6bb432e806ba75c8e148d30.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-w8wYcaVO-1692290104069)(【Diffusion】李宏毅2023机器学习Diffusion笔记/image-20230817235706919.png)]](https://img-blog.csdnimg.cn/ced2475cfe794eeca024204e5f32ceaf.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vmK39t6D-1692290104069)(【Diffusion】李宏毅2023机器学习Diffusion笔记/ab7e3c6482dc90f4bfc5857991f4375.jpg)]](https://img-blog.csdnimg.cn/41fca1f566d14926833764da62bd92ec.png)
5 一些不知道对不对的Summary
-
希望近似 P d a t a ( x ) P_{data}(x) Pdata(x)和 P θ ( x ) P_\theta(x) Pθ(x)的分布,而对给定的 x x x,使 P θ ( x ) P_\theta(x) Pθ(x)最大化可以转换为使其下界最大化,从而转换为使 E q ( x 1 : x T ∣ x 0 ) [ log P ( x 0 : x T ) q ( x 1 : x T ∣ x 0 ) ] E_{q(x_1:x_T|x_0)}[\log \frac{P(x_0:x_T)}{q(x_1:x_T|x_0)}] Eq(x1:xT∣x0)[logq(x1:xT∣x0)P(x0:xT)]最大化。
-
在假设 x t = β t x t − 1 + 1 − β t z t − 1 x_t=\sqrt{\beta_t}x_{t-1}+\sqrt{1-\beta_t}z_{t-1} xt=βtxt−1+1−βtzt−1的前提下,可以推出 x t = α t ˉ x 0 + 1 − α t ˉ z x_t=\sqrt{\bar{\alpha_t}}x_{0}+\sqrt{1-\bar{\alpha_t}}z xt=αtˉx0+1−αtˉz
-
从而可以进一步化简 E q ( x 1 : x T ∣ x 0 ) [ log P ( x 0 : x T ) q ( x 1 : x T ∣ x 0 ) ] E_{q(x_1:x_T|x_0)}[\log \frac{P(x_0:x_T)}{q(x_1:x_T|x_0)}] Eq(x1:xT∣x0)[logq(x1:xT∣x0)P(x0:xT)]为三项,其余两项与Network无关,可只考虑中间一项,该项由 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1|x_t,x_0}) q(xt−1∣xt,x0)和 P ( x t − 1 ∣ x t ) P(x_{t-1}|x_t) P(xt−1∣xt)的KL散度之和组成,
-
q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)表示首尾 x 0 , x T x_0,x_T x0,xT固定住产生 x t − 1 x_{t-1} xt−1的概率,可求得是一个和network无关的高斯分布,均值可以表示为:
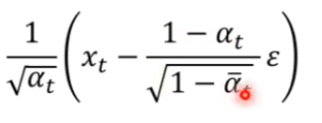
-
而 P ( x t − 1 ∣ x t ) P(x_{t-1}|x_t) P(xt−1∣xt)是由网络决定的,我们不考虑它的variance,只考虑mean。
-
如果我们希望这两个分布越接近越好,那就想办法让两个分布的mean越接近越好。而上式中,仅有 ϵ \epsilon ϵ需要确定,因此我们希望网络能够预测这个值,从而完成推理。预测出这一项 ϵ \epsilon ϵ的过程,可以看作为从 x 0 x_0 x0和 x t x_t xt预测出 x t − 1 x_{t-1} xt−1的过程。
相关文章:
【Diffusion】李宏毅2023机器学习Diffusion笔记
文章目录 1 想法概述2 实际过程阶段1 Add Noise阶段2 Denoise 3 数学原理4 为什么推理时要额外加入noise5 一些不知道对不对的Summary 1 想法概述 从一张充满噪声的图中不断denoise,最终得到一张clear的图片。为了确定当前图片中噪声占比的大小,同时输入…...

CloudEvents—云原生事件规范
我们的系统中或多或少都会用到如下两类业务技术: 异步任务,用于降低接口时延或削峰,提升用户体验,降低系统并发压力;通知类RPC,用于微服务间状态变更,用户行为的联动等场景; 以上两种…...

神经网络基础-神经网络补充概念-51-局部最优问题
概念 局部最优问题是在优化问题中常见的一个挑战,特别是在高维、非凸、非线性问题中。局部最优问题指的是算法在优化过程中陷入了一个局部最小值点,而不是全局最小值点。这会导致优化算法在某个局部区域停止,而无法找到更好的解。 解决方案…...

深度学习中,什么是batch-size?如何设置?
什么是batch-size? batch-size 是深度学习模型在训练过程中一次性输入给模型的样本数量。它在训练过程中具有重要的意义,影响着训练速度、内存使用以及模型的稳定性等方面。 以下是 batch-size 大小的一些影响和意义: 训练速度:较大的 bat…...
[保研/考研机试] KY26 10进制 VS 2进制 清华大学复试上机题 C++实现
题目链接: 10进制 VS 2进制http://www.nowcoder.com/share/jump/437195121691738172415 描述 对于一个十进制数A,将A转换为二进制数,然后按位逆序排列,再转换为十进制数B,我们称B为A的二进制逆序数。 例如对于十进制…...
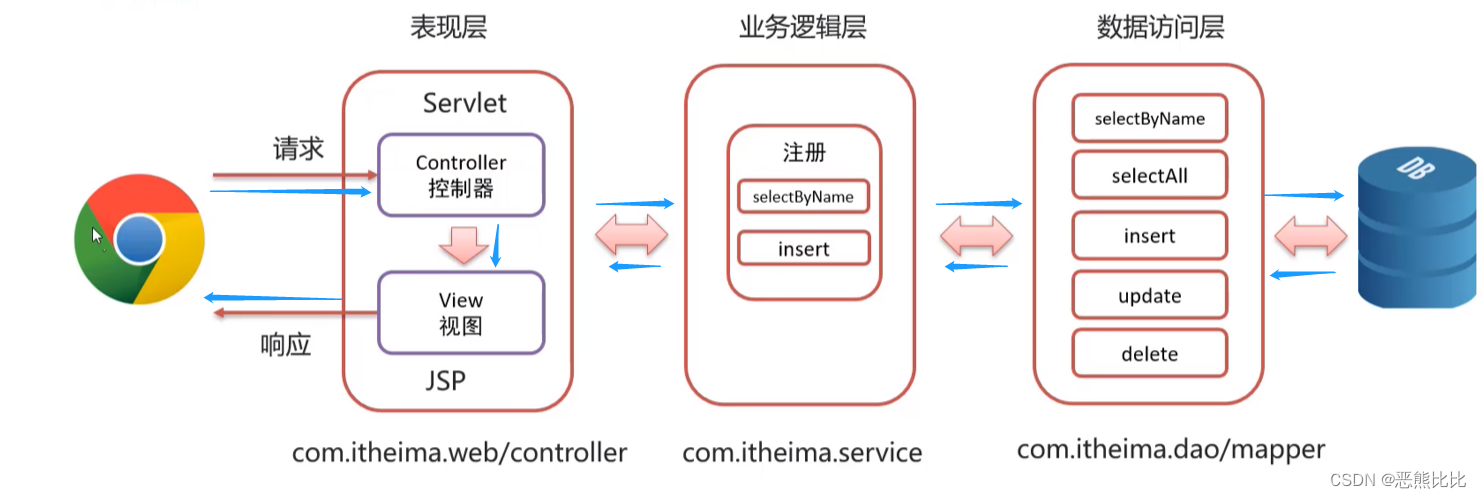
JSP-学习笔记
文章目录 1.JSP介绍2 JSP快速入门3 JSP 脚本3.1 JSP脚本案例3.2 JSP缺点 4 EL表达式4.1 快速入门案例 5. JSTL标签6. MVC模式和三层架构6.1 MVC6.2 三层架构 7. 案例-基于MVC和三层架构实现商品表的增删改查 1.JSP介绍 概念 JSP(JavaServer Pages)是一种…...
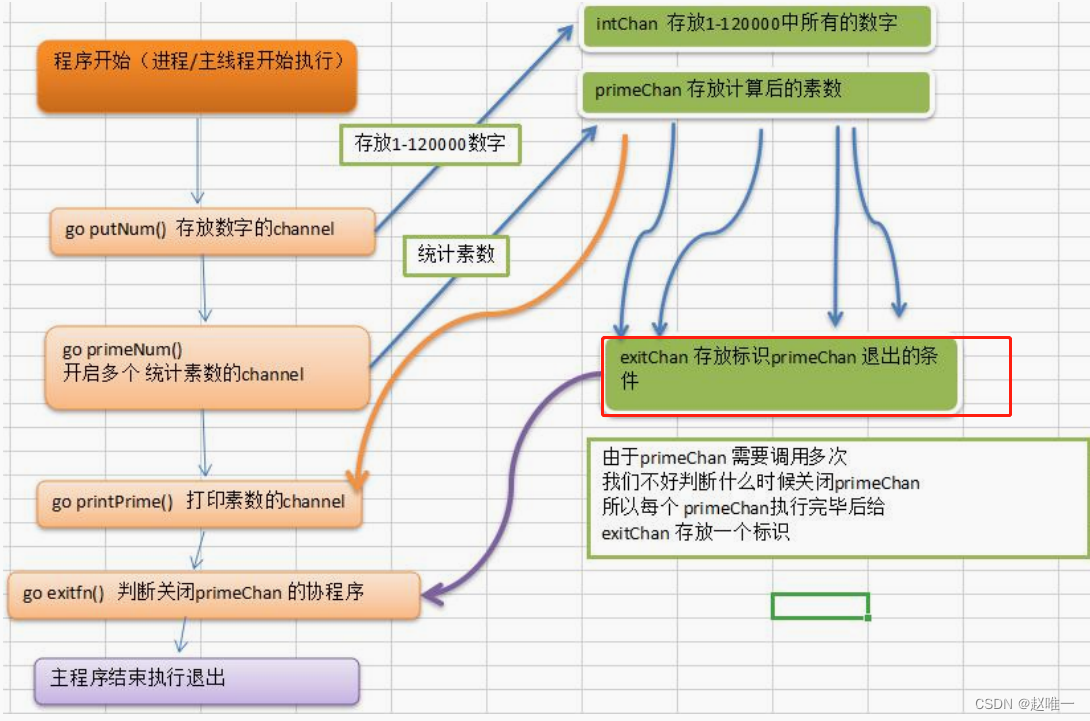
Golang协程,通道详解
进程、线程以及并行、并发 关于进程和线程 进程(Process)就是程序在操作系统中的一次执行过程,是系统进行资源分配和调度的基本单位,进程是一个动态概念,是程序在执行过程中分配和管理资源的基本单位,每一…...

unity 之 Vector 数据类型
文章目录 Vector 1Vector 2Vector 3Vector 4 Vector 1 在Unity中,Vector1 并不是一个常见的向量类型。 如果您需要表示标量(单个值)或者只需要一维的数据,通常会直接使用浮点数(float)或整数(in…...

私密数据采集:隧道爬虫IP技术的保密性能力探究
作为一名专业的爬虫程序员,今天要和大家分享一个关键的技术,它能够为私密数据采集提供保密性能力——隧道爬虫IP技术。如果你在进行敏感数据采集任务时需要保护数据的私密性,那么这项技术将是你的守护神。 在进行私密数据采集任务时ÿ…...

使用git rebase 之后的如何恢复到原始状态
我们常常喜欢使用git rebase去切换分支提交代码,操作流程就是: 先切换分支:比如当前是master 我们修改了一堆代码产生一个commit id :5555555567777 那么我们常常比较懒就直接切换了:git checkout dev 然后呢?使用命令git rebase 5555555567777,想把这笔修改提交到d…...

matlab相机标定知识整理
matlab相机标定知识整理 单目相机标定 单目相机标定 内参矩阵:cameraParams.Intrinsics.K 或者 cameraParams.K旋转矩阵:cameraParams.RotationMatrices 有待确定 cameraParams.RotationVectors平移矩阵:cameraParams.TranslationVectors径向…...

win11安装ubuntu 子系统安装过程及注意事项
第一步 :安装系统必须组件 由于子系统是系统自带组件,需要安装软件支持 第二步:应用商店安装 ubuntu 编辑 编辑 这个时候打开会报错 第三步,运行linux子系统 选择Windows PowerShell 以管理员身份运行) 输入&#…...
,dim=1)解析)
torch.cat((A,B),dim=1)解析
官方说明torch.cat 引用自:Pytorch中的torch.cat()函数 torch.cat(tensors, dim0, *, outNone) → Tensor # 连接给定维数的给定序列的序列张量。所有张量要么具有相同的形状(除了连接维度),要么为空。示例 输入: import torch a torch.Tens…...

apache配置安全证书https踩坑记录
apache配置安全证书有如下几步 一、申请证书 这个网上有很多免费的,我用的是阿里云的服务器,在阿里云后台就可以申请免费证书。 二、上传证书 申请好证书后,根据服务器用的什么软件,是apache还是ngnix,下载相应的证书…...
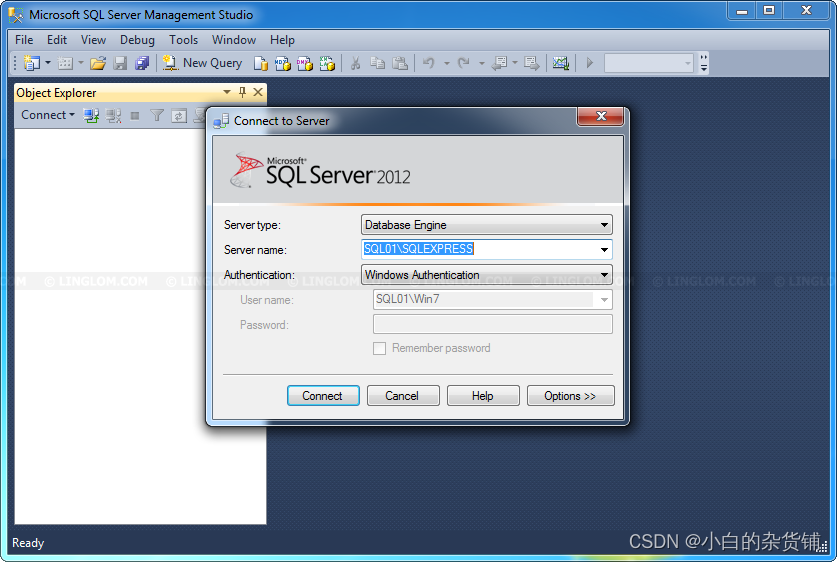
SQL Server Express 自动备份方案
文章目录 SQL Server Express 自动备份方案前言方案原理SQL Server Express 自动备份1.创建存储过程2.设定计划任务3.结果检查sqlcmd 参数说明SQL Server Express 自动备份方案 前言 对于许多小型企业和个人开发者来说,SQL Server Express是一个经济实惠且强大的数据库解决方…...

Docker资源控制
目录 一、CPU 资源控制 1.设置CPU使用率上限 2.设置CPU资源占用比(设置多个容器时才有效) 3.设置容器绑定指定的CPU 二、对内存使用的限制 三、对磁盘IO配额控制(blkio)的限制 一、CPU 资源控制 cgroups,是一个非常强…...
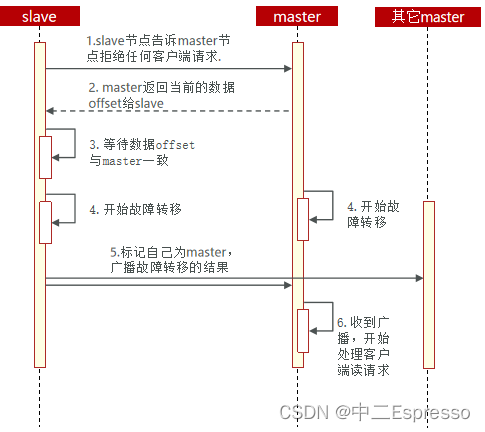
微服务中间件-分布式缓存Redis
分布式缓存 a.Redis持久化1) RDB持久化1.a) RDB持久化-原理 2) AOF持久化3) 两者对比 b.Redis主从1) 搭建主从架构2) 数据同步原理(全量同步)3) 数据同步原理(增量同步) c.Redis哨兵1) 哨兵的作用2) 搭建Redis哨兵集群3) RedisTem…...

java面试强基(16)
目录 clone方法的保护机制 Java中由SubString方法是否会引起内存泄漏? Java中提供了哪两种用于多态的机制? 程序计数器(线程私有) 如何判断对象是否是垃圾? clone方法的保护机制 clone0方法的保护机制在Object中是被声明为 protected的。以User…...
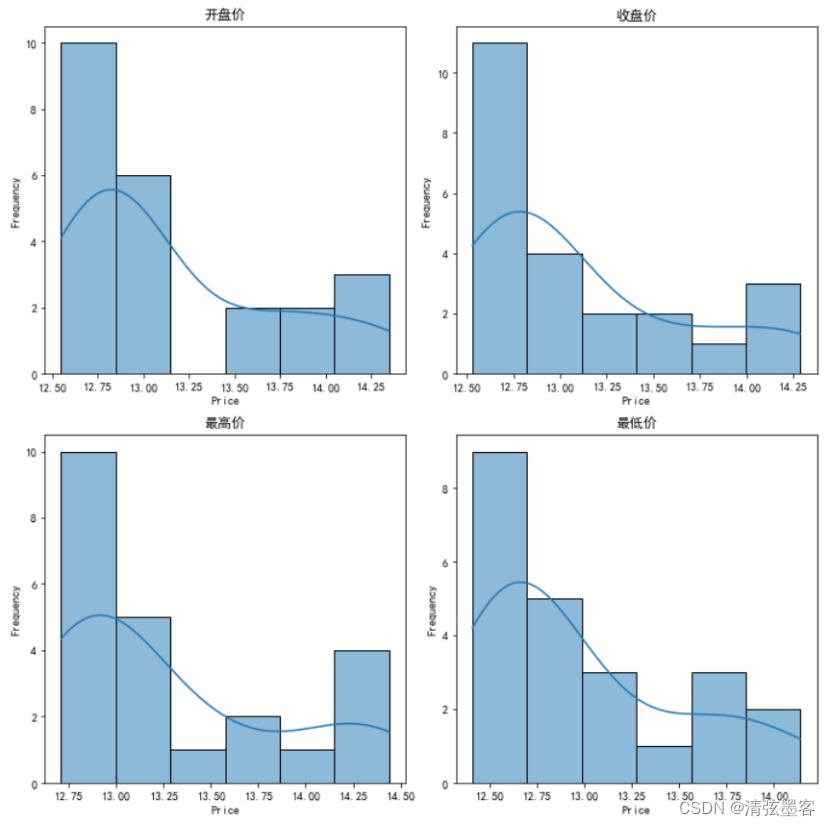
Python可视化在量化交易中的应用(13)_Seaborn直方图
Seaborn中带核密度的直方图的绘制方法 seaborn中绘制直方图使用的是sns.histlot()函数: sns.histplot(data,x,y,hue,weights,stat‘count’,bins‘auto’,binwidth,binrange,discrete,cumulative,common_bins,common_norm,multiple‘layer’,element‘bars’,fill,…...

NOIP 2006 普及组 第二题 开心的金明
开心的金明 说明 金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。 更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
