Greiner–Hormann裁剪算法深度探索:C++实现与应用案例
介绍
在计算几何中,裁剪是一个核心的主题。特别是,多边形裁剪已经被广泛地应用于计算机图形学,地理信息系统和许多其他领域。Greiner-Hormann裁剪算法是其中之一,提供了一个高效的方式来计算两个多边形的交集、并集等。在本文中,我们将深入探讨这一算法,并为您提供一个基于C++的实现。
算法概述
Greiner-Hormann算法基于边界交点的概念,即两个多边形的交点。算法的关键思想是找到这些交点,并根据需要合并多边形的顶点。
- 找到所有的交点:遍历多边形A和B的所有边,找到它们的交点。
- 排序交点:按照它们在多边形边上的位置对交点进行排序。
- 连接交点:使用链接交点来形成新的多边形。
- 得到结果多边形:得到交集、并集或差集,取决于所需的操作。
C++实现
为了简单起见,我们假设点是一个简单的结构,并有一个函数来计算两条线段的交点。
struct Point {double x, y;Point(double x = 0, double y = 0) : x(x), y(y) {}
};bool findIntersection(Point p1, Point q1, Point p2, Point q2, Point &intersec) {// ... (交点的计算代码)
}
为了表示多边形,我们使用点的列表:
using Polygon = std::vector<Point>;
现在,让我们开始寻找两个多边形之间的所有交点。
std::vector<Point> findIntersections(const Polygon &polyA, const Polygon &polyB) {std::vector<Point> intersections;for(size_t i = 0; i < polyA.size(); i++) {Point p1 = polyA[i];Point q1 = (i == polyA.size() - 1) ? polyA[0] : polyA[i + 1];for(size_t j = 0; j < polyB.size(); j++) {Point p2 = polyB[j];Point q2 = (j == polyB.size() - 1) ? polyB[0] : polyB[j + 1];Point intersec;if(findIntersection(p1, q1, p2, q2, intersec)) {intersections.push_back(intersec);}}}return intersections;
}
此代码片段首先初始化一个空的交点列表。然后,它遍历polyA和polyB的每条边,使用findIntersection函数来确定它们是否有交点。如果找到交点,它会添加到交点列表中。
排序交点
为了确保算法的正确性,我们需要按照它们在多边形上的位置对交点进行排序。这确保了当我们形成新的多边形时,交点被正确地处理。
void sortIntersections(Polygon &poly, std::vector<Point> &intersections) {std::sort(intersections.begin(), intersections.end(), [&poly](const Point &a, const Point &b) -> bool {// 为每个交点找到其在多边形上的位置size_t posA = std::distance(poly.begin(), std::find(poly.begin(), poly.end(), a));size_t posB = std::distance(poly.begin(), std::find(poly.begin(), poly.end(), b));return posA < posB;});
}
此函数接受多边形和其交点列表作为参数,然后按照交点在多边形上的位置进行排序。
连接交点以形成新的多边形
一旦我们有了排序后的交点,我们就可以开始构造新的多边形。
Polygon constructNewPolygon(const Polygon &polyA, const Polygon &polyB, const std::vector<Point> &intersections) {Polygon result;// 使用一个标记数组来跟踪哪些交点已经被处理std::vector<bool> visited(intersections.size(), false);// 开始于多边形A的第一个点result.push_back(polyA[0]);for (size_t i = 1; i <= polyA.size(); i++) {Point current = (i == polyA.size()) ? polyA[0] : polyA[i];// 查找是否有交点auto it = std::find(intersections.begin(), intersections.end(), current);if (it != intersections.end() && !visited[std::distance(intersections.begin(), it)]) {// 标记交点为已访问visited[std::distance(intersections.begin(), it)] = true;// 将交点添加到结果多边形中result.push_back(*it);// 转到另一个多边形并遍历其边,直到遇到另一个交点const Polygon &otherPoly = (polyA == polyB) ? polyB : polyA;size_t j = std::distance(otherPoly.begin(), std::find(otherPoly.begin(), otherPoly.end(), *it));do {j = (j + 1) % otherPoly.size();result.push_back(otherPoly[j]);} while (std::find(intersections.begin(), intersections.end(), otherPoly[j]) == intersections.end());} else {result.push_back(current);}}return result;
}
这个函数首先初始化了一个空的多边形和一个标记数组,用于跟踪哪些交点已经被处理。然后,它遍历polyA的每个顶点,并检查它是否是一个交点。如果是,并且还没有被访问过,它将开始遍历polyB,直到找到另一个交点为止。
结论和进一步的应用
从上面的C++实现中,我们可以看到Greiner-Hormann裁剪算法是如何工作的。这种算法的优点是它对于复杂的多边形也能高效工作,而且它的理论基础使得它可以很容易地适应各种应用场景。
例如,此算法不仅限于2D平面上的裁剪。通过在三维空间中考虑多边形,或者在N维空间中进行一些扩展,我们可以将此方法用于更高维度的空间。
此外,这种算法在图形渲染、地理信息系统、碰撞检测等领域都有应用。其准确性和效率使它成为处理这些问题的理想选择。
总结
Greiner-Hormann裁剪算法为我们提供了一个强大的工具,可以用来解决多边形裁剪中的各种问题。不仅如此,由于其底层原理和结构的普遍性,它可以被扩展到多种不同的应用中。上面提供的C++实现只是开始,您可以根据需要对其进行扩展或修改,使其适应您的特定需求。
感谢您的耐心阅读!希望这篇文章为您提供了有价值的信息和启示。
相关文章:

Greiner–Hormann裁剪算法深度探索:C++实现与应用案例
介绍 在计算几何中,裁剪是一个核心的主题。特别是,多边形裁剪已经被广泛地应用于计算机图形学,地理信息系统和许多其他领域。Greiner-Hormann裁剪算法是其中之一,提供了一个高效的方式来计算两个多边形的交集、并集等。在本文中&…...

Automatically Correcting Large Language Models
本文是大模型相关领域的系列文章,针对《Automatically Correcting Large Language Models: Surveying the landscape of diverse self-correction strategies》的翻译。 自动更正大型语言模型:综述各种自我更正策略的前景 摘要1 引言2 自动反馈校正LLM的…...
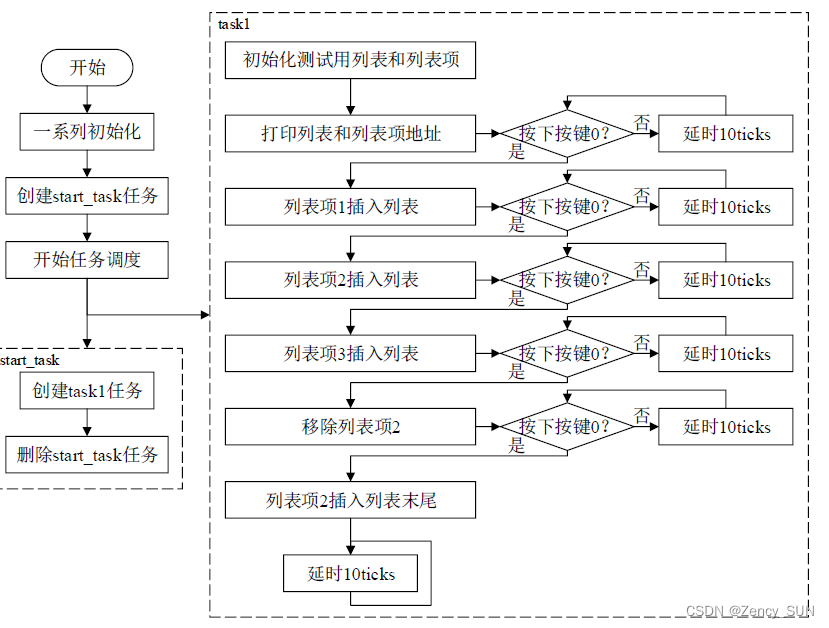
【学习FreeRTOS】第8章——FreeRTOS列表和列表项
1.列表和列表项的简介 列表是 FreeRTOS 中的一个数据结构,概念上和链表有点类似,列表被用来跟踪 FreeRTOS中的任务。列表项就是存放在列表中的项目。 列表相当于链表,列表项相当于节点,FreeRTOS 中的列表是一个双向环形链表列表的…...

分布式图数据库 NebulaGraph v3.6.0 正式发布,强化全文索引能力
本次 v3.6.0 版本,主要强化全文索引能力,以及优化部分场景下的 MATCH 性能。 强化 强化增强全文索引功能,具体 pr 参见:#5567、#5575、#5577、#5580、#5584、#5587 优化 支持使用 MATCH 子句检索 VID 或属性索引时使用变量&am…...
在 ubuntu 18.04 上使用源码升级 OpenSSH_7.6p1到 OpenSSH_9.3p1
1、检查系统已安装的当前 SSH 版本 使用命令 ssh -V 查看当前 ssh 版本,输出如下: OpenSSH_7.6p1 Ubuntu-4ubuntu0.7, OpenSSL 1.0.2n 7 Dec 20172、安装依赖,依次执行以下命令 sudo apt update sudo apt install build-essential zlib1g…...

python中可以处理word文档的模块:docx模块
前言 大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 话不多说,直接开搞,如果有什么疑惑/资料需要的可以点击文章末尾名片领取源码 一.docx模块 Python可以利用python-docx模块处理word文档,处理方式是面向对象的。 也就是说python-docx模块…...

TikTok或将于8月底关闭半闭环、速卖通或将推出“半托管”模式
《出海周报》是运营坛为外贸企业主和外贸人独家打造的重要资讯栏目,聚焦企业出海、海外市场动态、海外监管政策等方面,以简捷的方式,提升读者获取资讯的效率。 接下来运营坛为大家带来第15期出海周报,快来看看这周国内外市场发生了…...

《凤凰架构》第二章——访问远程服务
前言 这章挺难的,感觉离我比较远,不太好懂,简单记录吧。 这章主要讲访问远程服务,主要对比了RPC和REST的区别,可以结合知乎上的文章《既然有 HTTP 请求,为什么还要用 RPC 调用?》 这篇文章进行…...
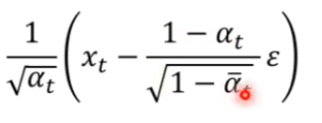
【Diffusion】李宏毅2023机器学习Diffusion笔记
文章目录 1 想法概述2 实际过程阶段1 Add Noise阶段2 Denoise 3 数学原理4 为什么推理时要额外加入noise5 一些不知道对不对的Summary 1 想法概述 从一张充满噪声的图中不断denoise,最终得到一张clear的图片。为了确定当前图片中噪声占比的大小,同时输入…...

CloudEvents—云原生事件规范
我们的系统中或多或少都会用到如下两类业务技术: 异步任务,用于降低接口时延或削峰,提升用户体验,降低系统并发压力;通知类RPC,用于微服务间状态变更,用户行为的联动等场景; 以上两种…...

神经网络基础-神经网络补充概念-51-局部最优问题
概念 局部最优问题是在优化问题中常见的一个挑战,特别是在高维、非凸、非线性问题中。局部最优问题指的是算法在优化过程中陷入了一个局部最小值点,而不是全局最小值点。这会导致优化算法在某个局部区域停止,而无法找到更好的解。 解决方案…...

深度学习中,什么是batch-size?如何设置?
什么是batch-size? batch-size 是深度学习模型在训练过程中一次性输入给模型的样本数量。它在训练过程中具有重要的意义,影响着训练速度、内存使用以及模型的稳定性等方面。 以下是 batch-size 大小的一些影响和意义: 训练速度:较大的 bat…...
[保研/考研机试] KY26 10进制 VS 2进制 清华大学复试上机题 C++实现
题目链接: 10进制 VS 2进制http://www.nowcoder.com/share/jump/437195121691738172415 描述 对于一个十进制数A,将A转换为二进制数,然后按位逆序排列,再转换为十进制数B,我们称B为A的二进制逆序数。 例如对于十进制…...
JSP-学习笔记
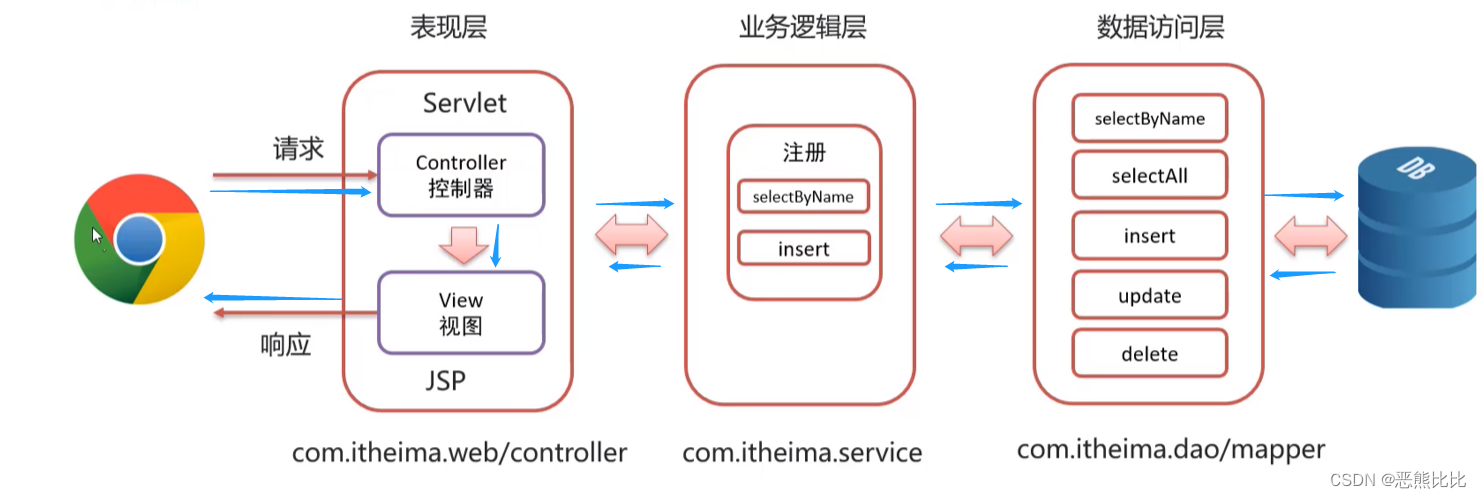
文章目录 1.JSP介绍2 JSP快速入门3 JSP 脚本3.1 JSP脚本案例3.2 JSP缺点 4 EL表达式4.1 快速入门案例 5. JSTL标签6. MVC模式和三层架构6.1 MVC6.2 三层架构 7. 案例-基于MVC和三层架构实现商品表的增删改查 1.JSP介绍 概念 JSP(JavaServer Pages)是一种…...
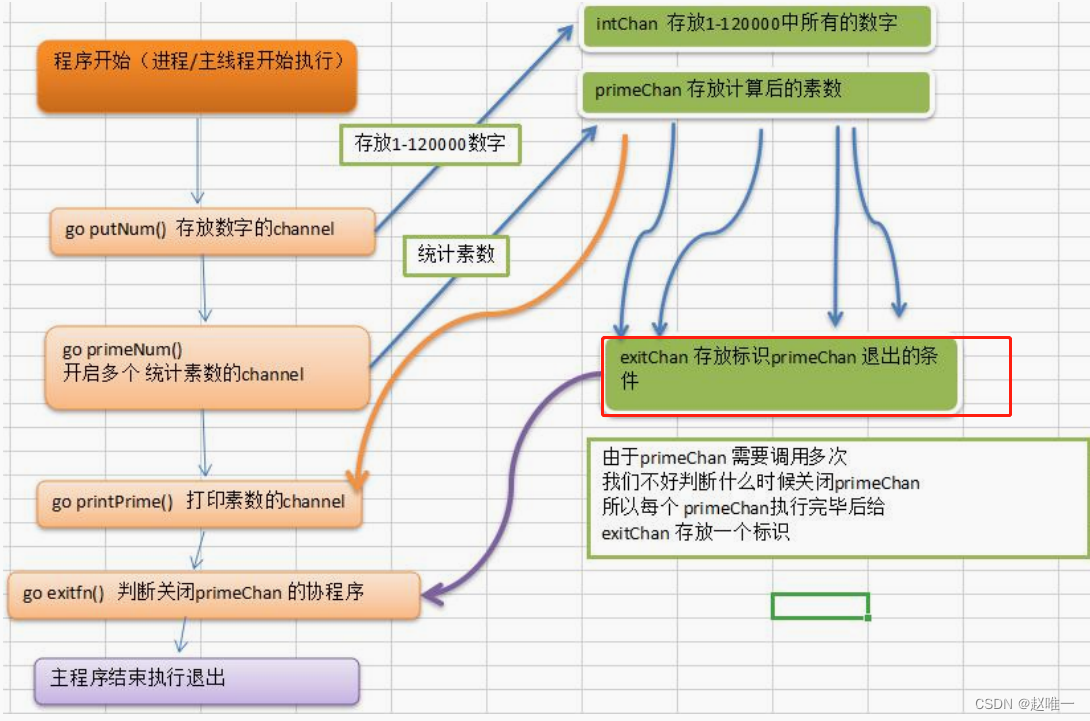
Golang协程,通道详解
进程、线程以及并行、并发 关于进程和线程 进程(Process)就是程序在操作系统中的一次执行过程,是系统进行资源分配和调度的基本单位,进程是一个动态概念,是程序在执行过程中分配和管理资源的基本单位,每一…...

unity 之 Vector 数据类型
文章目录 Vector 1Vector 2Vector 3Vector 4 Vector 1 在Unity中,Vector1 并不是一个常见的向量类型。 如果您需要表示标量(单个值)或者只需要一维的数据,通常会直接使用浮点数(float)或整数(in…...

私密数据采集:隧道爬虫IP技术的保密性能力探究
作为一名专业的爬虫程序员,今天要和大家分享一个关键的技术,它能够为私密数据采集提供保密性能力——隧道爬虫IP技术。如果你在进行敏感数据采集任务时需要保护数据的私密性,那么这项技术将是你的守护神。 在进行私密数据采集任务时ÿ…...

使用git rebase 之后的如何恢复到原始状态
我们常常喜欢使用git rebase去切换分支提交代码,操作流程就是: 先切换分支:比如当前是master 我们修改了一堆代码产生一个commit id :5555555567777 那么我们常常比较懒就直接切换了:git checkout dev 然后呢?使用命令git rebase 5555555567777,想把这笔修改提交到d…...

matlab相机标定知识整理
matlab相机标定知识整理 单目相机标定 单目相机标定 内参矩阵:cameraParams.Intrinsics.K 或者 cameraParams.K旋转矩阵:cameraParams.RotationMatrices 有待确定 cameraParams.RotationVectors平移矩阵:cameraParams.TranslationVectors径向…...

win11安装ubuntu 子系统安装过程及注意事项
第一步 :安装系统必须组件 由于子系统是系统自带组件,需要安装软件支持 第二步:应用商店安装 ubuntu 编辑 编辑 这个时候打开会报错 第三步,运行linux子系统 选择Windows PowerShell 以管理员身份运行) 输入&#…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
