Floyd(多源汇最短路)
Floyd求最短路
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,边权可能为负数。
再给定 k 个询问,每个询问包含两个整数 x 和 y,表示查询从点 x 到点 y 的最短距离,如果路径不存在,则输出 impossible。
数据保证图中不存在负权回路。
输入格式
第一行包含三个整数 n,m,k
接下来 m 行,每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
接下来 k 行,每行包含两个整数 x,y表示询问点 x 到点 y 的最短距离。
输出格式
共 k 行,每行输出一个整数,表示询问的结果,若询问两点间不存在路径,则输出 impossible。
数据范围
1≤n≤200
1≤k≤n2
1≤m≤20000
图中涉及边长绝对值均不超过 10000
输入样例:
3 3 2
1 2 1
2 3 2
1 3 1
2 1
1 3
输出样例:
impossible
1
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=220,INF=0x3f3f3f3f;
int f[N][N];
int main()
{int n,m,K;cin>>n>>m>>K;memset(f,0x3f,sizeof f);for(int i=0;i<=n;i++) f[i][i]=0;while(m--){int x,y,z;cin>>x>>y>>z;f[x][y]=min(f[x][y],z);}for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)f[i][j]=min(f[i][j],f[i][k]+f[k][j]);}}while(K--){int a,b;cin>>a>>b;if(f[a][b]>=INF/2) cout<<"impossible"<<endl;else cout<<f[a][b]<<endl;}return 0;
}牛的旅行
农民John的农场里有很多牧区,有的路径连接一些特定的牧区。
一片所有连通的牧区称为一个牧场。
但是就目前而言,你能看到至少有两个牧区不连通。
现在,John想在农场里添加一条路径(注意,恰好一条)。
一个牧场的直径就是牧场中最远的两个牧区的距离(本题中所提到的所有距离指的都是最短的距离)。
考虑如下的两个牧场,每一个牧区都有自己的坐标:
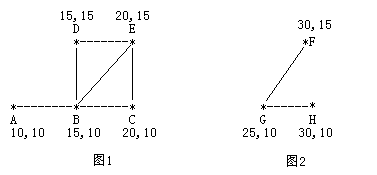
图 1 是有 5 个牧区的牧场,牧区用“*”表示,路径用直线表示。
图 1 所示的牧场的直径大约是 12.07106, 最远的两个牧区是 A 和 E,它们之间的最短路径是 A-B-E。
图 2 是另一个牧场。
这两个牧场都在John的农场上。
John将会在两个牧场中各选一个牧区,然后用一条路径连起来,使得连通后这个新的更大的牧场有最小的直径。
注意,如果两条路径中途相交,我们不认为它们是连通的。
只有两条路径在同一个牧区相交,我们才认为它们是连通的。
现在请你编程找出一条连接两个不同牧场的路径,使得连上这条路径后,所有牧场(生成的新牧场和原有牧场)中直径最大的牧场的直径尽可能小。
输出这个直径最小可能值。
输入格式
第 1 行:一个整数 N, 表示牧区数;
第 2 到 N+1 行:每行两个整数 X,Y, 表示 N 个牧区的坐标。每个牧区的坐标都是不一样的。
第 N+2 行到第 2*N+1 行:每行包括 N 个数字 ( 0或1 ) 表示一个对称邻接矩阵。
例如,题目描述中的两个牧场的矩阵描述如下:
A B C D E F G H
A 0 1 0 0 0 0 0 0
B 1 0 1 1 1 0 0 0
C 0 1 0 0 1 0 0 0
D 0 1 0 0 1 0 0 0
E 0 1 1 1 0 0 0 0
F 0 0 0 0 0 0 1 0
G 0 0 0 0 0 1 0 1
H 0 0 0 0 0 0 1 0
输入数据中至少包括两个不连通的牧区。
输出格式
只有一行,包括一个实数,表示所求答案。
数字保留六位小数。
数据范围
1≤N≤150
0≤X,Y≤10^5
输入样例:
8
10 10
15 10
20 10
15 15
20 15
30 15
25 10
30 10
01000000
10111000
01001000
01001000
01110000
00000010
00000101
00000010
输出样例:
22.071068直径最大值最小
题目的问题:给定两个联通块,在两个连通块中各取任意一点进行连接合成一个连通块,求合并后的联通块的最长路径的最小值
floyd:
这里可以分为两种情况:一种是在同一个连通分量,还有一种是不在同一个连通分量
1.在同一连通分量:
我们用maxd[i]表示和i所在连通分量的最长直径
那么这里的答案就是max1≤i≤nmaxd[i]max1≤i≤nmaxd[i]
2.不在同一连通分量:
我们可以用两个连通分量的maxd+它们之间的最短距离即可
这里的答案就是maxd[i]+get (i,j)+max[j]

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#define x first
#define y second
using namespace std;
typedef pair<int,int>PII;
const int N=200;
const double INF=1e20;
PII q[N];//存储n个牧场的坐标
char g[N][N];//存储n个牧场之间是否有边
double d[N][N];//存储n牧场之间的距离最下值
double dmax[N];//dmax[i]表示 i所在的连通分量的最长直径
int n;
//两个牧场之间的距离
double get_dist(PII a,PII b)
{double dx=b.x-a.x,dy=b.y-a.y;return sqrt(dx*dx+dy*dy);
}
int main()
{cin>>n;for(int i=0;i<n;i++) cin>>q[i].x>>q[i].y;for(int i=0;i<n;i++) cin>>g[i];for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(i!=j){if(g[i][j]=='1')d[i][j]=get_dist(q[i],q[j]);else d[i][j]=INF;}}}//floyd 得出d[i][j] 距离的最小值for(int k=0;k<n;k++){for(int i=0;i<n;i++){for(int j=0;j<n;j++){d[i][j]=min(d[i][j],d[i][k]+d[k][j]);}}}for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(d[i][j]<INF){dmax[i]=max(dmax[i],d[i][j]);}}}double ans1=0;//情况1for(int i=0;i<n;i++) ans1=max(ans1,dmax[i]);double ans2=INF;//情况2for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(d[i][j]>=INF){ans2=min(ans2,get_dist(q[i],q[j])+dmax[i]+dmax[j]);}}}printf("%.6lf\n",max(ans1,ans2));return 0;
}排序(传递闭包)
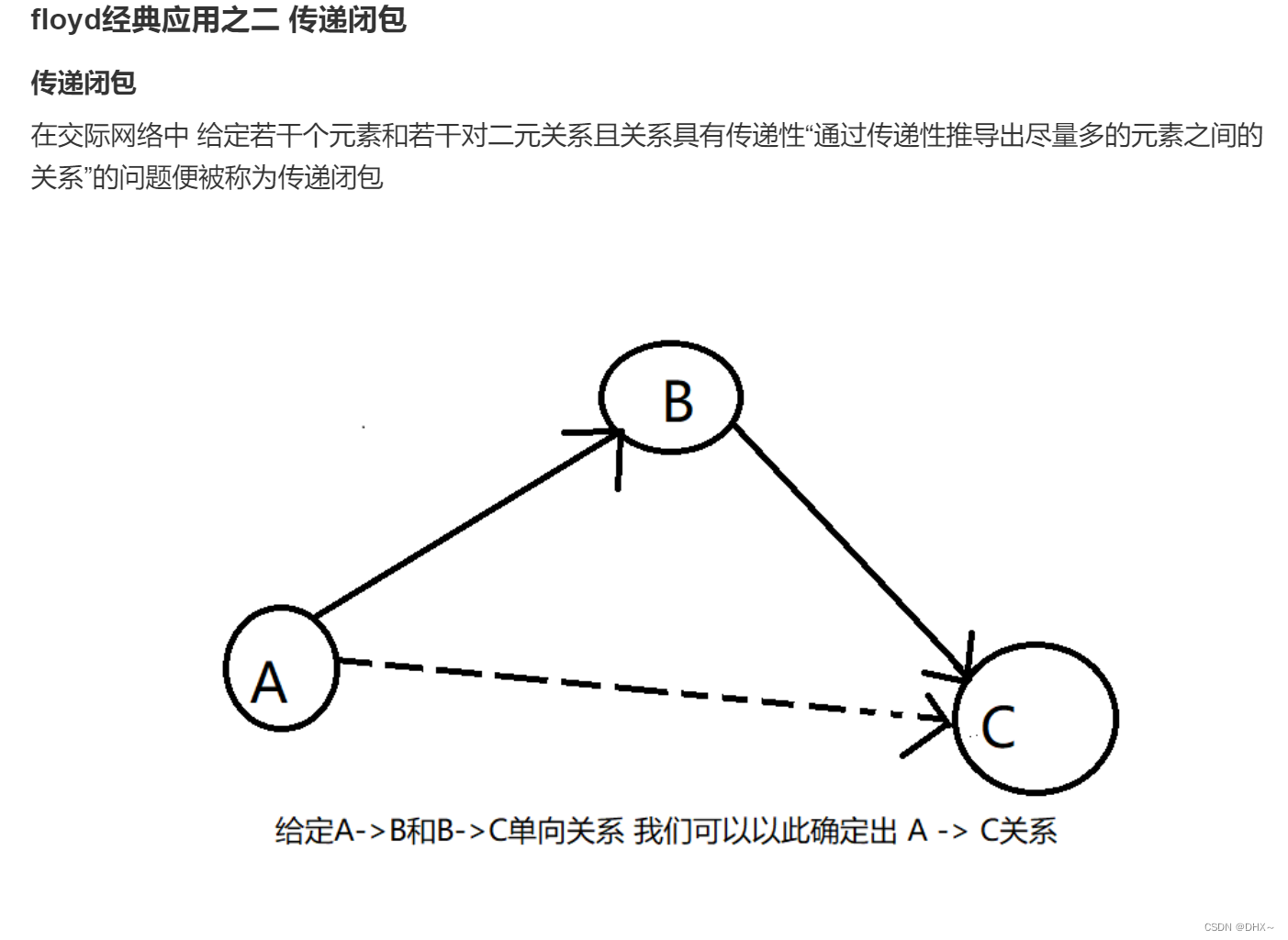
给定 n 个变量和 m 个不等式。其中 n 小于等于 26,变量分别用前 n 的大写英文字母表示。
不等式之间具有传递性,即若 A>B 且 B>C,则 A>C。
请从前往后遍历每对关系,每次遍历时判断:
- 如果能够确定全部关系且无矛盾,则结束循环,输出确定的次序;
- 如果发生矛盾,则结束循环,输出有矛盾;
- 如果循环结束时没有发生上述两种情况,则输出无定解。
输入格式
输入包含多组测试数据。
每组测试数据,第一行包含两个整数 n 和 m。
接下来 m 行,每行包含一个不等式,不等式全部为小于关系。
当输入一行 0 0 时,表示输入终止。
输出格式
每组数据输出一个占一行的结果。
结果可能为下列三种之一:
- 如果可以确定两两之间的关系,则输出
"Sorted sequence determined after t relations: yyy...y.",其中't'指迭代次数,'yyy...y'是指升序排列的所有变量。 - 如果有矛盾,则输出:
"Inconsistency found after t relations.",其中't'指迭代次数。 - 如果没有矛盾,且不能确定两两之间的关系,则输出
"Sorted sequence cannot be determined."。
数据范围
2≤n≤26,变量只可能为大写字母 A∼Z。
输入样例1:
4 6
A<B
A<C
B<C
C<D
B<D
A<B
3 2
A<B
B<A
26 1
A<Z
0 0
输出样例1:
Sorted sequence determined after 4 relations: ABCD.
Inconsistency found after 2 relations.
Sorted sequence cannot be determined.
输入样例2:
6 6
A<F
B<D
C<E
F<D
D<E
E<F
0 0
输出样例2:
Inconsistency found after 6 relations.
输入样例3:
5 5
A<B
B<C
C<D
D<E
E<A
0 0
输出样例3:
Sorted sequence determined after 4 relations: ABCDE. 

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=30;
bool g[N][N],d[N][N];
bool st[N];
int n,m;
void floyd()//通过floyd 来逐渐判断两个点的连通情况
{memcpy(d,g,sizeof d);for(int k=0;k<n;k++)for(int i=0;i<n;i++)for(int j=0;j<n;j++)if(!d[i][j]) d[i][j]=d[i][k]&d[k][j];}
int check()
{for(int i=0;i<n;i++)//矛盾情况 A<Aif(d[i][i]) return 2;for(int i=0;i<n;i++)for(int j=0;j<i;j++)//不能确定情况if(!d[i][j]&&!d[j][i]) return 0;//可以确定情况return 1;
}
char get_min()//每次取出最小值
{for(int i=0;i<n;i++){if(!st[i])//如果没有取出 {bool flag=true;for(int j=0;j<n;j++)//判断是否 最小{if(!st[j]&&d[j][i]) {flag=false;break;}}if(flag){st[i]=true;return 'A'+i;}}}
}
int main()
{while(cin>>n>>m,n||m){memset(g,0,sizeof g);int type=0,t;// t 记录轮次 type记录判断出来与否的标志for(int i=1;i<=m;i++){char str[10];cin>>str;int a=str[0]-'A',b=str[2]-'A';if(!type){g[a][b]=1;floyd();type=check();if(type) t=i;}}if(!type) cout<<"Sorted sequence cannot be determined."<<endl;else if(type==2)printf("Inconsistency found after %d relations.\n",t);else{memset(st,0,sizeof st);printf("Sorted sequence determined after %d relations: ",t);for(int i=0;i<n;i++) printf("%c",get_min());printf(".\n");}}return 0;
}
相关文章:

Floyd(多源汇最短路)
Floyd求最短路 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,边权可能为负数。 再给定 k 个询问,每个询问包含两个整数 x 和 y,表示查询从点 x 到点 y 的最短距离,如果路径不存在,则输出 impo…...
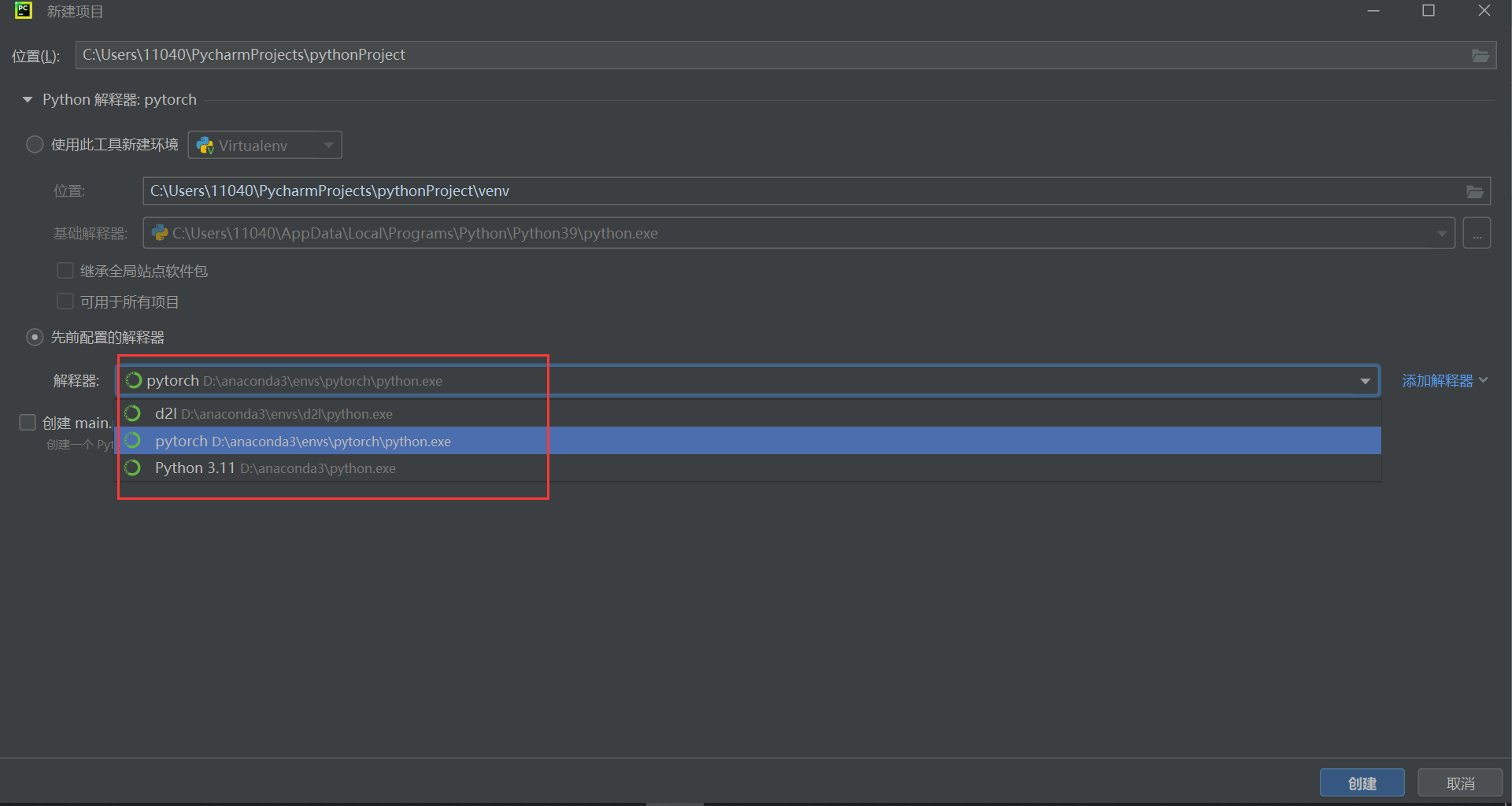
Pycharm找不到Conda可执行文件路径(Pycharm无法导入Anaconda已有环境)
在使用Pycharm时发现无法导入Anaconda创建好的环境,会出现找不到Conda可执行文件路径的问题。 解决 在输入框内输入D:\anaconda3\Scripts\conda.exe,点击加载环境。 注意前面目录是自己Anaconda的安装位置,之后就可以找到Anaconda的现有环…...

国产之光:讯飞星火最新大模型V2.0
大家好,我是herosunly。985院校硕士毕业,现担任算法研究员一职,热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名,CCF比赛第二名,科大讯飞比赛第三名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的…...
通讯录实现【C语言】
目录 前言 一、整体逻辑分析 二、实现步骤 1、创建菜单和多次操作问题 2、创建通讯录 3、初始化通讯录 4、添加联系人 5、显示联系人 6、删除指定联系人 7、查找指定联系人 8、修改联系人信息 9、排序联系人信息 三、全部源码 前言 我们上期已经详细的介绍了自定…...

pcl欧式聚类
欧式聚类实现方法大致是: 1、找到空间中某点 p 1 p_1 p1,用KD-Tree找到离他最近的n个点,判断这n个点到 p 1 p_1 p1的距离。将距离小于阈值r的点 p 2 、 p 3 、 p 4 p_2、p_3、p_4 p2、p3、p4…放在类Q里 2、在 Q ( p 1 ) Q(p_1…...
macOS Ventura 13.5.1(22G90)发布(附黑/白苹果系统镜像地址)
系统镜像下载:百度:黑果魏叔 系统介绍 黑果魏叔 8 月 18 日消息,苹果今日向 Mac 电脑用户推送了 macOS 13.5.1 更新(内部版本号:22G90),本次更新距离上次发布隔了 24 天。 本次更新重点修复了…...

分布式监控平台——Zabbix
市场上常用的监控软件: 传统运维:zabbix、 Nagios 一、zabbix概述 作为一个运维,需要会使用监控系统查看服务器状态以及网站流量指标,利用监控系统的数据去了解上线发布的结果,和网站的健康状态。 利用一个优秀的监…...
【OpenGauss源码学习 —— 列存储(创建表)】
列存储 什么是列存储?语法实现语法格式参数说明示例源码分析(创建表)语法层(Gram.y)子模块(utility.cpp) 总结 声明:本文的部分内容参考了他人的文章。在编写过程中,我们…...
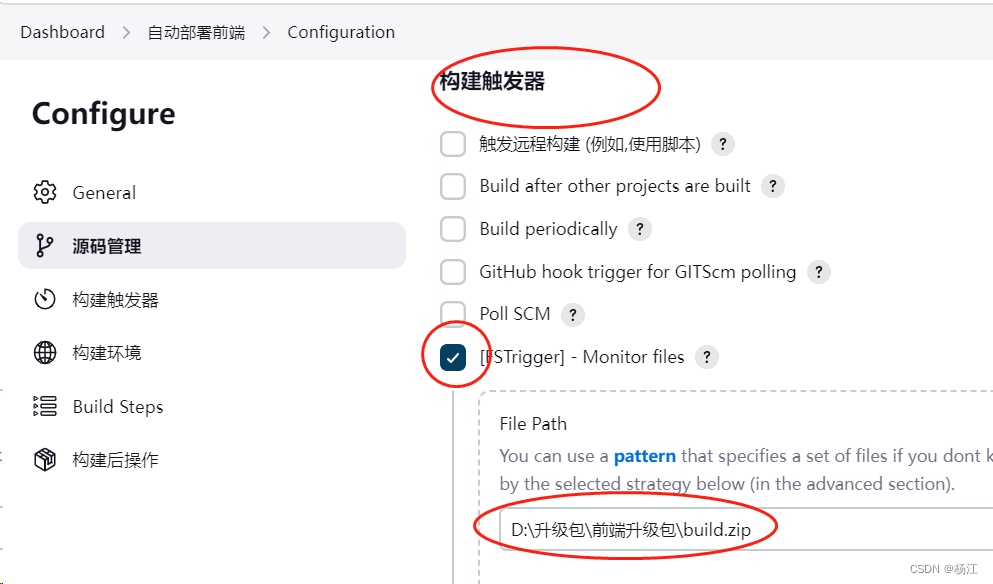
Jenkins 监控dist.zip文件内容发生变化 触发自动部署
为Jenkins添加plugin http://xx:xx/manage 创建一个任务 构建触发器 每3分钟扫描一次,发现指定文件build.zip文件的MD5发生变化后 触发任务...
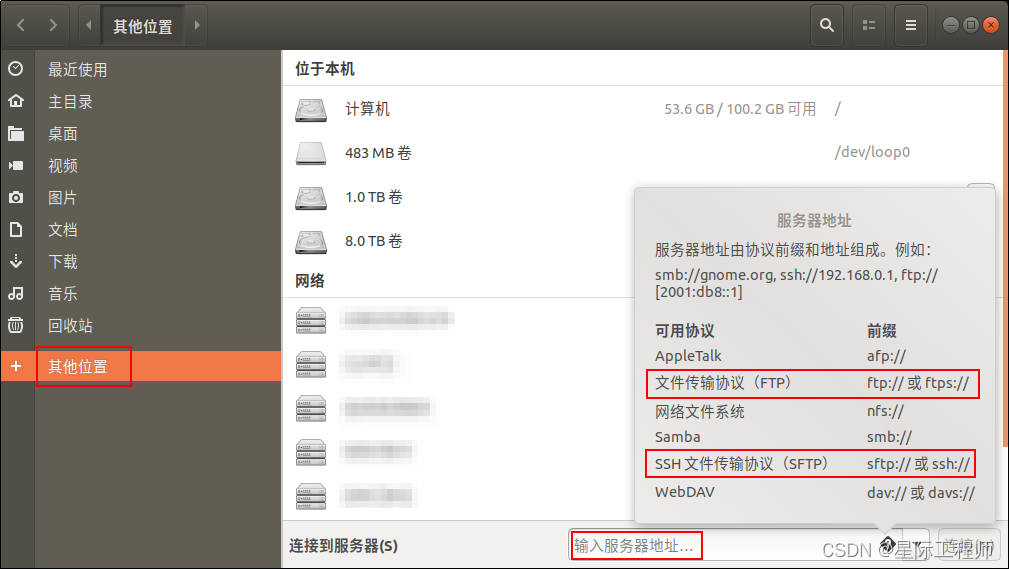
Linux系列讲解 —— FTP协议的应用
简单介绍一下FTP文件传输协议在linux系统中的应用。 目录 0. 基本概念1. FTP Server1.1 安装FTP Server1.2 FTP Server开启和关闭1.3 查看FTP Server是否开启1.4 FTP服务器配置 2. FTP Client2.1 lftp2.2 ftp2.3 sftp2.4 文件资源管理器集成的ftp和sftp 3. ftp常用命令 0. 基本…...

Rancher-RKE-install 部署k8s集群
一、为什么用Rancher-RKE-install 1.CNCF认证的k8s安装程序。 2.有中文文档。 二、安装步骤 1.下载Rancher-Rke的二进制包-下面是项目的地址 GitHub - rancher/rke: Rancher Kubernetes Engine (RKE), an extremely simple, lightning fast Kubernetes distrib…...

PHP8的正则表达式-PHP8知识详解
在网页程序的时候,经常会有查找符合某些复杂规则的字符串的需求。正则表达式就是描述这些规则的工具。 正则表达式是把文本或者字符串按照一定的规范或模型表示的方法,经常用于文本的匹配操作。 例如:我们在填写手机号码的时候,…...
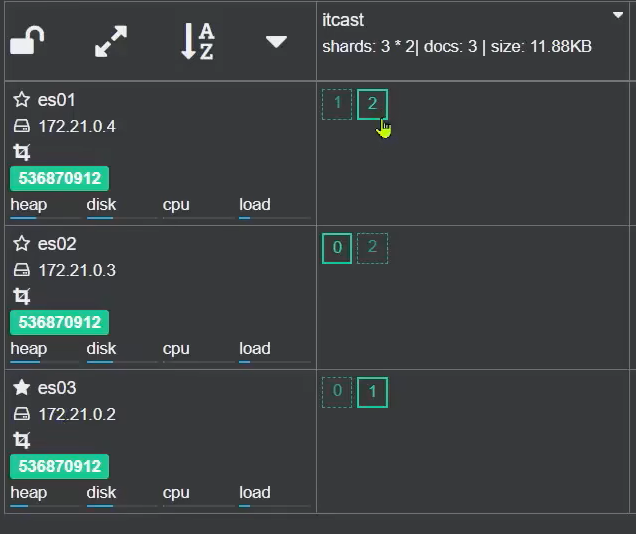
SpringCloud实用篇7——深入elasticsearch
目录 1 数据聚合1.1 聚合的种类1.2 DSL实现聚合1.2.1 Bucket聚合语法1.2.2 聚合结果排序1.2.3 限定聚合范围1.2.4 Metric聚合语法1.2.5.小结 1.3 RestAPI实现聚合1.3.1 API语法1.3.2 业务需求1.3.3 业务实现 2 自动补全2.1 拼音分词器2.2 自定义分词器2.3 自动补全查询2.4 实现…...

uni-app 经验分享,从入门到离职(二)—— tabBar 底部导航栏实战篇
文章目录 📋前言⏬关于专栏 🎯关于小程序 tabbar 的一些知识🎯创建一个基本的 tabBar📝最后 📋前言 这篇文章的内容主题是关于小程序的 tabBar 底部导航栏的入门使用和实战技巧。通过上一篇文章的基础,我们…...
:内存区域)
Java虚拟机(JVM):内存区域
一、内存区域介绍 Java虚拟机(JVM)内存可以分为以下几个区域: 程序计数器(Program Counter Register):用于记录当前线程执行的字节码指令的地址,属于线程私有的区域。在任意时刻,一…...
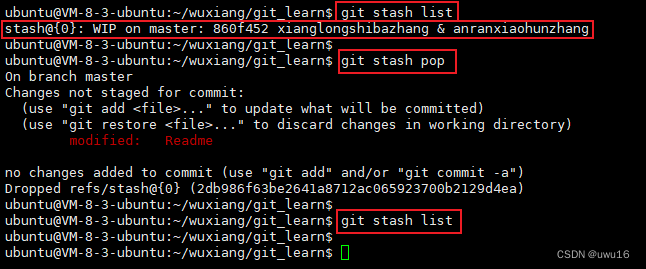
11 - git stash 开发中临时加塞了紧急任务怎么处理
查看所有文章链接:(更新中)GIT常用场景- 目录 文章目录 开发中临时加塞了紧急任务怎么处理 开发中临时加塞了紧急任务怎么处理 当你此时工作区已经修改了 Readme 文件,然后突然需要解决其他问题(紧急问题、新任务&…...
高效的WMS系统手持盘点方案
WMS系统手持盘点就是指利用WMS系统支持的手持式电子盘点设备进行库存盘点的方式。 具体来说: - 手持盘点设备是一种小型的电子设备,具有移动条形码扫描功能,可以实时与WMS系统联通。 - WMS系统利用手持设备,可以给仓储人员下发具体的盘点任务,例如需要盘点的货位、商品等信息…...

Oracle分页技术
1、使用两层嵌套 SELECT *FROM (SELECT A.*, ROWNUM RNFROM (SELECT * FROM edw_t100_bal_all) AWHERE ROWNUM < 40)WHERE RN > 21; 2、使用between..and.. SELECT *FROM (SELECT A.*, ROWNUM RN FROM (SELECT * FROM edw_t100_bal_all) A)WHERE RN between 21 and 40…...

2023-08-15 Untiy进阶 C#知识补充6——C#7主要功能与语法
文章目录 一、字面值改进二、out 内部声明 / 弃元三、ref 返回值四、本地函数五、抛出表达式六、元组七、模式匹配 注意:在此仅提及 Unity 开发中会用到的一些功能和特性,对于不适合在 Unity 中使用的内容会忽略。 C# 7 对应 Unity 版本࿱…...
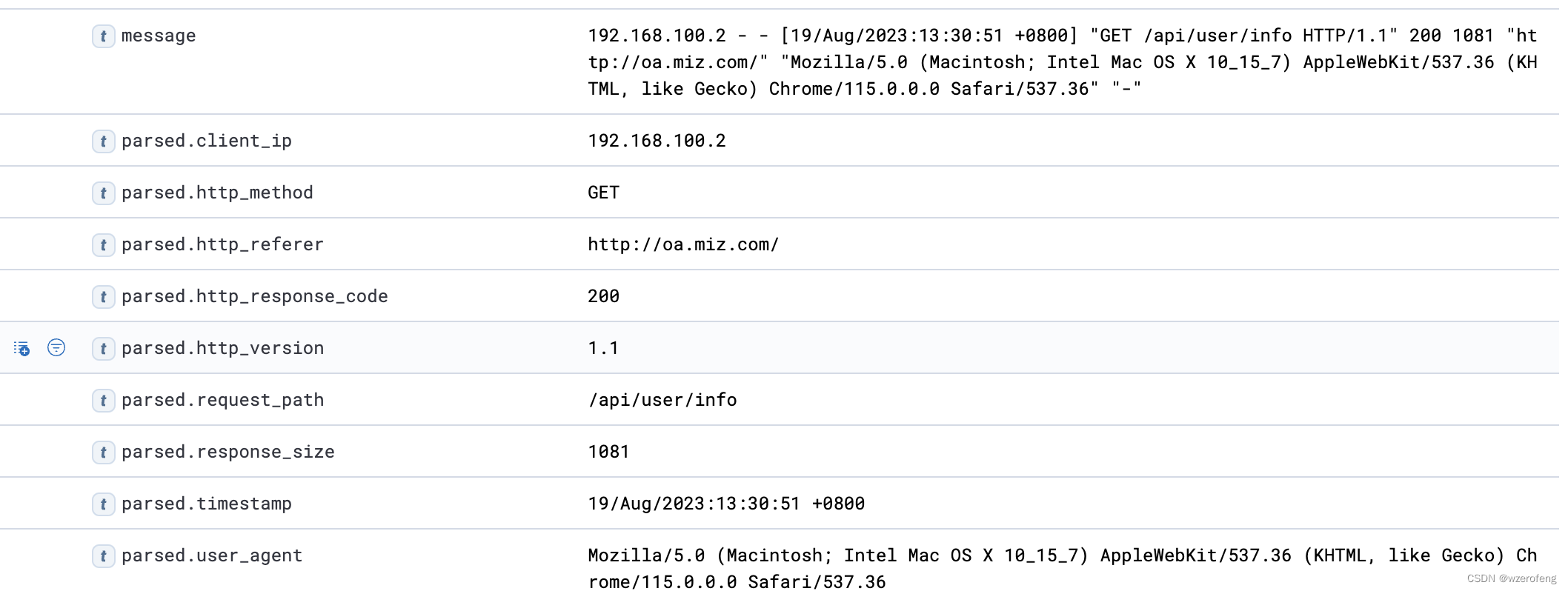
logstash配置文件
input { kafka { topics > “xxxx” bootstrap_servers > “ip:port” auto_offset_reset > “xxxx” group_id > “xxxx” consumer_threads > 3 codec > “json” } } filter { grok { match > { “message” > ‘%{IP:client_ip} - - [%{HTTPDATE:…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
