深入理解【二叉树】
📙作者简介: 清水加冰,目前大二在读,正在学习C/C++、Python、操作系统、数据库等。
📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。
欢迎点赞 👍 收藏 ⭐留言 📝 如有错误还望各路大佬指正!
✨每一次努力都是一种收获,每一次坚持都是一种成长✨

目录
前言
1. 特殊二叉树
1.1 满二叉树
1.2 完全二叉树
1.3 二叉树的性质
2. 搜索二叉树
3. 练习
📖 题目一
📖 题目二
📖 题目三
总结
前言
在计算机科学领域中,二叉树作为一种重要的数据结构,被广泛应用于各种算法和问题的解决方案中。然而,对于许多人来说,二叉树仍然是一个神秘而复杂的概念。本篇博客将带领你一同深入探索二叉树的内在结构和特性,帮助你建立起对二叉树的全面理解。
1. 特殊二叉树
前边我们已经介绍了树的结构,也了解了普通二叉树,以及二叉树的遍历,今天我们将会继续深入学习二叉树。
1.1 满二叉树
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。如下图:
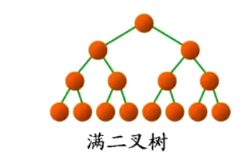
1.2 完全二叉树
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。(直白点说就是:假设有n层,前n-1层为满二叉树,最后一层的节点从左到右依次连接,不会出现一个节点连不满的情况)
如下图:
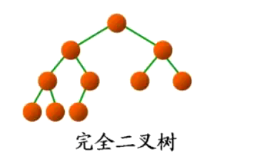
这样的它就不属于完全二叉树:
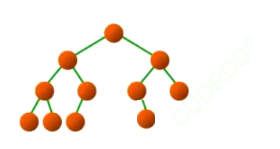
因为从左到右,有节点没有满(从左到右节点必须连满,不能出现有空)。
1.3 二叉树的性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 2⁽ⁱ⁻¹⁾个结点.
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2ʰ-1
- 对任何一棵二叉树, 如果度为0其叶结点个数为 , 度为2的分支结点个数为 ,则有 n₀=n₂+1(下标为二叉树的度)
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h= log₂(n+1)
对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
2. 搜索二叉树
上述的二叉树对于数据存储没什么特别规定与要求,属于普通二叉树大类,对于普通二叉树来说,没有增删查改,普通二叉树的增删查改在现实应用中是没有意义的(数据没有特殊规定,无法确认新增节点的位置)。所以这里我们再来介绍一下其他的二叉树——搜索二叉树
什么是搜索二叉树?如下图:
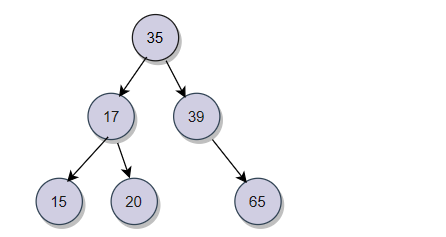
任何一颗树,左子树都要比根小,右子树都要比根大。搜索二叉树的这个特性使得它的插入位置就可以确定。例如我们要插入一个数据38:

从根开始,38比35大,就进入右子树,38比39小,那就插入到39左子树的位置。
例如我们再插入一个40:
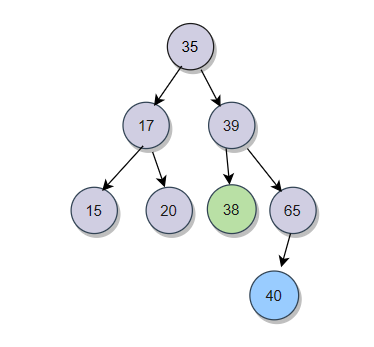
从根开始,40比35大,就进入右子树,40比39大,进入右子树,40比65小,那就插入到65的左孩子节点位置。
如果我们要查找一个数,例如我们查找30,30比35小,进入左子树,30比17大,进入右子树,30比20大继续进入到右子树,但20没有子节点,所以没有30这个节点,到这里就停止寻找。通过这些例子我们可以发现,这样的二叉树很适合搜索。搜索二叉树最多搜索高度次。
搜索的时间复杂度是O(N),细心的同学可能就会发现,搜素二叉树最多搜素高度次,那二叉树的高度不是有一个公式h= log₂(n+1),时间复杂度为什么不是O(log N)?
这里注意:这个二叉树的高度公式针对的是满二叉树,而搜素二叉树它可能出现退化的情况。如下图:
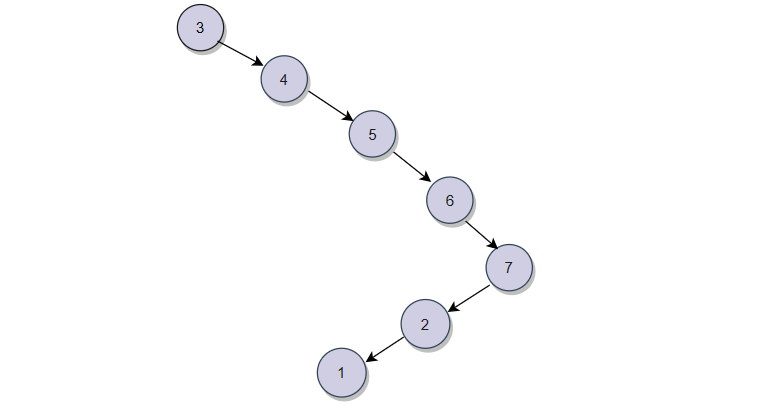
最坏的情况:我们找1这个节点,它的时间复杂度就是O(N)。
那要如何避免这种情况的发生?使左右两边的节点数量均匀,又要保持这个特性。
这里又可以引出一个新的概念——平衡树
平衡树的特性就是:左右两边的节点数据比较均匀。
平衡树又可以分为:
- AVL树
- 红黑树
依照现在博客所讲的水平,想要学会这两种树是不可能的,除此之外后续我们还会学习B树,它是一种多叉搜索树。数据库的原理就与它有关。(此部分为了解)这部分的树状结构才是有用的东西,精髓就在这部分内容,这里我们后续会进行学习。
本期我们不会进行代码的编写介绍,我们要弄清楚二叉树的性质,以及延申部分。接下来就是练习部分,帮助大家理解掌握二叉树的性质。
3. 练习
📖 题目一
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为 ()
A、不存在这样的二叉树
B、200
C、198
D、199
✨题目解析:
度为2的节点有199个,根据二叉树的性质:n₀=n₂+1,度为0的节点个数等于度为2的节点个数+1。度为0的节点就为叶子节点。
正确答案:B
📖 题目二
2. 在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A、n
B、n+1
C、n-1
D、n/2
✨题目解析:
这道题目看似无解,突破口就在完全二叉树。我们设度为0的节点个数为N0,度为1的节点个数为N1,度为2的节点个数为N2。根据性质可知:N0=N2+1,且N0+N1+N2=2n。
两式联合:N0+N1+N0-1=2n。
又因为这是一颗完全二叉树,完全二叉树度为1的节点只能有1个或没有。但又要确保都为整数,所以度为1的节点就只要1个。即:N0+1+N0-1=2n
正确答案:A
📖 题目三
3.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A、11
B、10
C、8
D、12
✨题目解析:
题目要求这棵树的高度,那就设树的高度为h,最后一层缺了X个,根据定义我们可知:满二叉树是一种特殊的完全二叉树。
由此可得出:2^h-1-X就是完全二叉树的节点个数,即:2^h-1-X=531。到这里看似无解,但我们还可以根据性质进行推算,X的取值范围是0 ~ 2^(h-1)-1,至少最后一层有1个节点,最多最后一次为满(满二叉树),知道这些我们就可以带选项进行推算了。代换:2^h-1-2^(h-1)+1。代入选项,看最终哪个选项的结果最接近500。
代入11,2的11次方:2048-1024=1024,如果高度是11那最少有1024个节点,A选项错误。这样依次代入。
正确答案:B
总结
通过本篇博客我们对二叉树的内在结构、特性,有了更全面的了解,希望通过本篇博客的阅读,你已经掌握了深入理解二叉树的关键知识。最后,感谢阅读!
相关文章:

深入理解【二叉树】
📙作者简介: 清水加冰,目前大二在读,正在学习C/C、Python、操作系统、数据库等。 📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。 欢迎点赞 👍…...
RequestRespons
文章目录 Request&Respons1 Request和Response的概述2 Request对象2.1 Request继承体系2.2 Request获取请求数据2.2.1 获取请求行数据2.2.2 获取请求头数据2.2.3 获取请求体数据2.2.4 获取请求参数的通用方式 2.3 IDEA快速创建Servlet2.4 请求参数中文乱码问题2.4.1 POST请…...

UniApp 使用命令创建页面的详细指南
系列文章目录 文章目录 系列文章目录前言一、安装Uni-CLI二、创建页面三、页面创建命令四、页面结构五、页面使用总结 前言 UniApp是一款跨平台的前端框架,可以用于开发同时运行在多个平台(如微信小程序、H5、App等)的应用程序。本文将详细介…...

Opencv 图像的读取与写入
目录 导入cv2 读取图像数据 创建一个窗口 waitKey方法 关闭所有窗口 完整示例 保存图片 示例 导入cv2 # 导入opencv包 import cv2 读取图像数据 cv2.imread(path, flag) 参数说明: path:要读取的图像文件的路径。 flag(可选&#…...

关于rinex3.x广播星历文件中时间系统的说明
文章目录 rinex广播星历文件介绍广播星历介绍rinex3.x多系统广播星历文件中的时间系统写在最后 rinex广播星历文件介绍 rinex星历文件是一种ascii字符文件,可以存放广播星历和精密星历,被广泛用于GNSS数据处理。 本文主要介绍广播星历文件。 对于rinex…...

Ansible 实战
Ansible 实战 1. httpd 角色 目录 rootubuntu1904:~#tree -f httpd/ httpd ├── httpd/default │ └── httpd/default/main.yml ├── httpd/files │ ├── httpd/files/httpd.conf │ └── httpd/files/index.html ├── httpd/handlers │ └── http…...

三、单元测试
三、单元测试 好的单元测试必须遵守 AIR 原则 A:Automatic(自动化)I:Independent(独立性)R:Repeatable(可重复) 单元测试应该是全自动执行的,并且非交互式的…...
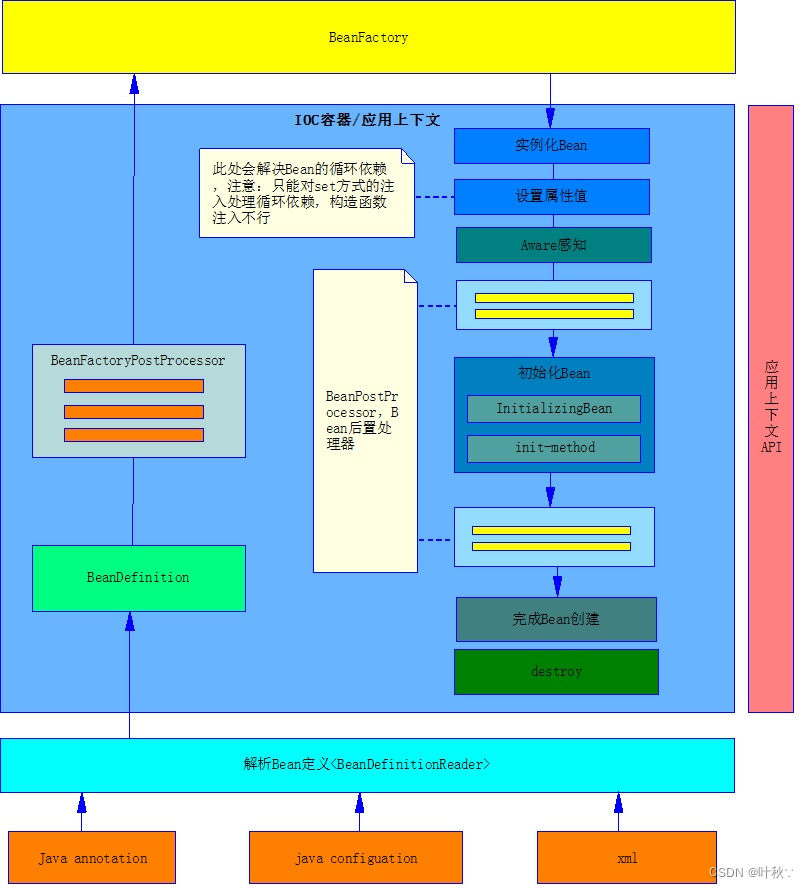
“Spring管理JavaBean的过程及Bean的生命周期“
目录 引言1.弹簧容器2. Bean的生命周期2.1 配置javaBean2.2. 解析Bean的定义2.3 检查是否需要添加自己的功能2.4 初始化2.5 实现Aware接口2.6 扩展2.7. 销毁 3. 单例模式和原型模式3.1. 单例模式3.2. 原型模式 4. 总结 引言 Spring框架是一个非常流行的Java应用程序框架&#…...
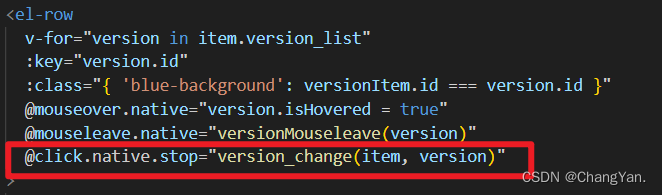
@mouseover不起作用,并没有触发
我的错误代码如下: <el-rowv-for"version in item.version_list":key"version.id":class"{ blue-background: versionItem.id version.id }"mouseover.native"version.isHovered true"mouseleave.native"version…...

Vue 2 组件注册
组件名的命名规则 定义组件名的两种方式: 短横线分隔命名,Kebab Case,例如my-component-name。单词首字母大写命名,Pascal Case,例如MyComponentName。 第一种方式在模板中使用<my-component-name>引用该元素…...

学习游戏开发引擎,打造梦想中的虚拟世界!
游戏开发引擎是游戏开发过程中的关键工具,它们提供了开发者所需的各种功能和资源,加速了游戏的制作过程。以下是一些常用的游戏开发引擎以及它们的优势: Unity(Unity3D): 优势: Unity 是目前最…...

AI搜索引擎助力科学家创新
开发者希望通过帮助科学家从大量文献中发现联系从而解放科学家,让他们专注于发现和创新。 图片来源:The Project Twins 对于专注于历史的研究者Mushtaq Bilal来说,他在未来科技中投入了大量时间。 Bilal在丹麦南部大学( Universit…...

神经网络基础-神经网络补充概念-50-学习率衰减
概念 学习率衰减(Learning Rate Decay)是一种优化算法,在训练深度学习模型时逐渐减小学习率,以便在训练的后期更加稳定地收敛到最优解。学习率衰减可以帮助在训练初期更快地靠近最优解,而在接近最优解时减小学习率可以…...
)
android.system.ErrnoException: open failed: EPERM (Operation not permitted)
android 10(Q)开始增加了沙盒机制,不能直接把文件保存到/sdcard目录下,只能保存到APP专属目录下;AndroidManifest.xml在标签下增加属性【android:requestLegacyExternalStorage“true”】可以暂时保存到/sdcard路径下,但是Android…...
基于 KubeSphere 的应用容器化在智能网联汽车领域的实践
公司简介 某国家级智能网联汽车研究中心成立于 2018 年,是担当产业发展咨询与建议、共性技术研发中心、创新成果转化的国家级创新平台,旨在提高我国在智能网联汽车及相关产业在全球价值链中的地位。 目前着力建设基于大数据与云计算的智能汽车云端运营…...
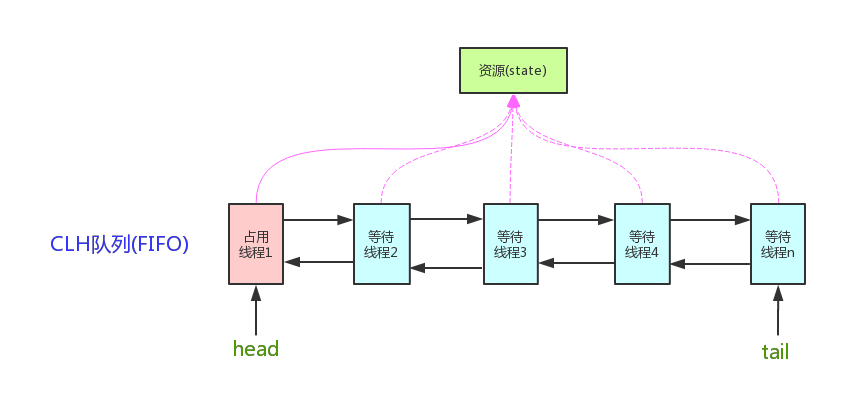
面试之ReentrantLock
一,ReentrantLock 1.ReentrantLock是什么? ReentrantLock实现了Lock接口,是一个可重入且独占式的锁,和Synchronized关键字类似,不过ReentrantLock更灵活,更强大,增加了轮询、超时、中断、公平锁…...

系统学习Linux-MongoDB
概述 mongodb是一个nosql数据库,它有高性能、无模式、文档型的特点。是nosql数据库中功能最丰富,最像关系数据库的。数据库格式为BSON 相关概念实例:系统上运行的mongodb的进程,类似于mysql实例;库:每个数…...
的介绍与创建)
【带着学Pytorch】2、张量(Tensor)的介绍与创建
一、Tensor介绍 1.1、 张量是什么? 最开始在出现CPU和GPU, GPU出现主要解决的问题时并行计算,在此基础上的软件层面的工作基本上围绕着并行计算进行的,张量也不例外。 首先,我们先来聊聊 编程语言,python,java ,C,C++等,他们都有的共同特点是什么?在大学中计算机类…...
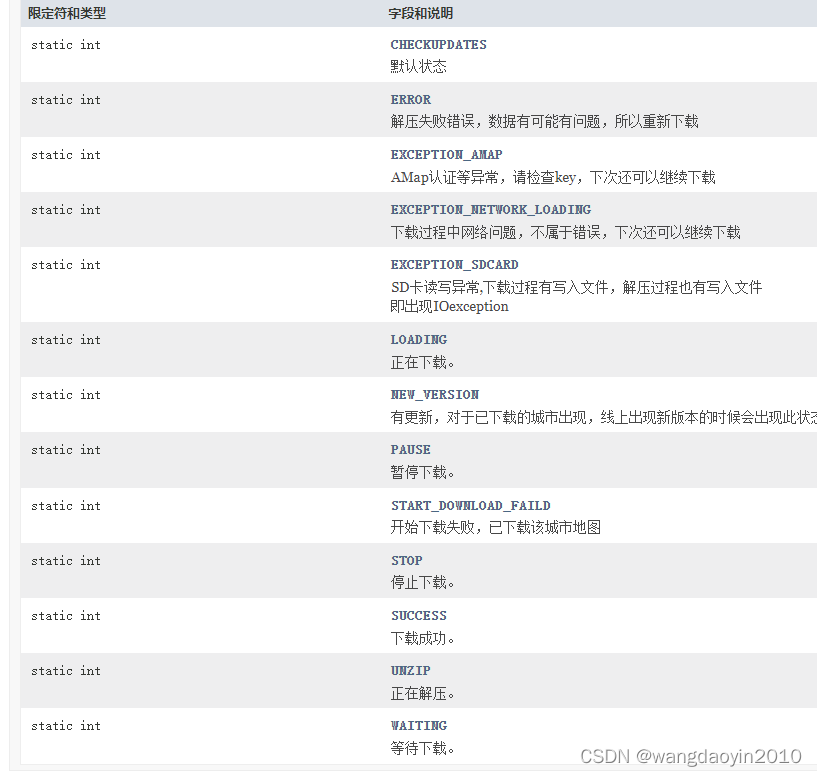
UniApp 制作高德地图插件
1、下载Uni插件项目 在Uni官网下载Uni插件项目,并参考官网插件项目创建插件项目. 开发者须知 | uni小程序SDK 如果下载下来项目运行不了可以参考下面链接进行处理 UniApp原生插件制作_wangdaoyin2010的博客-CSDN博客 2、引入高德SDK 2.1 在高德官网下载对应SD…...

C# 图像处理之灰色图转化为RGB图像
咨询通义千问的“C# 图像处理之灰色图转化为RGB图像”结果,看看如何: 在C#中,可以使用Image类来处理图像。要将灰色图像转换为RGB图像,可以按照以下步骤进行操作: 1.创建一个灰色图像对象。 Image grayImage Imag…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
