题解 | #1012.Equalize the Array# 2023杭电暑期多校10
1012.Equalize the Array
签到
题目大意
定义一个数组的 m o d e mode mode 是其中出现次数最多的数字(可不唯一)
给定一个数组 a a a ,每次操作可以选定其一个 m o d e mode mode 并使数组中所有与之相等的元素 + 1 +1 +1
问任意次操作后能否使数组中全部元素相等
解题思路
如果数组中最小的元素是 m o d e mode mode ,连续操作最小元素即可实现//
元素计数,判断最小元素出现次数是否最多即可
时间复杂度
O ( n log n ) O(n\log n) O(nlogn)
参考代码
参考代码为已AC代码主干,其中部分功能需读者自行实现
void solve()
{ll n;cin >> n;map<ll,ll> mp;ll t;FORLL(i,1,n){cin >> t;mp[t]++;}ll mxcnt=0,mxi=0,mn=0;FORLL(i,1,n){t=mp[i];if(!mn&&t) mn=i;if(t>mxcnt) {mxcnt=t;mxi=i;}}if(mxi<=mn) cout << YES;else cout << NO;
}
相关文章:

题解 | #1012.Equalize the Array# 2023杭电暑期多校10
1012.Equalize the Array 签到 题目大意 定义一个数组的 m o d e mode mode 是其中出现次数最多的数字(可不唯一) 给定一个数组 a a a ,每次操作可以选定其一个 m o d e mode mode 并使数组中所有与之相等的元素 1 1 1 问任意次操作后…...
)
UE4/5C++多线程插件制作(二十一、使用)
目录 DemoPawn.h DemoPawn.cpp 会出现的bug 插件 相关的插件制作在上一节已经完成了。 具体的使用方式在第0章已经写了,get之后去绑定即可。 而后笔者做了一个接口,具体的绑定方式也就在这个接口里面。 接下来最重要的是进行使用,对此我做了一个与蓝图相关的接口,里…...

【C#】关于?的用法
1、可空类型修饰符(?) 如: int? x null;//可空类型默认值都是null,而值类型如int默认值为0、bool默认值为false等 bool? result true;2、三目运算符(?:) 如: bool…...
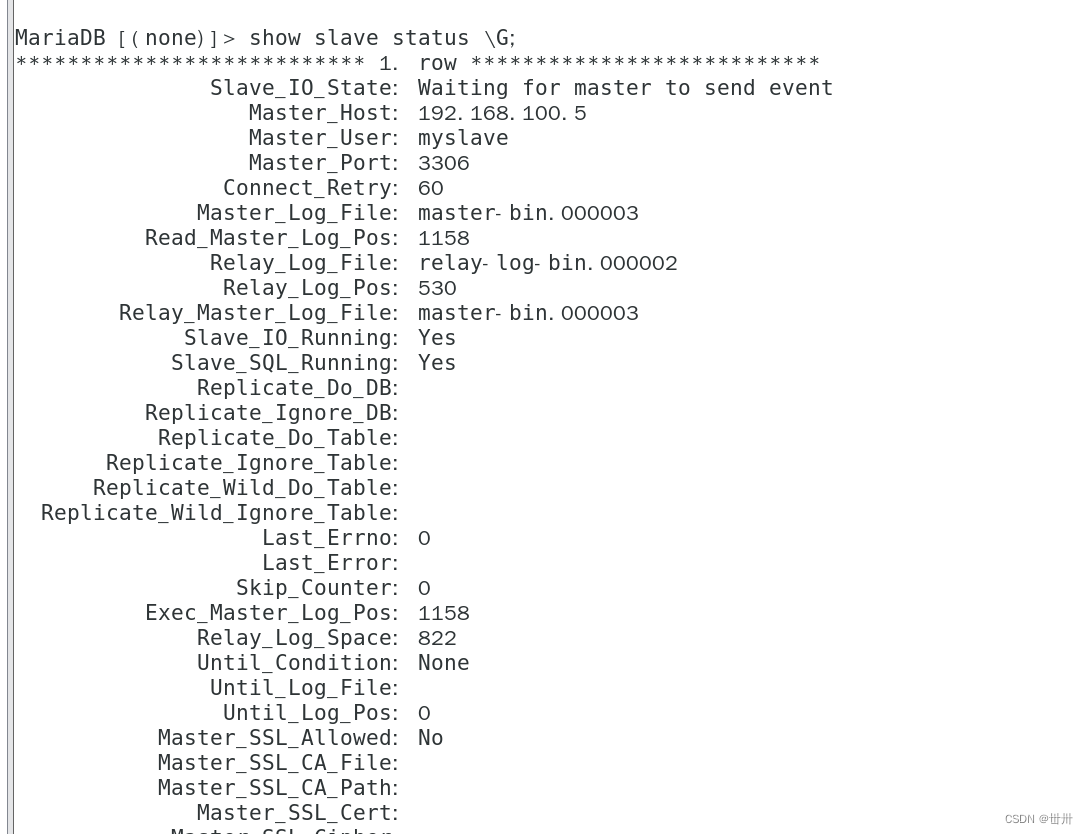
linux——mysql的高可用MHA
目录 一、概述 一、概念 二、组成 三、特点 四、工作原理 二、案例 三、构建MHA 一、基础环境 二、ssh免密登录 三、主从复制 master slave1 四、MHA安装 一、环境 二、安装node 三、安装manager 一、概述 一、概念 MHA(MasterHigh Availability&a…...

【学习日记】【FreeRTOS】空闲任务与阻塞延时
写在前面 本文是基于野火 RTOS 教程对空闲任务和阻塞延时的详解。 一、什么是任务中的阻塞延时 说到阻塞延时,笔者的第一反应就是在单片机的 while 循环中,使用一个 for 循环不断递减一个大数,通过 CPU 不断执行一条指令的耗时进行延时。这…...
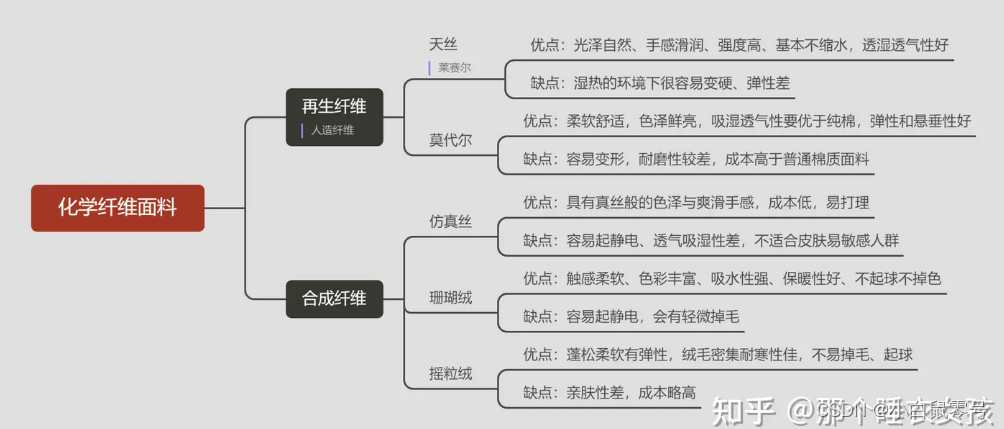
衣服材质等整理(时常更新)
参考文章&图片来源 https://zhuanlan.zhihu.com/p/390341736 00. 天然纤维 01. 化学纤维 02. 聚酯纤维(即,涤纶) 一种由有机二元酸和二元醇通过化学缩聚制成的合成纤维。具有出色的抗皱性和保形性,所制衣物在穿着过程中不容…...

电子商务环境下旅游价值链
迈克尔 ・ 波特(Michael E. Porter)在其《竞争优势》一书中提出了“价值链” 的概念,并认为一家企业最核心的竞争优势在于对价值链的设计。虽然迈克尔 ・ 波 特提出的价值链主要是针对企业内部的价值链,但他视价值链为一系列连续完成的 活动ÿ…...
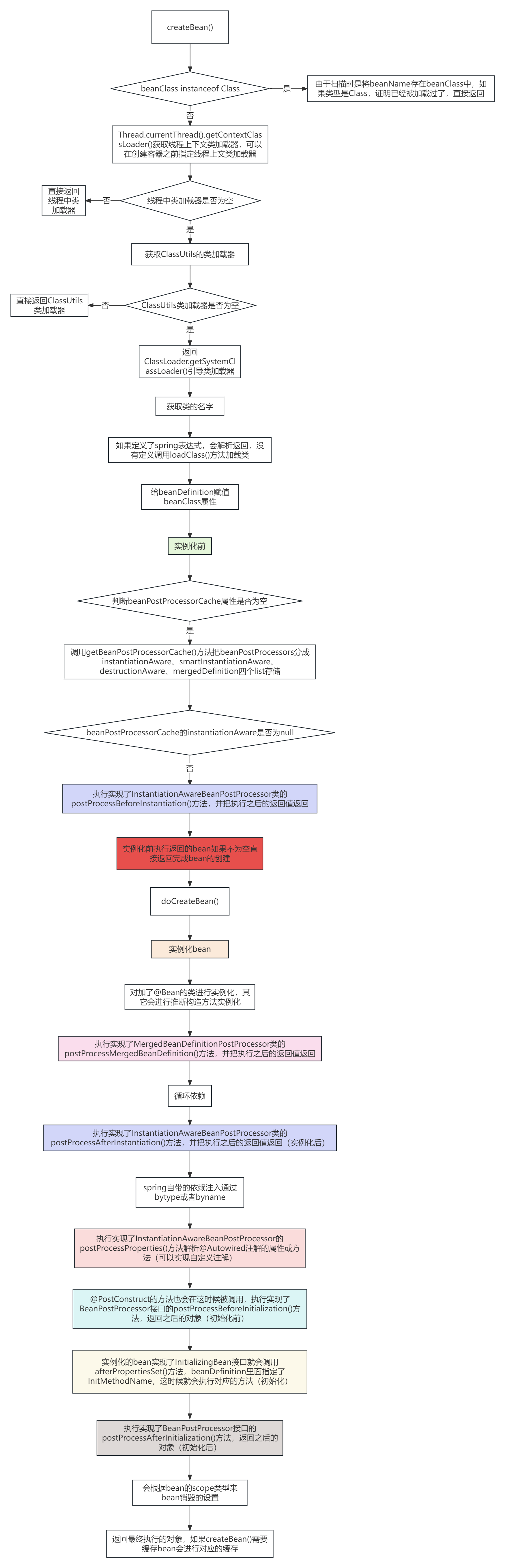
spring源码分析bean的生命周期(下)
doGetBean()执行过程 createBean()执行过程 一、DependsOn注解 spring创建对象之前会判断类上是否加了DependsOn注解,加了会遍历然后会添加到一个map中,spring会先创建DependsOn注解指定的类 二、spring类加载器 在合并BeanDefinition,确定…...
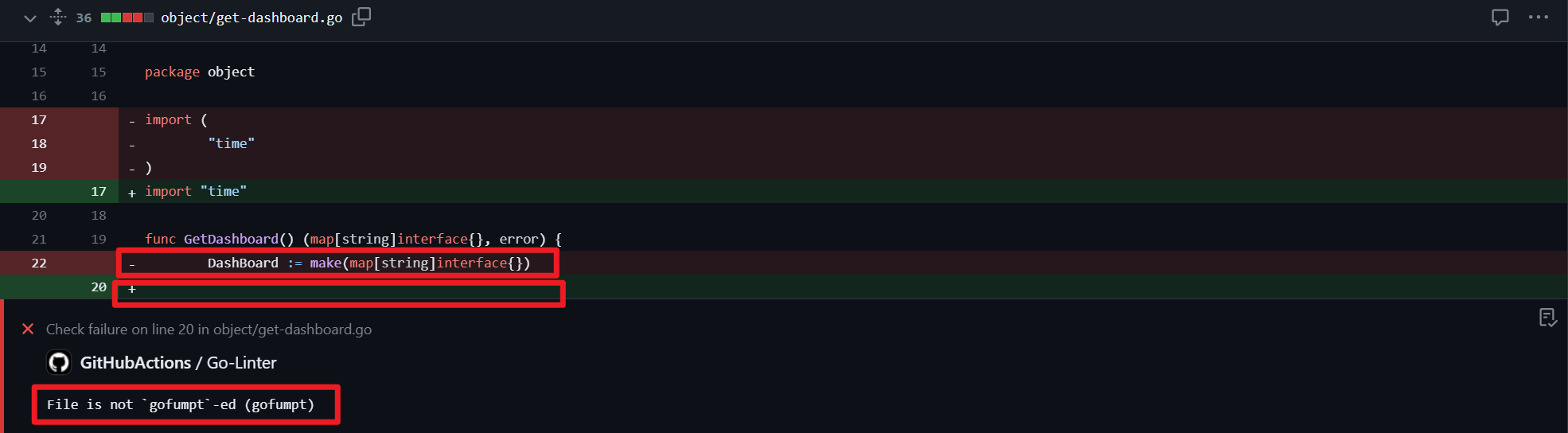
完美解决Github提交PR后报错:File is not gofumpt-ed (gofumpt)
问题阐述 最近在Github上提交PR后,遇到了这么一个问题:golangci-lint运行失败,具体原因是File is not gofumpt-ed (gofumpt)。 名词解释 golangci-lint: golangci-lint 是Go语言社区中常用的代码质量检查工具,它可以…...
pytorch3d成功安装
一、pytorch3d是什么? PyTorch3D的目标是帮助加速深度学习和3D交叉点的研究。3D数据比2D图像更复杂,在从事Mesh R-CNN和C3DPO等项目时,我们遇到了一些挑战,包括3D数据表示、批处理和速度。我们开发了许多有用的算子和抽象…...

【vue3】同个页面引入多个图表组件实现自适应的方法
首先说明,此方案仅针对vue3项目在同一个页面引入了多个图表组件,因为我发现不能框架不同的引入,resize的写法还不同 window.addEventListener("resize", function() {...// 在此处重新调用即可 }以下是具体写法: 循环…...
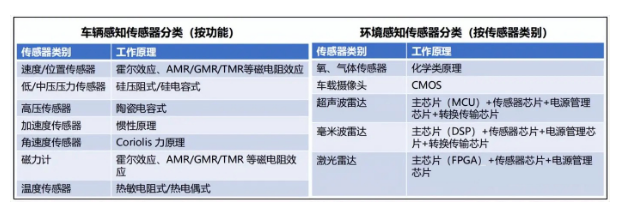
一文了解汽车芯片的分类及用途介绍
汽车芯片按其功能可分为控制类(MCU和AI芯片)、功率类、传感器和其他(如存储器)四种类型。市场基本被国际巨头所垄断。人们常说的汽车芯片是指汽车里的计算芯片,按集成规模可分为MCU芯片和AI芯片(SoC芯片&am…...
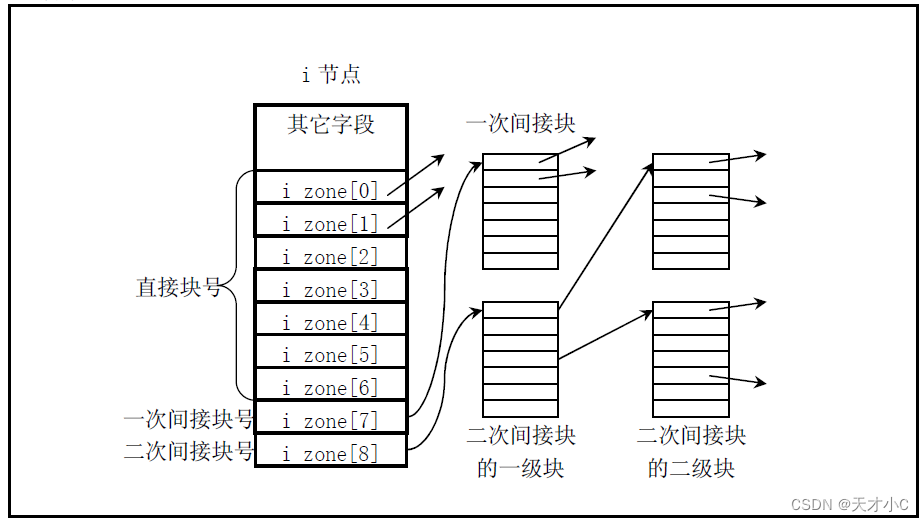
Linux0.11内核源码解析-truncate.c
truncate文件只要实现释放指定i节点在设备上占用的所有逻辑块,包括直接块、一次间接块、二次间接块。从而将文件节点对应的文件长度截为0,并释放占用的设备空间。 索引节点的逻辑块连接方式 释放一次间接块 static void free_ind(int dev,int block) {…...
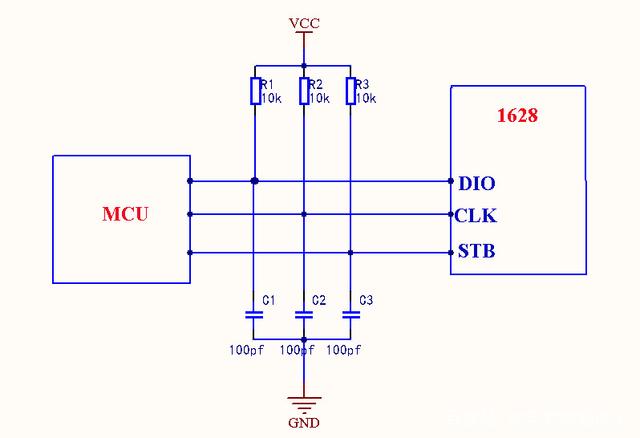
LED驱动型IC芯片的原理介绍
一、LED驱动器是什么 LED驱动器(LED Driver),是指驱动LED发光或LED模块组件正常工作的电源调整电子器件。由于LED PN结的导通特性决定,它能适应的电源电压和电流变动范围十分狭窄,稍许偏离就可能无法点亮LED或者发光效…...
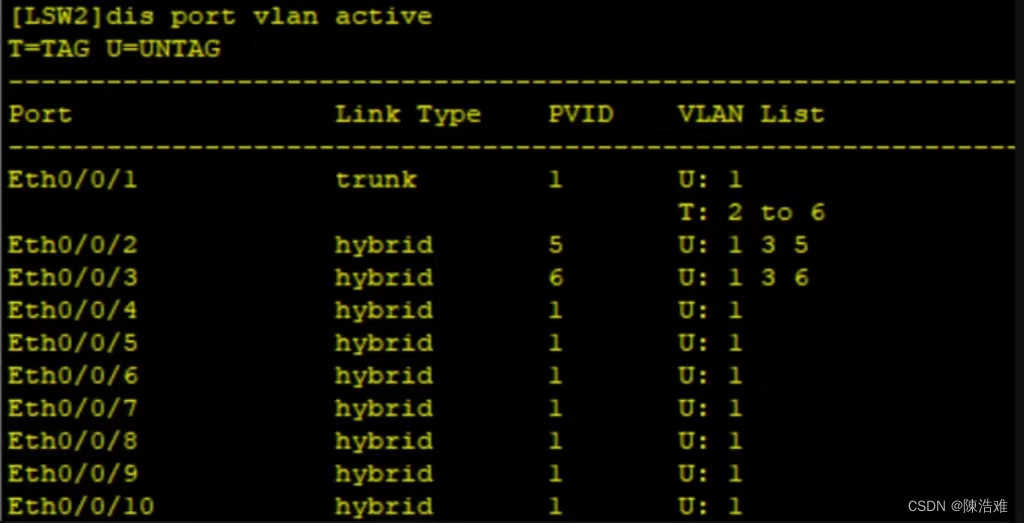
VLAN实验
实验题目如下: 实验拓扑如下: 实验要求如下: 【1】PC1/3的接口均为access模式,且属于van2,在同一网段 【2】PC2/4/5/6的IP地址在同一网段,与PC1/3不在同一网段 【3】PC2可以访问4/5/6,PC4不能…...

Qt应用开发(基础篇)——高级纯文本窗口 QPlainTextEdit
一、前言 QPlainTextEdit类继承于QAbstractScrollArea,QAbstractScrollArea继承于QFrame,是Qt用来显示和编辑纯文本的窗口。 滚屏区域基类https://blog.csdn.net/u014491932/article/details/132245486?spm1001.2014.3001.5501框架类QFramehttps://blo…...
三维可视化平台有哪些?Sovit3D可视化平台怎么样?
随着社会经济的发展和数字技术的进步,互联网行业发展迅速。为了适应新时代社会发展的需要,大数据在这个社会经济发展过程中随着技术的进步而显得尤为重要。同时,大数据技术的快速发展进程也推动了可视化技术的飞速发展,国内外各类…...

Xxl-job安装部署以及SpringBoot集成Xxl-job使用
1、安装Xxl-job: 可以使用docker拉取镜像部署和源码编译两种方式,这里选择源码编译安装。 代码拉取地址: https://github.com/xuxueli/xxl-job/tree/2.1.2 官方开发文档: https://www.xuxueli.com/xxl-job/#%E3%80%8A%E5%88%…...

【【超声波避障小车代码】】
超声波避障小车代码 #include <reg51.h> //通用51头文件 #include <intrins.h> //使用了_nop()_函数#define uchar unsigned char //用 uchar 表示 unsigned char 类型 #define uint unsigned int //用 uint 表示 unsigned int 类型sbit EN…...
)
TDI(Time Delay Integration)
TDI(Time Delay Integration)是一种特殊的图像采集技术,常用于线阵CCD(Charge-Coupled Device)相机。TDI技术可以在保持高分辨率的同时增强图像的信噪比(Signal-to-Noise Ratio, SNR)࿰…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...

【笔记】AI Agent 项目 SUNA 部署 之 Docker 构建记录
#工作记录 构建过程记录 Microsoft Windows [Version 10.0.27871.1000] (c) Microsoft Corporation. All rights reserved.(suna-py3.12) F:\PythonProjects\suna>python setup.py --admin███████╗██╗ ██╗███╗ ██╗ █████╗ ██╔════╝…...
