【机器学习】处理不平衡的数据集

一、介绍
假设您在一家给定的公司工作,并要求您创建一个模型,该模型根据您可以使用的各种测量来预测产品是否有缺陷。您决定使用自己喜欢的分类器,根据数据对其进行训练,瞧:您将获得96.2%的准确率!
你的老板很惊讶,决定使用你的模型,没有任何进一步的测试。几周后,他走进你的办公室,强调你的模型是无用的。事实上,您创建的模型从生产中使用以来就没有发现任何有缺陷的产品。
经过一些调查,您发现贵公司生产的产品中只有大约 3.8% 是有缺陷的,您的模型总是回答“没有缺陷”,导致 96.2% 的准确率。您获得的那种“幼稚”结果是由于您正在使用的不平衡数据集。本文的目的是回顾可用于解决不平衡类分类问题的不同方法。
大纲
首先,我们将概述有助于检测“幼稚行为”的不同评估指标。然后,我们将讨论包括重新设计数据集的一大堆方法,并表明这些方法可能会产生误导。最后,我们将证明,在大多数情况下,返工问题是最好的方法。
由(∞)符号表示的某些小节包含更多的数学细节,可以跳过而不会影响本文的整体理解。另请注意,在下面的大部分内容中,我们将考虑两个类分类问题,但推理可以很容易地扩展到多类情况。
二、检测“幼稚行为”
在第一节中,我们想提醒评估经过训练的分类器的不同方法,以确保检测到任何类型的“幼稚行为”。正如我们在引言的例子中看到的,准确性虽然是一个重要且不可避免的指标,但可能会产生误导,因此应谨慎使用并与其他指标一起使用。让我们看看可以使用哪些其他工具。
2.1 混淆矩阵、精度、召回率和 F1
在处理分类问题时应始终使用的一个良好而简单的指标是混淆矩阵。该指标提供了模型表现如何的有趣概述。因此,它是任何分类模型评估的一个很好的起点。我们在下图中总结了可以从混淆矩阵得出的大多数指标
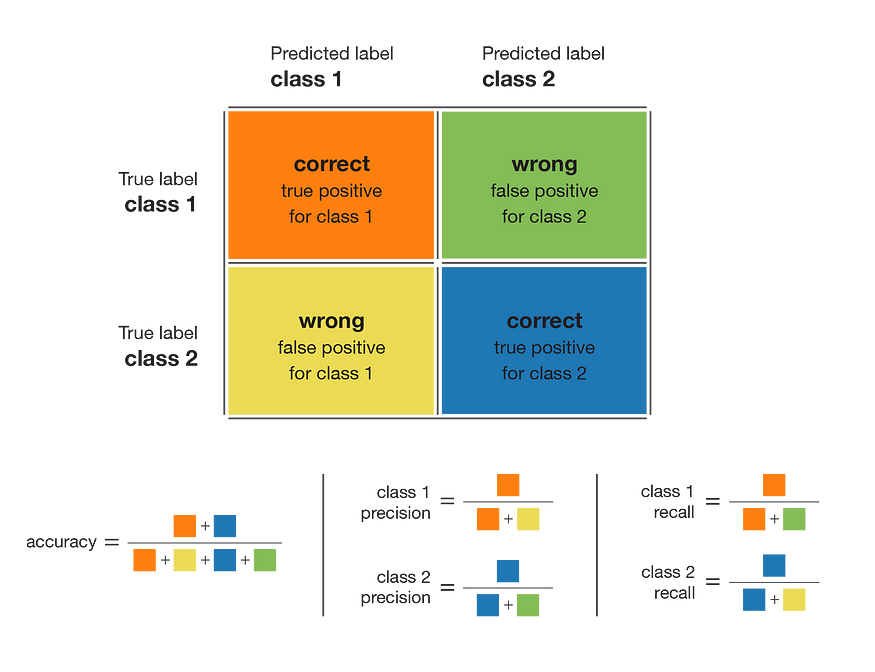
混淆矩阵和可以从中派生的指标。
让我们对这些指标进行简短描述。模型的准确性基本上是正确预测的总数除以预测总数。类的精度定义了当模型回答某个点属于该类时结果的可信度。类的召回表示模型能够检测到该类的程度。一个类的F1分数由精度和召回率的调和平均值(2×精度×召回率/(精度+召回率))给出,它将一个类的精度和召回率组合在一个指标中。
对于给定的类,召回率和精度的不同组合具有以下含义:
- 高召回率+高精度:模型完美处理类
- 低召回率+高精度:该模型不能很好地检测该类,但当它检测到时非常可信
- 高召回率+低精度:该类被很好地检测到,但模型中还包括其他类的点
- 低召回率+低精度:模型对类处理不当
在我们的介绍性示例中,我们有以下 10000 种产品的混淆矩阵。

我们介绍性示例的混淆矩阵。请注意,无法计算“有缺陷”的精度。
如前所述,准确率为96.2%。无缺陷类精度为96.2%,缺陷类精度不可计算。无缺陷类的召回率为1.0,这是完美的(所有无缺陷产品都已贴上标签)。但缺陷类的召回率为0.0,这是最糟糕的情况(未检测到有缺陷的产品)。因此,我们可以得出结论,我们的模型在此类中表现不佳。F1 分数对于有缺陷的产品不可计算,对于无缺陷产品为 0.981。在这个例子中,查看混淆矩阵可能会导致重新思考我们的模型或目标(我们将在以下各节中看到)。它本可以防止使用无用的模型。
中华民国和ROC
另一个有趣的指标是 ROC 曲线(代表接收器工作特性),它是针对给定类定义的(我们将在下面表示 C)。
假设对于给定的点 x,我们有一个模型,该模型输出该点属于 C 的概率:P(C | x)。基于这个概率,我们可以定义一个决策规则,包括当且仅当 P(C | x)≥T 时 x 属于类 C,其中 T 是定义我们决策规则的给定阈值。如果 T=1,则仅当模型具有 100% 置信度时,才会将点标记为属于 C。如果 T=0,则每个点都标记为属于 C。
阈值 T 的每个值都会生成一个点(假阳性、真阳性),然后,ROC 曲线是由 T 从 1 到 0 变化时生成的点集合描述的曲线。该曲线从点 (0,0) 开始,在点 (1,1) 结束,并且正在增加。一个好的模型将有一条从 0 快速增加到 1 的曲线(这意味着只需要牺牲一点精度即可获得高召回率)。
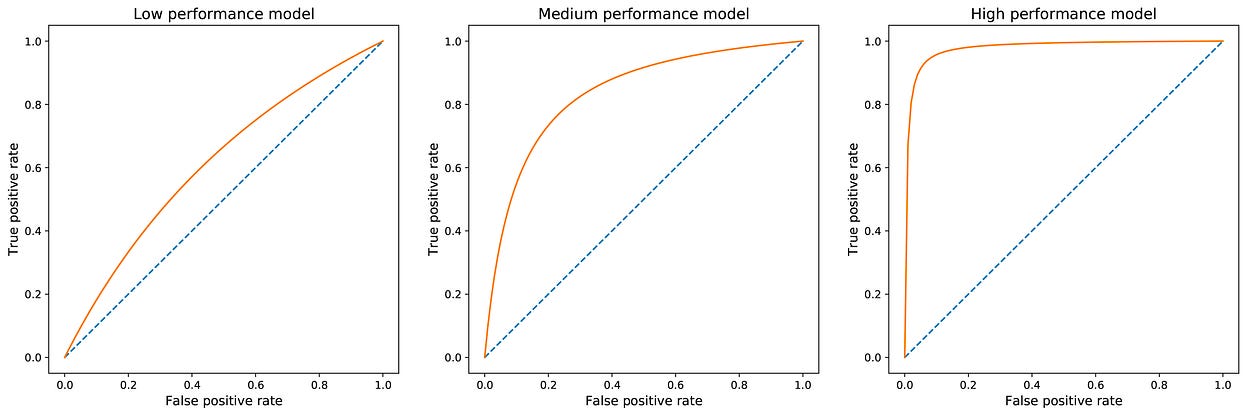
根据模型的有效性显示可能的 ROC 曲线。在左边,模型必须牺牲很多精度才能获得高召回率。在右侧,该模型非常有效:它可以在保持高精度的同时达到高召回率。
基于 ROC 曲线,我们可以构建另一个更易于使用的指标来评估模型:AUROC,即 ROC 曲线下的面积。AUROC 充当汇总整个 ROC 曲线的标量值。可以看出,AUROC 在最佳情况下趋向于 1.0,在最坏情况下趋向于 0.5。
同样,良好的AUROC分数意味着我们正在评估的模型不会牺牲很多精度来获得对观察到的类(通常是少数类)的良好召回。
三、问题到底出在哪里?
在尝试解决问题之前,让我们尝试更好地理解它。为此,我们将考虑一个非常简单的示例,该示例将使我们能够快速回顾两类分类的一些基本方面,并更好地掌握不平衡数据集的基本问题。此示例也将在以下各节中使用。
3.1 一个不平衡的例子
假设我们有两个类:C0 和 C1。类 C0 中的点服从均值 0 和方差 4 的一维高斯分布。类 C1 中的点遵循均值 2 和方差 1 的一维高斯分布。还假设在我们的问题中,类 C0 代表数据集的 90%(因此,类 C1 代表剩余的 10%)。在下图中,我们描绘了一个包含 50 个点的代表性数据集,以及两个类的理论分布,比例正确
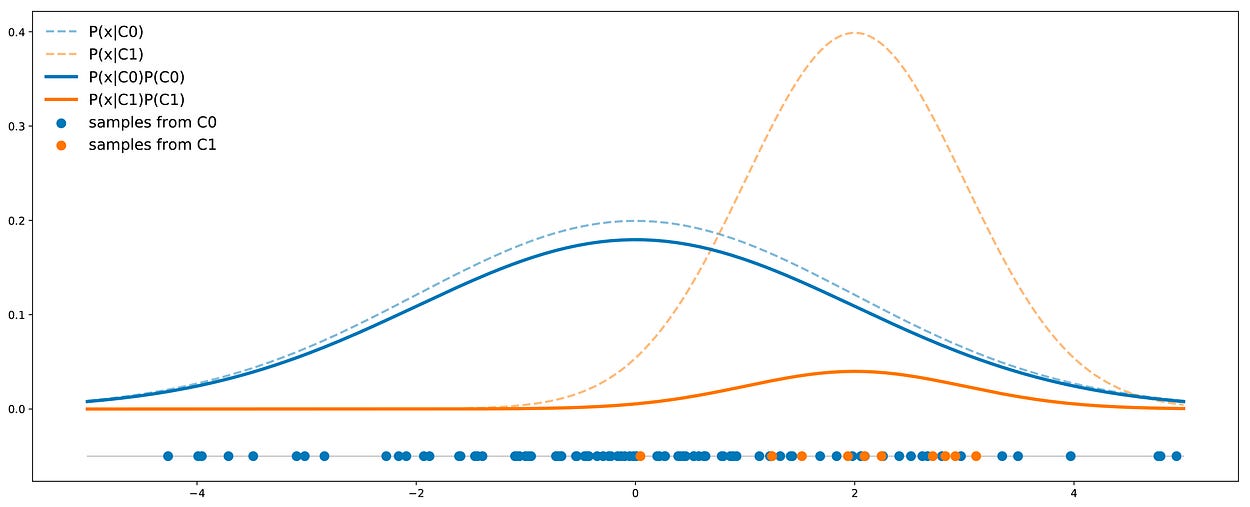
说明我们的不平衡示例。虚线独立表示每个类的概率密度。实线也考虑了比例。
在此示例中,我们可以看到 C0 类的曲线始终高于 C1 类的曲线,因此,对于任何给定点,该点从类 C0 绘制的概率始终大于从类 C1 绘制的概率。在数学上,使用基本的贝叶斯规则,我们可以写
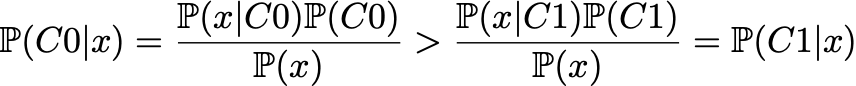
在这里,我们可以清楚地看到先验的影响,以及它如何导致一个类总是比另一个类更有可能的情况。
所有这些都意味着,即使从完美的理论角度来看,我们也知道,如果我们必须在这些数据上训练分类器,那么当始终回答 C0 时,分类器的准确性将是最大的。因此,如果目标是训练分类器以获得最佳的准确性,那么它不应该被视为一个问题,而应该被视为一个事实:有了这些功能,我们能做的最好的事情(就准确性而言)就是始终回答 C0。我们必须接受它。
3.2 关于可分离性
在给定的示例中,我们可以观察到这两个类不能很好地分离(它们彼此相距不远)。但是,我们可以注意到,面对不平衡的数据集并不一定意味着这两个类不能很好地分离,因此,分类器不能很好地处理少数类。例如,假设我们仍然有两个类 C0 (90%) 和 C1 (10%)。C0 中的数据服从均值 0 和方差 4 的一维高斯分布,而 C1 中的数据服从均值 10 和方差 1 的一维高斯分布。如果我们像以前一样绘制数据,那么我们就有
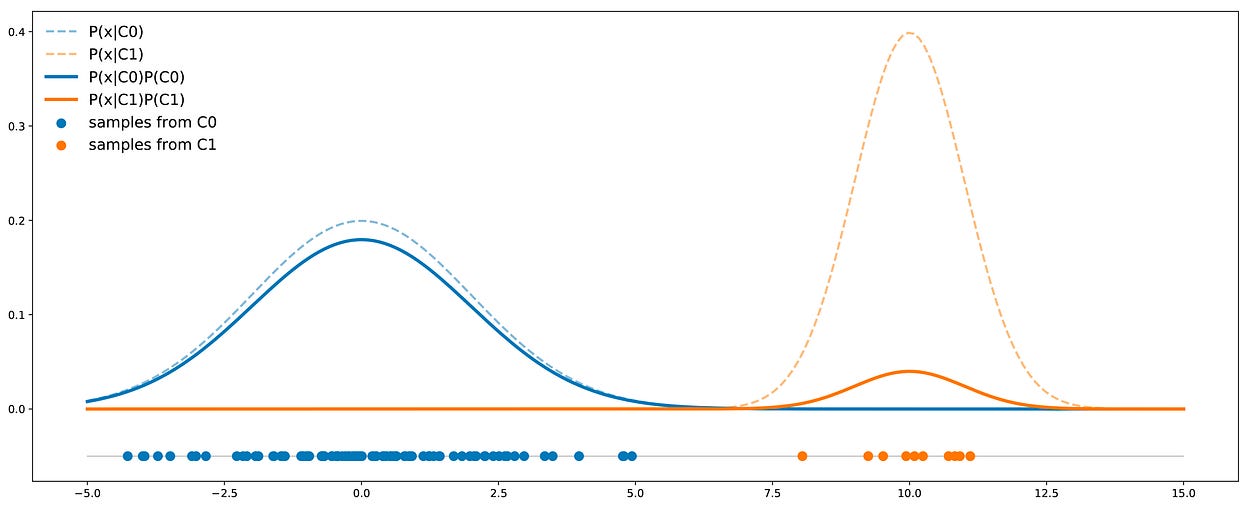
在我们的高斯示例中,如果均值相对于方差足够不同,即使是不平衡的类也可以很好地分离。
在这里,我们看到与前一种情况相反,C0 曲线并不总是高于 C1 曲线,因此,有些点更有可能从类 C1 而不是从类 C0 中提取。在这种情况下,这两个类的分离足以补偿不平衡:分类器不一定总是回答 C0。
3.3 理论最小误差概率(∞)
最后,我们应该记住,分类器具有理论上的最小误差概率。对于这种分类器(一个特征,两个类),我们可以提到,以图形方式,理论最小误差概率由两条曲线的最小值下的面积给出。

两类不同可分离程度的理论最小误差图示。
我们可以在数学上恢复这种直觉。事实上,从理论的角度来看,最好的分类器将为每个点x选择两个类中最有可能的。这自然意味着,对于给定的点x,最佳理论误差概率由这两个类中可能性较小的给出
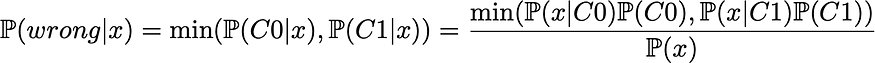
然后我们可以表示整体错误概率
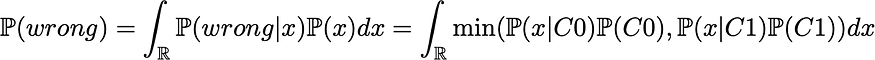
这是上面表示的两条曲线的最小值下的面积。
四、返工数据集并不总是解决方案
首先,面对不平衡的数据集时,第一个可能的反应是考虑数据不能代表现实:如果是这样,我们假设真实数据几乎是平衡的,但在收集的数据中存在比例偏差(例如,由于收集方法)。在这种情况下,几乎必须尝试收集更具代表性的数据。
现在让我们看看,当数据集不平衡时可以做什么,因为现实就是如此。在接下来的两个小节中,我们将介绍一些经常提到的方法,这些方法用于处理不平衡的类以及处理数据集本身的方法。特别是,我们讨论了与欠采样、过采样和生成合成数据相关的风险,以及获得更多功能的好处。
4.1 欠采样、过采样和生成合成数据
这些方法通常被认为是在拟合分类器之前平衡数据集的好方法。简而言之,这些方法作用于数据集,如下所示:
- 欠采样包括从多数类中抽样,以便仅保留这些点的一部分
- 过采样包括从少数类复制一些点以增加其基数
- 生成合成数据包括从少数类创建新的合成点(例如,请参阅 SMOTE 方法)以增加其基数
所有这些方法都旨在重新平衡(部分或全部)数据集。但是我们应该重新平衡数据集以拥有两个类的尽可能多的数据吗?还是应该让多数阶级保持最具代表性?如果是这样,我们应该以什么比例重新平衡?
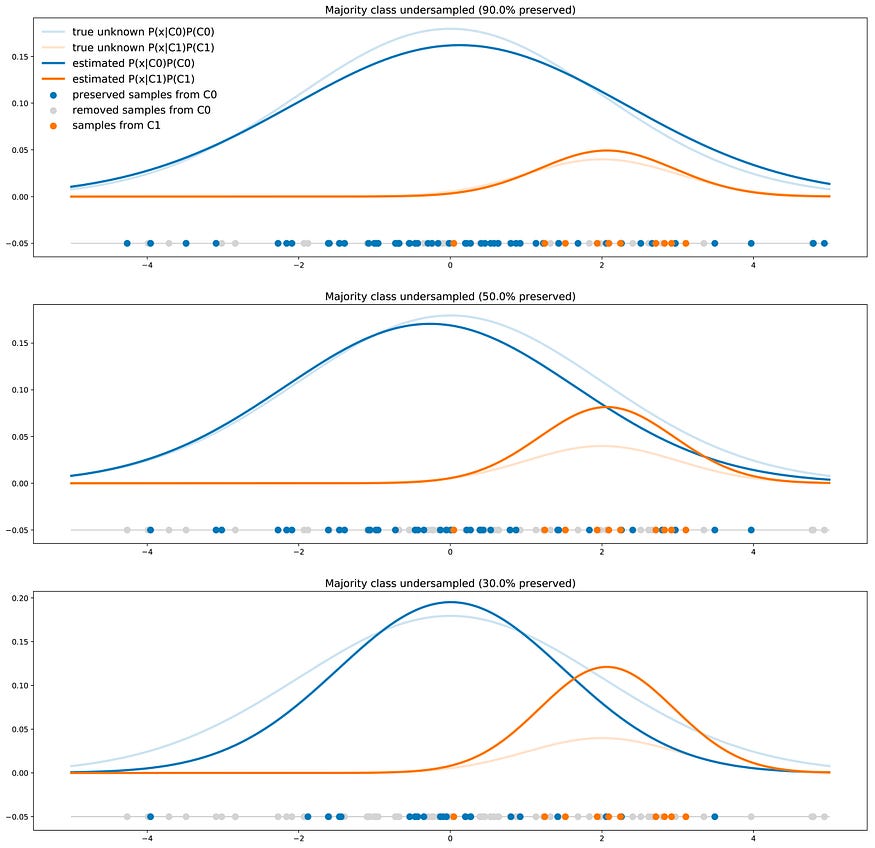
说明不同程度的多数类欠采样对模型决策的影响。
当使用重采样方法时(例如,从 C0 获取的数据与从 C1 获取的数据一样多),我们在训练期间向分类器显示两个类的错误比例。这样学习的分类器对未来真实测试数据的准确率将低于在未更改数据集上训练的分类器。事实上,了解类的真实比例对于对新点进行分类非常重要,并且在对数据集进行重采样时,该信息已丢失。
因此,如果这些方法不必被完全拒绝,则应谨慎使用:如果有目的地选择新的比例,它可能会导致相关的方法(我们将在下一节中看到),但只是重新平衡类而不进一步考虑问题也可能是无稽之谈。为了结束本小节,假设使用类似重采样的方法修改数据集正在改变现实,因此需要小心并牢记它对分类器的输出结果意味着什么。
4.2 获取其他功能
我们在上一小节中讨论了这样一个事实,即根据分类器的真正目的,对训练数据集进行重采样(修改类比例)可能是也可能不是一个好主意。我们特别看到,如果两个类不平衡,不能很好地分离,并且我们以尽可能高的精度定位分类器,那么获得一个总是回答相同类的分类器不一定是一个问题,而只是一个事实:没有什么比这些变量更好的了。
但是,通过使用附加(或更多)特征丰富数据集,仍然可以在准确性方面获得更好的结果。让我们回到类不能很好地分离的第一个示例:也许我们可以找到一个新的附加功能来帮助区分两个类,从而提高分类器的准确性。
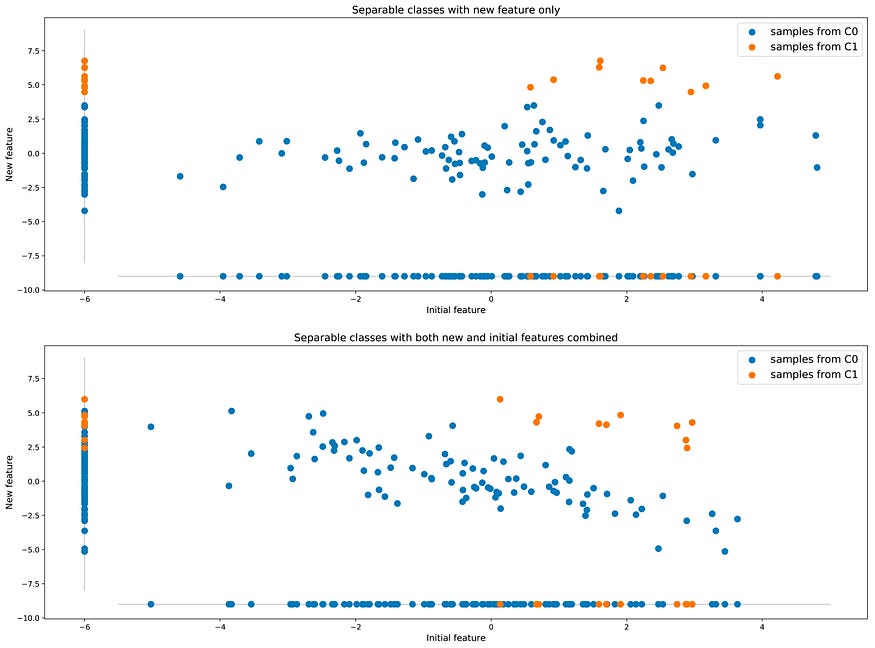
寻找其他功能可以帮助分离最初不可分离的两个类。
与上一小节中提到的建议改变数据现实的方法相比,这种包括用来自现实的更多信息丰富数据的方法在可能的情况下是一个更好的主意。
五、返工问题更好
到目前为止,结论非常令人失望:如果数据集代表真实数据,如果我们无法获得任何附加特征,并且如果我们以最佳的准确性定位分类器,那么“幼稚行为”(总是回答相同的类)不一定是问题,应该被接受为事实(如果幼稚行为不是由于所选分类器的能力有限, 当然)。
那么,如果我们仍然对这些结果不满意怎么办?在这种情况下,这意味着,以一种或另一种方式,我们的问题没有得到很好的陈述(否则我们应该接受结果的本来面目),我们应该重新设计它以获得更令人满意的结果。让我们看一个例子。
5.1 基于成本的分类
获得的结果不好的感觉可能来自目标函数没有很好地定义的事实。到目前为止,我们假设我们以高精度定位分类器,同时假设两种错误(“假阳性”和“假阴性”)具有相同的成本。在我们的示例中,这意味着我们假设当真实标签为 C0 时预测 C1 与在真实标签为 C1 时预测 C0 一样糟糕。然后错误是对称的。
让我们考虑有缺陷的 (C1) 和没有缺陷的 (C0) 产品的介绍性示例。在这种情况下,我们可以想象,不检测到有缺陷的产品会给公司带来更多的成本(客户服务成本,如果存在危险缺陷,则可能的法律成本,...)比错误地将没有缺陷的产品标记为有缺陷(生产成本损失)。现在,当真标签为 C0 时预测 C1 比在真标签为 C1 时预测 C0 要差得多。错误不再是对称的。
然后更具体地考虑我们有以下成本:
- 当真实标签为 C0 时预测 C1 的成本为 P01
- 当真实标签为 C1 时预测 C0 的成本为 P10(0 < P10 << P01)
然后,我们可以重新定义我们的目标函数:我们不再以最佳准确性为目标,而是寻找较低的预测成本。
5.2 理论最小成本 (∞)
从理论角度来看,我们不想最小化上面定义的误差概率,而是最小化由

其中 C(.) 定义分类器函数。因此,如果我们想最小化预期的预测成本,理论上的最佳分类器 C(.) 最小化
![]()
或等价地,除以 x,C(.) 的密度最小化
![]()
因此,有了这个目标函数,从理论角度来看,最好的分类器将是这样的:

请注意,当成本相等时,我们恢复“经典”分类器的表达式(专注于准确性)。
5.3 概率阈值
在我们的分类器中考虑成本的第一个可能方法是在训练后进行。这个想法是,首先,训练分类器输出以下概率的基本方法
![]()
无需承担任何费用。然后,预测的类将为 C0,如果
![]()
否则为 C1。
在这里,我们使用哪个分类器并不重要,只要它输出给定点的每个类的概率即可。在我们的主示例中,我们可以在数据上拟合贝叶斯分类器,然后我们可以重新加权获得的概率,以使用描述的成本误差调整分类器。
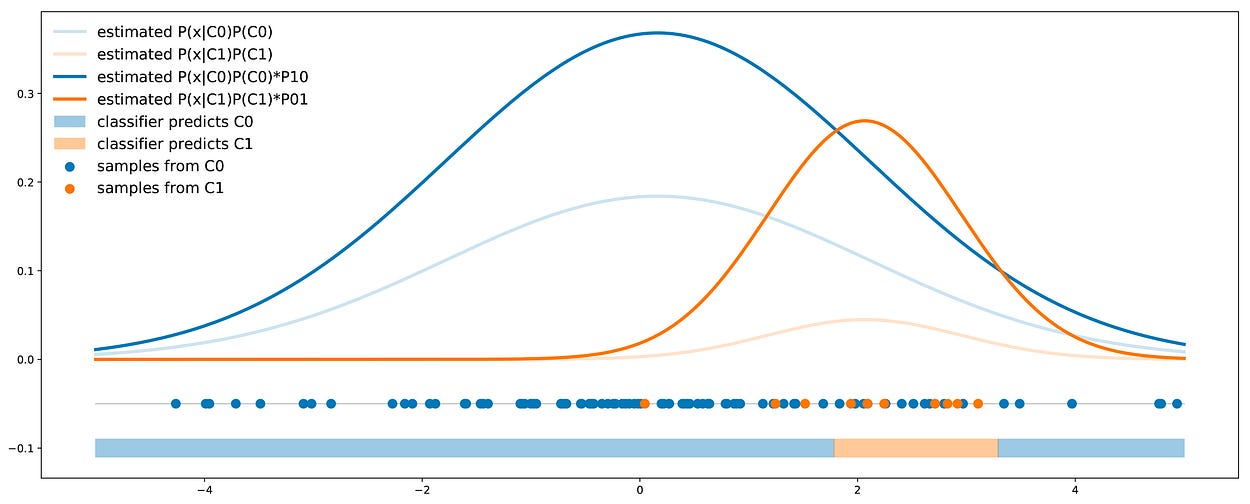
概率阈值方法的图示:对输出的概率进行重新加权,以便在最终决策规则中考虑成本。
5.4 类重新加权
类重新加权的想法是在分类器训练期间直接考虑成本误差的不对称性。这样,每个类的输出概率已经嵌入了成本错误信息,然后可用于定义具有简单 0.5 阈值的分类规则。
对于某些模型(例如神经网络分类器),在训练期间考虑成本可能包括调整目标函数。我们仍然希望我们的分类器输出
![]()
但这次它经过训练,以最小化以下成本函数
![]()
对于其他一些模型(例如贝叶斯分类器),重采样方法可用于偏置类比例,以便在类比例内输入成本误差信息。如果我们考虑成本 P01 和 P10(例如 P01 > P10),我们可以:
- 将少数类过采样因子 P01/P10(少数类的基数应乘以 P01/P10)
- 多数类的欠采样系数 P10/P01(多数类的基数应乘以 P10/P01)
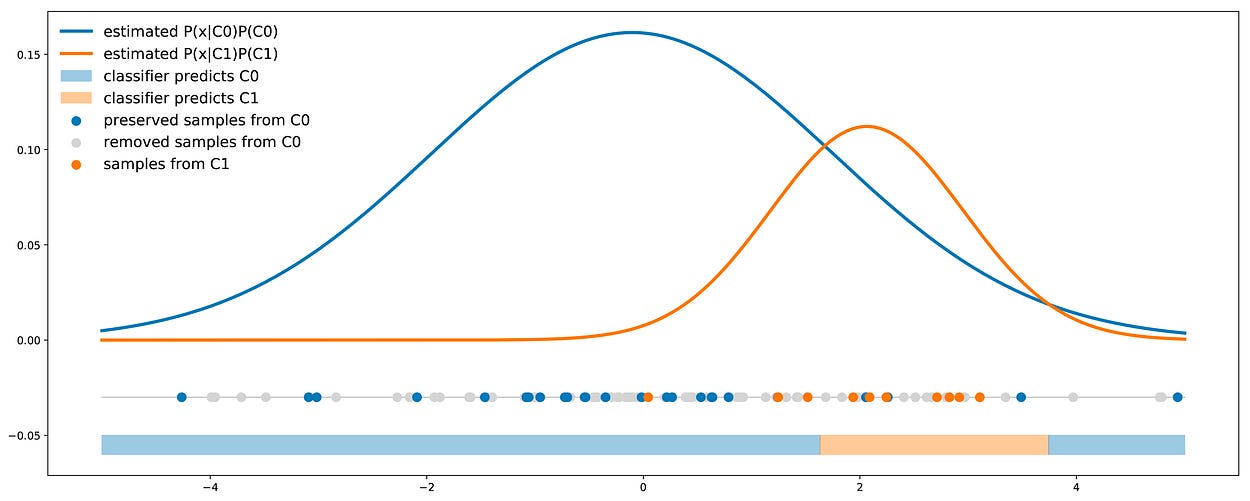
类加权法的图示:多数类的抽样不足,其比例经过精心选择,以直接在类比例内引入成本信息。
六、总结
本文的主要内容是:
- 每当使用机器学习算法时,都必须谨慎选择模型的评估指标:我们必须使用能够让我们最好地了解模型在目标方面做得如何的指标。
- 在处理不平衡的数据集时,如果类不能与给定变量很好地分离,并且我们的目标是获得最佳的准确性,则最佳分类器可以是始终回答多数类的“幼稚”分类器
- 可以使用重采样方法,但必须仔细考虑:它们不应用作独立的解决方案,而必须与问题的返工相结合以服务于特定目标
- 重新设计问题本身通常是解决不平衡类问题的最佳方法:分类器和决策规则必须针对一个精心选择的目标进行设置,例如,可以最小化成本
我们应该注意到,我们还没有讨论过像“分层采样”这样的技术,这些技术在批量训练分类器时很有用。当遇到不平衡类问题时,这些技术可确保在训练过程中提高稳定性(通过消除批次内的比例方差)。
最后,假设本文的主要关键字是“目标”。确切地知道您想要获得的内容将有助于克服不平衡的数据集问题,并确保获得最佳结果。完美地定义目标应该始终是第一件事,并且是创建机器学习模型所必须进行的任何选择的起点。巴蒂斯特·罗卡
相关文章:

【机器学习】处理不平衡的数据集
一、介绍 假设您在一家给定的公司工作,并要求您创建一个模型,该模型根据您可以使用的各种测量来预测产品是否有缺陷。您决定使用自己喜欢的分类器,根据数据对其进行训练,瞧:您将获得96.2%的准确率! …...
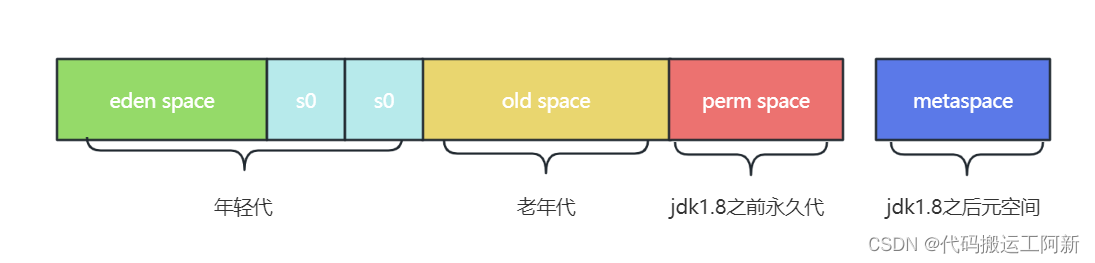
JVM前世今生之JVM内存模型
JVM内存模型所指的是JVM运行时区域,该区域分为两大块 线程共享区域 堆内存、方法区,即所有线程都能访问该区域,随着虚拟机和GC创建和销毁 线程独占区域 虚拟机栈、本地方法栈、程序计数器,即每个线程都有自己独立的区域&#…...

redis事务对比Lua脚本区别是什么
redis官方对于lua脚本的解释:Redis使用同一个Lua解释器来执行所有命令,同时,Redis保证以一种原子性的方式来执行脚本:当lua脚本在执行的时候,不会有其他脚本和命令同时执行,这种语义类似于 MULTI/EXEC。从别…...

Java“牵手”根据店铺ID获取1688店铺所有商品数据方法,1688API实现批量店铺商品数据抓取示例
1688商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取1688整店所有商品详情页面评价内容数据,您可以通过开放平台的接口或者直接访问1688商城的网页来获取店铺所有商品详情信息的数据。以下是两…...

linux-shell脚本收集
创建同步脚本xsync mkdir -p /home/hadoop/bin && cd /home/hadoop/bin vim xsync#!/bin/bash#1. 判断参数个数 if [ $# -lt 1 ] thenecho Not Arguementexit; fi#2. 遍历集群所有机器 for host in node1 node2 node3 doecho $host #3. 遍历所有目录,挨…...

使用 MBean 和 日志查看 Tomcat 线程池核心属性数据
文章目录 CustomTomcatThreadPoolMBeanCustomTomcatThreadPool CustomTomcatThreadPoolMBean com.qww.config;public interface CustomTomcatThreadPoolMBean {String getStatus(); }CustomTomcatThreadPool package com.qww.config;import com.alibaba.fastjson.JSON; impor…...
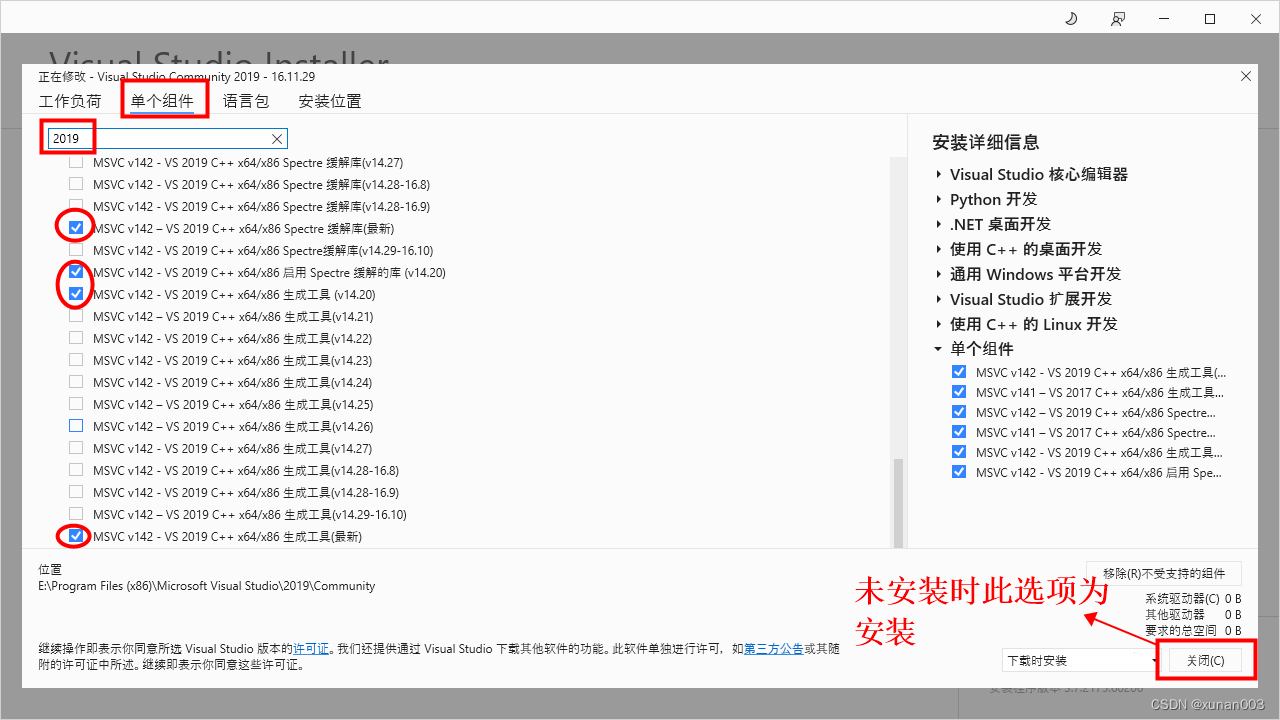
Visual Studio 2019源码编译cpu版本onnxruntime
1.下载onnxruntime源码 源码地址:gitee 》https://gitee.com/mirrors/onnx-runtime github 》https://github.com/microsoft/onnxruntime git clone --recursive https://gitee.com/mirrors/onnx-runtime 2.安装anaconda并配置python环境 安装anaconda时记得勾选默…...

Go和Java实现模板模式
Go和Java实现模板模式 下面通过一个游戏的例子来说明模板模式的使用。 1、模板模式 在模板模式中,一个抽象类公开定义了执行它的方法的方式/模板。它的子类可以按需要重写方法实现,但调用将 以抽象类中定义的方式进行。这种类型的设计模式属于行为型…...

angular:quill align的坑
上一行设置了align为center,换行后下一个会继承上一行的格式,我想使用Quill.formatLine(newLineIndex, 0, ‘align’, left)来左对齐,发现始终不能生效。 参看quill.js源码,发现align没有left的配置 var config {scope: _parch…...
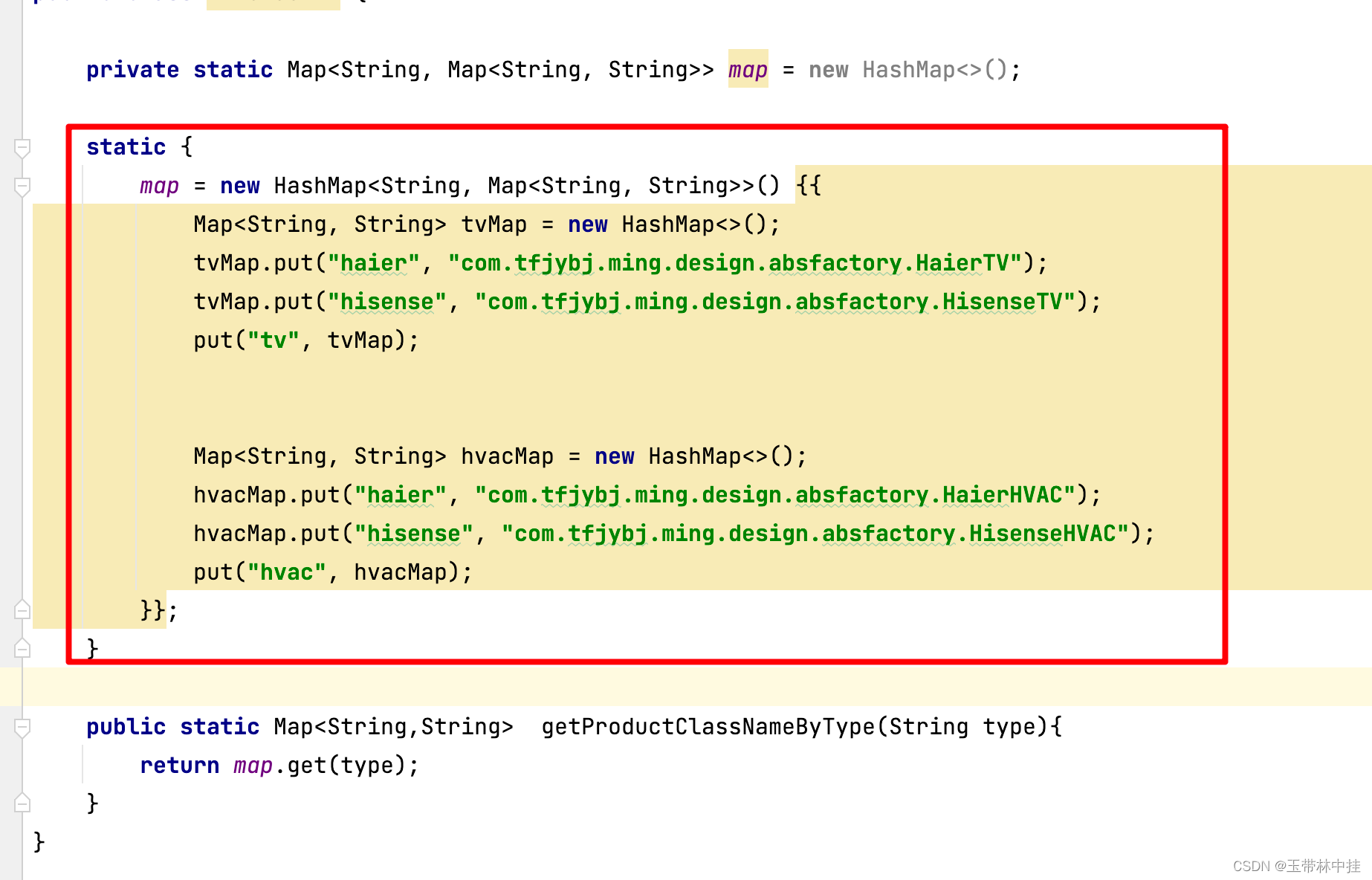
设计模式篇---抽象工厂(包含优化)
文章目录 概念结构实例优化 概念 抽象工厂:提供一个创建一系列相关或相互依赖对象的接口,而无须指定它们具体的类。 工厂方法是有一个类型的产品,也就是只有一个产品的抽象类或接口,而抽象工厂相对于工厂方法来说,是有…...
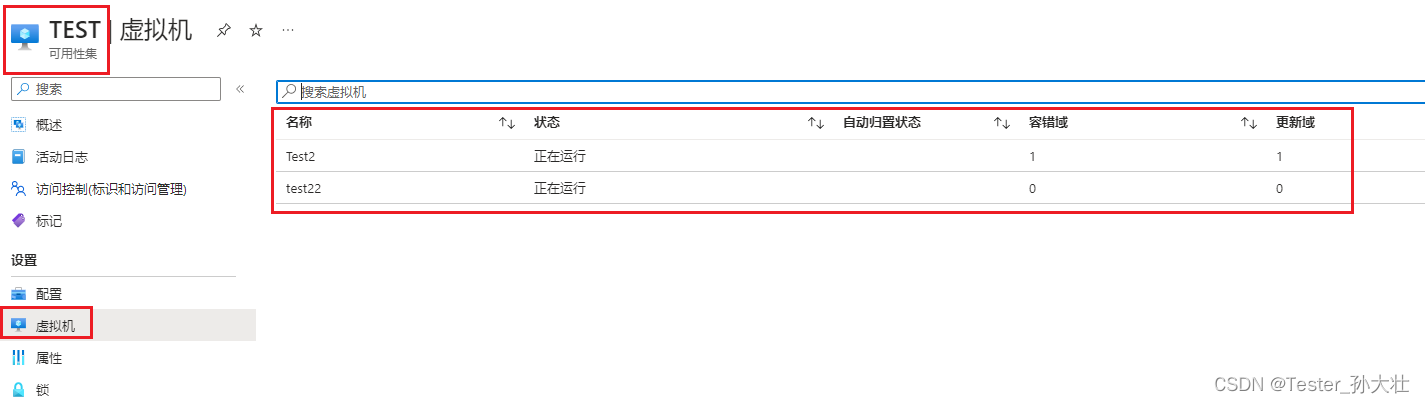
Azure创建可用性集
什么是可用性集 在Azure中,可用性集(Availability Set)是一种用于提高虚拟机(VM)可用性和可靠性的功能。它通过将虚拟机分布在不同的物理硬件和故障域中来提供高可用性。每个故障域都是一个独立的电力和网络故障区域&…...

SpringBoot中优雅的实现隐私数据脱敏(提供Gitee源码)
前言:在实际项目开发中,可能会对一些用户的隐私信息进行脱敏操作,传统的方式很多都是用replace方法进行手动替换,这样会由很多冗余的代码并且后续也不好维护,本期就讲解一下如何在SpringBoot中优雅的通过序列化的方式去…...

Elasticsearch集群shard过多后导致的性能问题分析
1.问题现象 上午上班以后发现ES日志集群状态不正确,集群频繁地重新发起选主操作。对外不能正常提供数据查询服务,相关日志数据入库也产生较大延时 2.问题原因 相关日志 查看ES集群日志如下: 00:00:51开始集群各个节点与当时的master节点…...
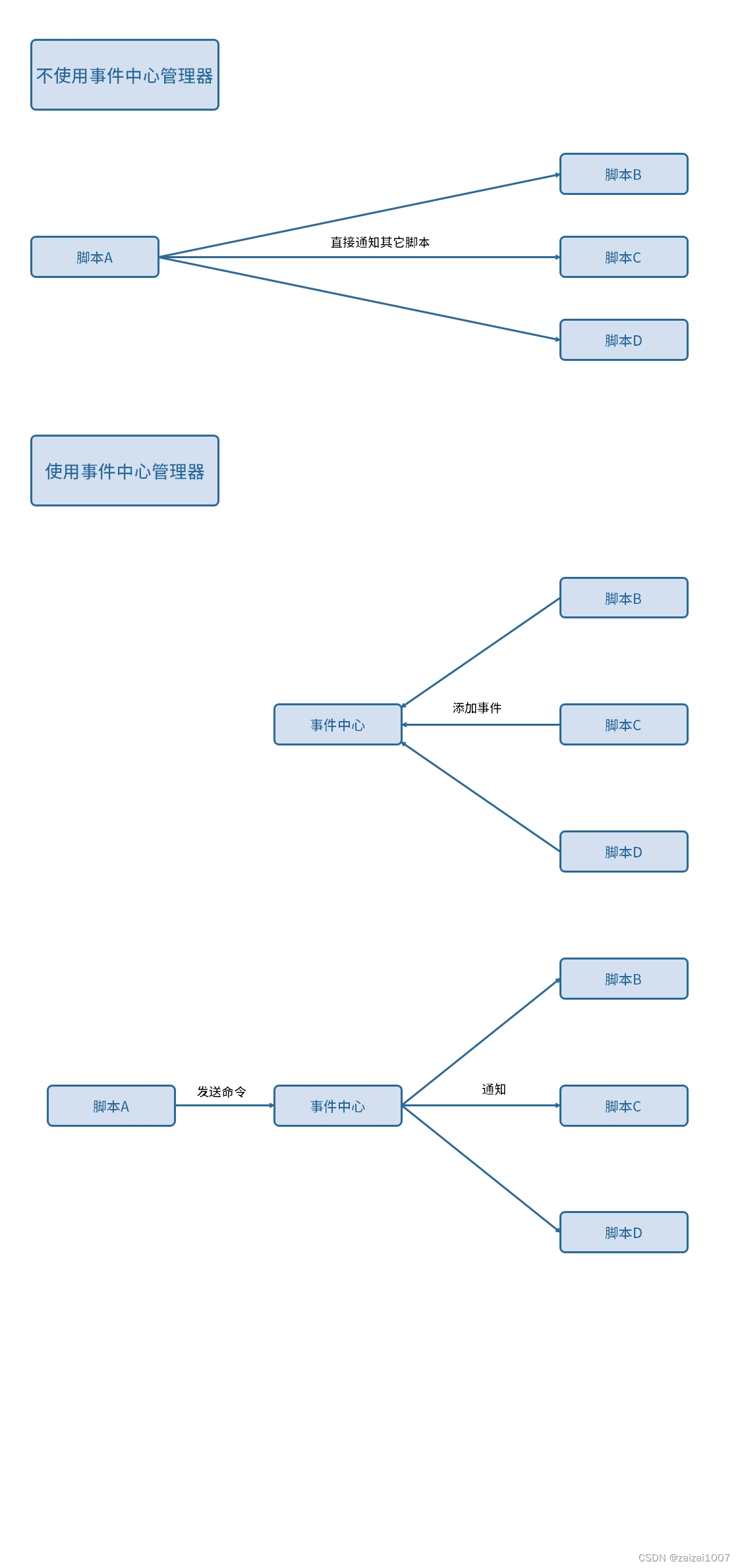
Unity框架学习--5 事件中心管理器
作用:访问其它脚本时,不直接访问,而是通过发送一条“命令”,让监听了这条“命令”的脚本自动执行对应的逻辑。 原理: 1、让脚本向事件中心添加事件,监听对应的“命令”。 2、发送“命令”,事件…...
结构型模式:3、过滤器模式(Filter、Criteria Pattern)(C++示例))
(二)结构型模式:3、过滤器模式(Filter、Criteria Pattern)(C++示例)
目录 1、过滤器模式(Filter、Criteria Pattern)含义 2、过滤器模式应用场景 3、过滤器模式主要几个关键角色 4、C实现过滤器模式的示例 1、过滤器模式(Filter、Criteria Pattern)含义 (1)过滤器模式是…...
谷歌在Chrome浏览器中推进抗量子加密技术
近日,Chromium博客上发表的一篇博文称,为了加强网络安全,应对迫在眉睫的量子计算机威胁,谷歌各个团队密切合作,为网络向抗量子密码学的过渡做好准备。 谷歌的Chrome团队在博客中写道,该项目涉及修订技术标准…...

Kotlin的数组
在 Kotlin 中,数组是一种固定大小的有序集合,可以存储相同类型的元素。Kotlin 提供了两种类型的数组:原生数组和数组类。以下是 Kotlin 中数组的详细使用方法: 1.创建数组 Kotlin 支持使用 arrayOf() 函数来创建数组:…...

centos 安装docker
1.更新你的系统: sudo yum update -y2.安装必需的软件包: Docker 需要 yum-utils, device-mapper-persistent-data 和 lvm2 软件包来运行。安装它们: sudo yum install -y yum-utils device-mapper-persistent-data lvm23.设置 Docker 的仓库: 使用以下命令添加 D…...
Oracle-如何判断字符串包含中文字符串(汉字),删除中文内容及保留中文内容
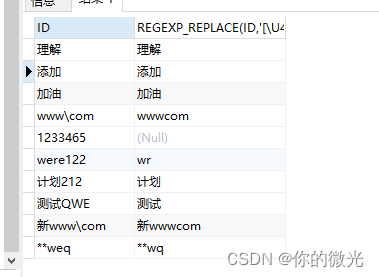
今天遇见一个问题需要将字段中包含中文字符串的筛选出来 --建表 CREATE TABLE HADOOP1.AAA ( ID VARCHAR2(255) ); --添加字段INSERT INTO HADOOP1.AAA(ID)VALUES(理解);....--查询表内容SELECT * FROM HADOOP1.AAA;在网上查找了一下有以下三种方式: 第一种&#…...
File 类的用法, InputStream和Reader, OutputStream和Writer 的用法
前言 普通的文件长这样: 其实目录也是一种特殊文件: 一、文件前缀知识 (一)绝对路径和相对路径 以盘符开头的的路径,叫做绝对路径,如:D:\360Downloads\cat.jpg 以.或..开头的路径,…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
