Azure创建可用性集
什么是可用性集
在Azure中，可用性集（Availability Set）是一种用于提高虚拟机（VM）可用性和可靠性的功能。它通过将虚拟机分布在不同的物理硬件和故障域中来提供高可用性。每个故障域都是一个独立的电力和网络故障区域，这意味着当一个故障域发生故障时，其他故障域中的虚拟机仍然可用。
可用性集确保您的虚拟机在维护、更新或硬件故障等情况下保持可用。Azure会确保您的虚拟机在可用性集中最多跨两个故障域分布，从而提高应用程序的可用性。
使用可用性集还可以创建虚拟机规模集（Virtual Machine Scale Sets），帮助您自动调整虚拟机的数量以满足应用程序的需求，并提供高可用性。
实战演练
- 创建可用性集
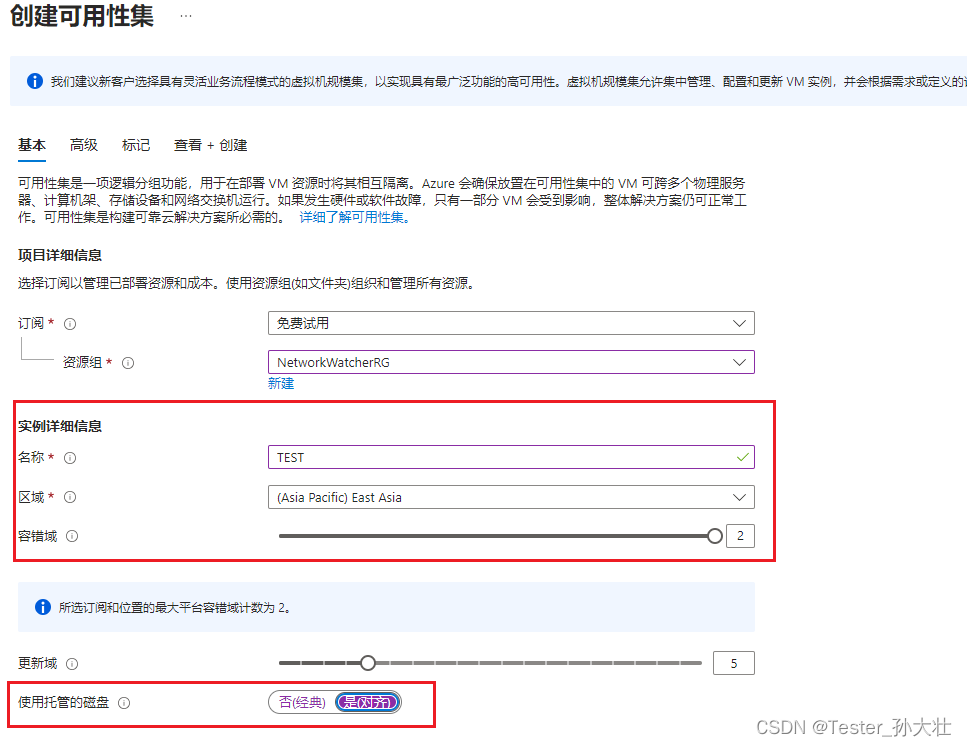
- 创建2个虚拟机，参考：https://editor.csdn.net/md/?articleId=132267096, 注意可用性集选择如上创建的可用性集
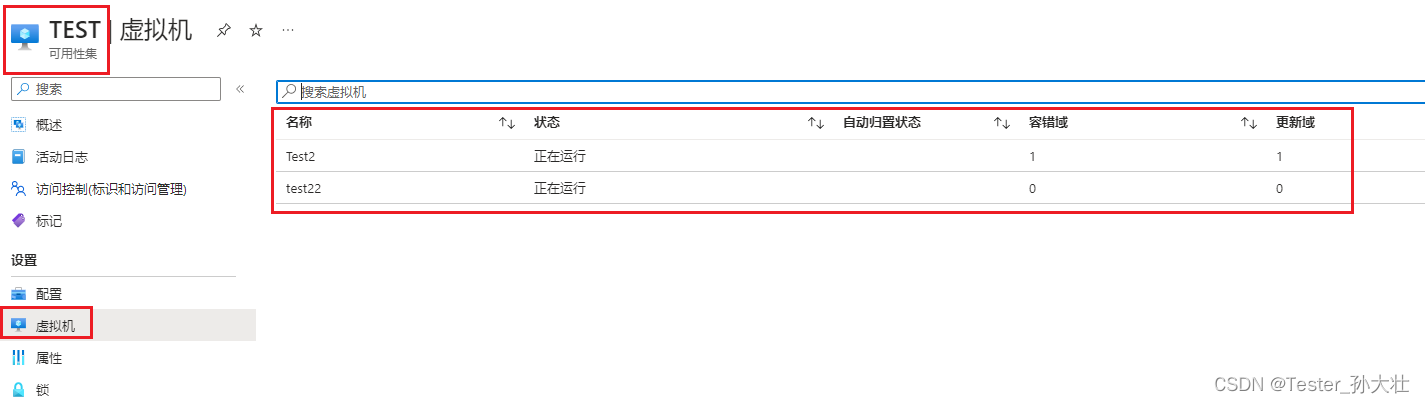
- 去可用性集中查看，此时可用性集合中部署了两个虚拟机
参考资料：
https://learn.microsoft.com/zh-cn/azure/virtual-machines/availability-set-overview
相关文章：
Azure创建可用性集
什么是可用性集 在Azure中，可用性集（Availability Set）是一种用于提高虚拟机（VM）可用性和可靠性的功能。它通过将虚拟机分布在不同的物理硬件和故障域中来提供高可用性。每个故障域都是一个独立的电力和网络故障区域&…...
SpringBoot中优雅的实现隐私数据脱敏（提供Gitee源码）
前言：在实际项目开发中，可能会对一些用户的隐私信息进行脱敏操作，传统的方式很多都是用replace方法进行手动替换，这样会由很多冗余的代码并且后续也不好维护，本期就讲解一下如何在SpringBoot中优雅的通过序列化的方式去…...
Elasticsearch集群shard过多后导致的性能问题分析
1.问题现象 上午上班以后发现ES日志集群状态不正确，集群频繁地重新发起选主操作。对外不能正常提供数据查询服务，相关日志数据入库也产生较大延时 2.问题原因 相关日志 查看ES集群日志如下： 00:00:51开始集群各个节点与当时的master节点…...
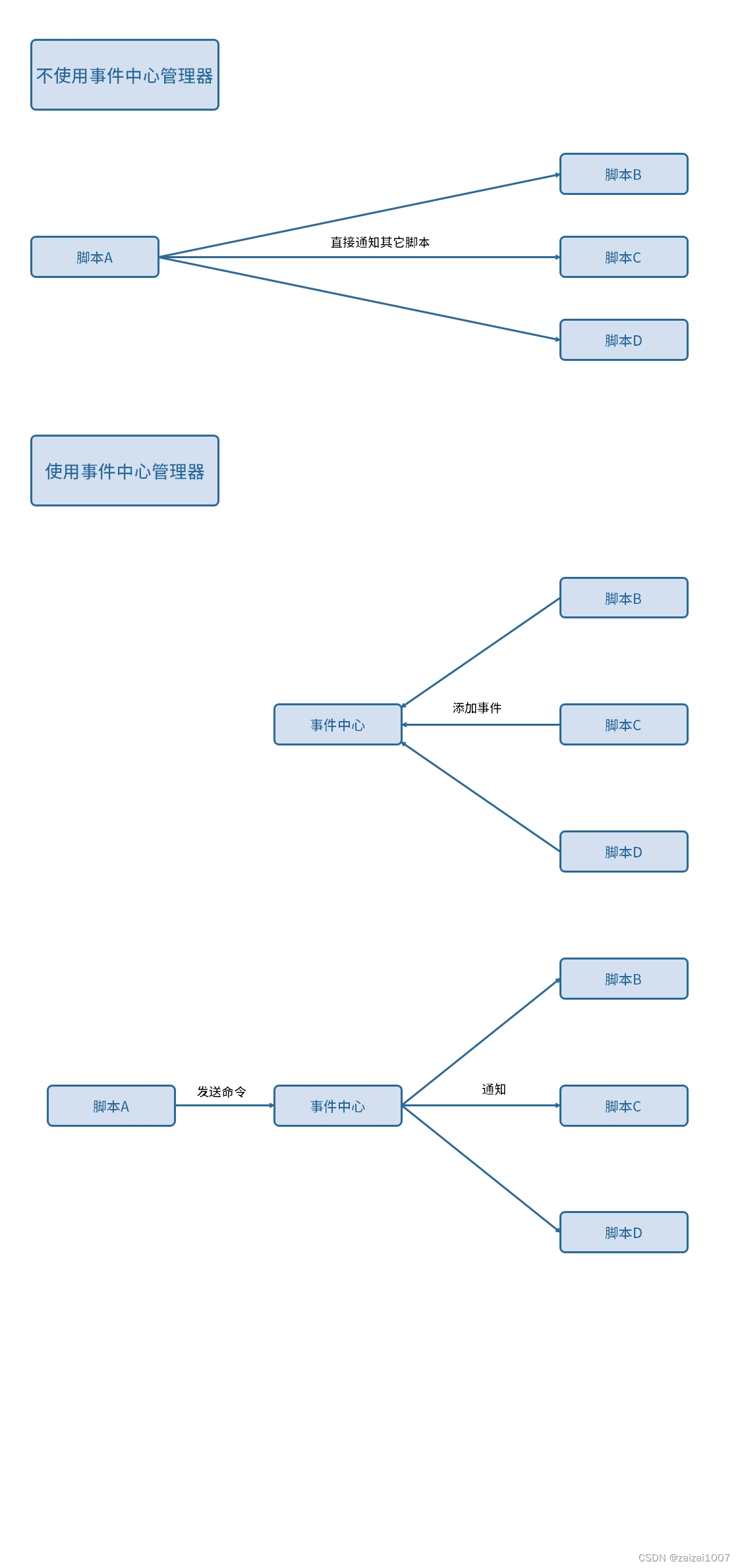
Unity框架学习--5 事件中心管理器
作用：访问其它脚本时，不直接访问，而是通过发送一条“命令”，让监听了这条“命令”的脚本自动执行对应的逻辑。 原理： 1、让脚本向事件中心添加事件，监听对应的“命令”。 2、发送“命令”，事件…...
（二）结构型模式：3、过滤器模式（Filter、Criteria Pattern）（C++示例）
目录 1、过滤器模式（Filter、Criteria Pattern）含义 2、过滤器模式应用场景 3、过滤器模式主要几个关键角色 4、C实现过滤器模式的示例 1、过滤器模式（Filter、Criteria Pattern）含义 （1）过滤器模式是…...
谷歌在Chrome浏览器中推进抗量子加密技术
近日，Chromium博客上发表的一篇博文称，为了加强网络安全，应对迫在眉睫的量子计算机威胁，谷歌各个团队密切合作，为网络向抗量子密码学的过渡做好准备。 谷歌的Chrome团队在博客中写道，该项目涉及修订技术标准…...
Kotlin的数组
在 Kotlin 中，数组是一种固定大小的有序集合，可以存储相同类型的元素。Kotlin 提供了两种类型的数组：原生数组和数组类。以下是 Kotlin 中数组的详细使用方法： 1.创建数组 Kotlin 支持使用 arrayOf() 函数来创建数组：…...
centos 安装docker
1.更新你的系统: sudo yum update -y2.安装必需的软件包: Docker 需要 yum-utils, device-mapper-persistent-data 和 lvm2 软件包来运行。安装它们： sudo yum install -y yum-utils device-mapper-persistent-data lvm23.设置 Docker 的仓库: 使用以下命令添加 D…...
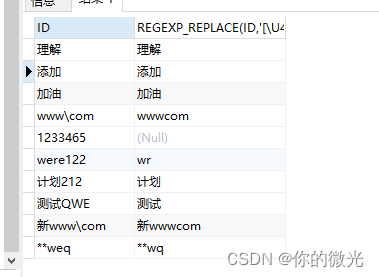
Oracle-如何判断字符串包含中文字符串（汉字），删除中文内容及保留中文内容
今天遇见一个问题需要将字段中包含中文字符串的筛选出来 --建表 CREATE TABLE HADOOP1.AAA ( ID VARCHAR2(255) ); --添加字段INSERT INTO HADOOP1.AAA(ID)VALUES(理解);....--查询表内容SELECT * FROM HADOOP1.AAA;在网上查找了一下有以下三种方式： 第一种&#…...
File 类的用法, InputStream和Reader, OutputStream和Writer 的用法
前言 普通的文件长这样： 其实目录也是一种特殊文件： 一、文件前缀知识 （一）绝对路径和相对路径 以盘符开头的的路径，叫做绝对路径，如：D:\360Downloads\cat.jpg 以.或..开头的路径，…...
AtCoder Beginner Contest 315 Task:A/B/C/E
A - tcdr 处理字符串简单题，题目要求去除字符串中的a,e,i,o,u即可 #include<iostream> using namespace std; int main() {string s;cin>>s;for(int i0;i<s.length();i){if(s[i]a||s[i]e||s[i]i||s[i]o||s[i]u)continue;cout<<s[i];} }B - T…...
【项目实践】基于LSTM的一维数据扩展与预测
基于LSTM的一维数据拟合扩展 一、引(fei)言(hua) 我在做Sri Lanka生态系统服务价值计算时，中间遇到了一点小问题。从世界粮农组织(FAO)上获得Sri Lanka主要农作物产量和价格数据时，其中的主要作物Sorghum仅有2001-2006年的数据，而Millet只有…...
webshell实践，在nginx上实现负载均衡
1、配置多台虚拟机，用作服务器 在不同的虚拟机上安装httpd服务 我采用了三台虚拟机进行服务器设置：192.168.240.11、192.168.240.12、192.168.240.13 [rootnode0-8 /]# yum install httpd -y #使用yum安装httpd服务#开启httpd服务 [rootnode0-8 /]# …...
LVS+Keepalived集群
keepalived Keepalived及其工作原理 Keepalived 是一个基于VRRP协议来实现的LVS服务高可用方案，可以解决静态路由出现的单点故障问题 在一个LVS服务集群中通常有主服务器（MASTER）和备份服务器（BACKUP）两种角色的服务…...
Java的网络编程
网络编程 两台设备之间通过网络实现数据传输，将数据通过网络从一台设备传输到另一台设备 网络 两台或多台设备通过一定物理设备连接起来构成了网络 网络又分为: 局域网:覆盖范围最小，仅仅覆盖一个教室或一个机房城域网:覆盖范围较大，可以…...
kafka配置远程连接
要想实现在本地连接服务器的kafka，则必须在远程kafka配置远程连接 默认的 kafka 配置是无法远程访问的，解决该问题有几个方案。 方案1 advertised.listenersPLAINTEXT://IP:9092 注意必须是 ip，不能是 hostname 方案2 advertised.listene…...
css实现渐变色border
方式1 div {border: 4px solid;border-image: linear-gradient(to right, #8f41e9, #578aef) 1; }/* 或者 */ div {border: 4px solid;border-image-source: linear-gradient(to right, #8f41e9, #578aef);border-image-slice: 1; }作者：MudOnTire 链接：…...
管理 IBM Spectrum LSF
管理 IBM Spectrum LSF 了解如何管理 IBM Spectrum LSF 集群，控制守护程序，更改集群配置以及使用主机和队列。 管理 LSF 作业和作业调度策略。 查看作业信息和控制作业。 了解如何配置资源并将其分配给 LSF 作业。 了解如何在 LSF 集群中提交࿰…...
117页数字化转型与产业互联网发展趋势及机会分析报告PPT
导读：原文《》（获取来源见文尾），本文精选其中精华及架构部分，逻辑清晰、内容完整，为快速形成售前方案提供参考。 喜欢文章，您可以点赞评论转发本文，了解更多内容请私信：方…...
【JavaWeb】实训的长篇笔记（上）
JavaWeb的实训是学校的一门课程，老师先讲解一些基础知识，然后让我们自己开发一个比较简单的Web程序。可涉及的知识何其之多，不是实训课的 3 周时间可以讲得完的，只是快速带过。他说：重点是Web开发的流程。 我的实训草草…...
未来机器人的大脑：如何用神经网络模拟器实现更智能的决策？
编辑：陈萍萍的公主一点人工一点智能 未来机器人的大脑：如何用神经网络模拟器实现更智能的决策？RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战，在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...
深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架，用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录，以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...
SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外，K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案，全安装在K8S群集中。 具体可参…...
css实现圆环展示百分比，根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...
Swift 协议扩展精进之路：解决 CoreData 托管实体子类的类型不匹配问题（下）
概述 在 Swift 开发语言中，各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过，在涉及到多个子类派生于基类进行多态模拟的场景下，…...
（二）TensorRT-LLM | 模型导出（v0.20.0rc3）
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述，后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作，其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...
DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增：通道注意力模块（SE模块） class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...
【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言： 在人工智能快速发展的浪潮中，快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型（LLM）。该模型代表着该领域的重大突破，通过独特方式融合思考与非思考…...
Frozen-Flask ：将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是：将一个 Flask Web 应用生成成纯静态 HTML 文件，从而可以部署到静态网站托管服务上，如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...