【数据结构OJ题】设计循环队列
原题链接:https://leetcode.cn/problems/design-circular-queue/
1. 题目描述

2. 循环队列的概念和结构
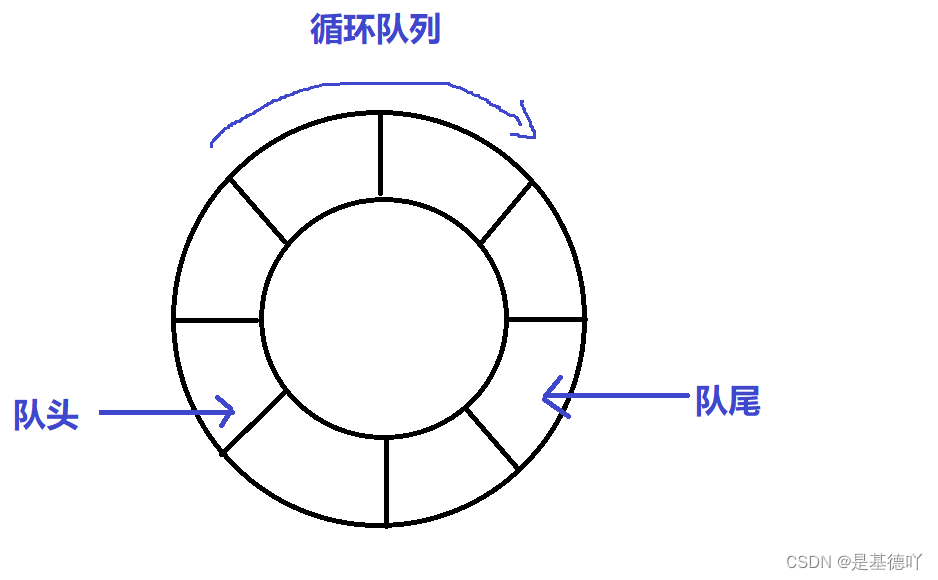
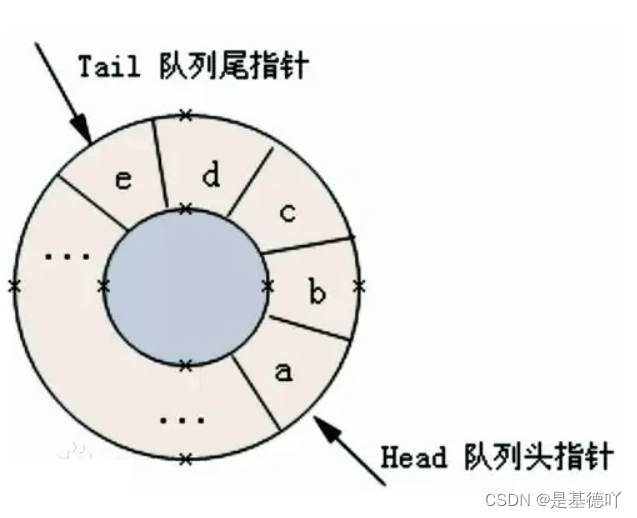
为充分利用向量空间,克服"假溢出"现象的方法是:将向量空间想象为一个首尾相接的圆环,并称这种向量为循环向量。存储在其中的队列称为循环队列(Circular Queue)。循环队列是把顺序队列首尾相连,把存储队列元素的表从逻辑上看成一个环,成为循环队列。
在操作系统课程讲解生产者消费者模型时可以就会使用循环队列。
循环队列可以使用数组实现,也可以使用循环链表实现
3. 思路分析
通过一个定长数组实现循环队列。
入队:首先要判断队列是否已满,再进行入队的操作,入队操作需要考虑索引循环的问题,当索引越界,需要让它变成最小值。
出队:首先要判断队列是否为空,再进行出队操作,出队也需要考虑索引循环的问题。
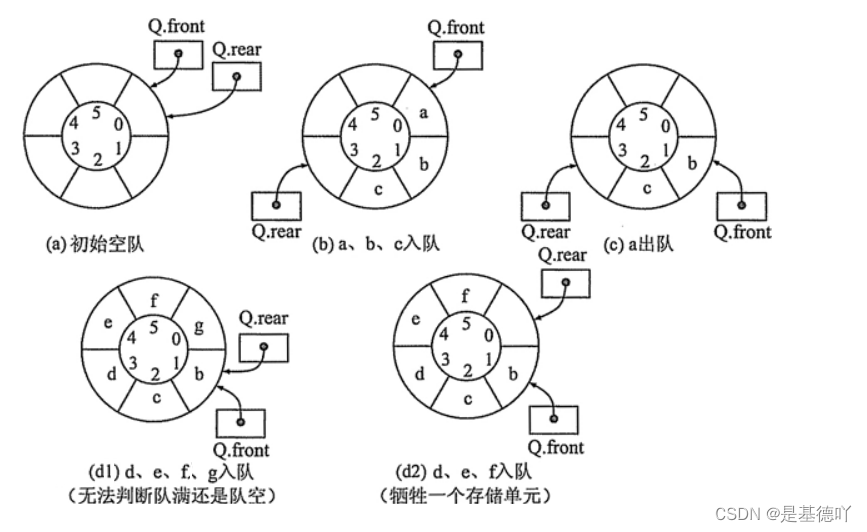
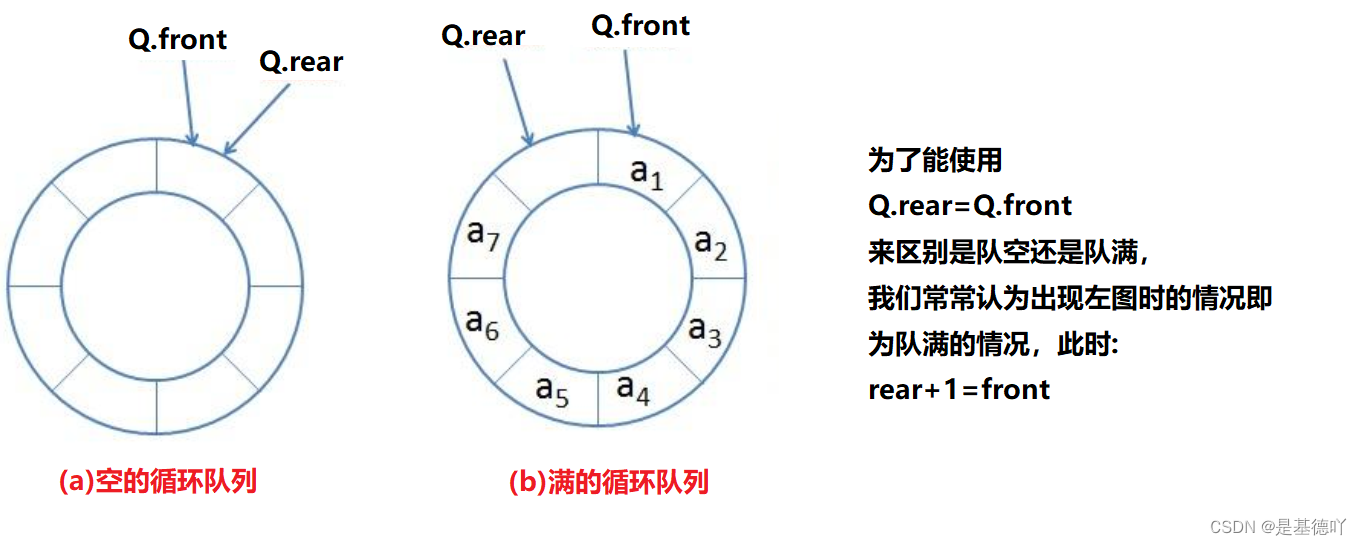
判空: 队头 == 队尾
判满: 队尾 + 1 == 队头
4. 代码实现
typedef struct {int *a;int front;int rear;int k;
} MyCircularQueue;MyCircularQueue* myCircularQueueCreate(int k) {MyCircularQueue* obj=(MyCircularQueue*) malloc(sizeof(MyCircularQueue));//多开一个方便区分空和满obj->a=(int*)malloc(sizeof(int)*(k+1));obj->front=obj->rear=0;obj->k=k;return obj;
}bool myCircularQueueIsEmpty(MyCircularQueue* obj) {return obj->front==obj->rear;
}bool myCircularQueueIsFull(MyCircularQueue* obj) {return (obj->rear+1)%(obj->k+1)== obj->front;
}bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {if(myCircularQueueIsFull(obj))return false;obj->a[obj->rear]=value;obj->rear++;obj->rear%=(obj->k+1);return true;
}bool myCircularQueueDeQueue(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj))return false;++obj->front;obj->front%=(obj->k+1);return true;
}int myCircularQueueFront(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj))return -1;elsereturn obj->a[obj->front];
}int myCircularQueueRear(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj))return -1;elsereturn obj->a[(obj->rear+obj->k)%(obj->k+1)];
}void myCircularQueueFree(MyCircularQueue* obj) {free(obj->a);free(obj);
}/*** Your MyCircularQueue struct will be instantiated and called as such:* MyCircularQueue* obj = myCircularQueueCreate(k);* bool param_1 = myCircularQueueEnQueue(obj, value);* bool param_2 = myCircularQueueDeQueue(obj);* int param_3 = myCircularQueueFront(obj);* int param_4 = myCircularQueueRear(obj);* bool param_5 = myCircularQueueIsEmpty(obj);* bool param_6 = myCircularQueueIsFull(obj);* myCircularQueueFree(obj);
*/
相关文章:

【数据结构OJ题】设计循环队列
原题链接:https://leetcode.cn/problems/design-circular-queue/ 1. 题目描述 2. 循环队列的概念和结构 为充分利用向量空间,克服"假溢出"现象的方法是:将向量空间想象为一个首尾相接的圆环,并称这种向量为循环向量。…...

Java 中创建对象有哪些方式?
目录 面试回答 使用 new 关键字 使用反射机制 使用 Class 类的 newInstance() 方法 使用 Constructor 类的 newInstance 方法 使用 clone 方法 使用反序列化 使用方法句柄 使用 Unsafe 分配内存 面试回答 使用 new 关键字 这是我们最常用的、也是最简单的创建对象的方…...

Kafka 消息发送和消费流程
发送消息 流程如下: Producer 端直接将消息发送到 Broker 中的 Leader 分区中Broker 对应的 Leader 分区收到消息会先写入 Page Cache,定时刷盘进行持久化(顺序写入磁盘)Follower 分区拉取 Leader 分区的消息,并保持…...
)
UVa10048 Audiophobia(floyd)
题意 给出一个图,图中的边表示从点u到点v路径上的噪音。给出q个查询,问从u到v所经路径上的最小噪音 思路 在使用floyd计算点对之间的路径时, D u , v k m i n { D u , v k − 1 , m a x { D u , k k − 1 , D k , v k − 1 } } D_{u, v}^…...
Redis概述
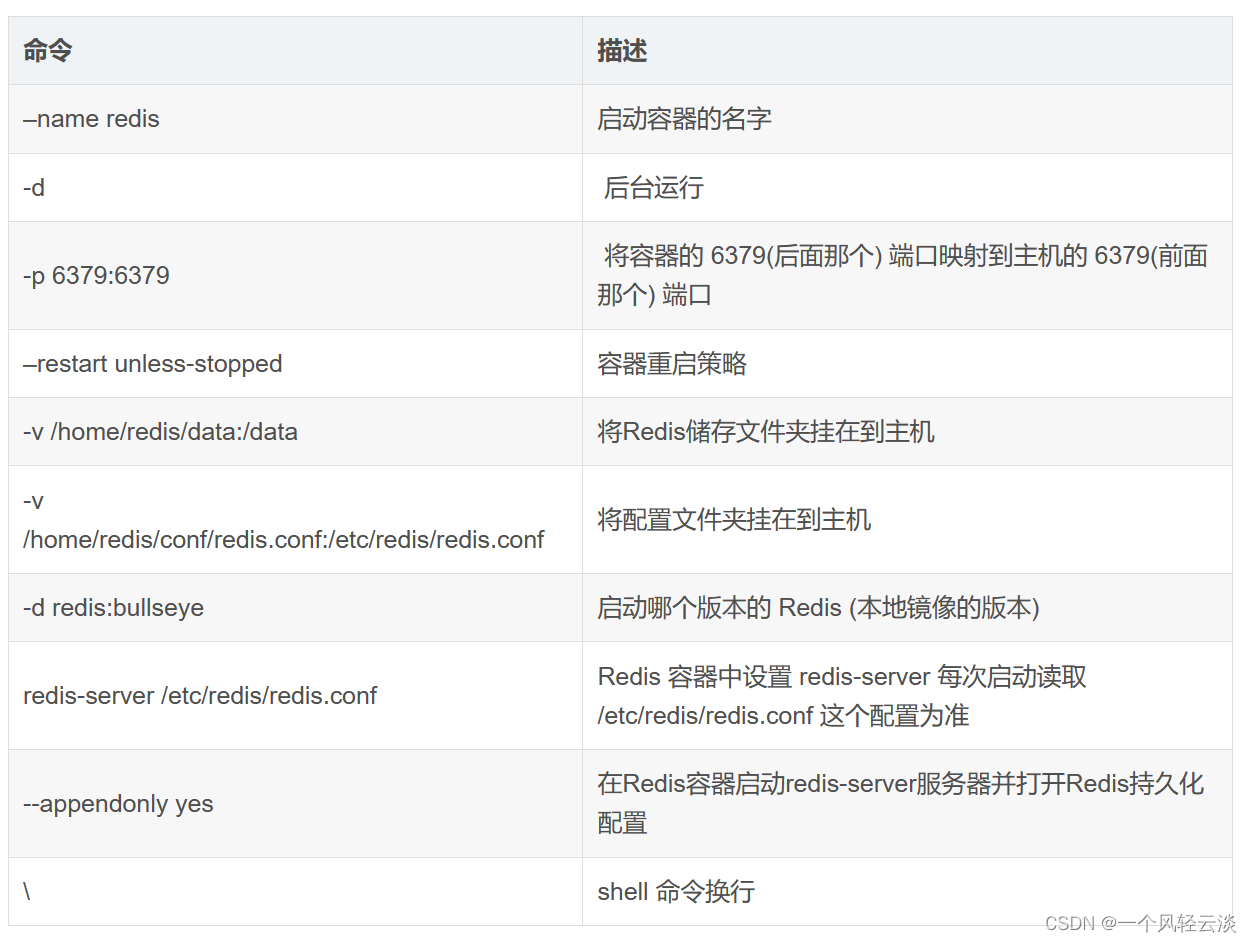
目录 Redis - 概述 使用场景 如何安装 Window 下安装 Linux 下安装 docker直接进行安装 下载Redis镜像 Redis启动检查常用命令 Redis - 概述 redis是一款高性能的开源NOSQL系列的非关系型数据库,Redis是用C语言开发的一个开源的高键值对(key value)数据库,官方提供测试…...

MsrayPlus多功能搜索引擎采集软件
MsrayPlus多功能搜索引擎采集软件 摘要: 本文介绍了一款多功能搜索引擎软件-MsrayPlus,该软件能够根据关键词从搜索引擎中检索相关数据,并提供搜索引擎任务、爬虫引擎任务和联系信息采集三大功能。我们将分析该软件在不同领域的应用…...

机器学习之概率论
最近,在了解机器学习相关的数学知识,包括线性代数和概率论的知识,今天,回顾了概率论的知识,贴上几张其他博客的关于概率论的图片,记录学习过程。...

【深度学习 | 数据可视化】 视觉展示分类边界: Perceptron模型可视化iris数据集的决策边界
🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&…...
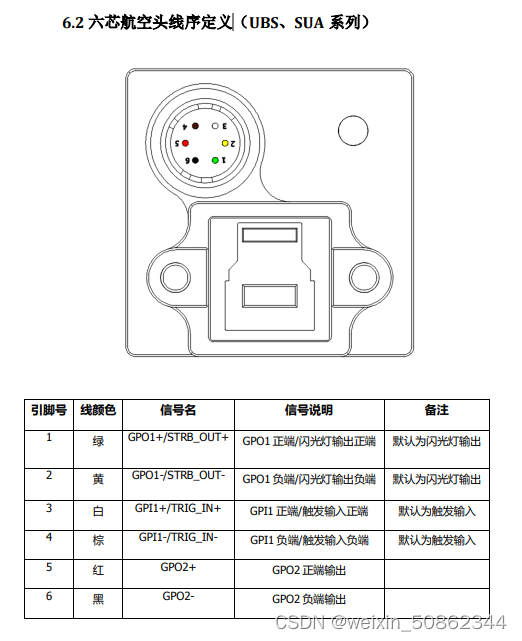
【计算机视觉】相机基本知识(还在更新)
1.面阵工业相机与线阵工业相机 1.1 基本概念区别 面阵相机则主要采用的连续的、面状扫描光线来实现产品的检测; 线阵相机即利用单束扫描光来进行物体扫描的工作的。 1.2 优缺点 (1)面阵CCD工业相机: 优点:应用面…...
(类嵌套时,成员函数以及类声明定义的顺序)小demo)
C++ (友元)(类嵌套时,成员函数以及类声明定义的顺序)小demo
#include<iostream> using namespace std; class Building; //1.因为Goodgay类需要声明Building类变量, //所以Building类必须Goodgay类之前声明(前向声明); class GoodGay { public:GoodGay();void visit(); private:Build…...

前端实习第五周周记
前言 每一天做了什么还是要记录一下,不然过两天后就会发现,慢慢遗忘自己的收获与做过的东西。 这周做的是医学检验系统的样本库部分。由于是公司的代码所以不能交代具体,那么久聊一下每天具体做了些什么以及我的一些收获。 周一 周一上午…...

【图论】Floyd算法
一.简介 Floyd算法,也称为Floyd-Warshall算法,是一种用于解决所有节点对最短路径问题的动态规划算法。它可以在有向图或带权图中找到任意两个节点之间的最短路径。 Floyd算法的基本思想是通过中间节点逐步优化路径长度。它使用一个二维数组来存储任意两…...
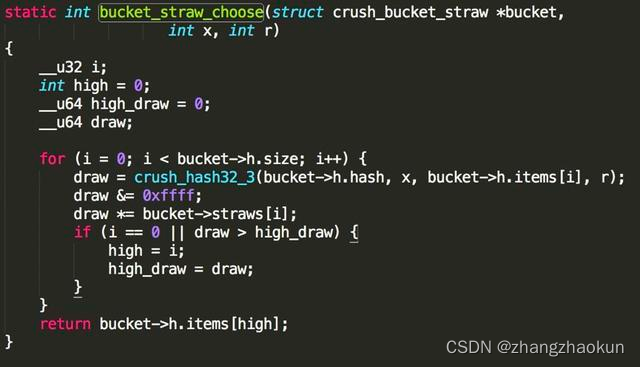
ceph数据分布
ceph的存储是无主结构,数据分布依赖client来计算,有两个条主要路径。 1、数据到PG 2、PG 到OSD 有两个假设: 第一,pg的数量稳定,可以认为保持不变; 第二, OSD的数量可以增减,OSD的…...
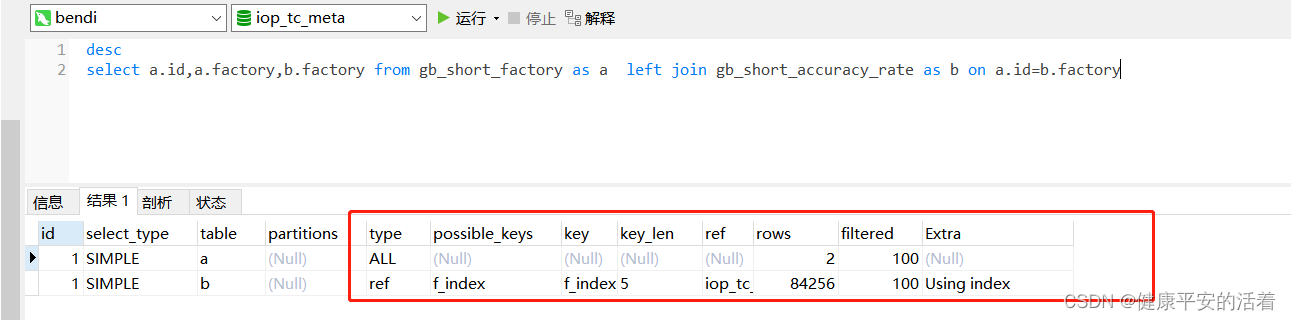
mysql的两张表left join 进行关联后,索引进行优化案例
一 mysql的案例 1.1 不加索引情况 1.表1没加索引 2.表2没加索引 3.查看索引 1.2 添加索引 1.表1添加索引 2.表2添加索引 3.查看...
2018年3月全国计算机等级考试真题(语言二级C)
2018年3月全国计算机等级考试真题(语言二级C) 第1题 设有定义:char s[81];int i0;以下不能将一行带有空格的字符串正确读入的语句或语句组是 A. while((s[i]getchar())!\n);s[i]\0; B. scanf("%s",s); C.…...

java.util.Timer简介以及简单使用示例
一、简介 定时器(Timer)是一个工具类,用于安排任务(java.util.TimerTask)在指定时间后执行或以指定的时间间隔重复执行。它可以用于执行定时任务、定时调度和时间延迟等操作。 定时器(Timer)可以…...

C语言笔试训练【第12天】
文章目录 1、请阅读以下程序,其运行结果是( )2、假设编译器规定 int 和 short 类型长度分别为32位和16位,若有下列C语言语句,则 y 的机器数为( )3、下列程序的输出结果是什么( &…...

外网连接局域网的几种方式?快解析内网穿透安全便利吗?
外网连接局域网是一项网络连接中的关键技术,它能够让远程用户通过互联网访问内部局域网中的资源和服务。外网连接局域网为企业提供了更大的灵活性和便捷性,但也需要严格的安全措施来防止未经授权的访问。 外网连接局域网的几种方式 在将外网连接到局域…...
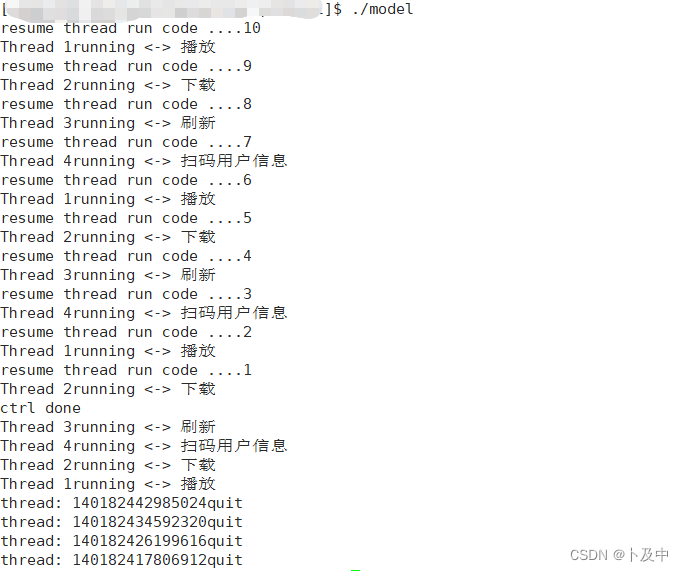
基于互斥锁的生产者消费者模型
文章目录 生产者消费者 定义代码实现 / 思路完整代码执行逻辑 / 思路 局部具体分析model.ccfunc(消费者线程) 执行结果 生产者消费者 定义 生产者消费者模型 是一种常用的 并发编程模型 ,用于解决多线程或多进程环境下的协作问题。该模型包含…...
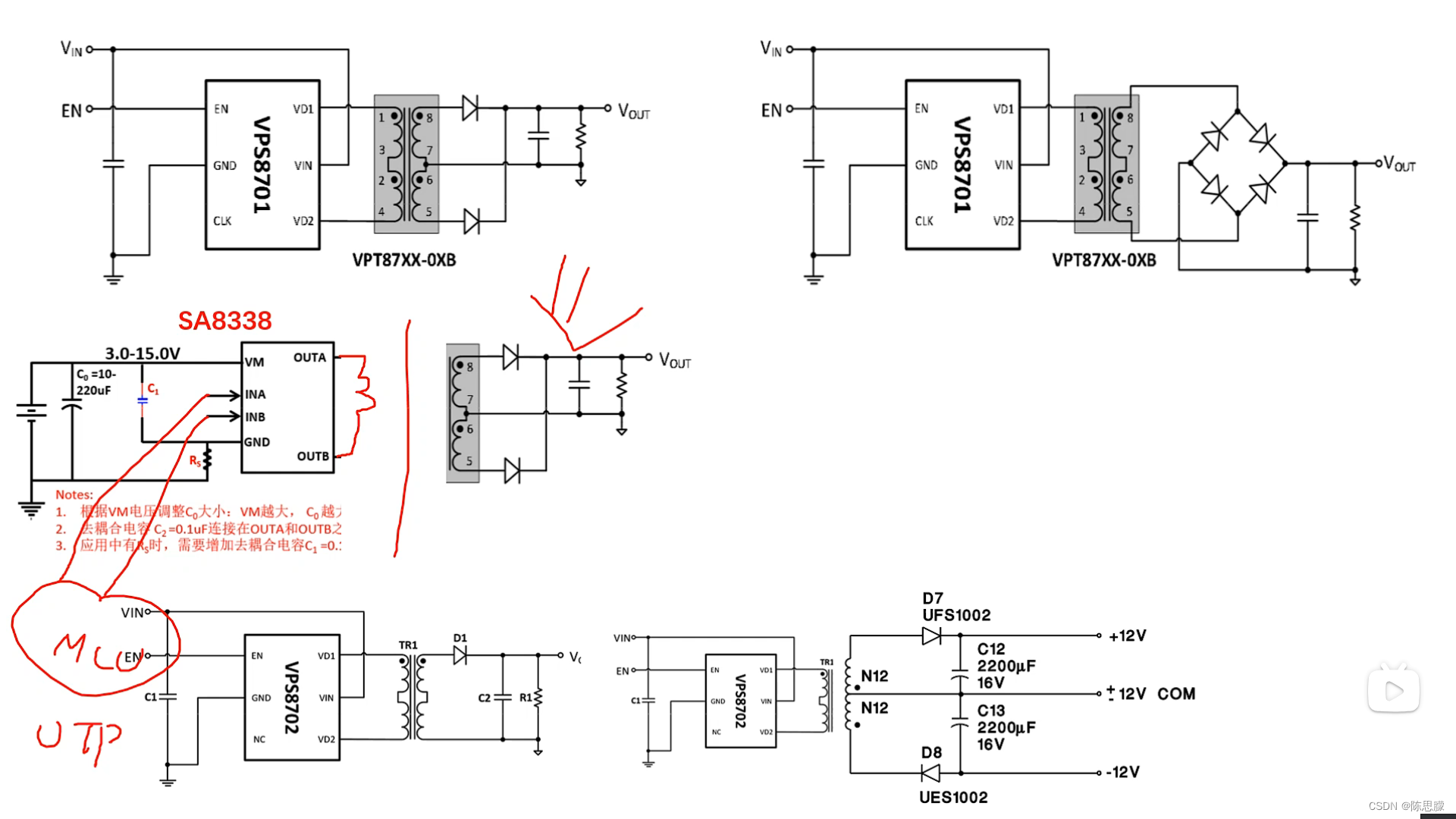
USB隔离器电路分析,SA8338矽塔sytatek电机驱动,源特科技VPS8701,开关电源,电源 大师
一、 USB隔离器电路分析 进行usb隔离可以使用USB隔离模块 ADUM3160 ADUM4160 注意:B0505S 最大带载0.16A,副边需要带载能力需要改变方案 比如移动硬盘至少需要0.5A 用充电宝、18650、设计5V1A输出电源 二、 1A隔离电压方案...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
