【图论】Floyd算法
一.简介
![]()
Floyd算法,也称为Floyd-Warshall算法,是一种用于解决所有节点对最短路径问题的动态规划算法。它可以在有向图或带权图中找到任意两个节点之间的最短路径。
Floyd算法的基本思想是通过中间节点逐步优化路径长度。它使用一个二维数组来存储任意两个节点之间的最短路径长度,并通过不断更新这个数组来得到最终的结果。
算法的步骤如下:
- 初始化一个二维数组,用于存储节点之间的最短路径长度。
- 将数组的初始值设置为图中节点之间的直接距离,如果两个节点之间没有直接连接,则距离为无穷大。
- 对于每个节点k,遍历所有节点对(i, j),并尝试通过节点k来优化路径长度。如果通过节点k可以获得更短的路径,则更新数组中的值。
- 重复步骤3,直到所有节点对的最短路径长度都被计算出来。
Floyd算法的时间复杂度为O(n^3),其中n是图中节点的数量。它适用于解决稠密图(边数接近节点数的平方)的最短路径问题,但对于稀疏图来说,可能存在更高效的算法。
总的来说,Floyd算法是一种非常经典且实用的算法,可以在有向图或带权图中找到任意两个节点之间的最短路径。
二.存图方法
因为是解决多源最短路,所以使用邻接矩阵存图。
三.原理
逐渐利用每个点进行搭桥,实现中转功能。过程中带有dp的思想,因为要使用搭完桥之后的最短路径进行再次搭桥,从而实现最优解。
四.核心代码
for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)g[i][j]=min(g[i][j],g[i][k]+g[k][j]);五.很重要的一道题
P1119 灾后重建 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
六.此题好的原因
考察了对选手floyd算法的进一步理解,而不是单纯的背板子
七.难点
最短路径是很好求的,但题目要求的时间是个大难题。有些路在一个时间点并不能用,更不能起到搭桥作用。所以输出答案时,并不能只考虑起点和终点不能走,还有考虑不能走对其他点最短路的影响。
八.解决方案
既然没到时间就不能用这个点搭桥,那我们在计算整体最短路时不用不就行了吗?在floyd算法中,第一重遍历中的k就是用这个点进行搭桥,那我们就没到时间这前就不遍历即可。
九.参考代码
#include<iostream>
#include<cstdio>
#define N 205
using namespace std;
int n,m;
int a[N];
int f[N][N];//邻接矩阵存边
inline void updata(int k){for(int i=0;i<n;i++)for(int j=0;j<n;j++)if(f[i][j]>f[i][k]+f[j][k])f[i][j]=f[j][i]=f[i][k]+f[j][k];//用这个新的更新所有前面的 return;
}
int main(){cin>>n>>m;for(int i=0;i<n;i++)scanf("%d",a[i]);//依次输入每一个村庄建立完成时需要的时间for(int i=0;i<n;i++)for(int j=0;j<n;j++){f[i][j]=1e9;//初始化为保证它不爆炸范围内的最大值 }for(int i=0;i<n;i++)f[i][i]=0;int s1,s2,s3;for(int i=1;i<=m;i++){scanf("%d%d%d",&s1,&s2,&s3);f[s1][s2]=f[s2][s1]=s3;//初始化边长 }int q;cin>>q;int now=0;for(int i=1;i<=q;i++){//处理各询问 scanf("%d%d%d",&s1,&s2,&s3); //s3为可用时间点 ,s1为x点,s2为y点 while(a[now]<=s3&&now<n){updata(now);//依次更新点,使它可以被用来更新其他的点 now++;}if(a[s1]>s3||a[s2]>s3)cout<<-1<<endl;else {if(f[s1][s2]==1e9)cout<<-1<<endl;else cout<<f[s1][s2]<<endl;}}return 0;
} 相关文章:

【图论】Floyd算法
一.简介 Floyd算法,也称为Floyd-Warshall算法,是一种用于解决所有节点对最短路径问题的动态规划算法。它可以在有向图或带权图中找到任意两个节点之间的最短路径。 Floyd算法的基本思想是通过中间节点逐步优化路径长度。它使用一个二维数组来存储任意两…...
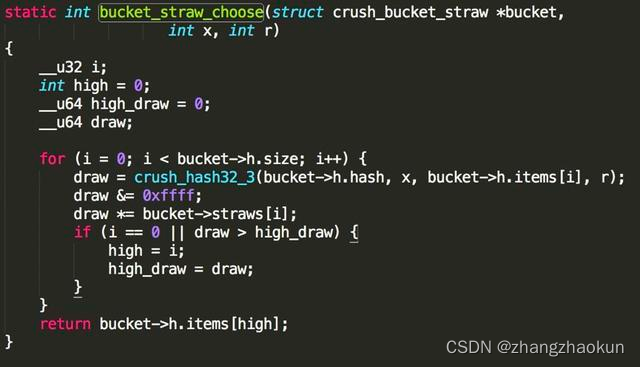
ceph数据分布
ceph的存储是无主结构,数据分布依赖client来计算,有两个条主要路径。 1、数据到PG 2、PG 到OSD 有两个假设: 第一,pg的数量稳定,可以认为保持不变; 第二, OSD的数量可以增减,OSD的…...
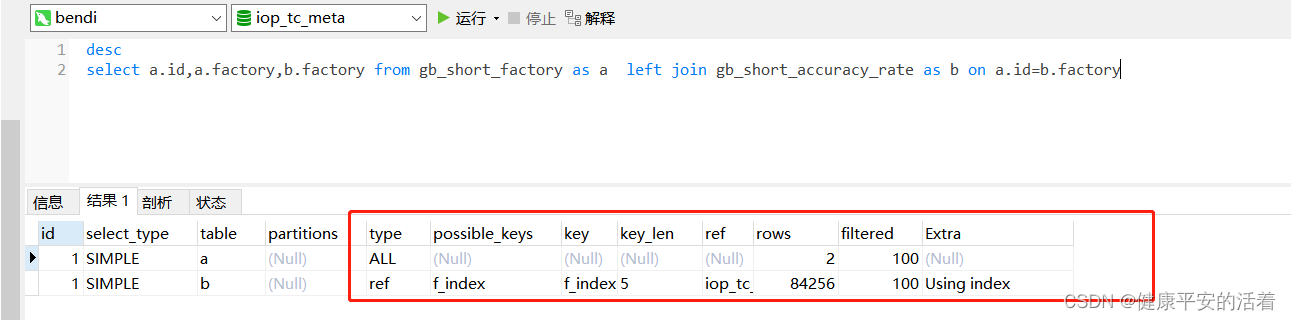
mysql的两张表left join 进行关联后,索引进行优化案例
一 mysql的案例 1.1 不加索引情况 1.表1没加索引 2.表2没加索引 3.查看索引 1.2 添加索引 1.表1添加索引 2.表2添加索引 3.查看...
2018年3月全国计算机等级考试真题(语言二级C)
2018年3月全国计算机等级考试真题(语言二级C) 第1题 设有定义:char s[81];int i0;以下不能将一行带有空格的字符串正确读入的语句或语句组是 A. while((s[i]getchar())!\n);s[i]\0; B. scanf("%s",s); C.…...

java.util.Timer简介以及简单使用示例
一、简介 定时器(Timer)是一个工具类,用于安排任务(java.util.TimerTask)在指定时间后执行或以指定的时间间隔重复执行。它可以用于执行定时任务、定时调度和时间延迟等操作。 定时器(Timer)可以…...

C语言笔试训练【第12天】
文章目录 1、请阅读以下程序,其运行结果是( )2、假设编译器规定 int 和 short 类型长度分别为32位和16位,若有下列C语言语句,则 y 的机器数为( )3、下列程序的输出结果是什么( &…...

外网连接局域网的几种方式?快解析内网穿透安全便利吗?
外网连接局域网是一项网络连接中的关键技术,它能够让远程用户通过互联网访问内部局域网中的资源和服务。外网连接局域网为企业提供了更大的灵活性和便捷性,但也需要严格的安全措施来防止未经授权的访问。 外网连接局域网的几种方式 在将外网连接到局域…...
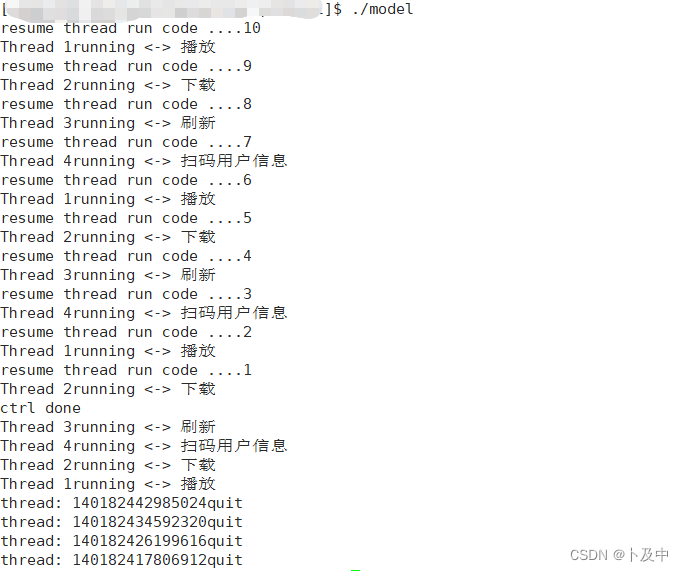
基于互斥锁的生产者消费者模型
文章目录 生产者消费者 定义代码实现 / 思路完整代码执行逻辑 / 思路 局部具体分析model.ccfunc(消费者线程) 执行结果 生产者消费者 定义 生产者消费者模型 是一种常用的 并发编程模型 ,用于解决多线程或多进程环境下的协作问题。该模型包含…...
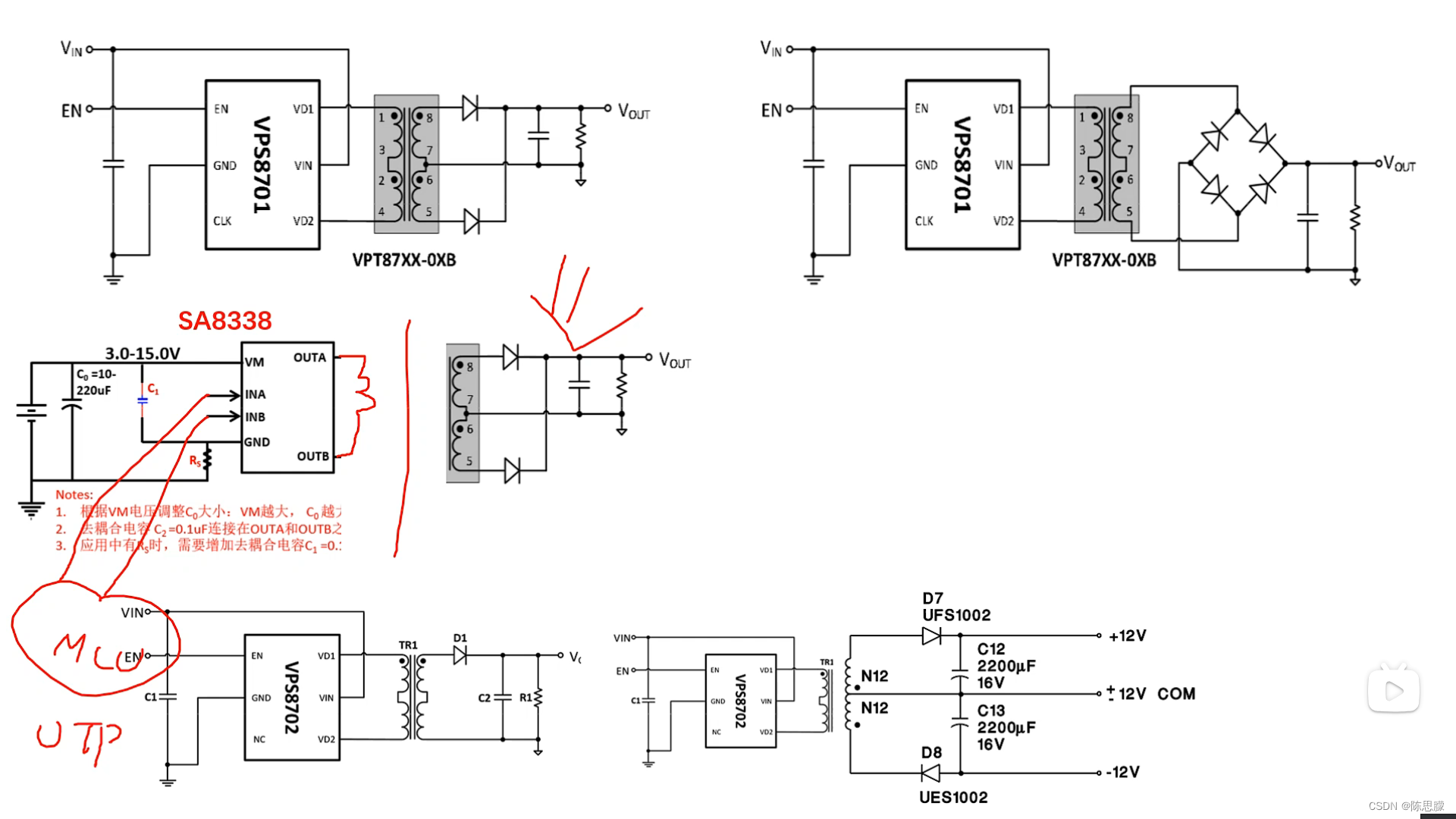
USB隔离器电路分析,SA8338矽塔sytatek电机驱动,源特科技VPS8701,开关电源,电源 大师
一、 USB隔离器电路分析 进行usb隔离可以使用USB隔离模块 ADUM3160 ADUM4160 注意:B0505S 最大带载0.16A,副边需要带载能力需要改变方案 比如移动硬盘至少需要0.5A 用充电宝、18650、设计5V1A输出电源 二、 1A隔离电压方案...

TPC-DS 测试是否支持 Glue Data Catalog?
在上一篇文章《在Hive/Spark上执行TPC-DS基准测试 (PARQUET格式)》中,我们详细介绍了具体的操作方法,当时的集群使用的是Hive Metastore,所有操作均可成功执行。当集群启用 Glue Data Catalog 时,在执行add_constraints.sql时会报错: Optimizing table date_dim (1/24).…...
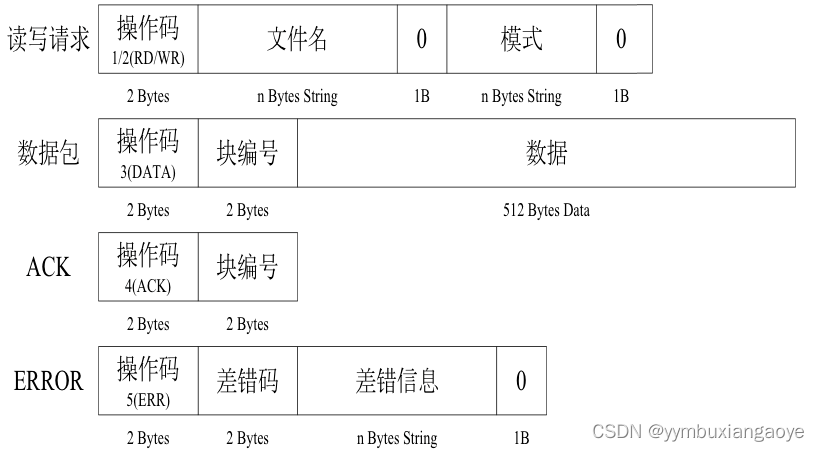
网络编程(8.14)TCP并发服务器模型
作业: 1. 多线程中的newfd,能否修改成全局,不行,为什么? 2. 多线程中分支线程的newfd能否不另存,直接用指针间接访问主线程中的newfd,不行,为什么? 多线程并发服务器模型原代码&…...

认识负载均衡||WEBSHELL
目录 一、负载均衡 1.nginx负载均衡算法 2.nginx反向代理-负载均衡 二、webshell 1.构造不含数字和字母的webshell 2.如何绕过 一、负载均衡 1.nginx负载均衡算法 (1)轮询(默认)每个请求按时间顺序逐一分配到不同的后端服务&…...

Chapter 15: Object-Oriented Programming | Python for Everybody 讲义笔记_En
文章目录 Python for Everybody课程简介Object-oriented programmingManaging larger programsGetting startedUsing objectsStarting with programsSubdividing a problemOur first Python objectClasses as typesObject lifecycleMultiple instancesInheritanceSummaryGlossa…...

模板编程-成员特化
成员特化:类模板特化除了可以对整个类进行特化外,可以只针对某部分成员函数进行特化 全类特化和成员特化都属于全局特化 #define _CRT_SECURE_NO_WARNINGS #include <iostream> #include <cstring>template<typename T> class CMath { public:CMath(const…...

信安通用基础知识
文章目录 密码学经典误区PGP优良保密协议信安经典其它安全手段XSS与CSRF cross site request forgeryCSRF的利用逻辑CSRF示例CSRF防范检查Referer字段添加校验token XSS cross site scripting common weakness enumeration常见密码api误用(摘自毕设参考文献…...
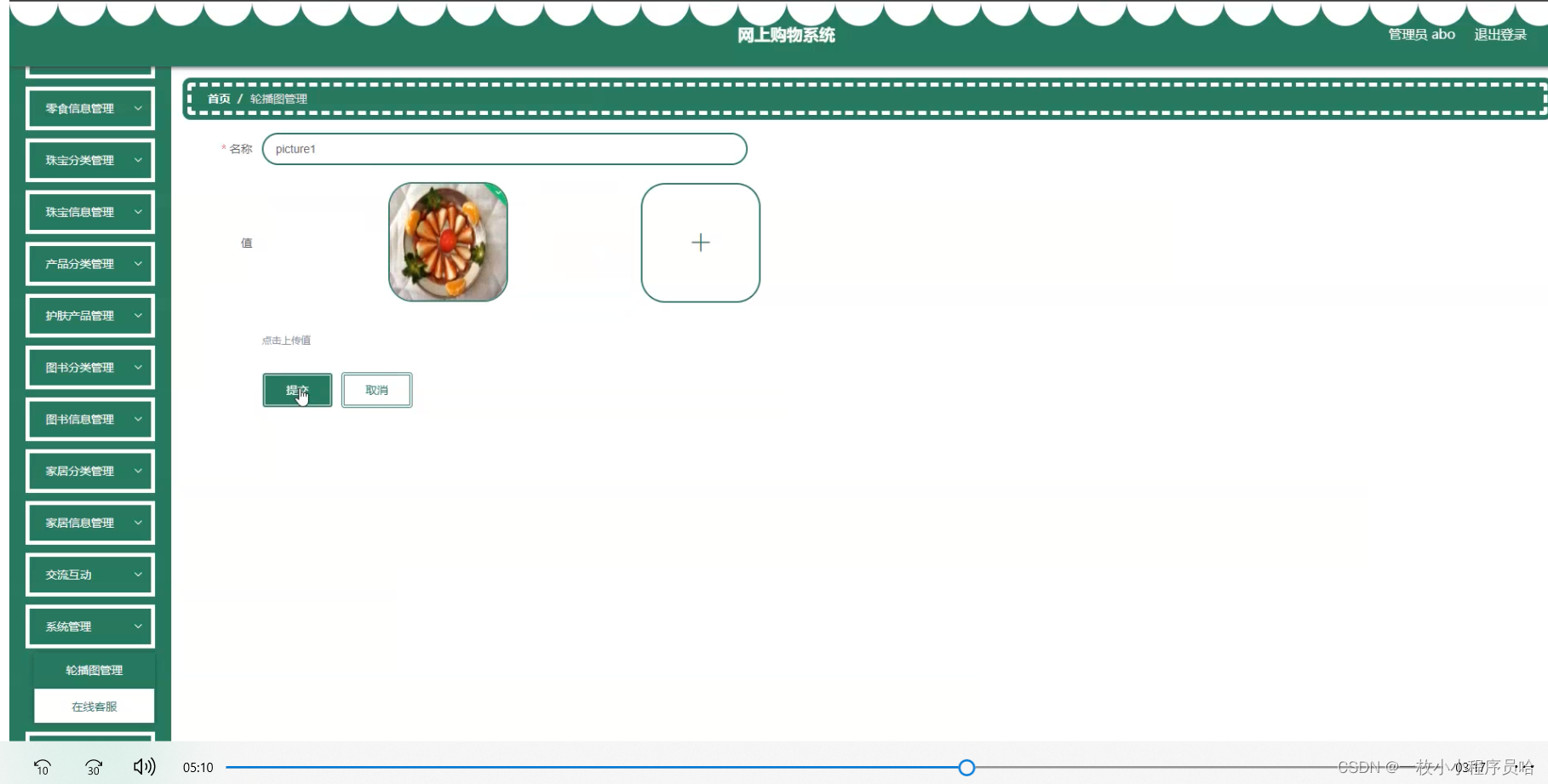
网上购物系统的设计与实现/在线商城/基于spring boot的电商平台/基于Java的商品销售系统
摘 要 本毕业设计的内容是设计并且实现一个基于Springboot的网上购物系统。它是在Windows下,以MYSQL为数据库开发平台,Tomcat网络信息服务作为应用服务器。网上购物系统的功能已基本实现,主要包括用户管理、数码分类管理、数码产品管理、服…...

uniapp项目-配置store文件夹
1.创建store.js 说明:创建一个新的 Vuex Store 实例,配置 Store 中的模块。 import Vue from vue; import Vuex from vuex; // 导入两个 Vuex 模块:moduleCart 和 moduleUser import moduleCart from /store/cart.js; import moduleUser fr…...
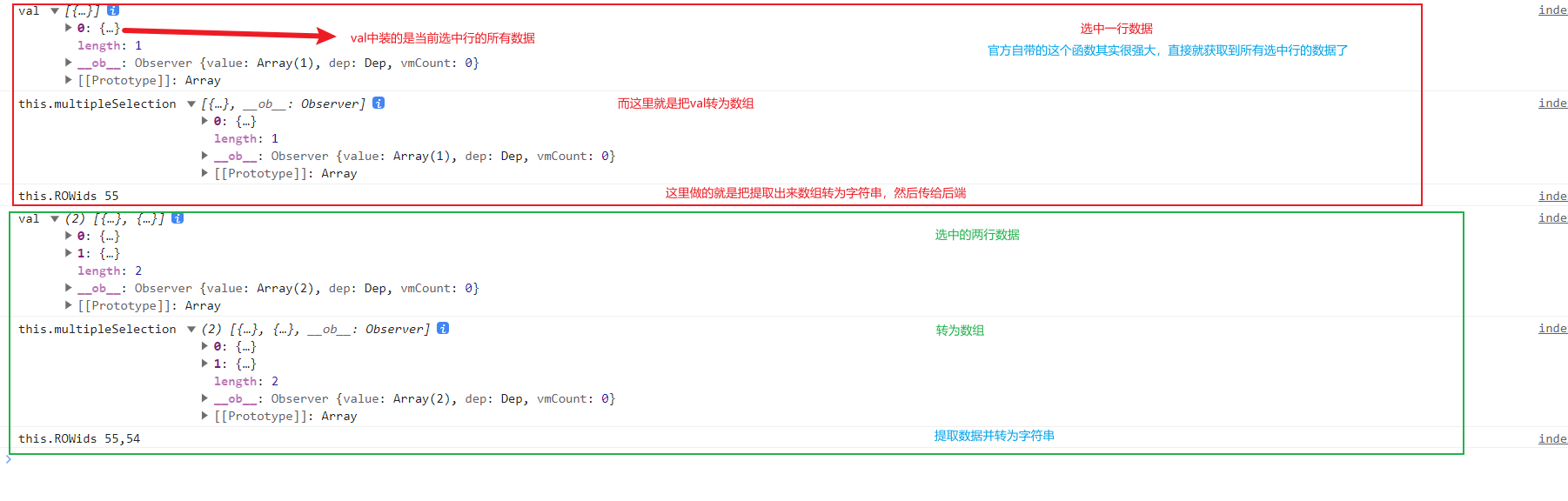
element表格多选实现
表格实现多选 实现表格多选很简单,只需要在表格里加上一列即可,加完之后就会在表格里出现一列白色的四方块按钮,可以多选,也可以单选 <el-table-columntype"selection"width"55"align"center"&…...

宠物智能自动喂食器方案设计
据相关数据表明,2019年全国城镇宠物犬猫数量达到9915万只,增幅达到8.4%,消费市场规模达2024亿元,比2018年增长18.5%,整体呈现持续大幅增长的态势。而养宠人群的主力,为25岁至38岁年轻人,都市白领…...

学习笔记230818---对于promise失败状态处理的重要性
问题描述: 在项目中经常会出现如上的问题,这是因为,用promise封装的接口或第三方组件方法,如果只对成功的状态做处理,就会造成页面出错,报error。 解决方法 then()的末尾加上.catch(()>{})对失败的状态…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
