浙大数据结构第八周之08-图7 公路村村通
题目详情:
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
输入格式:
输入数据包括城镇数目正整数N(≤1000)和候选道路数目M(≤3N);随后的M行对应M条道路,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见,城镇从1到N编号。
输出格式:
输出村村通需要的最低成本。如果输入数据不足以保证畅通,则输出−1,表示需要建设更多公路。
输入样例:
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
输出样例:
12主要思路:
先补一下邻接表建图
邻接表的处理方法:
(1)图中顶点用一个一维数组存储,当然,顶点也可以用单链表来存储,不过,数组可以较容易的读取顶点的信息,更加方便。
(2)图中每个顶点vi的所有邻接点构成一个线性表,由于邻接点的个数不定,所以,用单链表存储,无向图称为顶点vi的边表,有向图则称为顶点vi作为弧尾的出边表。
例如,下图就是一个无向图的邻接表的结构:
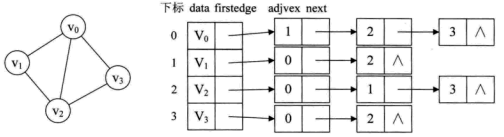
从图中可以看出,顶点表的各个结点由data和firstedge两个域表示,
data是数据域,存储顶点的信息,
firstedge是指针域,指向边表的第一个结点,即此顶点的第一个邻接点。
边表结点由adjvex和next两个域组成。
adjvex是邻接点域,存储某顶点的邻接点在顶点表中的下标,(可以通过此下标在一维顶点数组中查询到这个顶点的信息)
next则存储指向边表中下一个结点的指针。
数据结构一:边:
typedef struct ENode *PtrToENode;
struct ENode{Vertex V1, V2; /* 有向边<V1, V2> */WeightType Weight; /* 权重 */
};
typedef PtrToENode Edge;数据结构二:邻接点
/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{Vertex AdjV; /* 邻接点下标 */WeightType Weight; /* 边权重 */PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};数据结构三:顶点表头节点
/* 顶点表头结点的定义 */
typedef struct Vnode{PtrToAdjVNode FirstEdge; /* 指向边表的第一个结点,即此顶点的第一个邻接点 */DataType Data; /* 存顶点的数据 *//* 注意:很多情况下,顶点无数据,此时Data可以不用出现 */
} AdjList[MaxVertexNum]; /* AdjList是邻接表类型 */
数据结构四:图节点
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{ int Nv; /* 顶点数 */int Ne; /* 边数 */AdjList G; /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */
初始化有顶点没有边的空图:
LGraph CreateGraph( int VertexNum )
{ /* 初始化一个有VertexNum个顶点但没有边的图 */Vertex V;LGraph Graph;Graph = (LGraph)malloc( sizeof(struct GNode) ); /* 建立图 */Graph->Nv = VertexNum;Graph->Ne = 0;/* 初始化邻接表头指针 *//* 注意:这里默认顶点编号从0开始,到(Graph->Nv - 1) */for (V=0; V<Graph->Nv; V++)Graph->G[V].FirstEdge = NULL; //将每个顶点的邻接链表的头结点指针设置为 NULL。return Graph;
}插入边(插入的时候是头插法)
void InsertEdge( LGraph Graph, Edge E )
{ /* 插入边 <V1, V2> *//* 为V2建立新的邻接点 */PtrToAdjVNode NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));NewNode->AdjV = E->V2;NewNode->Weight = E->Weight;/* 将V2插入V1的表头,插入的边表示从v1指向v2 */NewNode->Next = Graph->G[E->V1].FirstEdge;Graph->G[E->V1].FirstEdge = NewNode;/* 若是无向图,还要插入边 <V2, V1> *//* 为V1建立新的邻接点 */NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));NewNode->AdjV = E->V1;NewNode->Weight = E->Weight;/* 将V1插入V2的表头 */NewNode->Next = Graph->G[E->V2].FirstEdge;Graph->G[E->V2].FirstEdge = NewNode;
}
建图
LGraph BuildGraph()
{LGraph Graph;Edge E;Vertex V;int Nv, i;scanf("%d", &Nv); /* 读入顶点个数 */Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */ scanf("%d", &(Graph->Ne)); /* 读入边数 */if ( Graph->Ne != 0 ) { /* 如果有边 */ E = (Edge)malloc( sizeof(struct ENode) ); /* 建立边结点 */ /* 读入边,格式为"起点 终点 权重",插入邻接矩阵 */for (i=0; i<Graph->Ne; i++) {scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); /* 注意:如果权重不是整型,Weight的读入格式要改 */InsertEdge( Graph, E );}} /* 如果顶点有数据的话,读入数据 */for (V=0; V<Graph->Nv; V++) scanf(" %c", &(Graph->G[V].Data));return Graph;
}然后是Prim算法:
/* 邻接矩阵存储 - Prim最小生成树算法 */Vertex FindMinDist( MGraph Graph, WeightType dist[] )
{ /* 返回未被收录顶点中dist最小者 */Vertex MinV, V; WeightType MinDist = INFINITY;for (V=0; V<Graph->Nv; V++) {if ( dist[V]!=0 && dist[V]<MinDist) {/* 若V未被收录,且dist[V]更小 */MinDist = dist[V]; /* 更新最小距离 */MinV = V; /* 更新对应顶点 */}}if (MinDist < INFINITY) /* 若找到最小dist */return MinV; /* 返回对应的顶点下标 */else return ERROR; /* 若这样的顶点不存在,返回-1作为标记 */
}int Prim( MGraph Graph, LGraph MST )
{ /* 将最小生成树保存为邻接表存储的图MST,返回最小权重和 */WeightType dist[MaxVertexNum], TotalWeight;Vertex parent[MaxVertexNum], V, W;int VCount;Edge E;/* 初始化。默认初始点下标是0 */for (V=0; V<Graph->Nv; V++) {/* 这里假设若V到W没有直接的边,则Graph->G[V][W]定义为INFINITY */dist[V] = Graph->G[0][V];parent[V] = 0; /* 暂且定义所有顶点的父结点都是初始点0 */ }TotalWeight = 0; /* 初始化权重和 */VCount = 0; /* 初始化收录的顶点数 *//* 创建包含所有顶点但没有边的图。注意用邻接表版本 */MST = CreateGraph(Graph->Nv);E = (Edge)malloc( sizeof(struct ENode) ); /* 建立空的边结点 *//* 将初始点0收录进MST */dist[0] = 0;VCount ++;parent[0] = -1; /* 当前树根是0 */while (1) {V = FindMinDist( Graph, dist );/* V = 未被收录顶点中dist最小者 */if ( V==ERROR ) /* 若这样的V不存在 */break; /* 算法结束 *//* 将V及相应的边<parent[V], V>收录进MST */E->V1 = parent[V];E->V2 = V;E->Weight = dist[V];InsertEdge( MST, E );TotalWeight += dist[V];dist[V] = 0;VCount++;for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */if ( dist[W]!=0 && Graph->G[V][W]<INFINITY ) {/* 若W是V的邻接点并且未被收录 */if ( Graph->G[V][W] < dist[W] ) {/* 若收录V使得dist[W]变小 */dist[W] = Graph->G[V][W]; /* 更新dist[W] */parent[W] = V; /* 更新树 */}}} /* while结束*/if ( VCount < Graph->Nv ) /* MST中收的顶点不到|V|个 */TotalWeight = ERROR;return TotalWeight; /* 算法执行完毕,返回最小权重和或错误标记 */
}其实本题可以只用邻接矩阵构建的图(或邻接表构建的图)也能解决,因为本题只要求MST的权值,并没有考察更多MST的性质,不过就当巩固所学吧
代码实现:
#include <stdio.h>
#include <stdlib.h>
#define MAX_NODE_NUMS 1005
#define INFINITY 100000
#define TRUE 1
#define FALSE 0
#define NONE -1
#define ROOT 1
typedef int bool;
/*ListGraph的数据结构*/
/*边*/
typedef struct ENode ENode;
typedef ENode* PToEdgeNode;
struct ENode {int Start, End, Weight;
};
/*邻接点*/
typedef struct AdjVNode AdjVNode;
typedef AdjVNode* PToAdjVNode;
struct AdjVNode {int VertexIndex, Weight;PToAdjVNode Next;
};
/*头结点*/
typedef struct HeadNode HeadNode;
struct HeadNode {int Weight;PToAdjVNode FirstEdge;
};
/*图节点*/
typedef struct ListGraphNode ListGraphNode;
typedef ListGraphNode* ListGraph;
struct ListGraphNode {int EdgeNums, VertexNums;HeadNode AdjList[MAX_NODE_NUMS];
};
/*建一个空图*/
ListGraph CreateEmptyListGraph(int vertexNums) {ListGraph LGraph = (ListGraph)malloc(sizeof(ListGraphNode));LGraph->EdgeNums = 0; LGraph->VertexNums = vertexNums;for(int i = 0; i <= vertexNums; i++) {LGraph->AdjList[i].FirstEdge = NULL;}return LGraph;
}
/*插入边*/
void InsertEdgeInLGraph(ListGraph LGraph, PToEdgeNode edge) {/*插入<start, end>的边*/PToAdjVNode newVertex = (PToAdjVNode)malloc(sizeof(AdjVNode));newVertex->VertexIndex = edge->End;newVertex->Weight = edge->Weight;newVertex->Next = LGraph->AdjList[edge->Start].FirstEdge;LGraph->AdjList[edge->Start].FirstEdge = newVertex;/*插入<end,start>的边,这是因为无向图,如果是有向图可以省略*/newVertex = (PToAdjVNode)malloc(sizeof(AdjVNode));newVertex->VertexIndex = edge->Start;newVertex->Weight = edge->Weight;newVertex->Next = LGraph->AdjList[edge->End].FirstEdge;LGraph->AdjList[edge->End].FirstEdge = newVertex;return;
}
ListGraph BuildListGraph(int vertexNums, int edgeNums) {ListGraph LGraph = CreateEmptyListGraph(vertexNums);for(int i = 0; i < edgeNums; i++) {PToEdgeNode newEdge = (PToEdgeNode)malloc(sizeof(ENode));scanf("%d %d %d", &(newEdge->Start), &(newEdge->End), &(newEdge->Weight));InsertEdgeInLGraph(LGraph, newEdge);free(newEdge);}return LGraph;
}/*MatrixGraph的数据结构*/
typedef struct MatrixGraphNode MatrixGraphNode;
typedef MatrixGraphNode* MatrixGraph;
struct MatrixGraphNode {int VertexNums, EdgeNums;int Weight[MAX_NODE_NUMS][MAX_NODE_NUMS];
};
MatrixGraph CreateEmptyMatrixGraph(int vertexNums) {MatrixGraph MGraph = (MatrixGraph)malloc(sizeof(MatrixGraphNode));MGraph->VertexNums = vertexNums;MGraph->EdgeNums = 0;for(int i = 0; i <= vertexNums; i++) {for(int j = 0; j <= vertexNums; j++) {MGraph->Weight[i][j] = INFINITY;}}return MGraph;
}
void InsertEdgeInMGraph(int start, int end, int weight, MatrixGraph MGraph) {MGraph->Weight[start][end] = weight;MGraph->Weight[end][start] = weight;return;
}
MatrixGraph BuildMGraph(int vertexNums, int edgeNums) {MatrixGraph MGraph = CreateEmptyMatrixGraph(vertexNums);MGraph->EdgeNums = edgeNums;for(int i = 0; i < edgeNums; i++) {int start, end, weight;scanf("%d %d %d", &start, &end, &weight);InsertEdgeInMGraph(start, end, weight, MGraph);}return MGraph;
}
/*Prim算法*/
/*在剩余节点中找到与最小生成树权值最小的边*/
int FindMinDis(MatrixGraph MGraph, const int dis[]) {int minV = NONE;int minDist = INFINITY;for(int i = 1; i <= MGraph->VertexNums; i++) {if(dis[i] != FALSE && dis[i] < minDist) { //dist其实兼顾了Dijkstra中vis数组的作用minDist = dis[i];minV = i;}}return minV;
}
int Prim(MatrixGraph MGraph) {int dis[MAX_NODE_NUMS]; //dis[i]表示节点i到最小生成树的距离int parent[MAX_NODE_NUMS];int totalWeight = 0;int Vcount = 0;/*初始化dis和path数组,默认是从下标1开始,因为顶点从下标1开始*/for(int i = 1; i <= MGraph->VertexNums; i++) {dis[i] = MGraph->Weight[ROOT][i]; //由初始化可以看出,如果ROOT(定这个ROOT的原因是因为最小生成树只有一个根节点)~i两个节点之间有边,就初始化为权值,否则就初始化为INFINITYparent[i] = ROOT; //假设所有顶点的上一级顶点都是ROOT}/*开始建立最小生成树*/ListGraph MST = CreateEmptyListGraph(MGraph->VertexNums);dis[ROOT] = 0; //将顶点1作为最小生成树的根节点Vcount++;parent[ROOT] = NONE;while(TRUE) {int minV = FindMinDis(MGraph, dis);if(minV == NONE) break;/*将minV加入到最小生成树中*/PToEdgeNode newEdge = (PToEdgeNode)malloc(sizeof(ENode));newEdge->Start = parent[minV];newEdge->End = minV;newEdge->Weight = dis[minV];InsertEdgeInLGraph(MST, newEdge);Vcount++;totalWeight += dis[minV];dis[minV] = FALSE; //防止重复加入/*更新dis和path数组*/for(int i = 1; i <= MGraph->VertexNums; i++) {if(dis[i] != FALSE && MGraph->Weight[minV][i] < INFINITY) { //如果i是之前找到的最小顶点的邻接点并且没有收录if(dis[i] > MGraph->Weight[minV][i]) { //如果收录最小的节点minV后使得节点i到最小生成树MST的距离变小dis[i] = MGraph->Weight[minV][i]; parent[i] = minV;}}}free(newEdge);}free(MST);if(Vcount < MGraph->VertexNums) return NONE;return totalWeight;
}
int main() {int vertexNums, edgeNums;scanf("%d %d", &vertexNums, &edgeNums);MatrixGraph MGraph = BuildMGraph(vertexNums, edgeNums);printf("%d", Prim(MGraph));free(MGraph);return 0;
}相关文章:

浙大数据结构第八周之08-图7 公路村村通
题目详情: 现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。 输入格式: 输入数据包括城镇数目正整数N(≤1000)和候选道路数目M(…...

SpringBoot 解决跨域问题
同源策略(CORS):浏览器在解析发送的请求时,要求浏览器的路径与发送的请求的路径必须满足三个要求,即请求的协议、域名、端口号都相同,满足同源策略,才可以访问服务器,否则࿰…...

2023 年牛客多校第十场题解
C Multiplication 题意:定义 k k k-shift 数是满足 k x y ‾ y x ‾ k\overline{xy}\overline{yx} kxyyx 的数字。给定 k k k,求最大不超过 n n n 的 k k k-shift 数。 1 ≤ n ≤ 1 0 100 1 \le n \le 10^{100} 1≤n≤10100, 2 ≤…...

韦东山老师 RTOS 入门课程(一)RTOS 介绍,熟悉裸机的汇编逻辑
韦东山老师 RTOS 入门课程 课程链接:韦东山直播公开课:RTOS实战项目之实现多任务系统 第1节:裸机程序框架和缺陷_哔哩哔哩_bilibili RTOS 介绍 裸机:固定顺序执行。 中断:可以一直专心做循环里的事情,直…...
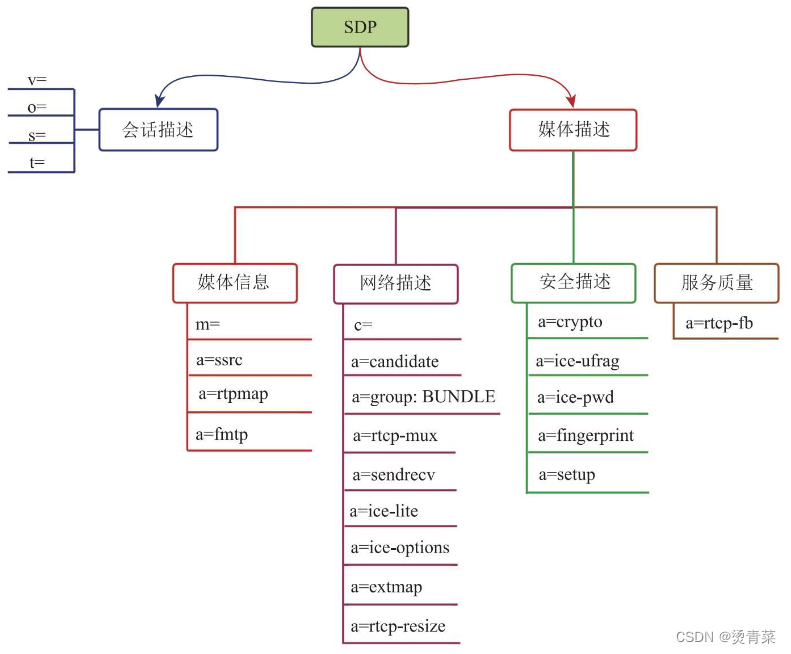
WebRTC | SDP详解
目录 一、SDP标准规范 1. SDP结构 2. SDP内容及type类型 二、WebRTC中的SDP结构 1. 媒体信息描述 (1)SDP中媒体信息格式 i. “artpmap”属性 ii. “afmtp”属性 (2)SSRC与CNAME (3)举个例子 &…...
springboot集成Oauth2.0授权包,5个接口文件配置详解)
Springboot 实践(9)springboot集成Oauth2.0授权包,5个接口文件配置详解
前文讲解实现了spring boot集成Oauth2.0,实现了授权服务器和资源服务器的搭建,并通过浏览器和postman测试,获取到了授权码,用携带授权码的URL能够争取范文到资源。 本文详细讲解spring boot集成Oauth2.0的几个重要文件接口&#…...
最新AI系统ChatGPT程序源码/支持GPT4/自定义训练知识库/GPT联网/支持ai绘画(Midjourney)+Dall-E2绘画/支持MJ以图生图
一、前言 SparkAi系统是基于国外很火的ChatGPT进行开发的Ai智能问答系统。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。 那么如何搭建部署AI创作ChatGPT?小编这里写一个详细图文教程吧!…...
【高频面试题】 消息中间件
文章目录 1、RabbitMQ1.1 RabbitMQ-如何保证消息不丢失1.2 RabbitMQ消息的重复消费问题如何解决的1.3 RabbitMQ中死信交换机 ? (RabbitMQ延迟队列有了解过嘛)1.4 RabbitMQ如果有100万消息堆积在MQ , 如何解决(消息堆积怎么解决)1.5 RabbitMQ的高可用机制有了解过嘛 2、Kafka2.…...
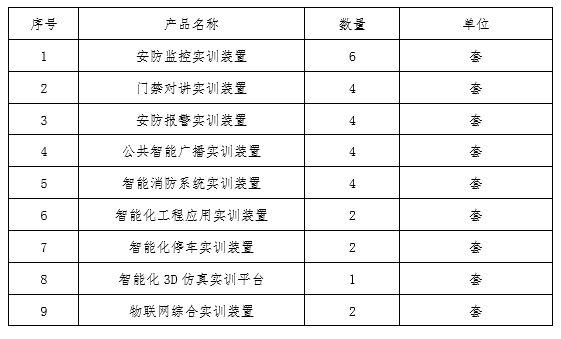
物联网智慧安防实训综合实训基地建设方案
一、系统概述 物联网智慧安防实训综合实训基地是一个为学生提供综合实践、培养技能的场所,专注于物联网技术与智慧安防应用的培训和实训。通过物联网智慧安防实训综合实训基地的建设和运营,学生可以在真实的环境中进行实践训练,提高其物联网技…...

openGauss学习笔记-44 openGauss 高级数据管理-存储过程
文章目录 openGauss学习笔记-44 openGauss 高级数据管理-存储过程44.1 语法格式44.2 参数说明44.3 示例 openGauss学习笔记-44 openGauss 高级数据管理-存储过程 存储过程是能够完成特定功能的SQL语句集。用户可以进行反复调用,从而减少SQL语句的重复编写数量&…...

【Linux】进程信号篇Ⅲ:可重入函数、volatile关键字、SIGCHLD信号
信号Ⅲ 🔗 接上篇七、可重入函数八、volatile 关键字九、SIGCHLD 信号 🔗 接上篇 👉🔗进程信号篇Ⅰ:信号的产生(signal、kill、raise、abort、alarm)、信号的保存(core dump&#x…...

排序算法:冒泡排序
冒泡排序是入门级的算法,但也有一些有趣的玩法。通常来说,冒泡排序有三种写法: 一边比较一边向后两两交换,将最大值 / 最小值冒泡到最后一位;经过优化的写法:使用一个变量记录当前轮次的比较是否发生过交换…...
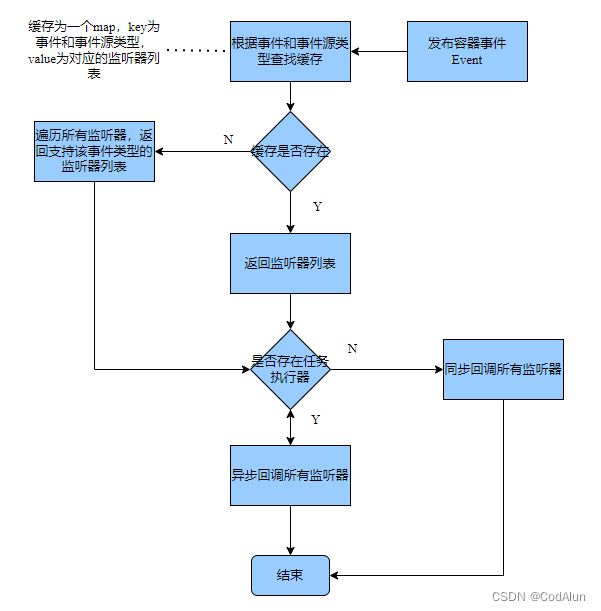
Spring事件监听源码解析
spring事件监听机制离不开容器IOC特性提供的支持,比如容器会自动创建事件发布器,自动识别用户注册的监听器并进行管理,在特定的事件发布后会找到对应的事件监听器并对其监听方法进行回调。Spring帮助用户屏蔽了关于事件监听机制背后的很多细节…...
Cpp学习——list的模拟实现
目录 一,实现list所需要包含的三个类 二,三个类的实现 1.list_node 2.list类 3.iterator_list类 三,功能实现 1.list类里的push_back() 2.iterator类里的运算符重载 3,list类里面的功能函数 1.insert(ÿ…...
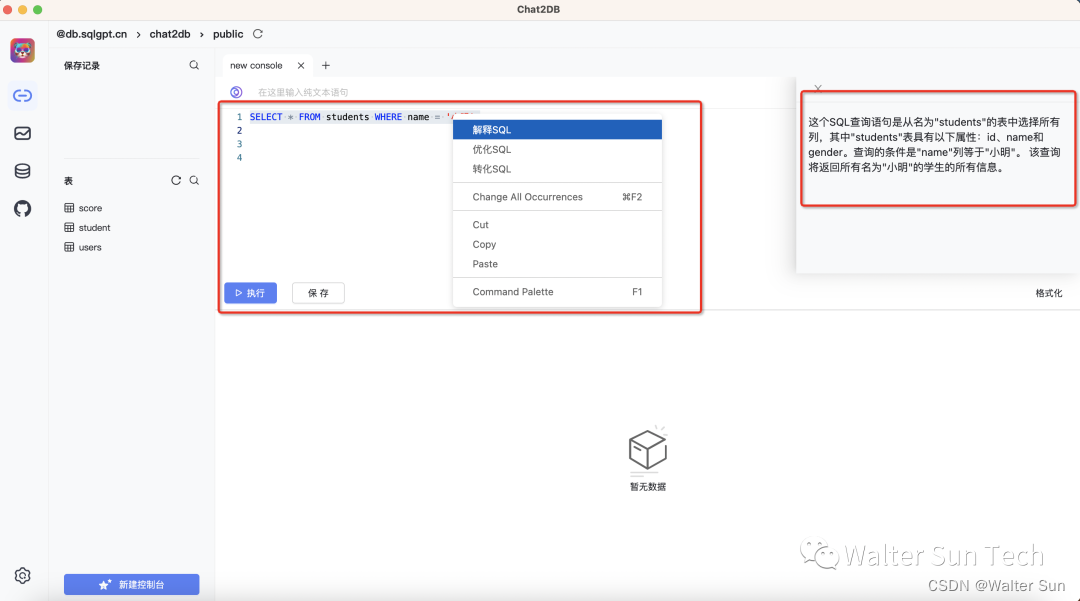
工具推荐:Chat2DB一款开源免费的多数据库客户端工具
文章首发地址 Chat2DB是一款开源免费的多数据库客户端工具,适用于Windows和Mac操作系统,可在本地安装使用,也可以部署到服务器端并通过Web页面进行访问。 相较于传统的数据库客户端软件如Navicat、DBeaver,Chat2DB具备了与AIGC…...
C语言刷题指南(二)
📙作者简介: 清水加冰,目前大二在读,正在学习C/C、Python、操作系统、数据库等。 📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。 欢迎点赞 👍…...
[C++11]
文章目录 1. 自动类型推导1.1 auto1.1.1 推导规则1.1.2 auto的限制1.1.3 auto的应用1.1.4 范围for 1.2 decltype1.2.1 推导规则1.2.2 decltype的应用 1.3 返回类型后置 2.可调用对象包装器、绑定器2.1 可调用对象包装器2.1.1 基本用法2.1.2 作为回调函数使用 2.2 绑定器 3. usi…...
【MySQL系列】--初识数据库
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...

Unity导入google.protobuf失败,无法找到google命名空间
问题: 1.刚开始把protobuf的文件夹直接从其他项目里(unity2021)里复制到unity(2020)版本,当时报错protobuf.dll的依赖项system.memory版本不对。 2.没有使用原来的protobuf文件了。使用vs2019的NuGet管理包来下载Google.Protobuf ,仍然报错找…...
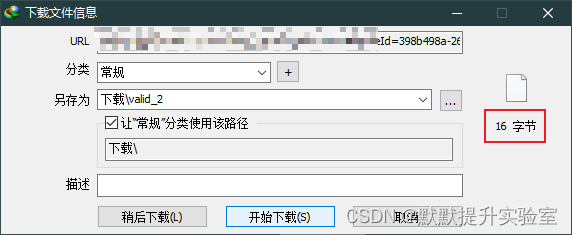
使用IDM下载视频出现“由于法律原因,IDM无法下载...
一、问题描述 由于法律原因,IDM无法下载..,如图: 二、原因分析 下载该IDM抓取的M3U8文件,查看其中的内容发现 : #EXT-X-KEY 字段已经写明了加密方式是AES-128,包含一个URI和IV值 #EXTM3U #EXT-X-VERSION:3 #EXT-X-TARGETDURATION:8 #EXT-X-MEDIA-SEQUENCE:0 #EXT-X-KEY:…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
