当前位置： 首页 > news >正文

使用线性回归模型优化权重：探索数据拟合的基础

news 2025/12/17 11:48:22

文章目录

  • 前言
  • 一、示例代码
  • 二、示例代码解读
    • 1.线性回归模型
    • 2.MSE损失函数
    • 3.优化过程
    • 4.结果解读
  • 总结

前言

在机器学习和数据科学中，线性回归是一种常见而重要的方法。本文将以一个简单的代码示例为基础，介绍线性回归的基本原理和应用。将使用Python和NumPy库来实现一个简单的线性回归模型和使用最小均方误差（MSE）损失函数来衡量模型的拟合准确性，并通过优化权重参数来提高模型的性能。

一、示例代码

import numpy as np
import matplotlib.pyplot as plt# 准备数据
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]w = 0.0  # 定义并初始化权重参数# 定义模型
def forward(x):return x*w# 定义损失函数
def loss(x, y):y_pred = forward(x)return (y_pred-y) * (y_pred-y)# 存放权重和损失值，保留在列表里面
w_list = []
mse_list = []# 生成0.0-4.0，步长值为0.1的序列
for w in np.arange(0.0, 4.1, 0.1):print('w=',w)l_sum = 0for x_val, y_val in zip(x_data, y_data):   # 将x_data和y_data进行组合成一个新的迭代器，相当于【(x_data【0】，y_data【0】)，（x_data【1】，y_data【1】）】y_pred_val = forward(x_val)  # 计算预测值loss_val = loss(x_val, y_val)  # 计算损失l_sum += loss_val  # 将这一轮中的损失值进行累加，用于计算平均损失值print('\t', x_val, y_val, y_pred_val, loss_val)print('MSE=', l_sum / 3)w_list.append(w)mse_list.append(l_sum / 3)# 在绘图中显示
plt.plot(w_list, mse_list)
plt.ylabel('loss')
plt.xlabel('w')
plt.show()

代码结果：

w= 0.01.0 2.0 0.0 4.02.0 4.0 0.0 16.03.0 6.0 0.0 36.0
MSE= 18.666666666666668
w= 0.11.0 2.0 0.1 3.612.0 4.0 0.2 14.443.0 6.0 0.30000000000000004 32.49
MSE= 16.846666666666668
w= 0.21.0 2.0 0.2 3.242.0 4.0 0.4 12.963.0 6.0 0.6000000000000001 29.160000000000004
MSE= 15.120000000000003
w= 0.300000000000000041.0 2.0 0.30000000000000004 2.88999999999999972.0 4.0 0.6000000000000001 11.5599999999999993.0 6.0 0.9000000000000001 26.009999999999998
MSE= 13.486666666666665
w= 0.41.0 2.0 0.4 2.56000000000000052.0 4.0 0.8 10.2400000000000023.0 6.0 1.2000000000000002 23.04
MSE= 11.946666666666667
w= 0.51.0 2.0 0.5 2.252.0 4.0 1.0 9.03.0 6.0 1.5 20.25
MSE= 10.5
w= 0.60000000000000011.0 2.0 0.6000000000000001 1.95999999999999972.0 4.0 1.2000000000000002 7.8399999999999993.0 6.0 1.8000000000000003 17.639999999999993
MSE= 9.146666666666663
w= 0.70000000000000011.0 2.0 0.7000000000000001 1.68999999999999952.0 4.0 1.4000000000000001 6.7599999999999983.0 6.0 2.1 15.209999999999999
MSE= 7.886666666666666
w= 0.81.0 2.0 0.8 1.442.0 4.0 1.6 5.763.0 6.0 2.4000000000000004 12.959999999999997
MSE= 6.719999999999999
w= 0.91.0 2.0 0.9 1.21000000000000022.0 4.0 1.8 4.8400000000000013.0 6.0 2.7 10.889999999999999
MSE= 5.646666666666666
w= 1.01.0 2.0 1.0 1.02.0 4.0 2.0 4.03.0 6.0 3.0 9.0
MSE= 4.666666666666667
w= 1.11.0 2.0 1.1 0.80999999999999982.0 4.0 2.2 3.23999999999999933.0 6.0 3.3000000000000003 7.289999999999998
MSE= 3.779999999999999
w= 1.20000000000000021.0 2.0 1.2000000000000002 0.63999999999999972.0 4.0 2.4000000000000004 2.55999999999999873.0 6.0 3.6000000000000005 5.759999999999997
MSE= 2.986666666666665
w= 1.31.0 2.0 1.3 0.489999999999999942.0 4.0 2.6 1.95999999999999973.0 6.0 3.9000000000000004 4.409999999999998
MSE= 2.2866666666666657
w= 1.40000000000000011.0 2.0 1.4000000000000001 0.35999999999999982.0 4.0 2.8000000000000003 1.43999999999999933.0 6.0 4.2 3.2399999999999993
MSE= 1.6799999999999995
w= 1.51.0 2.0 1.5 0.252.0 4.0 3.0 1.03.0 6.0 4.5 2.25
MSE= 1.1666666666666667
w= 1.61.0 2.0 1.6 0.159999999999999922.0 4.0 3.2 0.63999999999999973.0 6.0 4.800000000000001 1.4399999999999984
MSE= 0.746666666666666
w= 1.70000000000000021.0 2.0 1.7000000000000002 0.08999999999999992.0 4.0 3.4000000000000004 0.35999999999999963.0 6.0 5.1000000000000005 0.809999999999999
MSE= 0.4199999999999995
w= 1.81.0 2.0 1.8 0.039999999999999982.0 4.0 3.6 0.159999999999999923.0 6.0 5.4 0.3599999999999996
MSE= 0.1866666666666665
w= 1.90000000000000011.0 2.0 1.9000000000000001 0.0099999999999999742.0 4.0 3.8000000000000003 0.03999999999999993.0 6.0 5.7 0.0899999999999999
MSE= 0.046666666666666586
w= 2.01.0 2.0 2.0 0.02.0 4.0 4.0 0.03.0 6.0 6.0 0.0
MSE= 0.0
w= 2.11.0 2.0 2.1 0.0100000000000000182.0 4.0 4.2 0.040000000000000073.0 6.0 6.300000000000001 0.09000000000000043
MSE= 0.046666666666666835
w= 2.21.0 2.0 2.2 0.040000000000000072.0 4.0 4.4 0.160000000000000283.0 6.0 6.6000000000000005 0.36000000000000065
MSE= 0.18666666666666698
w= 2.30000000000000031.0 2.0 2.3000000000000003 0.090000000000000162.0 4.0 4.6000000000000005 0.360000000000000653.0 6.0 6.9 0.8100000000000006
MSE= 0.42000000000000054
w= 2.40000000000000041.0 2.0 2.4000000000000004 0.160000000000000282.0 4.0 4.800000000000001 0.64000000000000113.0 6.0 7.200000000000001 1.4400000000000026
MSE= 0.7466666666666679
w= 2.51.0 2.0 2.5 0.252.0 4.0 5.0 1.03.0 6.0 7.5 2.25
MSE= 1.1666666666666667
w= 2.61.0 2.0 2.6 0.36000000000000012.0 4.0 5.2 1.44000000000000043.0 6.0 7.800000000000001 3.2400000000000024
MSE= 1.6800000000000008
w= 2.71.0 2.0 2.7 0.490000000000000272.0 4.0 5.4 1.9600000000000013.0 6.0 8.100000000000001 4.410000000000006
MSE= 2.2866666666666693
w= 2.80000000000000031.0 2.0 2.8000000000000003 0.64000000000000052.0 4.0 5.6000000000000005 2.5600000000000023.0 6.0 8.4 5.760000000000002
MSE= 2.986666666666668
w= 2.90000000000000041.0 2.0 2.9000000000000004 0.81000000000000062.0 4.0 5.800000000000001 3.24000000000000243.0 6.0 8.700000000000001 7.290000000000005
MSE= 3.780000000000003
w= 3.01.0 2.0 3.0 1.02.0 4.0 6.0 4.03.0 6.0 9.0 9.0
MSE= 4.666666666666667
w= 3.11.0 2.0 3.1 1.21000000000000022.0 4.0 6.2 4.8400000000000013.0 6.0 9.3 10.890000000000004
MSE= 5.646666666666668
w= 3.21.0 2.0 3.2 1.44000000000000042.0 4.0 6.4 5.7600000000000023.0 6.0 9.600000000000001 12.96000000000001
MSE= 6.720000000000003
w= 3.30000000000000031.0 2.0 3.3000000000000003 1.69000000000000062.0 4.0 6.6000000000000005 6.76000000000000253.0 6.0 9.9 15.210000000000003
MSE= 7.886666666666668
w= 3.40000000000000041.0 2.0 3.4000000000000004 1.9600000000000012.0 4.0 6.800000000000001 7.8400000000000043.0 6.0 10.200000000000001 17.640000000000008
MSE= 9.14666666666667
w= 3.51.0 2.0 3.5 2.252.0 4.0 7.0 9.03.0 6.0 10.5 20.25
MSE= 10.5
w= 3.61.0 2.0 3.6 2.56000000000000052.0 4.0 7.2 10.2400000000000023.0 6.0 10.8 23.040000000000006
MSE= 11.94666666666667
w= 3.71.0 2.0 3.7 2.89000000000000062.0 4.0 7.4 11.5600000000000023.0 6.0 11.100000000000001 26.010000000000016
MSE= 13.486666666666673
w= 3.80000000000000031.0 2.0 3.8000000000000003 3.2400000000000012.0 4.0 7.6000000000000005 12.9600000000000043.0 6.0 11.4 29.160000000000004
MSE= 15.120000000000005
w= 3.90000000000000041.0 2.0 3.9000000000000004 3.6100000000000012.0 4.0 7.800000000000001 14.4400000000000053.0 6.0 11.700000000000001 32.49000000000001
MSE= 16.84666666666667
w= 4.01.0 2.0 4.0 4.02.0 4.0 8.0 16.03.0 6.0 12.0 36.0
MSE= 18.666666666666668

可以显而易见

w= 2.01.0 2.0 2.0 0.02.0 4.0 4.0 0.03.0 6.0 6.0 0.0
MSE= 0.0

当w=2时，mse=0,即我们需要的最优模型为y=2x
绘图显示如下：
在这里插入图片描述
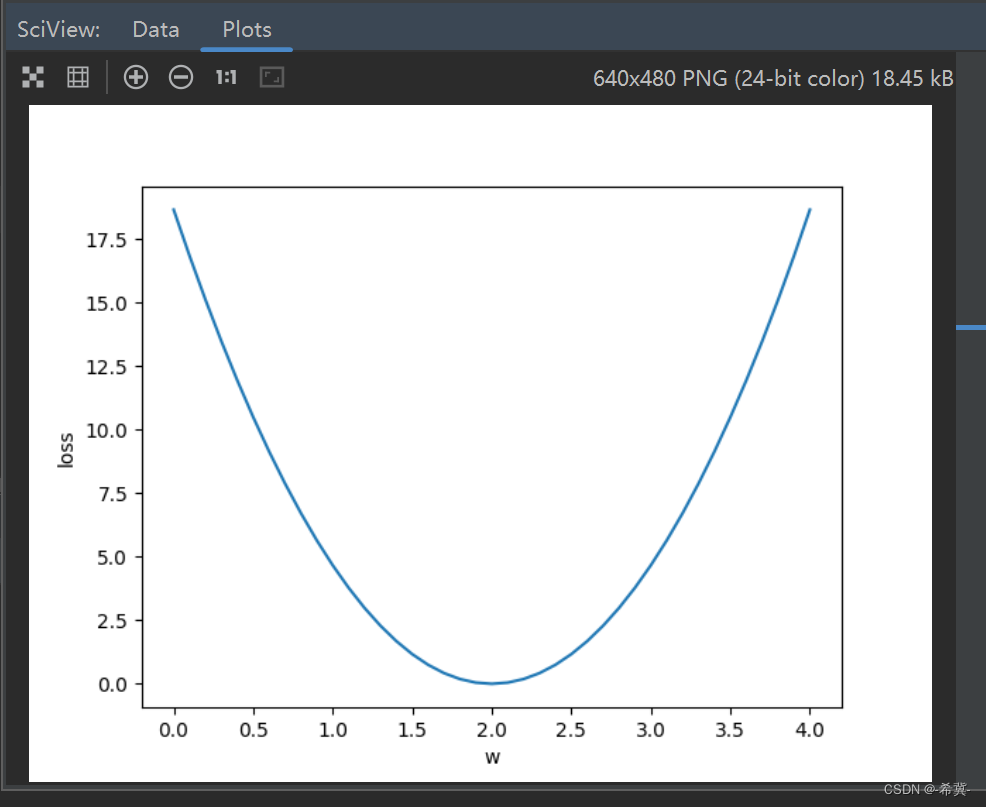
从图上也可以直观显示w=2时模型为优。

二、示例代码解读

1.线性回归模型

在这个示例代码中，定义了一个简单的线性回归模型，其中输入特征与权重参数进行线性组合，得到预测结果。这个模型的数学表示就是y=w*x，其中y是预测结果，w是权重参数，x是输入特征。

2.MSE损失函数

使用最小均方误差MSE作为损失函数来衡量模型的拟合准确性。MSE计算预测值与真实值之差的平方，并求平均值。在这段代码中，定义了一个损失函数loss（x,y）,其中x和y分别表示输入特征和真实值。该函数通过调用前向传播函数forward(x)得到预测值，并在计算损失时使用了MSE公式。

3.优化过程

现在，我们探讨优化过程。在代码中，我们使用了np.arange生成0.0到4.0步长为0.1的一系列权重值作为迭代的候选权重参数，然后，通过遍历数据集中样本，计算每个权重值对应的平均损失。循环迭代过程中，存储权重和损失值的列表w_list和mse_list,最终使用matplotlib.pyplot绘制出权重与平均损失的关系图。

4.结果解读

通过绘制的图像，我们可以观察到权重与平均损失之间的关系。对于不同的权重取值，平均损失会有所变化。我们的目的是寻找使损失最小化的最优权重。通过不断调整权重参数，我们可以优化模型的拟合效果，使得预测结果与真实值更接近。

关于文章中zip(）函数用法，可以参看我的这一篇文章：Python中的zip函数：合并和解压可迭代对象的利器。

总结

通过观察权重与平均损失的关系图，我们可以找到使损失最小化的最优权重。这个示例代码展示了如何利用线性回归模型和MSE损失函数来优化权重参数，以实现更好的数据拟合。线性回归是机器学习中最基础的模型之一，理解其原理和应用对于理解其他回归算法和数据拟合技术非常重要。通过学习和应用这些基本概念，我们可以更好地处理和分析实际问题，并为数据提供准确的预测和解释。

相关文章：

使用线性回归模型优化权重：探索数据拟合的基础

文章目录 前言一、示例代码二、示例代码解读1.线性回归模型2.MSE损失函数3.优化过程4.结果解读 总结 前言 在机器学习和数据科学中，线性回归是一种常见而重要的方法。本文将以一个简单的代码示例为基础，介绍线性回归的基本原理和应用。将使用Python和Nu…...

编程日记 2023/8/20 9:20:22

亿级短视频，如何架构？

说在前面 在尼恩的（50）读者社群中，经常指导大家面试架构，拿高端offer。 前几天，指导一个年薪100W小伙伴，拿到字节面试邀请。 遇到一个 非常、非常高频的一个面试题，但是很不好回答&#xff0…...

编程日记 2023/8/20 9:19:21

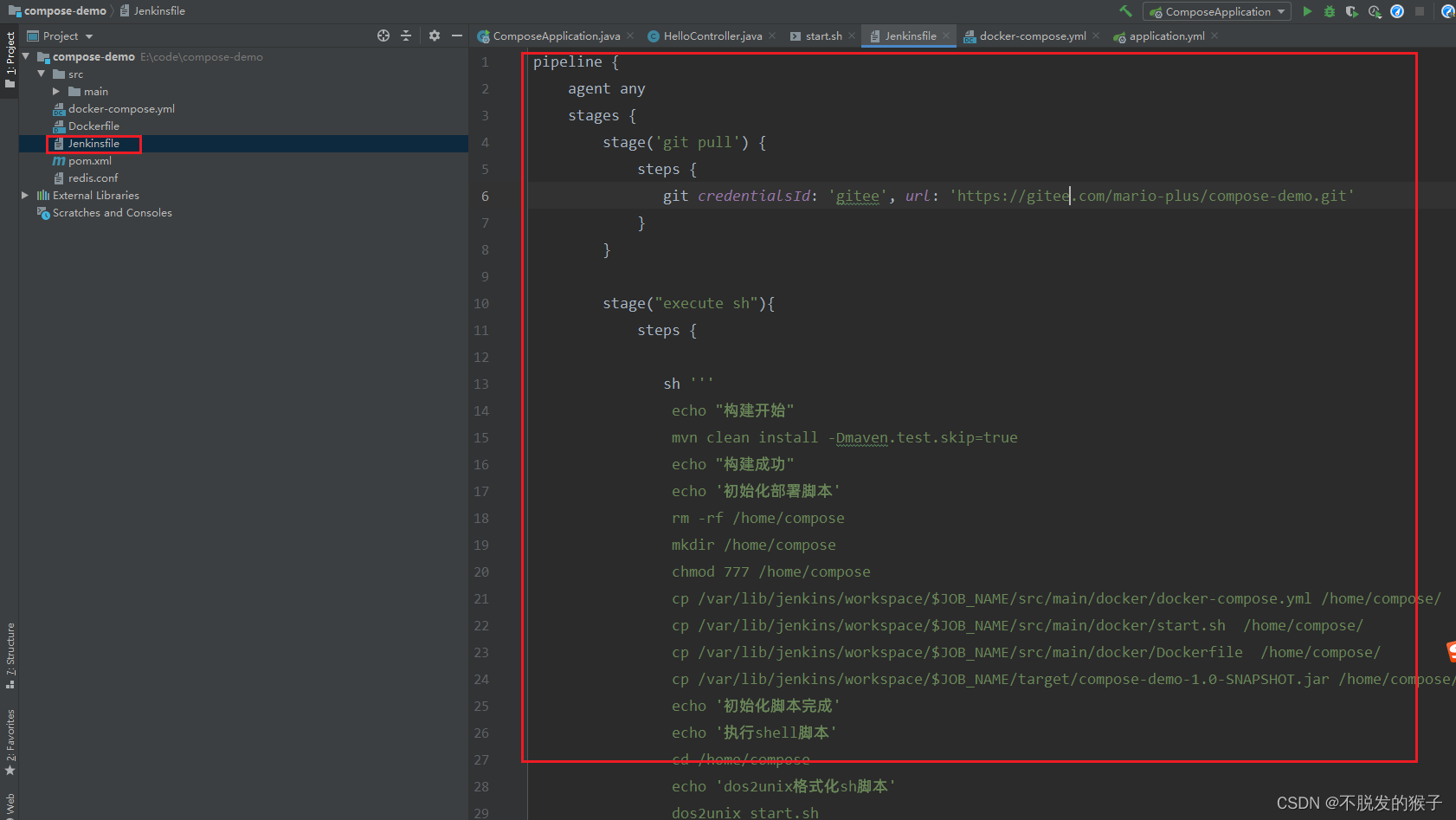
jenkins pipeline方式一键部署github项目

上篇：jenkins一键部署github项目 该篇使用jenkins pipeline-script一键部署，且介绍pipeline-scm jenkins环境配置 前言：按照上篇创建pipeline任务，结果报mvn，jdk环境不存在，就很疑惑，然后配置全…...

编程日记 2023/8/20 9:18:20

Vue 项目搭建

环境配置 1. 安装node.js 官网：nodejs（推荐 v10 以上） 官网：npm 是什么？ 由于vue的安装与创建依赖node.js（JavaScript的运行环境）里的npm（包管理和分发工具）&#xff…...

编程日记 2023/8/20 9:17:16

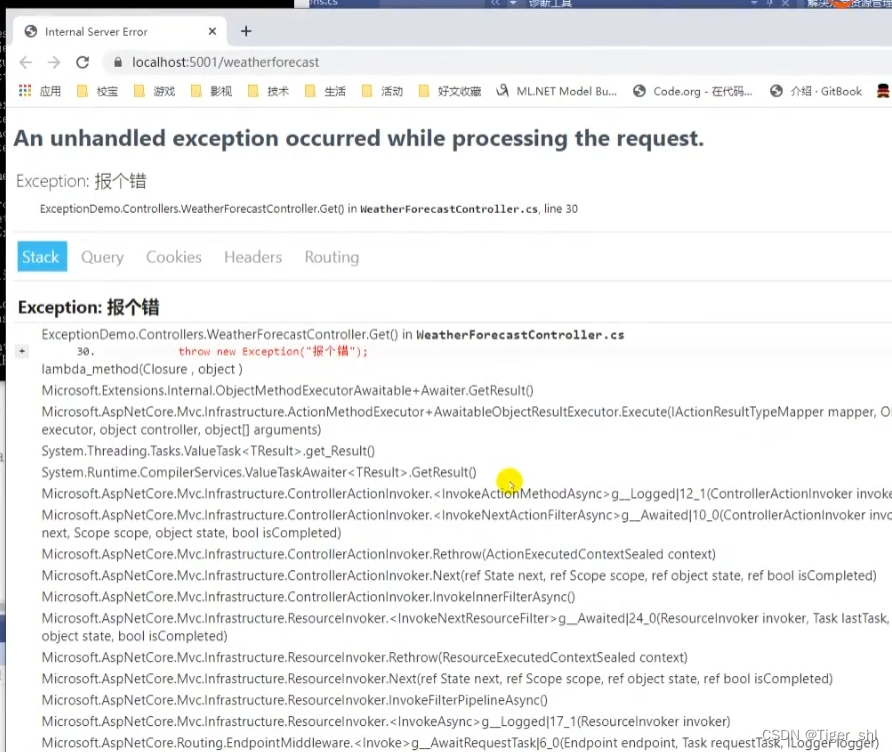
【NetCore】09-中间件

文章目录 中间件：掌控请求处理过程的关键1. 中间件1.1 中间件工作原理1.2 中间件核心对象 2.异常处理中间件:区分真异常和逻辑异常2.1 处理异常的方式2.1.1 日常错误处理--定义错误页的方法2.1.2 使用代理方法处理异常2.1.3 异常过滤器 IExceptionFilter2.1.4 特性过…...

编程日记 2023/8/20 9:16:15

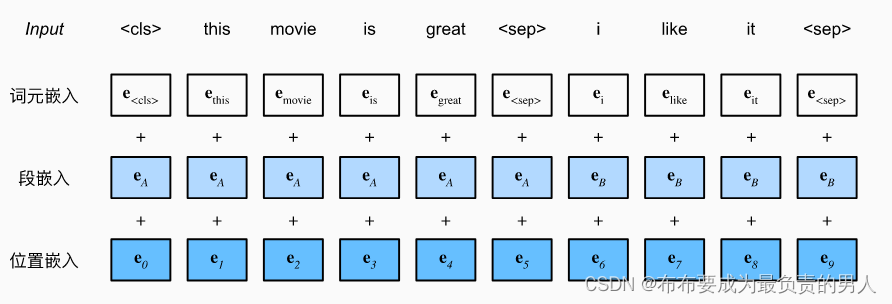
机器学习深度学习——BERT（来自transformer的双向编码器表示）

👨‍🎓作者简介：一位即将上大四，正专攻机器学习的保研er 🌌上期文章：机器学习&&深度学习——transformer（机器翻译的再实现） 📚订阅专栏：机器学习&am…...

编程日记 2023/8/20 9:15:14

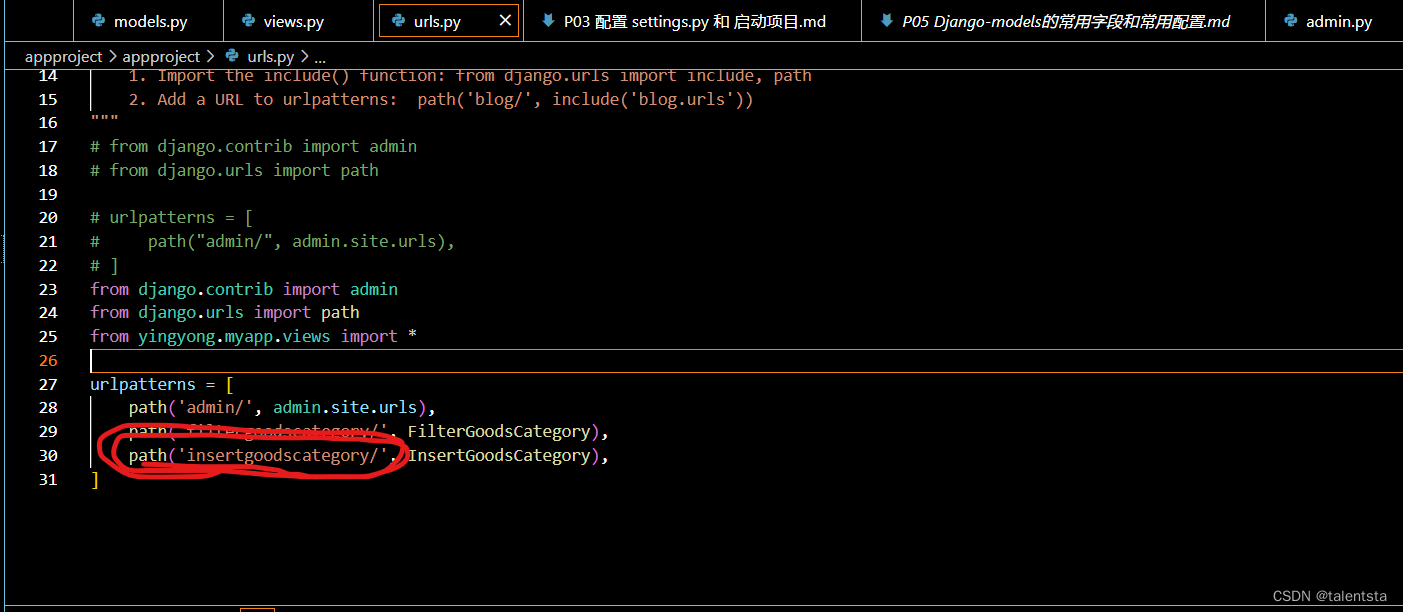
Datawhale Django后端开发入门 Vscode TASK02 Admin管理员、外键的使用

一.Admin管理员的使用 1、启动django服务 使用创建管理员之前，一定要先启动django服务，虽然TASK01和TASK02是分开的，但是进行第二个流程的时候记得先启动django服务，注意此时是在你的项目文件夹下启动的，时刻注意要执…...

编程日记 2023/8/20 9:14:13

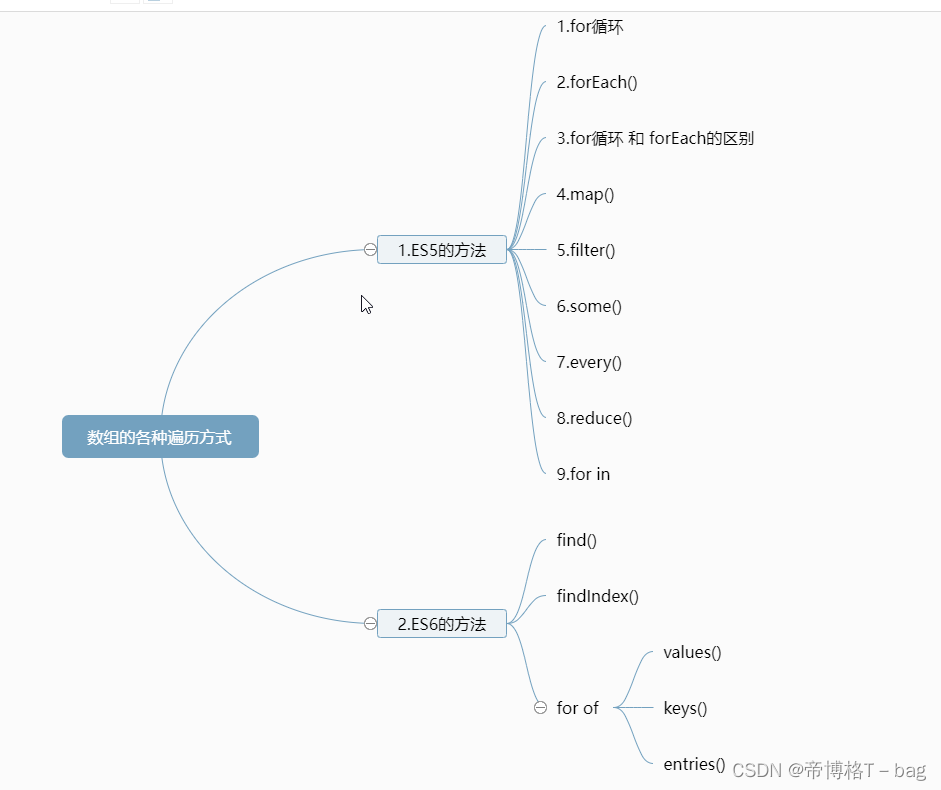
【ES5和ES6】数组遍历的各种方法集合

一、ES5的方法 1.for循环 let arr [1, 2, 3] for (let i 0; i < arr.length; i) {console.log(arr[i]) } // 1 // 2 // 32.forEach() 特点&#xff1a; 没有返回值&#xff0c;只是针对每个元素调用func三个参数&#xff1a;item, index, arr &#xff1b;当前项&#…...

编程日记 2023/8/20 9:13:12

学科在线教育元宇宙VR虚拟仿真平台落实更高质量的交互学习

为推动教育数字化&#xff0c;建设全民终身学习的学习型社会、学习型大国&#xff0c;元宇宙企业深圳华锐视点深度融合VR虚拟现实、数字孪生、云计算和三维建模等技术&#xff0c;搭建教育元宇宙平台&#xff0c;为学生提供更加沉浸式的学习体验&#xff0c;提高学习效果和兴趣…...

编程日记 2023/8/20 9:12:10

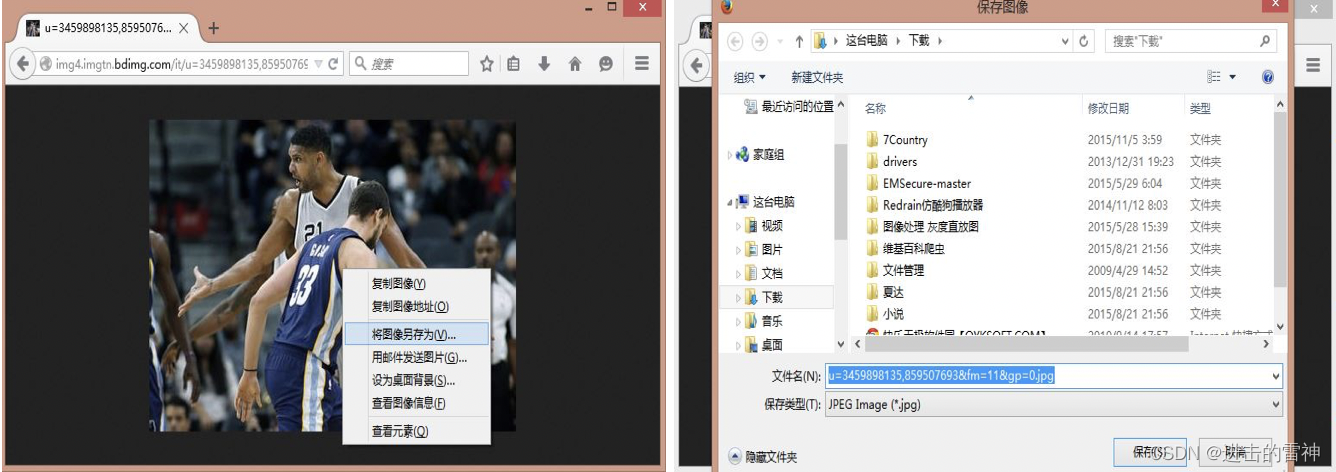
[python爬虫] 爬取图片无法打开或已损坏的简单探讨

本文主要针对python使用urlretrieve或urlopen下载百度、搜狗、googto&#xff08;谷歌镜像&#xff09;等图片时&#xff0c;出现"无法打开图片或已损坏"的问题&#xff0c;作者对它进行简单的探讨。同时&#xff0c;作者将进一步帮你巩固selenium自动化操作和urllib…...

编程日记 2023/8/20 9:11:07

vue项目预览pdf功能（解决动态文字无法显示的问题）

最近&#xff0c;因为公司项目需要预览pdf的功能&#xff0c;开始的时候找了市面上的一些pdf插件&#xff0c;都能用&#xff0c;但是&#xff0c;后面因为pdf变成了需要根据内容进行变化的&#xff0c;然后&#xff0c;就出现了需要动态生成的文字不显示了。换了好多好多的插件…...

编程日记 2023/8/20 9:10:06

vue3 样式穿透:deep不生效

初学vue3&#xff0c;今天需要修改el-input组件的属性&#xff08;去掉border和文字居右&#xff09; 网上搜了一下&#xff0c;大致都是采用:deep 样式穿透来修改el-input的属性 <div class"input-container"><el-input placeholder"请输入111&qu…...

编程日记 2023/8/20 9:09:05

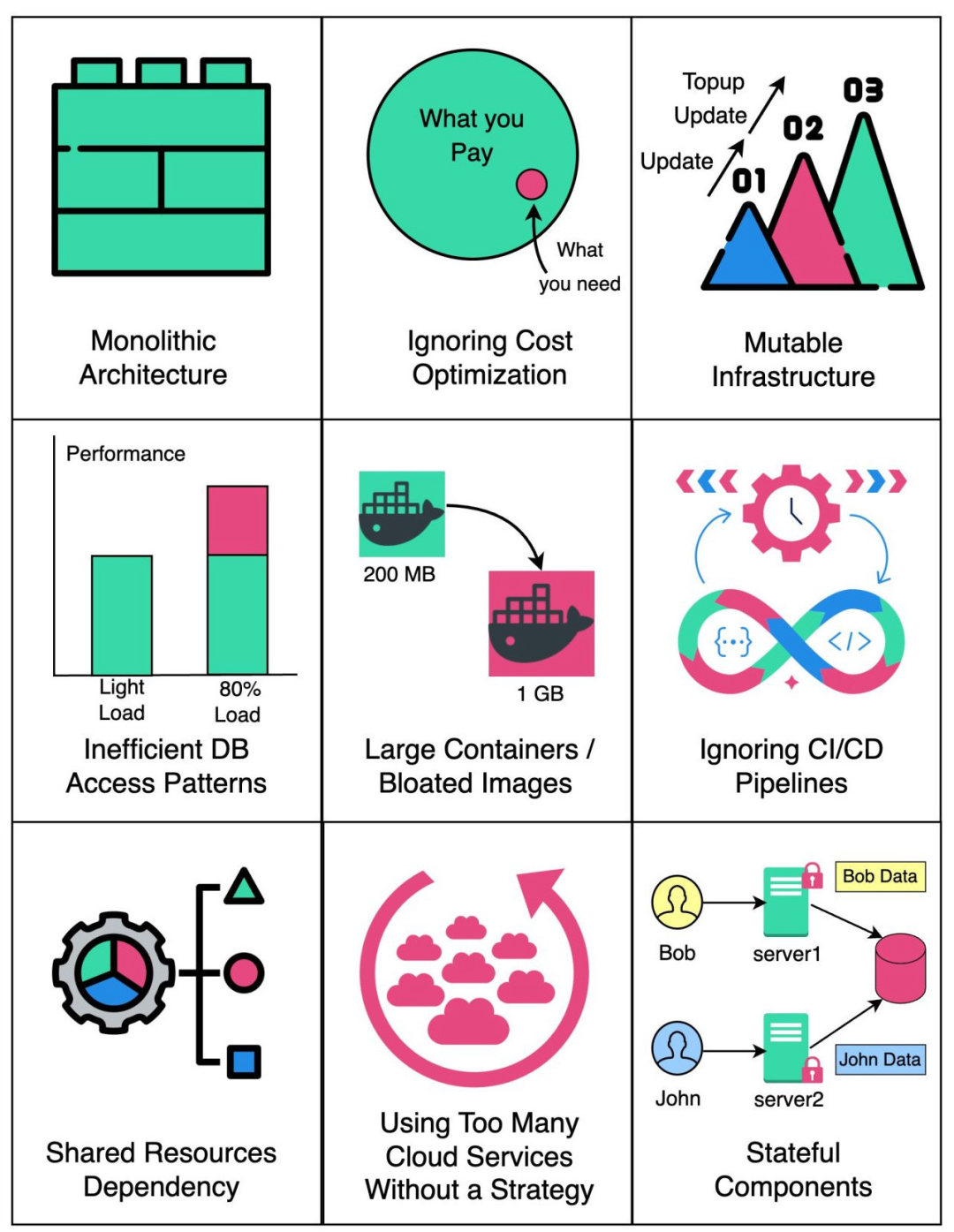
云原生反模式

通过了解这些反模式并遵循云原生最佳实践&#xff0c;您可以设计、构建和运营更加强大、可扩展和成本效益高的云原生应用程序。 1.单体架构&#xff1a;在云上运行一个大而紧密耦合的应用程序&#xff0c;妨碍了可扩展性和敏捷性。2.忽略成本优化&#xff1a;云服务可能昂贵&am…...

编程日记 2023/8/20 9:08:02

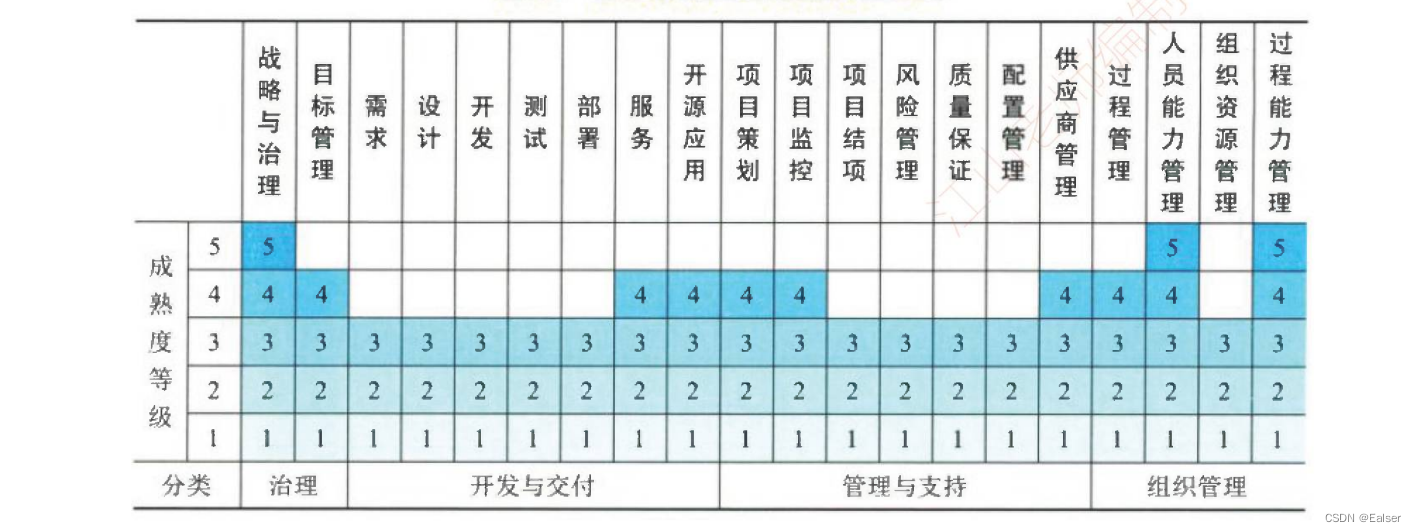
【2023年11月第四版教材】《第5章-信息系统工程（合集篇）》

《第5章-信息系统工程&#xff08;合集篇&#xff09;》 章节说明1 软件工程1.1 架构设计1.2 需求分析1.3 软件设计1.4 软件实现&#xff3b;补充第三版教材内容&#xff3d; 1.5 部署交付 2 数据工程2.1 数据建模2.2 数据标准化2.3 数据运维2.4 数据开发利用2.5 数据库安全 3 …...

编程日记 2023/8/20 9:07:01

【qiankun】微前端在项目中的具体使用

1、安装qiankun npm install qiankun --save2、主应用中注册和配置qiankun 在主应用的入口文件main.ts中&#xff0c;引入qiankun的注册方法&#xff1a; import { registerMicroApps, start } from qiankun;创建一个数组&#xff0c;用于配置子应用的相关信息。每个子应用都…...

编程日记 2023/8/20 9:06:00

云安全与多云环境管理：讨论在云计算和多云环境下如何保护数据、应用程序和基础设施的安全

随着云计算和多云环境的广泛应用&#xff0c;企业正面临着数据、应用程序和基础设施安全的新挑战。在这个数字化时代&#xff0c;保护敏感信息和业务运作的连续性变得尤为重要。本文将深入探讨在云计算和多云环境下如何有效地保护数据、应用程序和基础设施的安全。 章节一&…...

编程日记 2023/8/20 9:04:59

npm install ffi各种失败，换命令npm i ffi-napi成功

网上各种帖子安装ffi&#xff0c;基本上到了windows build tools这里会卡住。 使用命令npm install --global --production windows-build-tools 安装报错信息如下&#xff1a; PS E:\codes\nodejsPath\tcpTest> npm install --global --production windows-build-tools …...

编程日记 2023/8/20 9:03:58

0.flink学习资料

论文&#xff1a; &#xff08;1&#xff09;google dataflow model 下载链接&#xff1a;p1792-Akidau.pdf (vldb.org) Akidau T, Bradshaw R, Chambers C, et al. The dataflow model: a practical approach to balancing correctness, latency, and cost in massive-scal…...

编程日记 2023/8/20 9:02:56

C语言：字符函数和字符串函数

往期文章 C语言&#xff1a;初识C语言C语言&#xff1a;分支语句和循环语句C语言&#xff1a;函数C语言&#xff1a;数组C语言&#xff1a;操作符详解C语言&#xff1a;指针详解C语言&#xff1a;结构体C语言&#xff1a;数据的存储 目录 往期文章前言1. 函数介绍1.1 strlen1.…...

编程日记 2023/8/20 9:01:54

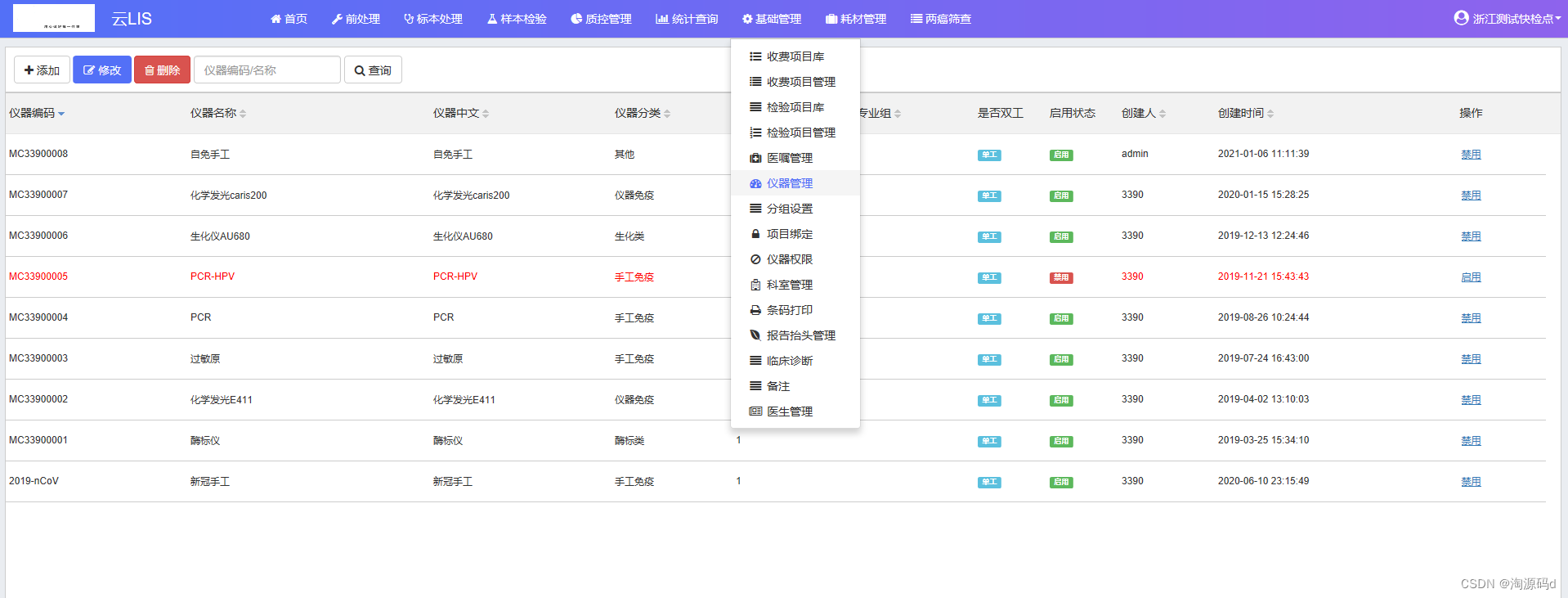
基于.Net Core开发的医疗信息LIS系统源码

SaaS模式.Net Core版云LIS系统源码 医疗信息LIS系统是专为医院检验科设计的一套实验室信息管理系统&#xff0c;能将实验仪器与计算机组成网络&#xff0c;使病人样品登录、实验数据存取、报告审核、打印分发&#xff0c;实验数据统计分析等繁杂的操作过程实现了智能化、自动化…...

编程日记 2023/8/20 9:00:52

wordpress后台更新后 前端没变化的解决方法

使用siteground主机的wordpress网站&#xff0c;会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后&#xff0c;网站没有变化的情况。 不熟悉siteground主机的新手&#xff0c;遇到这个问题&#xff0c;就很抓狂&#xff0c;明明是哪都没操作错误&#x…...

编程新知 2025/12/16 5:34:39

调用支付宝接口响应40004 SYSTEM_ERROR问题排查

在对接支付宝API的时候&#xff0c;遇到了一些问题&#xff0c;记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

编程新知 2025/12/10 15:30:17

大话软工笔记—需求分析概述

需求分析&#xff0c;就是要对需求调研收集到的资料信息逐个地进行拆分、研究&#xff0c;从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要&#xff0c;后续设计的依据主要来自于需求分析的成果&#xff0c;包括: 项目的目的…...

编程新知 2025/12/11 23:45:42

Cinnamon修改面板小工具图标

Cinnamon开始菜单-CSDN博客 设置模块都是做好的&#xff0c;比GNOME简单得多&#xff01; 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

编程新知 2025/12/14 17:38:32

九天毕昇深度学习平台 | 如何安装库？

pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子&#xff1a; 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

编程新知 2025/12/10 1:16:05

让回归模型不再被异常值“带跑偏“，MSE和Cauchy损失函数在噪声数据环境下的实战对比

在机器学习的回归分析中&#xff0c;损失函数的选择对模型性能具有决定性影响。均方误差&#xff08;MSE&#xff09;作为经典的损失函数&#xff0c;在处理干净数据时表现优异&#xff0c;但在面对包含异常值的噪声数据时&#xff0c;其对大误差的二次惩罚机制往往导致模型参数…...

编程新知 2025/12/12 18:44:23

论文笔记——相干体技术在裂缝预测中的应用研究

目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术&#xff1a;基于互相关的相干体技术&#xff08;Correlation&#xff09;第二代相干体技术&#xff1a;基于相似的相干体技术&#xff08;Semblance&#xff09;基于多道相似的相干体…...

编程新知 2025/12/12 20:26:01

MFC 抛体运动模拟：常见问题解决与界面美化

在 MFC 中开发抛体运动模拟程序时，我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点，详细解析原因并提供解决方案，同时兼顾界面美化，让模拟效果更专业、更高效。 问题一：历史轨迹与小球残影残留 现象 小球运动后，历史位置的 “残影”…...

编程新知 2025/12/11 6:17:00

云原生安全实战：API网关Kong的鉴权与限流详解

&#x1f525;「炎码工坊」技术弹药已装填&#xff01; 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关&#xff08;API Gateway&#xff09; API网关是微服务架构中的核心组件&#xff0c;负责统一管理所有API的流量入口。它像一座…...

编程新知 2025/12/11 6:18:53

django blank 与 null的区别

1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是&#xff0c;要注意以下几点&#xff1a; Django的表单验证与null无关&#xff1a;null参数控制的是数据库层面字段是否可以为NULL&#xff0c;而blank参数控制的是Django表单验证时字…...

编程新知 2025/7/7 3:34:13