数据在内存中的存储(deeper)
数据在内存中的存储(deeper)
- 一.数据类型的详细介绍
- 二.整形在内存中的存储
- 三.浮点型在内存中的存储
一.数据类型的详细介绍
类型的意义:
- 使用这个类型开辟内存空间的大小(大小决定了使用范围)
- 如何看待内存空间的视角
(1)整形
char
unsigned char
signed char
short
unsigned short [int]
signed short [int]
int
unsigned int
signed int
long
unsigned long [int]
signed long [int]
(2)浮点型
float
double
(3)构造类型
> 数组类型
> 结构体类型 struct
> 枚举类型 enum
> 联合类型 union
(4)指针类型
int *pi;
char *pc;
float* pf;
void* pv;
(5)空类型
void 表示空类型(无类型)
通常应用于函数的返回类型、函数的参数、指针类型
二.整形在内存中的存储
(1)原码.反码.补码
三种表示方法均有符号位和数值位两部分,符号位都是用0表示‘正’,用1表示‘负’,数值位正数的原反补都相同,负整数的原反补各不相同
原码:直接将数值按照正负数的形式翻译成二进制就可以得到原码
反码:将原码的符号位不变,其他位按位取反就可以得到反码
补码:反码+1就得到补码
对于整形来说:数据存放内存中其实存放的是补码
为什么呢?
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统
一处理;同时,加法和减法也可以统一处理(CPU只有加法器)此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路
我们看看在内存中的存储:
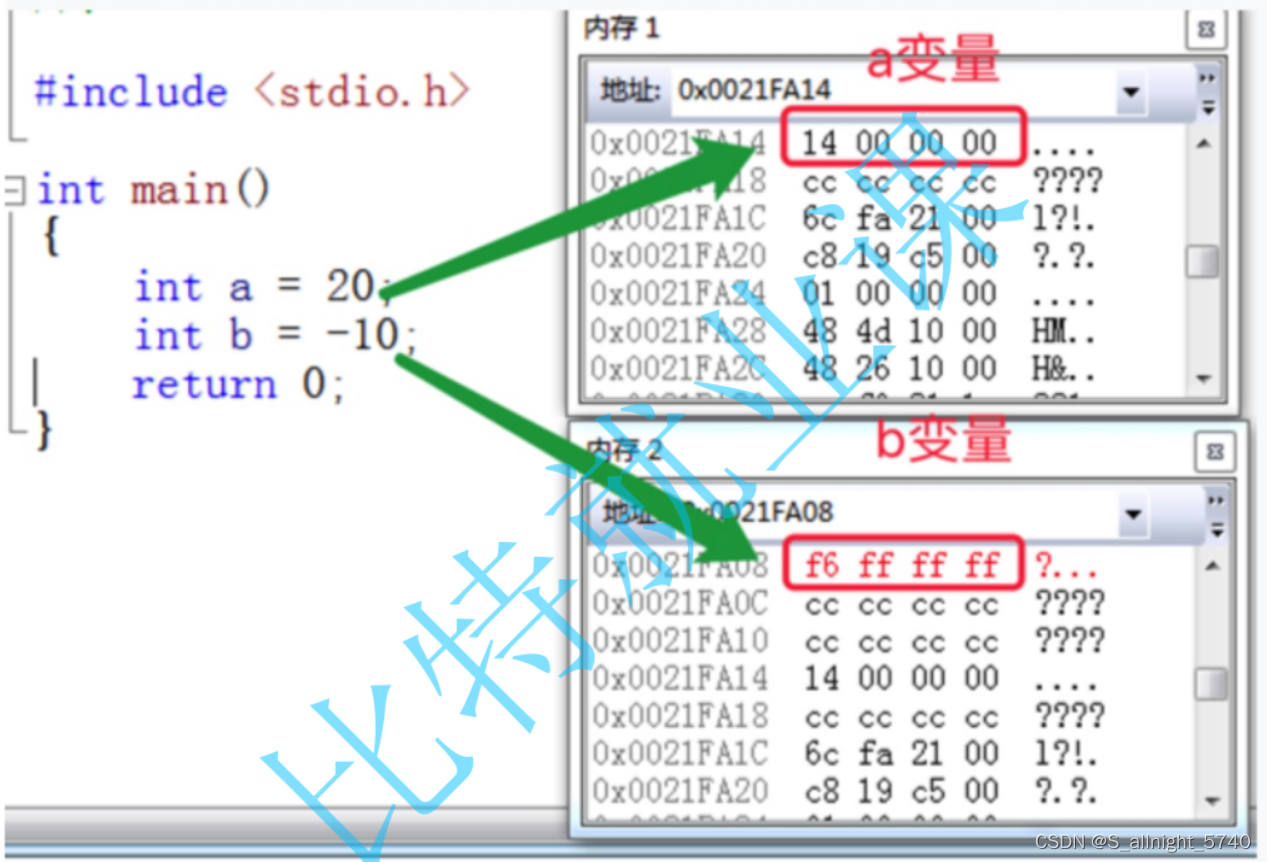
可以看到对于a和b分别存储的是补码,但是我们发现顺序有点不对劲,下面来解释一下原因
(2)大小端介绍
大端:是指数据的低位保存在内存的高地址,而数据的高位保存在内存的低地址中
小端:是指数据的低位保存在内存的低地址,而数据的高位保存在内存的高地址中
下面来设计一个小程序来判断当前机器的字节序吧!
#include <stdio.h>
int check_sys()
{int i = 1;return (*(char *)&i);
}
int main()
{int ret = check_sys();if(ret == 1){printf("小端\n");}else{printf("大端\n");}return 0;
}
三.浮点型在内存中的存储
一个浮点数存储的例子来引入话题吧:
int main()
{int n = 9;float *pFloat = (float *)&n;printf("n的值为:%d\n",n);printf("*pFloat的值为:%f\n",*pFloat);*pFloat = 9.0;printf("num的值为:%d\n",n);printf("*pFloat的值为:%f\n",*pFloat);return 0;
}

num 和 *pFloat 在内存中明明是同一个数,为什么浮点数和整数的解读结果会差别这么大?要理解这个结果,一定要搞懂浮点数在计算机内部的表示方法,详细解读:
根据IEEE,任意一个二进制浮点数V可以表示成下面的形式:
~(-1)^SM2*E
~ (-1)^S表示符号位,当S=0,V为正数;当S=1,V为负数
~ M表示有效数字,大于等于1,小于2
~ 2^E表示指数位
举例来说:
十进制的5.0,写成二进制是 101.0 ,相当于 1.01×2^2 。
那么,按照上面V的格式,可以得出S=0,M=1.01,E=2
十进制的-5.0,写成二进制是 -101.0 ,相当于 -1.01×2^2,那么,S=1,M=1.01,E=2
IEEE 754规定:
对于32位的浮点数,最高的1位是符号位s,接着的8位是指数E,剩下的23位为有效数字M

对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M
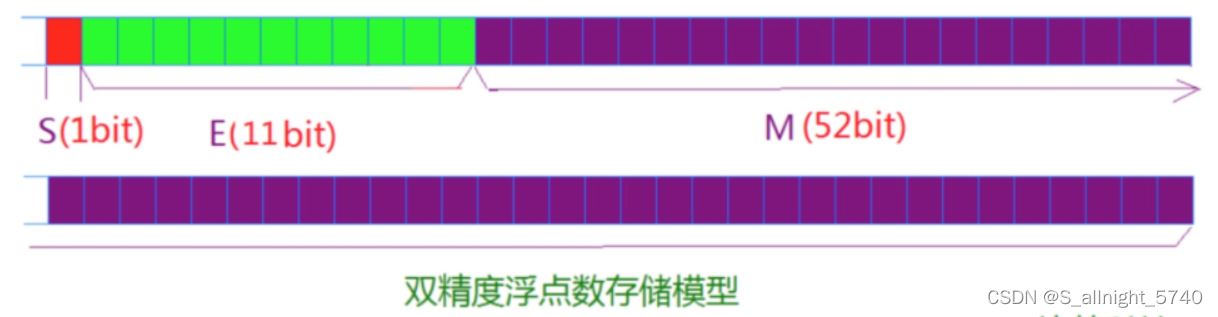
IEEE 754对有效数字M和指数E,还有一些特别规定,1≤M<2 ,也就是说,M可以写成 1.xxxxxx 的形式,其中xxxxxx表示小数部分,IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx部分,比如保存1.01的时候,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。以32位,浮点数为例,留给M只有23位,将第一位的1舍去以后,等于可以保存24位有效数字
至于指数E,情况就比较复杂,首先,E为一个无符号整数(unsigned int)这意味着,如果E为8位,它的取值范围为0~255;如果E为11位,它的取值范围为0 ~ 2047,但是,我们知道,科学计数法中的E是可以出
现负数的,所以IEEE 754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001
然后,指数E从内存中取出还可以再分成三种情况:
E不全为0或不全为1
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将有效数字M前加上第一位的1,比如:0.5(1/2)的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为1.0*2^(-1),其阶码为-1+127=126,表示为01111110,而尾数1.0去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进制表示形式为:0 01111110 00000000000000000000000
E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值,有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数,这样做是为了表示±0,以及接近于0的很小的数字
E全为1
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s)
解释一下前面的题目哈:
下面,让我们回到一开始的问题:为什么 0x00000009 还原成浮点数,就成了 0.000000 ?
首先,9在计算机中是以补码存储的 9 -> 0000 0000 0000 0000 0000 0000 0000 1001,如果以浮点数读取的话,得到第一位符号位s=0,后面8位的指数 E=00000000 ,最后23位的有效数字M=000 0000 0000 0000 0000 1001,由于指数E全为0,所以符合上一节的第二种情况。因此,浮点数V就写成:

显然,V是一个很小的接近于0的正数,所以用十进制小数表示就是0.000000
再看例题的第二部分
请问浮点数9.0,如何用二进制表示?还原成十进制又是多少?
首先,浮点数9.0等于二进制的1001.0,即1.001×2^3

那么,第一位的符号位s=0,有效数字M等于001后面再加20个0,凑满23位,指数E等于3+127=130,即10000010,所以,写成二进制形式,应该是s+E+M,即

这个32位的二进制数,还原成十进制,正是 1091567616
相关文章:

数据在内存中的存储(deeper)
数据在内存中的存储(deeper) 一.数据类型的详细介绍二.整形在内存中的存储三.浮点型在内存中的存储 一.数据类型的详细介绍 类型的意义: 使用这个类型开辟内存空间的大小(大小决定了使用范围)如何看待内存空间的视角…...

算法修炼Day52|● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组
LeetCode:300.最长递增子序列 300. 最长递增子序列 - 力扣(LeetCode) 1.思路 dp[i]的状态表示以nums[i]为结尾的最长递增子序列的个数。 dp[i]有很多个,选择其中最大的dp[i]Math.max(dp[j]1,dp[i]) 2.代码实现 1class Solution {2 pub…...

使用 HTML、CSS 和 JavaScript 创建实时 Web 编辑器
使用 HTML、CSS 和 JavaScript 创建实时 Web 编辑器 在本文中,我们将创建一个实时网页编辑器。这是一个 Web 应用程序,允许我们在网页上编写 HTML、CSS 和 JavaScript 代码并实时查看结果。这是学习 Web 开发和测试代码片段的绝佳工具。我们将使用ifram…...

百望云联合华为发布票财税链一体化数智解决方案 赋能企业数字化升级
随着数据跃升为数字经济关键生产要素,数据安全成为整个数字化建设的重中之重。为更好地帮助企业发展,中央及全国和地方政府相继出台了多部与数据相关的政策法规,鼓励各领域服务商提供具有自主创新的软件产品与服务,帮助企业在合规…...

实现两个栈模拟队列
实现两个栈模拟队列 思路:可以想象一下左手和右手,两个栈:stack1(数据所在的栈) ,stack2(临时存放)。 入队:需要将入队 num 加在 stack1 的栈顶即可; 出队&am…...

无涯教程-TensorFlow - 单词嵌入
Word embedding是从离散对象(如单词)映射到向量和实数的概念,可将离散的输入对象有效地转换为有用的向量。 Word embedding的输入如下所示: blue: (0.01359, 0.00075997, 0.24608, ..., -0.2524, 1.0048, 0.06259) blues: (0.01396, 0.11887, -0.48963, ..., 0.03…...
Facebook AI mBART:巴别塔的硅解
2018年,谷歌发布了BERT(来自transformers的双向编码器表示),这是一种预训练的语言模型,在一系列自然语言处理(NLP)任务中对SOTA结果进行评分,并彻底改变了研究领域。类似的基于变压器…...

BDA初级分析——SQL清洗和整理数据
一、数据处理 数据处理之类型转换 字符格式与数值格式存储的数据,同样是进行大小排序, 会有什么区别? 以rev为例,看看字符格式与数值格式存储时,排序会有什么区别? 用cast as转换为字符后进行排序 SEL…...

汽车后视镜反射率测定仪
后视镜是驾驶员坐在驾驶室座位上直接获取汽车后方、侧方和下方等外部信息的工具。它起着“第三只眼睛”的作用。后视镜按安装位置划分通常分为车外后视镜、监视镜和内后视镜。外后视镜观察汽车后侧方监视镜观察汽车前下方内后视镜观察汽车后方及车内情况。用途不一样镜面结构也…...

Redis学习笔记
redis相关内容 默认端口6379 默认16个数据库,初始默认使用0号库 使用select 切换数据库 统一密码管理,所有库密码相同 dbsize:查看当前库key的数量 flushdb:清空当前库 flushall:清空全部库 redis是单线程 多路…...

韩顺平Linux 四十四--
四十四、rwx权限 权限的基本介绍 输入指令 ls -l 显示的内容如下 -rwxrw-r-- 1 root 1213 Feb 2 09:39 abc0-9位说明 第0位确定文件类型(d , - , l , c , b) l 是链接,相当于 windows 的快捷方式- 代表是文件是普通文件d 是目录,相…...

【支付宝小程序】分包优化教程
🦖我是Sam9029,一个前端 Sam9029的CSDN博客主页:Sam9029的博客_CSDN博客-JS学习,CSS学习,Vue-2领域博主 🐱🐉🐱🐉恭喜你,若此文你认为写的不错,不要吝啬你的赞扬,求收…...
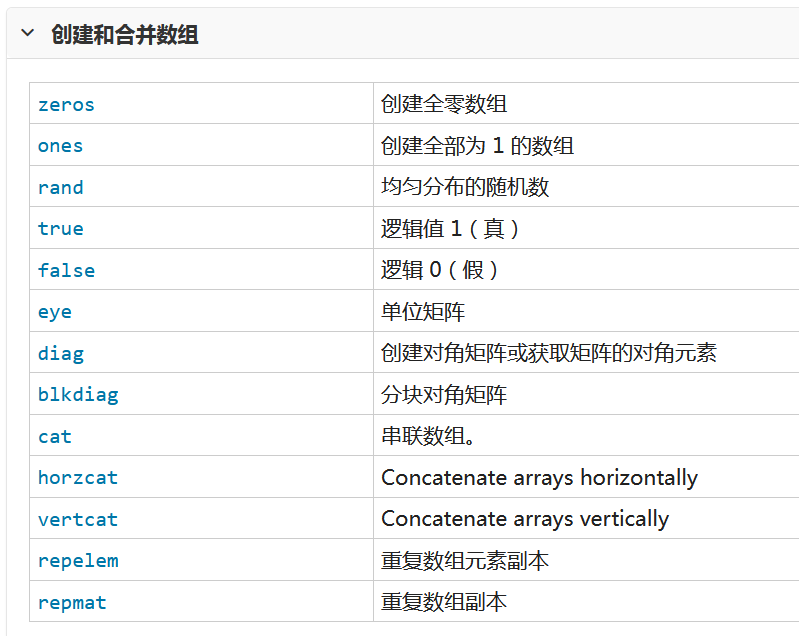
语言基础2 矩阵和数组
语言基础2 矩阵和数组 矩阵和数组是matlab中信息和数据的基本表示形式 可以创建常用的数组和网格 合并现有的数组 操作数组的形状和内容 以及使用索引访问数组元素 用到的函数列表如下 一 创建 串联和扩展矩阵 矩阵时按行和列排列的数据元素的二维数据元素的二维矩…...

springMVC中过滤器抛出异常,自定义异常捕获
在过滤器中引入org.springframework.web.servlet.HandlerExceptionResolver AutowiredQualifier("handlerExceptionResolver")private HandlerExceptionResolver resolver; // doFilter中处理if (条件1) {if (条件2) {resolver.resolveException(request, response, …...

图像检索技术研究:深度度量与深度散列在相似性学习中的应用比较与实践 - 使用Python与Jupyter环境
引言 在计算机视觉领域,图像检索是一个长期存在并持续受到研究者关注的重要话题。随着大数据时代的到来,如何高效、准确地从海量数据中检索到相似的图像成为一个巨大的挑战。传统的检索方法在大数据环境下表现不佳,而深度学习技术的崛起为图…...

CSS加载失败的6个原因
有很多刚刚接触 CSS 的新手有时会遇到 CSS 加载失败这个问题,但测试时,网页上没有显示该样式的问题,这就说明 CSS 加载失败了。出现这种状况一般是因为的 CSS 路径书写错,或者是在浏览器中禁止掉了 CSS 的加载,可以重新…...
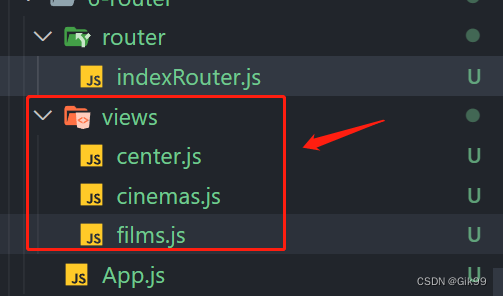
react之路由的安装与使用
一、路由安装 路由官网2021.11月初,react-router 更新到 v6 版本。使用最广泛的 v5 版本的使用 npm i react-router-dom5.3.0二、路由使用 2.1 路由的简单使用 第一步 在根目录下 创建 views 文件夹 ,用于放置路由页面 films.js示例代码 export default functio…...

基于RoCE的应用程序的MTU注意事项
目录 基于RoCE的应用程序的MTU注意事项 探测网络中的MTU设置 概要 原文 MTU测试结果 DOC: CentOS安装tshark抓包工具 基于RoCE的应用程序的MTU注意事项 原文:https://support.mellanox.com/s/article/MLNX2-117-1682kn InfiniBand协议最大传输单元ÿ…...

springboot集成Graphql相关问题汇总
1、idea在debug运行时出现java.lang.NoClassDefFoundError:kotlin/collections/AbstractMutableMap 解决:禁用idea dubugger中kotlin coroutine agent 见:https://stackoverflow.com/questions/70796177/after-the-spring-boot-source-code-is-compile…...

Angular16的路由守卫基础使用
Angular16的路由守卫基础使用 使用ng generate guard /guard/login命令生成guard文件因新版Angular取消了CanActivate的使用,改用CanActivateFn,因此使用router跳转需要通过inject的方式导入。 import { inject } from angular/core; import { CanActi…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
