区间预测 | MATLAB实现QRGRU门控循环单元分位数回归时间序列区间预测
区间预测 | MATLAB实现QRGRU门控循环单元分位数回归时间序列区间预测
目录
- 区间预测 | MATLAB实现QRGRU门控循环单元分位数回归时间序列区间预测
- 效果一览
- 基本介绍
- 模型描述
- 程序设计
- 参考资料
效果一览
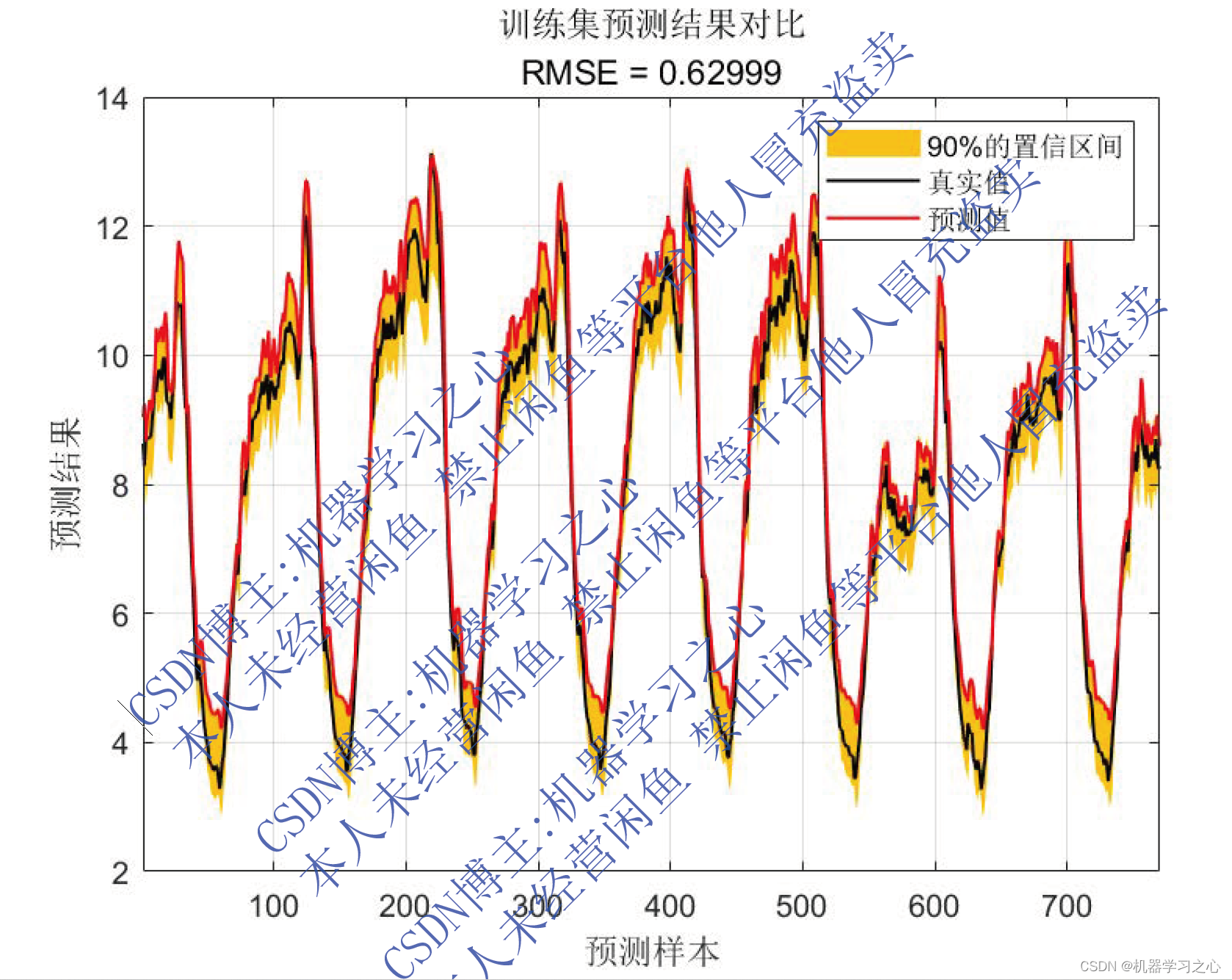
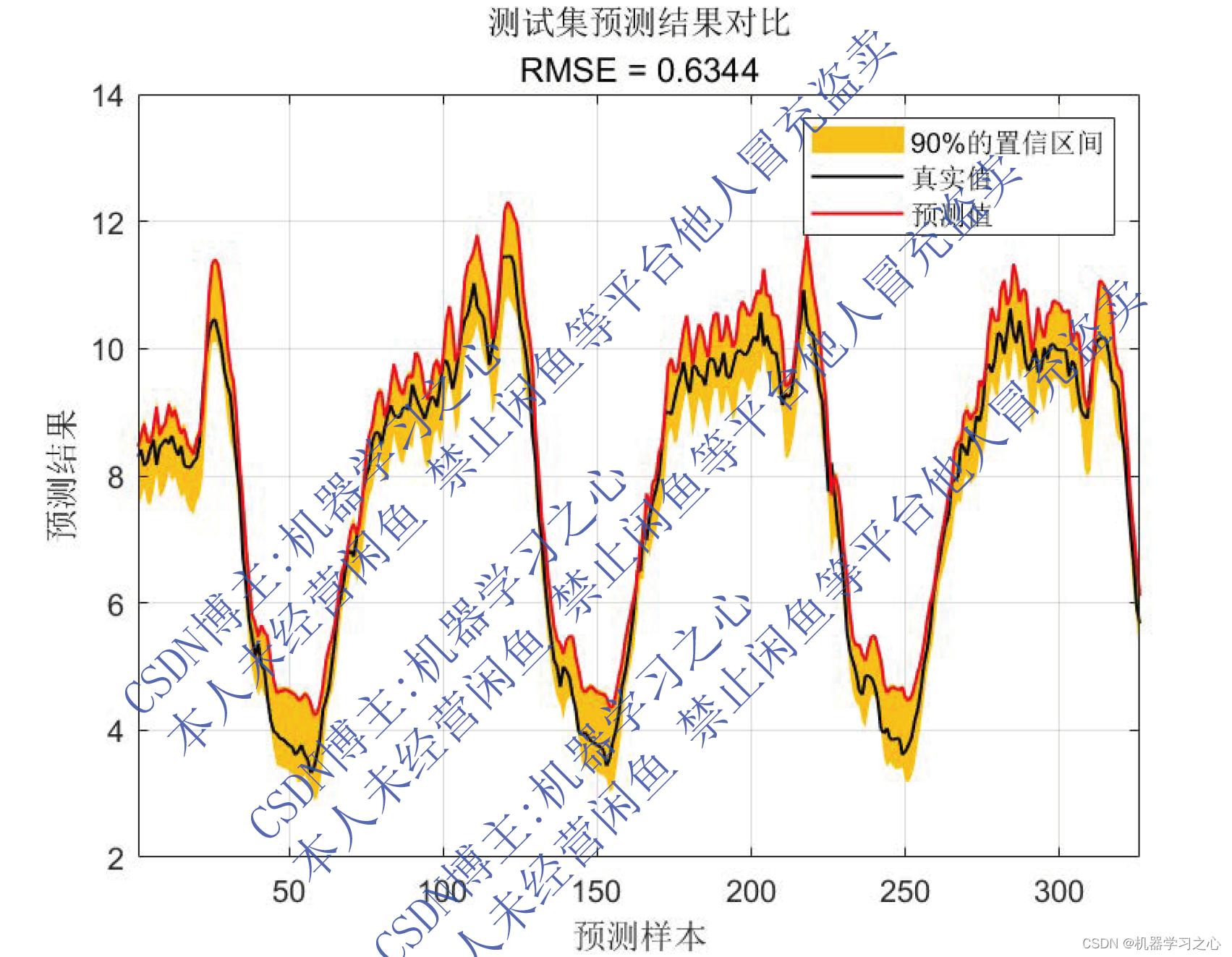
基本介绍
MATLAB实现QRGRU门控循环单元分位数回归时间序列区间预测。基于分位数回归的门控循环单元QRGRU的时间序列区间预测,多输入单输出模型 (Matlab完整程序和数据)
(主要应用于风速,负荷,功率)(Matlab完整程序和数据)
运行环境matlab2020及以上,输入多个特征,输出单个变量。
excel数据,方便学习和替换数据。
模型描述
分位数回归是简单的回归,就像普通的最小二乘法一样,但不是最小化平方误差的总和,而是最小化从所选分位数切点产生的绝对误差之和。如果 q=0.50(中位数),那么分位数回归会出现一个特殊情况 - 最小绝对误差(因为中位数是中心分位数)。我们可以通过调整超参数 q,选择一个适合平衡特定于需要解决问题的误报和漏报的阈值。GRU 有两个有两个门,即一个重置门(reset gate)和一个更新门(update gate)。从直观上来说,重置门决定了如何将新的输入信息与前面的记忆相结合,更新门定义了前面记忆保存到当前时间步的量。如果我们将重置门设置为 1,更新门设置为 0,那么我们将再次获得标准 RNN 模型。
程序设计
- 完整程序和数据获取方式(资源处下载):MATLAB实现QRGRU门控循环单元分位数回归时间序列区间预测
% gru
layers = [ ...sequenceInputLayer(inputSize,'name','input') %输入层设置gruLayer(numhidden_units1,'Outputmode','sequence','name','hidden1') dropoutLayer(0.3,'name','dropout_1')gruLayer(numhidden_units2,'Outputmode','last','name','hidden2') dropoutLayer(0.3,'name','drdiopout_2')fullyConnectedLayer(outputSize,'name','fullconnect') % 全连接层设置(影响输出维度)(cell层出来的输出层) %quanRegressionLayer('out',i)];
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
% 参数设定
opts = trainingOptions('adam', ...'MaxEpochs',10, ...'GradientThreshold',1,...'ExecutionEnvironment','cpu',...'InitialLearnRate',0.001, ...'LearnRateSchedule','piecewise', ...'LearnRateDropPeriod',2, ... %2个epoch后学习率更新'LearnRateDropFactor',0.5, ...'Shuffle','once',... % 时间序列长度'SequenceLength',1,...'MiniBatchSize',24,...'Verbose',0);
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%
% 网络训练
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
y = Test.demand;
x = Test{:,3:end};
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
% 归一化
[xnorm,xopt] = mapminmax(x',0,1);
xnorm = mat2cell(xnorm,size(xnorm,1),ones(1,size(xnorm,2)));
[ynorm,yopt] = mapminmax(y',0,1);
ynorm = ynorm';% 平滑层flattenLayer('Name','flatten')% GRU特征学习gruLayer(50,'Name','gru1','RecurrentWeightsInitializer','He','InputWeightsInitializer','He')% GRU输出gruLayer(NumOfUnits,'OutputMode',"last",'Name','bil4','RecurrentWeightsInitializer','He','InputWeightsInitializer','He')dropoutLayer(0.25,'Name','drop3')% 全连接层fullyConnectedLayer(numResponses,'Name','fc')regressionLayer('Name','output') ];layers = layerGraph(layers);layers = connectLayers(layers,'fold/miniBatchSize','unfold/miniBatchSize');
————————————————
版权声明:本文为CSDN博主「机器学习之心」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/kjm13182345320/article/details/130447132
参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/127931217
[2] https://blog.csdn.net/kjm13182345320/article/details/127418340
[3] https://blog.csdn.net/kjm13182345320/article/details/127380096
相关文章:

区间预测 | MATLAB实现QRGRU门控循环单元分位数回归时间序列区间预测
区间预测 | MATLAB实现QRGRU门控循环单元分位数回归时间序列区间预测 目录 区间预测 | MATLAB实现QRGRU门控循环单元分位数回归时间序列区间预测效果一览基本介绍模型描述程序设计参考资料 效果一览 基本介绍 MATLAB实现QRGRU门控循环单元分位数回归时间序列区间预测。基于分位…...
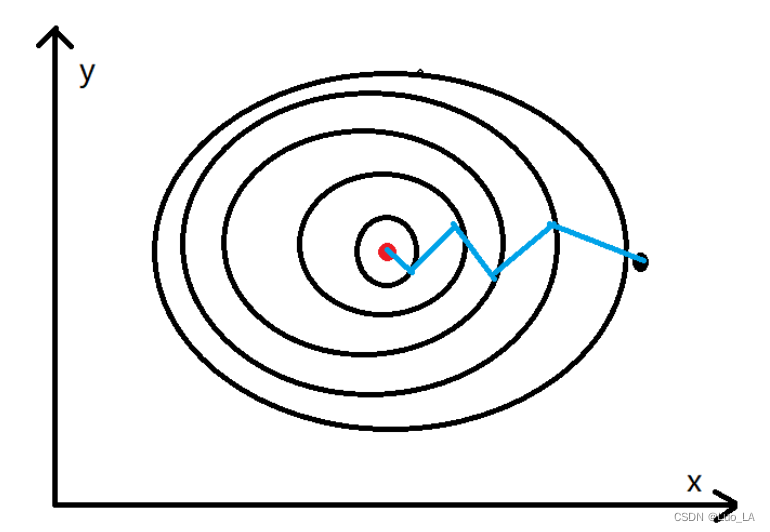
改善神经网络——优化算法(mini-batch、动量梯度下降法、Adam优化算法)
改善神经网络——优化算法 梯度下降Mini-batch 梯度下降(Mini-batch Gradient Descent)指数加权平均包含动量的梯度下降RMSprop算法Adam算法 优化算法可以使神经网络运行的更快,机器学习的应用是一个高度依赖经验的过程,伴随着大量…...
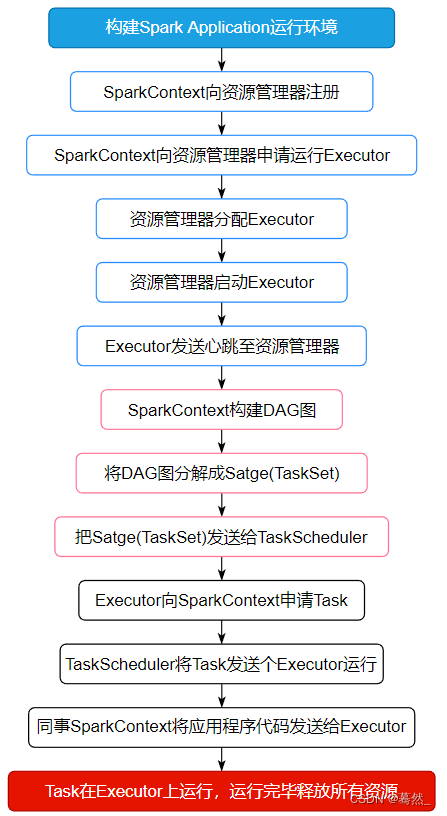
大数据面试题:Spark的任务执行流程
面试题来源: 《大数据面试题 V4.0》 大数据面试题V3.0,523道题,679页,46w字 可回答:1)Spark的工作流程?2)Spark的调度流程;3)Spark的任务调度原理…...

通过 Amazon SageMaker JumpStart 部署 Llama 2 快速构建专属 LLM 应用
来自 Meta 的 Llama 2 基础模型现已在 Amazon SageMaker JumpStart 中提供。我们可以通过使用 Amazon SageMaker JumpStart 快速部署 Llama 2 模型,并且结合开源 UI 工具 Gradio 打造专属 LLM 应用。 Llama 2 简介 Llama 2 是使用优化的 Transformer 架构的自回归语…...

ansible远程执行命令
一、ansible简介 需要在一台机器上搭建ansible环境,且配置目的ip的密码,通道没有问题即可下发命令 使用的通道是ssh(端口:36000) 二、搭建细节 1、安装ansible yum install -y ansible 2、把目的ip密码写到配置…...

Windows快速恢复丢失的颜色校准
场景 有时开机或启动某个软件后,颜色校准(设置项:校准显示器颜色)会丢失,每次重新设置很麻烦。 文章首发及后续更新:https://mwhls.top/4723.html,无图/无目录/格式错误/更多相关请至首发页查看…...

Vue安装单文件组件
安装 npm npm 全称为 Node Package Manager,是一个基于Node.js的包管理器,也是整个Node.js社区最流行、支持的第三方模块最多的包管理器。 npm -v由于网络原因 安装 cnpm npm install -g cnpm --registryhttps://registry.npm.taobao.org安装 vue-cli…...

小白的Node.js学习笔记大全---不定期更新
Node.js是什么 Node. js 是一个基于 Chrome v8 引擎的服务器端 JavaScript 运行环境Node. js 是一个事件驱动、非阻塞式I/O 的模型,轻量而又高效Node. js 的包管理器 npm 是全球最大的开源库生态系统 特性 单一线程 Node.js 沿用了 JavaScript 单一线程的执行特…...
)
第二周晨考自测(2.0)
1.冒泡排序 冒泡排序是数组解构中的常见排序算法之一。规则如下:先遍历数组,让相邻的两个数据进行比较,如果前一个比后一个大,那么就把这两个数据交换位置,经过一轮遍历之后,最大的那个数字就排在数组最后…...
(单视图测量))
计算机视觉之三维重建(三)(单视图测量)
2D变换 等距变换 旋转平移保留形状、面积通常描述刚性物体运动 相似变换 在等距变换的基础增加缩放特点 射影变换 共线性、四共线点的交比保持不变 仿射变换 面积比值、平行关系等不变仿射变换是特殊的射影变换 影消点与影消线 2D无穷远点 两直线的交点可由两直线的…...

docker 批量快速删除容器和镜像
一、批量删除镜像 如果你想要批量删除 Docker 镜像,可以使用各种命令。以下是一些示例: 1. 删除所有镜像: docker rmi $(docker images -q) 2. 删除所有未标记的镜像(即 <none> 镜像): docker rmi $(docker images -f "dangling=true" -q) 请注意…...
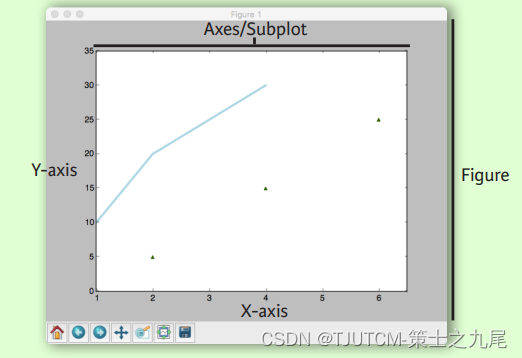
【数据分析入门】Matplotlib
目录 零、图形解析与工作流0.1 图形解析0.2 工作流 一、准备数据1.1 一维数据1.2 二维数据或图片 二、绘制图形2.1 画布2.2 坐标轴 三、绘图例程3.1 一维数据3.2 向量场3.3 数据分布3.4 二维数据或图片 四、自定义图形4.1 颜色、色条与色彩表4.2 标记4.3 线型4.4 文本与标注4.5…...
mongodb.使用自带命令工具导出导入数据
在一次数据更新中,同事把老数据进行了清空操作,但是新的逻辑数据由于某种原因(好像是她的电脑中病毒了),一直无法正常连接数据库进行数据插入,然后下午2点左右要给甲方演示,所以要紧急恢复本地的…...

IndexError: tensors used as indices must be long, byte or bool tensors
运行出现报错。修改数据格式 输出sample_ids的值,可以看到数据类型是 torch.int32 解决 需要将sample_ids类型转为long,修改方式: idx idx.type(torch.long)或 idx self.tensor(idx, dtypetorch.long)参考: IndexError: tenso…...

设计模式 : 单例模式笔记
文章目录 一.单例模式二.单例模式的两种实现方式饿汉模式懒汉模式 一.单例模式 一个类只能创建一个对象,这样的类的设计模式就称为单例模式,该模式保证系统中该类只能有一个实例(并且父子进程共享),一个很典型的单例类就是CSTL的内存池C单例模式的基本设计思路: 私有化构造函数…...

深度优先搜索算法
目录 4.1 二叉树的最大深度(简单):深度优先搜索 4.2 对称二叉树(简单):递归 4.3 岛屿数量(中等):深度优先搜索 4.4 岛屿的最大面积(中等)&…...

k8s ----POD控制器详解
目录 一:pod控制器 1、Pod控制器及其功用 2、pod控制器类型 3、Pod与控制器之间的关系 二:Deployment 三:SatefulSet 1、StatefulSet组成 2、为什么要有headless? 3、为什么要有volumeClaimTemplate? 4、实现…...
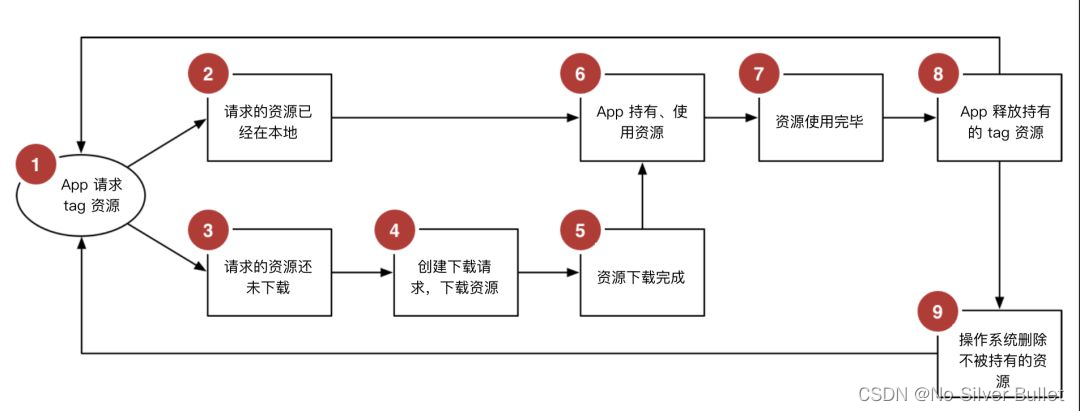
ReactNative进阶(三十四):ipa Archive 阶段报错error: Multiple commands produce问题修复及思考
文章目录 一、前言二、问题描述三、问题解决四、拓展阅读五、拓展阅读 一、前言 在应用RN开发跨平台APP阶段,从git中拉取项目,应用Jenkins进行组包时,发现最终生成的ipa安装包版本号始终与项目中设置的版本号不一致。 二、问题描述 经过仔…...

MySQL索引ES索引
MySQL MySQL索引的种类 按照索引列值的唯一性:索引可分为唯一索引和非唯一索引; 唯一索引:此索引的每一个索引值只对应唯一的数据记录,对于单列唯一性索引,这保证单列不包含重复的值。对于多列唯一性索引,保证多个值的组合不重复。主键索引是唯一索引的特定类型。该索引…...
webSocket 聊天室 node.js 版
全局安装vue脚手架 npm install vue/cli -g 创建 vue3 ts 脚手架 vue create vue3-chatroom 后端代码 src 同级目录下建 server: const express require(express); const app express(); const http require(http); const server http.createServer(app);const io req…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
