插入排序优化——超越归并排序的超级算法
插入排序及优化
- 插入排序算法
- 算法讲解
- 数据模拟
- 代码
- 优化思路
- 一、二分查找
- 二、copy函数
- 优化后代码
- 算法的用途
- 题目:数星星(POJ2352 star)
- 输入输出格式
- 输入格式:
- 输出格式
- 输入输出样例
- 输入样例
- 输出样例
- 题目讲解
- 步骤如下
- AC 代码
插入排序算法
在了解如何改进插入排序之前,我们先要了解插入排序的基本算法:
算法讲解
插入排序对于少量元素的排序,是一个有效的算法 。
插入排序是一种简单的排序方法,它是将一个数据插入到已经排好序的有序数组,从而形成一个新的有序数组。
插入排序的工作方式像许多人排序扑克牌:
我们每次从桌子上拿走一张牌并将其插入到手中正确的位置。
为了找到它的正确位置,我们从右到左将它与手中的每张牌进行比较。
因此,手上的牌总是有序。
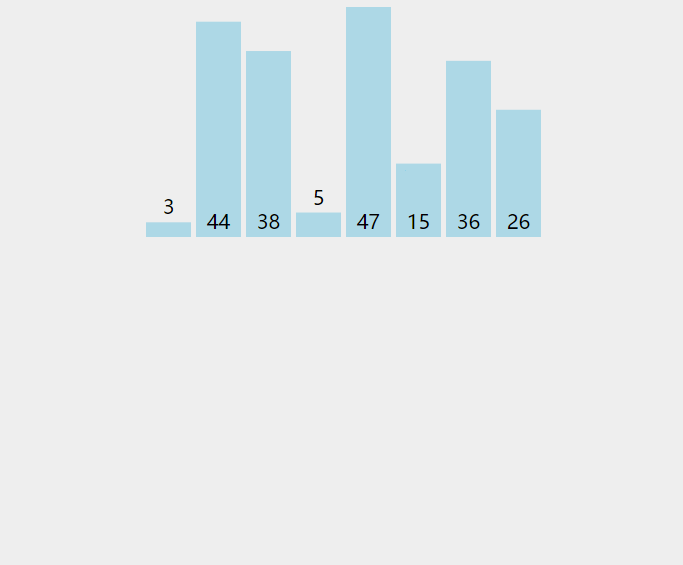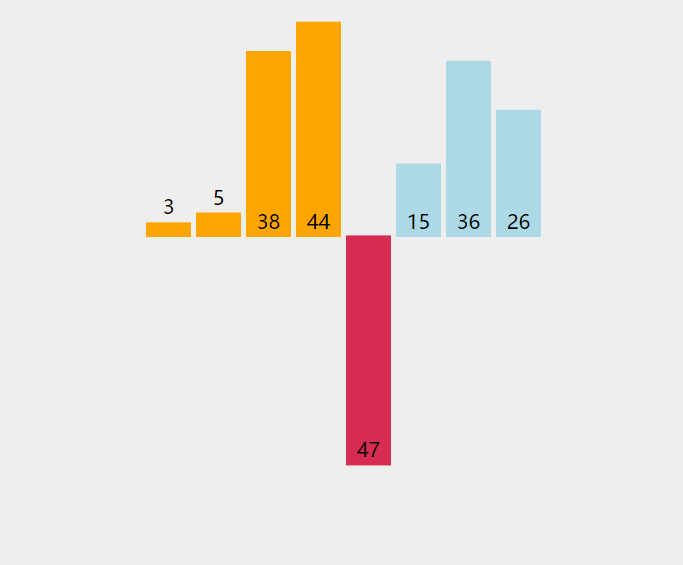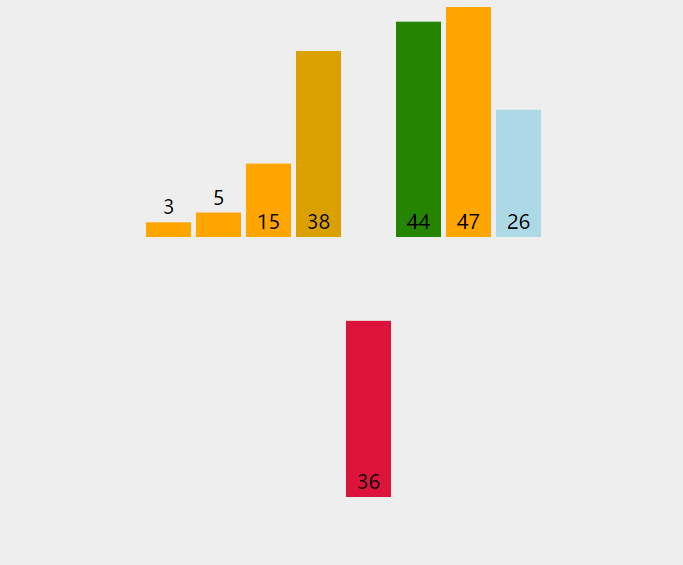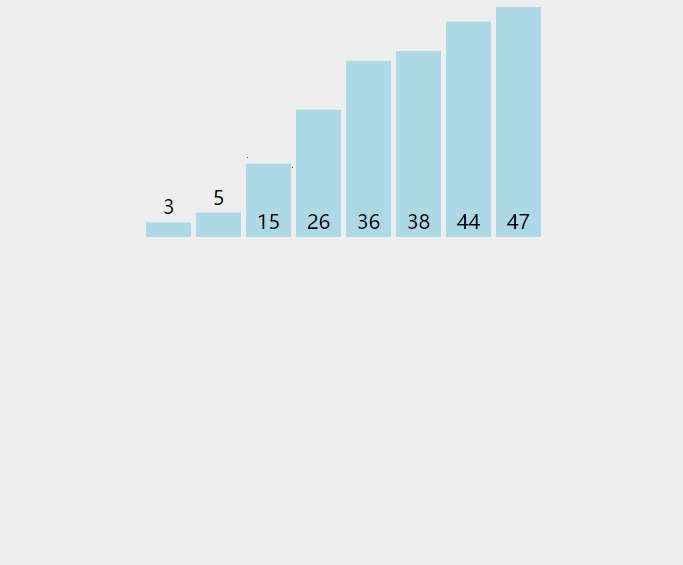
数据模拟
原本要排序的数为 5 3 4 2 9 1,从小到大排序。
3 5 4 2 9 1 // 将3放到合适的位置(5前面)3 4 5 2 9 1 // 将4放到合适的位置(3、5中间)2 3 4 5 9 1 // 将2放到合适的位置(最前面)2 3 4 5 9 1 // 将9放到合适的位置(最后面)1 2 3 4 5 9 // 将1放到合适的位置(最前面)
排序结束!!!
代码
#include <iostream>
using namespace std;
int n,a[2000]; //定义数据个数n,排序数组a
int main()
{cin >>n; //输入个数for (int i=1;i<=n;i++)cin >>a[i]; //输入数据for (int i=2;i<=n;i++) //第一个数本身只有一个元素,所有有序,因此不用参与排序{int j,k=a[i]; //记录下当前元素for (j=i-1;j>0;j--){if (a[j]>k) //若前面一个数大于当前元素a[j+1]=a[j]; //则将前面一个元素往后移动elsebreak; //否则:说明当前元素已经找到了合适的位置,推出循环}a[j+1]=k; //将当前元素放入数组的合适的位置/* 输出排序的过程for (int j=1;j<=n;j++)cout <<a[j] <<" ";cout <<endl;*/}for (int i=1;i<=n;i++)cout <<a[i] <<" "; //输出排序好的数组return 0;
}
优化思路
我们发现,插入排序的过程浪费在了查找合适的位置上,那么怎么优化呢?
我们知道,插入排序一直在维护 前 i i i个数是有序的,那么如何快速在有序的数列中查找一个小于(或大于)自己的数呢?
一、二分查找
二分!!!!
那么这样我们就讲查找的时间从 O ( n ) O(n) O(n)缩短为 O ( n l o g ( n ) ) O(n~log(n)) O(n log(n))!!
忍不住激动!!
可是找到位置不够,还要进行移动啊。移动的时间复杂度是 O ( n ) O(n) O(n)那么这样非但没有优化,反而还增加了查找的时间。。。
希望瞬间破灭!!
但是我会向它屈服吗???
会 吗?
明显不会!
二、copy函数
我们可以使用一个 S T L STL STL库里面的一个函数:
copy(a,a+n,a+1);
c o p y copy copy函数!!
这个函数可以在 O ( 1 ) O(1) O(1)的时间范围内将数组的某一段移动到,
使用方法:
以上面的操作为例子,这表明:
- 以 a a a数组的第 0 0 0位为开头
- 以 a a a数组的第 n − 1 n-1 n−1位位结尾
- 将它移动到开头位第 1 1 1位的位置
那么,这就好办了,只需要要讲两个结合起来,一个速度与归并排序相当,代码比归并排序简短许多的超级优化插入排序代码诞生了:
优化后代码
#include <bits/stdc++.h>
#define N 2000000
using namespace std;
int n,x,y,f,t[N],k[N];
int main() {scanf("%d",&n);for (int i=1; i<=n; i++) {scanf("%d",&x);f=upper_bound(t+1,t+i,x)-t; //记录二分的位置copy(t+f,t+i,t+f+1); //copyt[f]=x; //存入数组}for (int i=1; i<=n; i++) {printf("%d ",t[i]);}return 0;
}
输入数据:
5
4 9 1021 54 3
输出数据:
3 4 9 54 1021
也是对了好吧~~
算法的用途
这个算法可以快速的在有序数列里面进行操作,也是异常的方便快捷,代码超级简短!!
下面给一道可以用这个算法解决的问题:
题目:数星星(POJ2352 star)
天文学家经常观察星象图。星象图中用平面上的点来表示一颗星星,每一颗星星都有一个笛卡尔坐标。设定星星的等级为其左下角星星的总数。天文学家们想知道星星等级的分布情况。

比如上图, 5 5 5号星星的等级为 3 3 3(其左下角有编号为 1 1 1、 2 2 2、 4 4 4星星共三颗)。 2 2 2号星星和 4 4 4号星星的等级为 1 1 1。在上图中只有一颗星星等级为 0 0 0,两颗星星等级为 1 1 1,一颗星星等级为 2 2 2,一颗星星等级为 3 3 3。
给定一个星象图,请你写一个程序计算各个等级的星星数目。
输入输出格式
输入格式:
输入的第一行包含星星的总数 N ( 1 < = N < = 15000 ) N (1<=N<=15000) N(1<=N<=15000)。接下来 N N N行,描述星星的坐标 ( X , Y ) (X,Y) (X,Y)( X X X和 Y Y Y用空格分开, 0 ≤ X , Y ≤ 32000 0\le X,Y\le 32000 0≤X,Y≤32000)。星象图中的每个点处最多只有一颗星星。所有星星按 Y Y Y坐标升序排列。 Y Y Y坐标相等的星星按 X X X坐标升序排列。
输出格式
输出包含 N N N行,每行一个整数。第一行包含等级 0 0 0的星星数目,第二行包含等级 1 1 1的星星数目,依此类推,最后一行包含等级为 N − 1 N-1 N−1的星星数目。
输入输出样例
输入样例
5
1 1
5 1
7 1
3 3
5 5
输出样例
1
2
1
1
0
题目讲解
由于输入数据有序,所以在第 i i i颗星星左下角的星星一定在 i i i前面!!原理自己想想就知道了~~
所以其实就是求在点 i i i前面的点中,有多少个的 X X X坐标是比 i i i的 X X X坐标要小的,因此直接考虑插入排序做法:
步骤如下
- 输入星星的数量 n n n
- 循环从 1 1 1到 n n n
- 每次输入当前点的 X X X和 Y Y Y
- 用二分查找当前点的 X X X应当放在哪个位置
- 用变了量 f f f记录位置, f − 1 f-1 f−1就是当前星星的等级
- 用 c o p y copy copy将数据,从当前合适的位置开始,到 i − 1 i-1 i−1往后移动一位
- 将当前数据存入排序数组
- 用另一个数组标记这个等级的星星 + + ++ ++
- 循环输出每个级别的星星
AC 代码
#include <bits/stdc++.h>
#define N 20000
using namespace std;
int n,x,y,f,t[N],k[N];
int main() {scanf("%d",&n);for (int i=1; i<=n; i++) {scanf("%d%d",&x,&y);f=upper_bound(t+1,t+i,x)-t;copy(t+f,t+i,t+f+1);t[f]=x;k[f-1]++;}for (int i=0; i<n; i++) {printf("%d\n",k[i]);}return 0;
}
相关文章:

插入排序优化——超越归并排序的超级算法
插入排序及优化 插入排序算法算法讲解数据模拟代码 优化思路一、二分查找二、copy函数 优化后代码算法的用途题目:数星星(POJ2352 star)输入输出格式输入格式:输出格式 输入输出样例输入样例输出样例 题目讲解步骤如下AC 代码 插入…...

面试之快速学习STL-容器适配器
1. 容器适配器 简单的理解容器适配器,其就是将不适用的序列式容器(包括 vector、deque 和 list)变得适用。 注意:默认使用的基础容器不代表一定只能用它,比如queue可以用deque,list。 如果你希望你的qu…...

性能比较 - Spring Boot 应用程序中的线程池与虚拟线程 (Project Loom)
本文比较了 Spring Boot 应用程序中的不同请求处理方法:ThreadPool、WebFlux、协程和虚拟线程 (Project Loom)。 在本文中,我们将简要描述并粗略比较可在 Spring Boot 应用程序中使用的各种请求处理方法的性能。 高效的请求处理在开发高性能后端…...

rust学习-打印结构体中的vec
write! 宏 将格式化后的数据写入到一个缓冲区(buffer),而不是直接打印到标准输出或文件中。 这个缓冲区可以是字符串,也可以是需要写入的文件的缓冲区。 write!(writer, format_string, expr1, expr2, ...);writer 参数是一个实…...
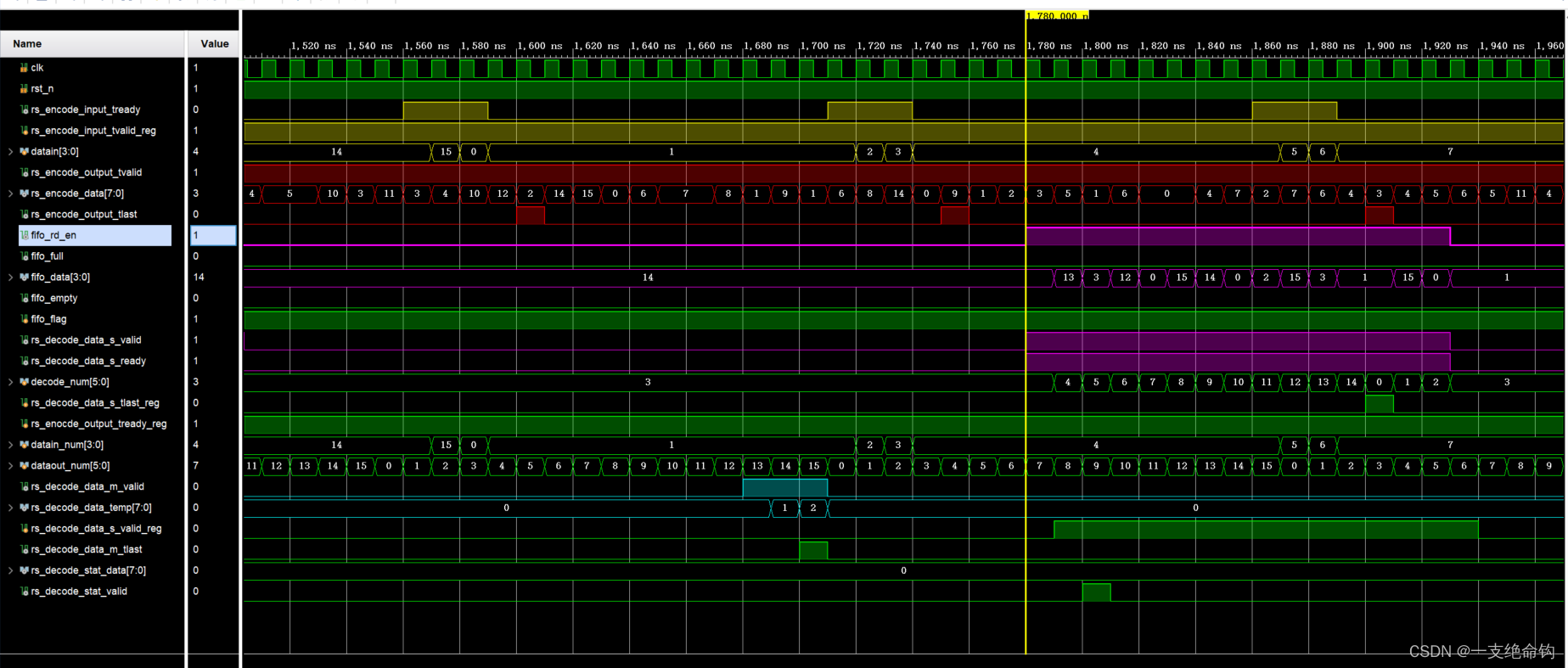
FPGA: RS译码仿真过程
FPGA: RS译码仿真过程 在上一篇中记录了在FPGA中利用RS编码IP核完成信道编码的仿真过程,这篇记录利用译码IP核进行RS解码的仿真过程,带有程序和结果。 1. 开始准备 在进行解码的过程时,同时利用上一篇中的MATLAB仿真程序和编码过程&#x…...

PostgreSQL 查询数据表、视图信息
--获得指定schema范围内的所有表和视图的列表,可指定一个排除表前缀模式with param as (select public,iit as schema_name,db2g% as exclude_pattern),base_info as (--获得所有基表select pg_namespace.nspname as schema_name, a.relname as tbl_name ,TBL as tb…...
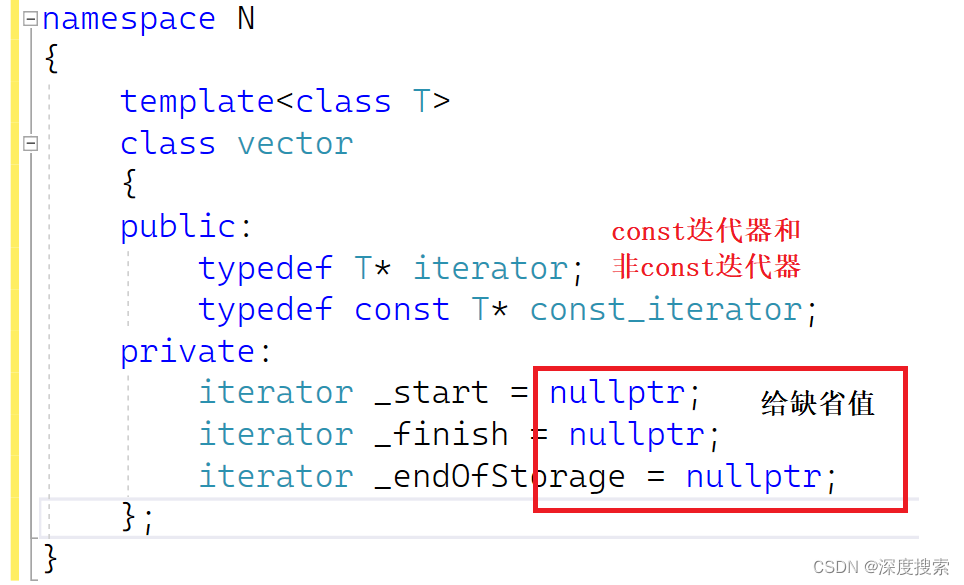
手撕vector容器
一、vector容器的介绍 vector是表示可变大小数组的序列容器。就像数组一样,vector也采用的连续存储空间来存储元素,但是又不像数组,它的大小是可以动态改变的,而且它的大小会被容器自动处理。 总结:vector是一个动态…...
PyMuPDF`库实现PDF旋转功能
本文介绍了一个简单的Python应用程序,用于将PDF文件转换为旋转90度的PDF文件。主要用于csdn网站中导出的博客pdf是横向的,看起来不是很方便,才想到用python编制一个将pdf从横向转为纵向的功能。 功能 该PDF转换工具具有以下功能:…...
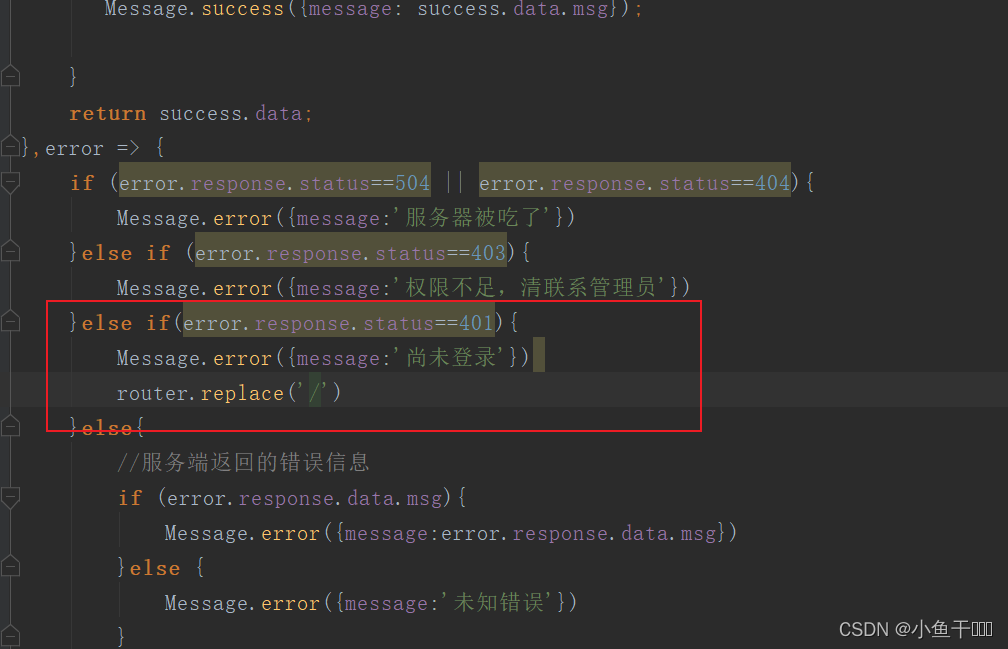
微人事 登录问题完善
重启服务端的时候,发现前端页面会操作不了,这样后端session会失效,我们就需要让页面重新跳转到登录页 springsecurity配置类后端配置 前端拦截器进行拦截跳转...

【业务功能篇64】安装docker容器,在docker上安装mysql
docker教程: https://www.runoob.com/docker/docker-tutorial.html卸载docker 较旧的 Docker 版本称为 docker 或 docker-engine 。如果已安装这些程序,请卸载它们以及相关的依赖项。 yum remove docker docker-client docker-client-latest docker-co…...

MyBatis的基本概念和核心组件
MyBatis的基本概念 MyBatis 是一款优秀的持久层框架,它支持定制化 SQL、存储过程以及高级映射。MyBatis 避免了几乎所有的 JDBC 代码和手动设置参数以及获取结果集。MyBatis 可以使用简单的 XML 或注解来配置和映射原生信息,将接口和 Java 的 POJOs(Pla…...

sql update执行返回0,能否判断数据不存在
答案:不能。 update执行返回0的情况 1、没有找到需要更新的数据,就是这条记录不存在 例如:where后面的条件是id0,那这条记录肯定是不存在的,返回结果是0 2、更新时的数据和要更新的数据完全一致时 例如:更…...
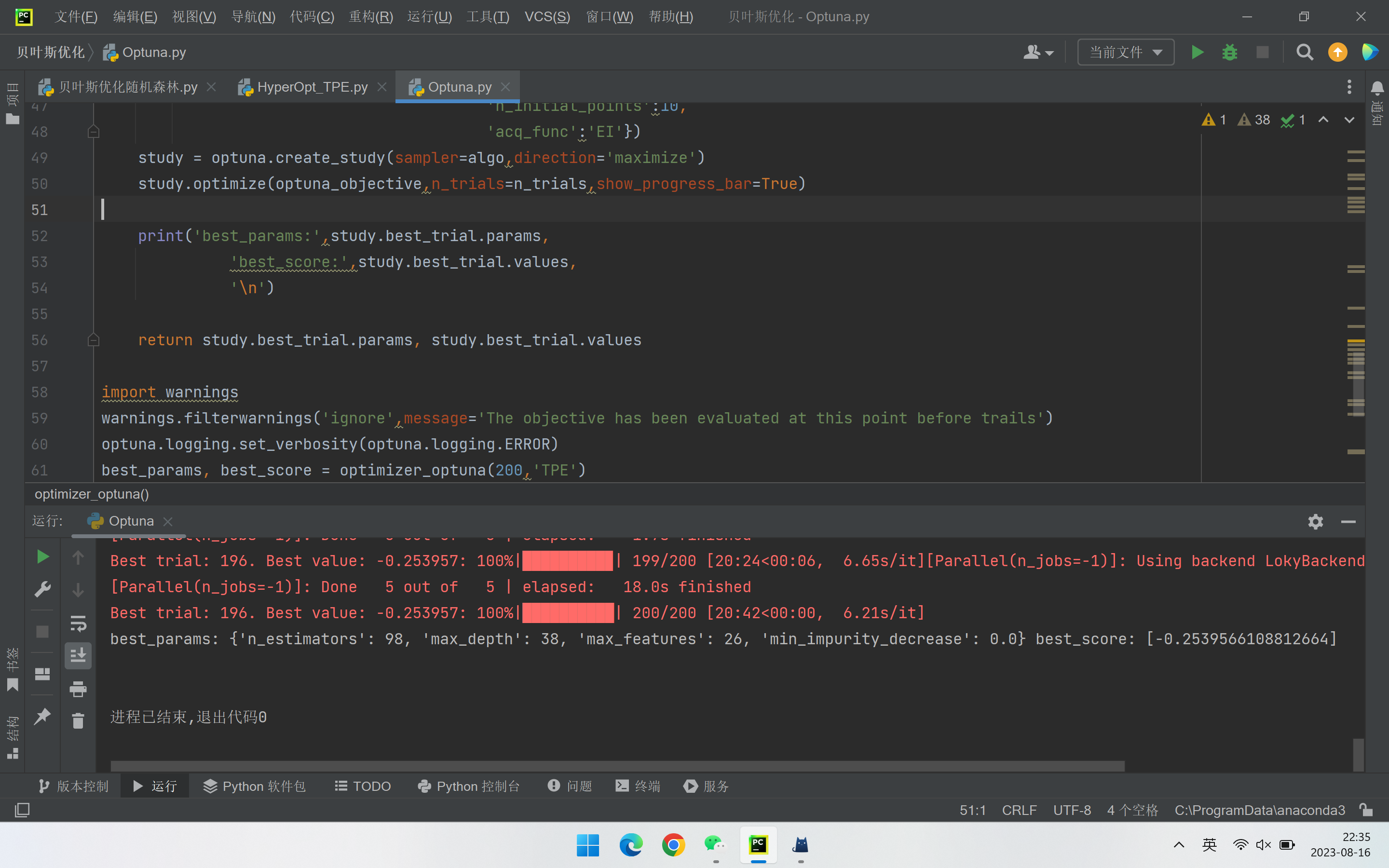
数据分析 | 调用Optuna库实现基于TPE的贝叶斯优化 | 以随机森林回归为例
1. Optuna库的优势 对比bayes_opt和hyperoptOptuna不仅可以衔接到PyTorch等深度学习框架上,还可以与sklearn-optimize结合使用,这也是我最喜欢的地方,Optuna因此特性可以被使用于各种各样的优化场景。 2. 导入必要的库及加载数据 用的是sklea…...
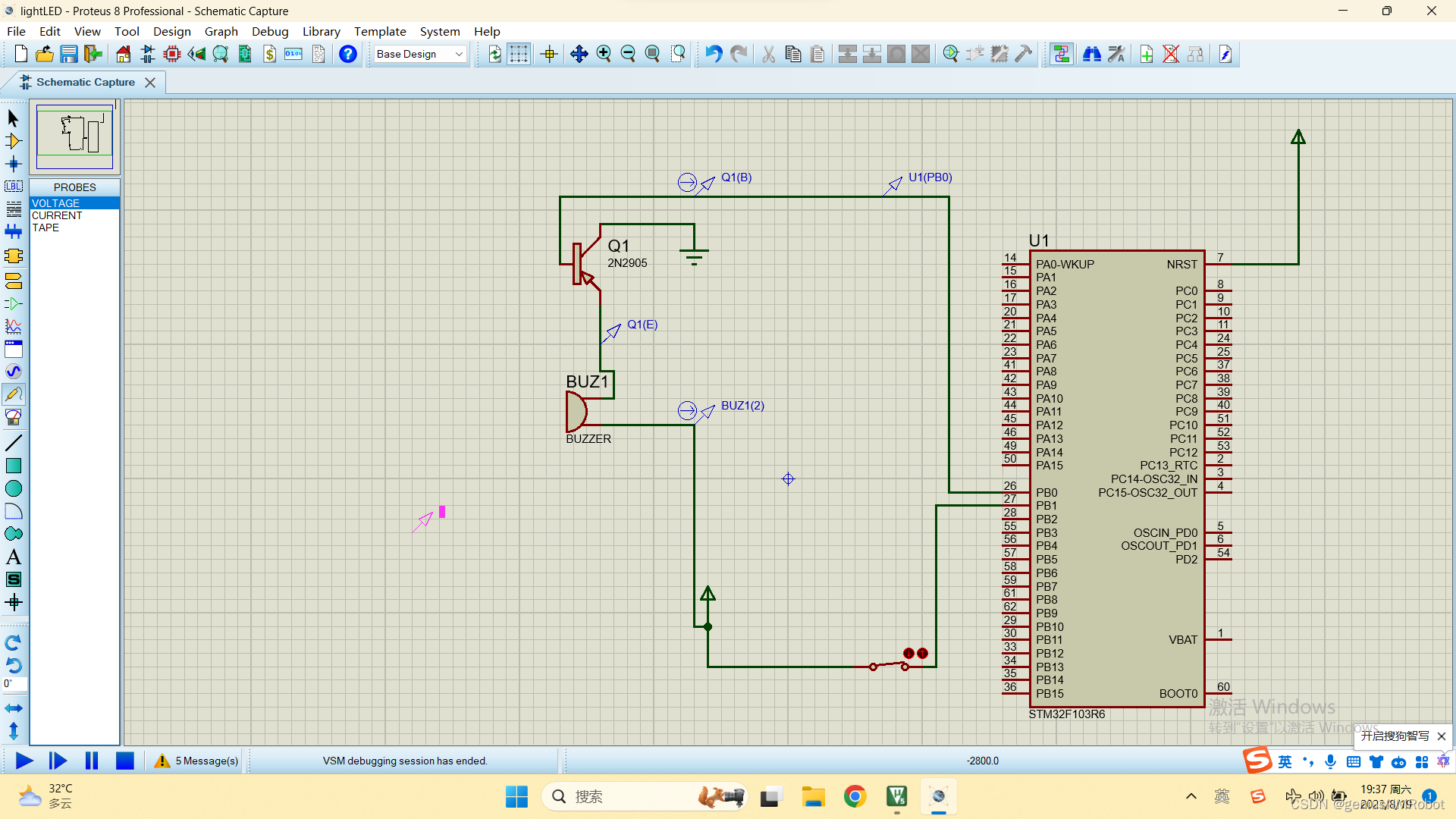
stm32单片机开关输入控制蜂鸣器参考代码(附PROTEUS电路图)
说明:这个buzzer的额定电压需要改为3V,否则不会叫,源代码几乎是完全一样的 //gpio.c文件 /* USER CODE BEGIN Header */ /********************************************************************************* file gpio.c* brief Thi…...

打印X型的图案
int main() {int n0;int i0;int j0;scanf("%d",&n);for(i0;i<n;i){for(j0;j<n;j){if(ij){printf("*");}else if((ij)n-1){printf("*");}elseprintf(" ");}printf("\n");}return 0; }...
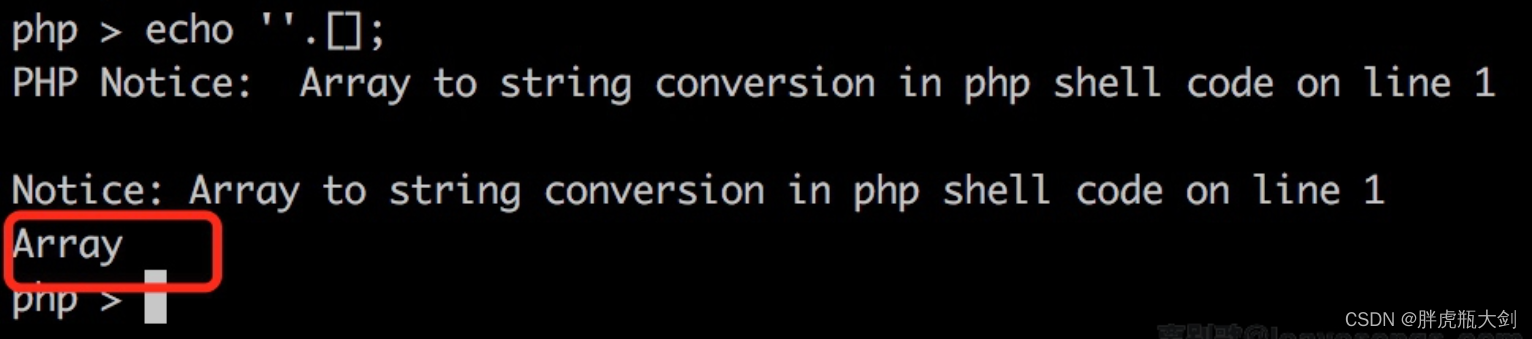
不含数字的webshell绕过
异或操作原理 1.首先我们得了解一下异或操作的原理 在php中,异或操作是两个二进制数相同时,异或(相同)为0,不同为1 举个例子 A的ASCII值是65,对应的二进制值是0100 0001 的ASCII值是96,对应的二进制值是 0110 000…...

Mac上传项目源代码到GitHub的修改更新
Mac上传项目源代码到GitHub的修改更新 最近在学习把代码上传到github,不得不说,真的还挺方便 这是一个关于怎样更新项目代码的教程。 首先,在本地终端命令行打开至项目文件下第一步:查看当前的git仓库状态,可以使用git…...

Android6:片段和导航
创建项目Secret Message strings.xml <resources><string name"app_name">Secret Message</string><string name"welcome_text">Welcome to the Secret Message app!Use this app to encrypt a secret message.Click on the Star…...
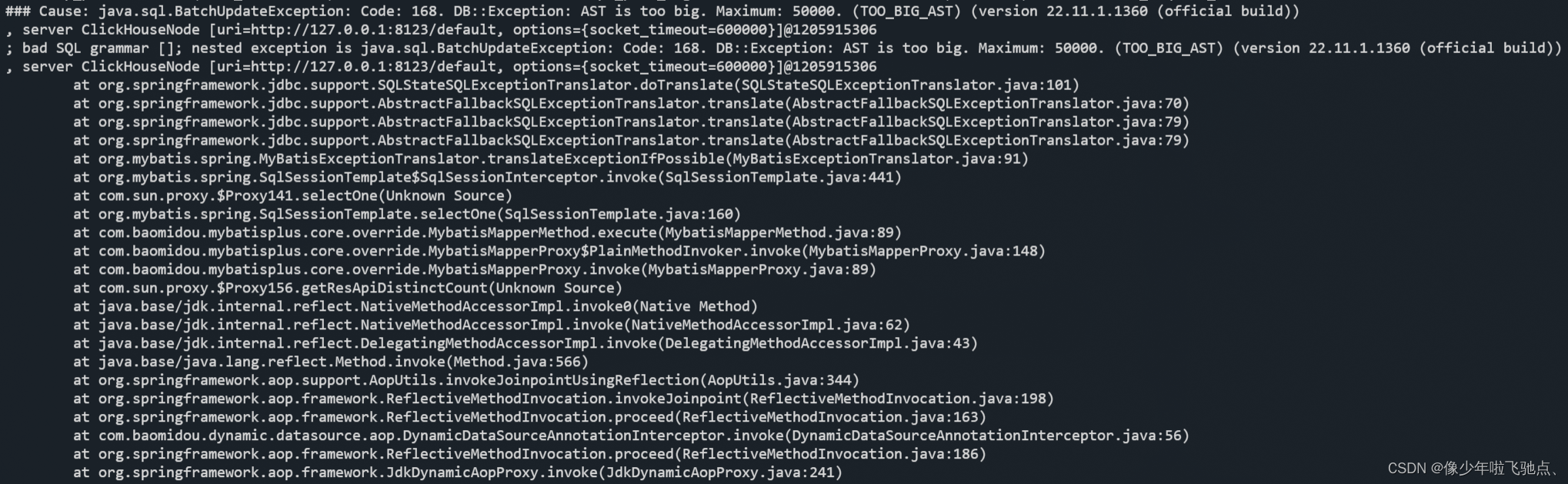
ClickHouse AST is too big 报错问题处理记录
ClickHouse AST is too big 报错问题处理记录 问题描述问题分析解决方案1、修改系统配置2、修改业务逻辑 问题描述 项目中统计报表的查询出现 AST is too big 问题,报错信息如下: 问题分析 报错信息显示 AST is too big。 AST 表示查询语法树中的最大…...

DPDK系列之二十七DIDO
一、DIDO介绍 随着计算机技术发展,特别是应用技术的快速发展。应用场景对计算机的处理速度几乎已经到了疯狂的地步。说句大白话,再快的CPU也嫌慢。没办法,CPU和IO等技术基本目前都处在了瓶颈之处,大幅度提高,短时间内…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
