Programming abstractions in C阅读笔记: p118-p122
《Programming Abstractions In C》学习第49天,p118-p122,总结如下:
一、技术总结
1.随机数
(1)seed
p119,“The initial value–the value that is used to get the entire process start–is call a seed for the random generator.”
二、数学总结
1.均匀分布(uniform distribution)
均匀分布属于概率论和统计学范畴,有连续性均匀分布和离散型均匀分布。
参考:(1)连续性均匀分布(continuous uniform distribution):(2)离散型均匀分布(discrte uniform distribution):
三、英语总结
1.discern是什么意思?
答:dis-(“off, away”) + cernere(“distinguish, seperate, shif”),“to see, recorgnize, understand sth that is not clear(识别)”,当使用这个单词的时候,表示“被识别”的对象并不是那么“clear”。
2.against什么意思?
p120,“Finally, every implementation needs to include its own interface so the compiler can check the prototypes against the actual definitions.”。这里之所以要把against抽出来说,是因为against很多地方会用到,但要说直接翻译成什么词,却不是那么好直接给出答案,这里做一个总结。against总体的意思是“prep. opposite/toward”。
3.suffice什么意思?
答:i. to be enough。形容词是“sufficent”。p120,“The comments in the interface should suffice.”(接口中定义的注释应该足够了)。
三、参考资料
1. 编程
(1)Eric S.Roberts,《Programming Abstractions in C》:https://book.douban.com/subject/2003414
2. 英语
(1)Etymology Dictionary:https://www.etymonline.com
(2) Cambridage Dictionary:https://dictionary.cambridge.org
欢迎搜索及关注:编程人(a_codists)
相关文章:

Programming abstractions in C阅读笔记: p118-p122
《Programming Abstractions In C》学习第49天,p118-p122,总结如下: 一、技术总结 1.随机数 (1)seed p119,“The initial value–the value that is used to get the entire process start–is call a seed for the random ge…...

2023国赛数学建模思路 - 案例:ID3-决策树分类算法
文章目录 0 赛题思路1 算法介绍2 FP树表示法3 构建FP树4 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模…...
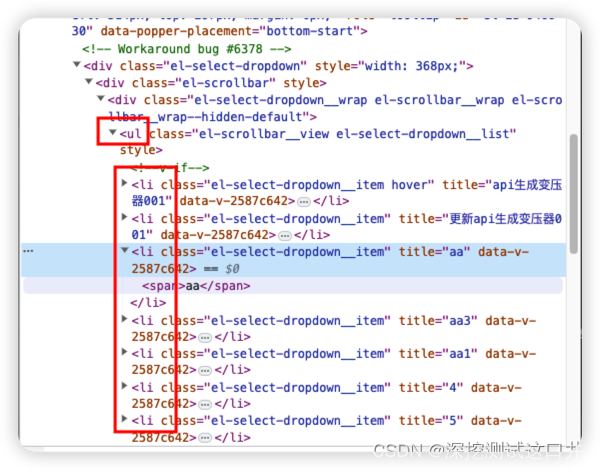
selenium 选定ul-li下拉选项中某个指定选项
场景:selenium的下拉选项是ul-li模式,选定某个指定的选项。 from selenium.webdriver.support.ui import WebDriverWait from selenium.webdriver.support import expected_conditions as EC # 显示等待def select_li(self, text, *ul_locator):"…...

回归预测 | MATLAB实现FA-SVM萤火虫算法优化支持向量机多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现FA-SVM萤火虫算法优化支持向量机多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现FA-SVM萤火虫算法优化支持向量机多输入单输出回归预测(多指标,多图)效果一览基本介绍…...

使用pytorch 的Transformer进行中英文翻译训练
下面是一个使用torch.nn.Transformer进行序列到序列(Sequence-to-Sequence)的机器翻译任务的示例代码,包括数据加载、模型搭建和训练过程。 import torch import torch.nn as nn from torch.nn import Transformer from torch.utils.data im…...

解决element的select组件创建新的选项可多选且opitions数据源中有数据的情况下,回车不能自动选中创建的问题
前言 最近开发项目使用element-plus库内的select组件,其中有提供一个创建新的选项的用法,但是发现一些小问题,在此记录 版本 “element-plus”: “^2.3.9”, “vue”: “^3.3.4”, 问题 1、在options数据源中无数据的时候,在输入框…...
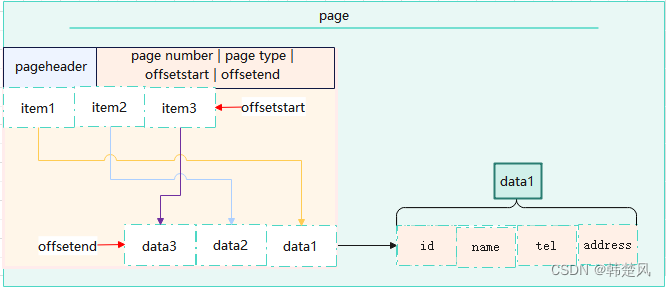
人工智能大模型加速数据库存储模型发展 行列混合存储下的破局
数据存储模型 专栏内容: postgresql内核源码分析手写数据库toadb并发编程toadb开源库 个人主页:我的主页 座右铭:天行健,君子以自强不息;地势坤,君子以厚德载物. 概述 在数据库的发展过程中,关…...
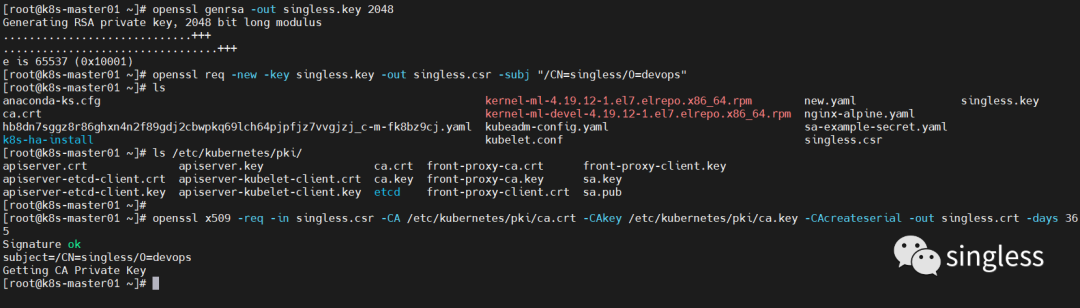
K8S用户管理体系介绍
1 K8S账户体系介绍 在k8s中,有两类用户,service account和user,我们可以通过创建role或clusterrole,再将账户和role或clusterrole进行绑定来给账号赋予权限,实现权限控制,两类账户的作用如下。 server acc…...
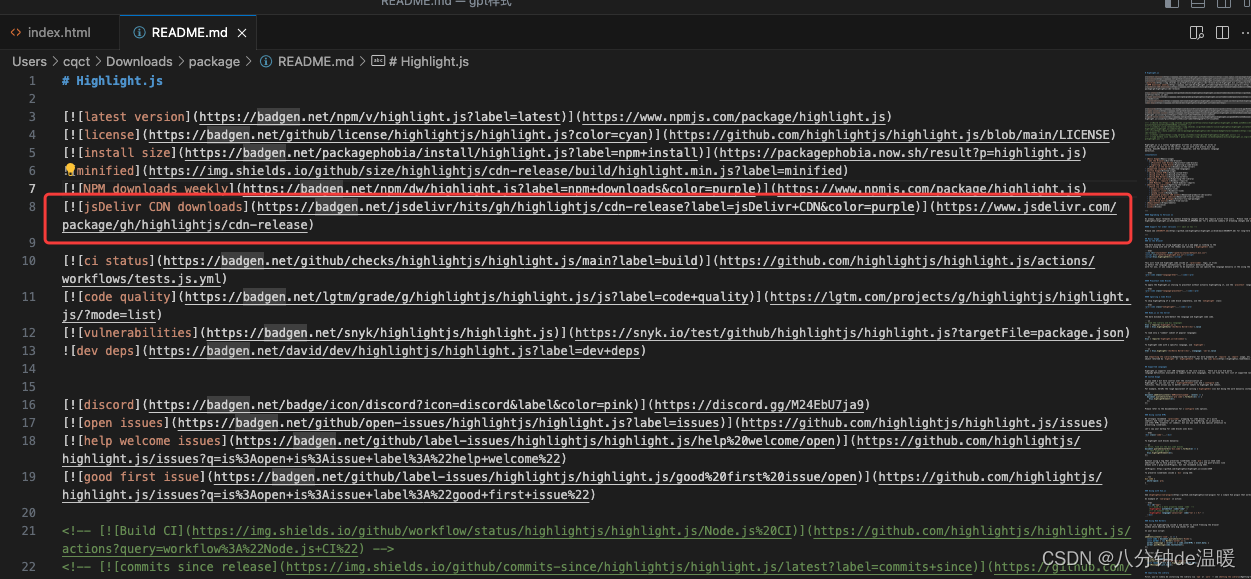
实现chatGPT 聊天样式
效果图 代码: <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Chat Example</title&g…...

day9 STM32 I2C总线通信
I2C总线简介 I2C总线介绍 I2C(Inter-Integrated Circuit)总线(也称IIC或I2C)是由PHILIPS公司开发的两线式串行总线,用于连接微控制器及其外围设备,是微电子通信控制领域广泛采用的一种总线标准。 它是同步通…...

终极Shell:Zsh(CentOS7 安装 zsh 及 配置 Oh my zsh)
CentOS7 安装 zsh 及 配置 Oh my zsh 我们在通过Shell操作linux终端时,配置、颜色区分、命令提示大都达不到我们预期的效果或者操作较为繁琐。 今天就来介绍一款终极一个及其好用的类Linux系统中的终端软件,江湖称之为马车中的跑车,跑车中的飞行车,史称『终极 Shell…...

Redis的数据持久化
前言 本文主要介绍Redis的三种持久化方式、AOF持久化策略等 什么是持久化 持久化是指将数据在内存中的状态保存到非易失性介质(如硬盘、固态硬盘等)上的过程。在计算机中,内存中的数据属于易失性数据,一旦断电或重启系统&#…...

CSS 选择器
前言 基础选择器 以下是几种常见的基础选择器。 标签选择器:通过HTML标签名称选择元素。 例如: p {color: red; } 上述样式规则将选择所有<p>标签 ,并将其文字颜色设置为红色。 类选择器:通过类名选择元素。使用类选择…...
)
上位机工作总结(2023.03-2023.08)
1.工作总结 不知不觉,已经从C#转为Qt开发快半年了。这半年内,也是学习了很多C相关的开发技能,同时自己的技术栈也是进一步丰富,以后跑路就更容易啦,哈哈!自己之前就有Winform和一些简单的Qt项目实践&#…...
APSIM模型参数优化 批量模拟丨气象数据准备、物候发育和光合生产、物质分配与产量模拟、土壤水分平衡算法、土壤碳氮平衡模块、农田管理模块等
随着数字农业和智慧农业的发展,基于过程的农业生产系统模型在模拟作物对气候变化的响应与适应、农田管理优化、作物品种和株型筛选、农田固碳和温室气体排放等领域扮演着越来越重要的作用。APSIM (Agricultural Production Systems sIMulator)模型是世界知名的作物生…...
Azure防火墙
文章目录 什么是Azure防火墙如何部署和配置创建虚拟网络创建虚拟机创建防火墙创建路由表,关联子网、路由配置防火墙策略配置应用程序规则配置网络规则配置 DNAT 规则 更改 Srv-Work 网络接口的主要和辅助 DNS 地址测试防火墙 什么是Azure防火墙 Azure防火墙是一种用…...
【LeetCode】剑指 Offer Ⅱ 第4章:链表(9道题) -- Java Version
题库链接:https://leetcode.cn/problem-list/e8X3pBZi/ 类型题目解决方案双指针剑指 Offer II 021. 删除链表的倒数第 N 个结点双指针 哨兵 ⭐剑指 Offer II 022. 链表中环的入口节点(环形链表)双指针:二次相遇 ⭐剑指 Offer I…...
Android SDK 上手指南|| 第三章 IDE:Android Studio速览
第三章 IDE:Android Studio速览 Android Studio是Google官方提供的IDE,它是基于IntelliJ IDEA开发而来,用来替代Eclipse。不过目前它还属于早期版本,目前的版本是0.4.2,每个3个月发布一个版本,最近的版本…...

Vue--》打造个性化医疗服务的医院预约系统(七)完结篇
今天开始使用 vue3 + ts 搭建一个医院预约系统的前台页面,因为文章会将项目的每一个地方代码的书写都会讲解到,所以本项目会分成好几篇文章进行讲解,我会在最后一篇文章中会将项目代码开源到我的GithHub上,大家可以自行去进行下载运行,希望本文章对有帮助的朋友们能多多关…...
点亮一颗LED灯
TOC LED0 RCC_APB2PeriphClockCmd(RCC_APB2Periph_GPIOB,ENABLE);//使能APB2的外设时钟GPIO_InitTypeDef GPIO_Initstructure;GPIO_Initstructure.GPIO_Mode GPIO_Mode_Out_PP;//通用推挽输出GPIO_Initstructure.GPIO_Pin GPIO_Pin_5;GPIO_Initstructure.GPIO_Speed GPIO_S…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
