数据结构之并查集
并查集
- 1. 并查集原理
- 2. 并查集实现
- 3. 并查集应用
- 3.1 省份数量
- 3.2 等式方程的可满足性
- 4. 并查集的优缺点及时间复杂度
1. 并查集原理
并查表原理是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。并查集的思想是用一个数组表示了整片森林(parent),树的根节点唯一标识了一个集合,我们只要找到了某个元素的树根,就能确定它在哪个集合里。这类问题的抽象数据类型称为并查集(union-find set)。
这个数据结构主要用于解决一些元素分组的问题,比如在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。
并查集怎样使用?并查集是用一个数组来进行表示,其中数组下标用来表示一个个体的编号, 数组中存的元素表示的是该个体在哪一个组,用组中的某个元素表示该组有多少个体。
并查集通常用-1进行初始化,为什么不用0/1…呢?这是因为数组中的元素代表的是该个体在哪一个组,如果用0/1进行初始化,那么如果某个个体是自己一个为一组,但并查集中所表示的又是该个体是0/1组的。
接下来举一个并查集的例子
比如:某天有一个班级需要进行分组完成任务,已知该班有10位同学,将其分成3组,每组分别有5、 3、 2位同学。现在给这些学生进行编号:{0,1,2,3,4,5,6,7,8,9},其中{0,5,7,8,9},{1,4,6},{2,3}分别是每组同学的编号,0,1,2分别是每组的组长。接下来用一个并查集来表示该结构。
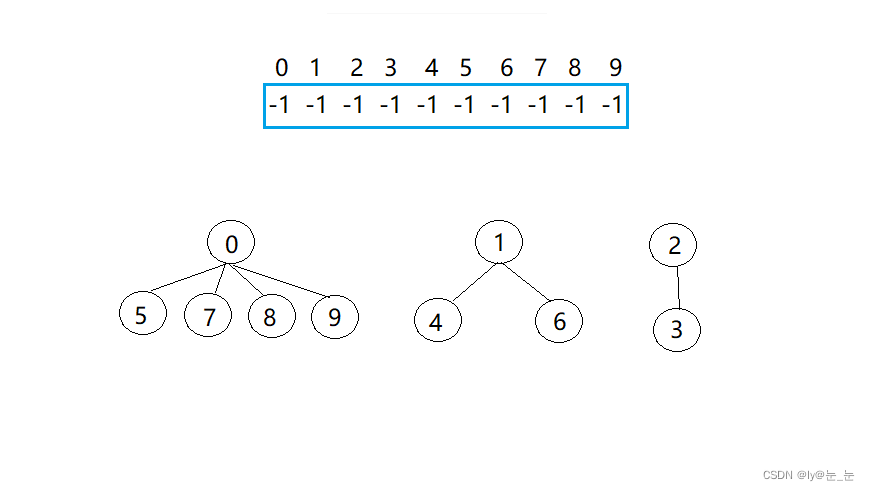
然后每收一个组员,就将该组员的元素加到组长下面,该组员存放的是组长的下边,如下图所示:0,1,2存放的绝对值就是每组成员的个数。
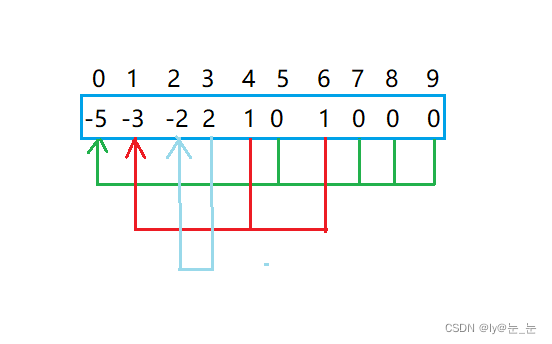
仔细观察数组中内的变化,可以得出以下结论:
- 数组的下标对应集合中元素的编号;
- 数组中如果为负数,负号代表根,数字代表该集合中元素个数;
- 数组中如果为非负数,代表该元素双亲在数组中的下标。
每个小组去做相似的任务,但是发现1组长和2组长所带领的小队进度较慢,时间又有些不够,于是让这两个小组合并,2组长任然是一个组长,这是比昂查表发生如下变化:
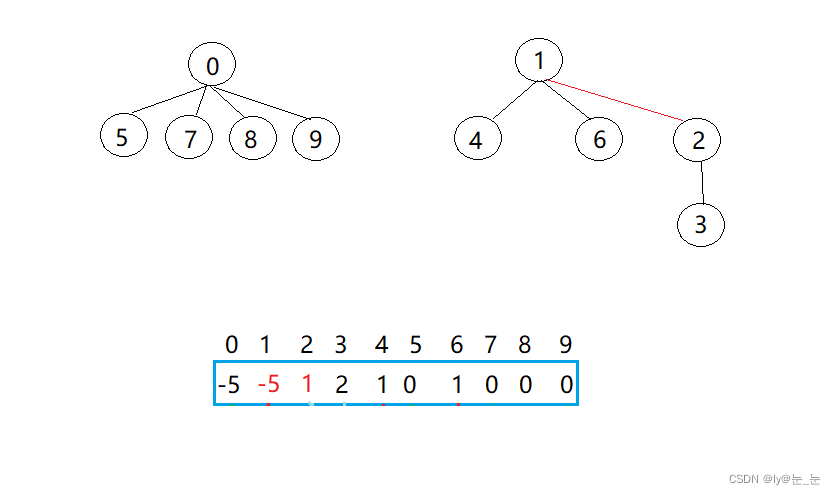
通过以上例子可知,并查集一般可以解决如下问题:
- 查找元素属于哪个集合:沿着数组表示树形关系以上一直找到根(即:树中中元素为负数的位置)
- 查看两个元素是否属于同一个集合:沿着数组表示的树形关系往上一直找到树的根,如果根相同表明在同一个集合,否则不在
- 将两个集合归并成一个集合:将两个集合中的元素合并,将一个集合名称改成另一个集合的名称
- 集合的个数:遍历数组,数组中元素为负数的个数即为集合的个数。
2. 并查集实现
接下来用代码来实现如上数据结构。
- 查找元素属于哪个集合
- 查看两个元素是否属于同一个集合
- 将两个集合归并成一个集合
- 集合的个数
#include <iostream>
#include <vector>
#include <assert.h>
using namespace std;class UnionFindSet
{
public:UnionFindSet(int size):_set(size, -1){}size_t FindRoot(int x) //1.查找元素属于哪个集合{assert(x < _set.size());while (_set[x] >= 0) //可能有两个集合合并,如上述两个组合并的例子;所以需要循环,找到小于0的下标x = _set[x];return x;}bool IsSameRoot(int x1, int x2) //2.查看两个元素是否属于同一个集合{int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (root1 == root2)return true;elsereturn false;}void Union(int x1, int x2) //3.将两个集合合并{int root1 = FindRoot(x1); //先找到两个集合各自的根int root2 = FindRoot(x2);if (root1 != root2) //如果根不相等,则将两个根进行合并{_set[root1] += _set[root2];_set[root2] = root1;}}size_t SetCount() //4.集合的个数{size_t count = 0;for (size_t i = 0; i < _set.size(); ++i){if (_set[i] < 0)++count;}return count;}
private:vector<int> _set;
};
测试代码如下:
void test()
{UnionFindSet st(10);st.Union(0, 5);st.Union(0, 7);st.Union(0, 8);st.Union(0, 9);st.Union(1, 4);st.Union(1, 6);st.Union(2, 3);cout << "4在集合:" << st.FindRoot(4) << endl;cout << "5和7是否在同一个集合中(0/1):" << st.IsSameRoot(5, 7) << endl;cout << "5和6是否在同一个集合中(0/1):" << st.IsSameRoot(5, 6) << endl;cout << "合并前集合的个数:" << st.SetCount() << endl;cout << "合并集合1和集合2" << endl;st.Union(1, 2);cout << "合并后集合的个数:" << st.SetCount() << endl;}
运行结果如下:
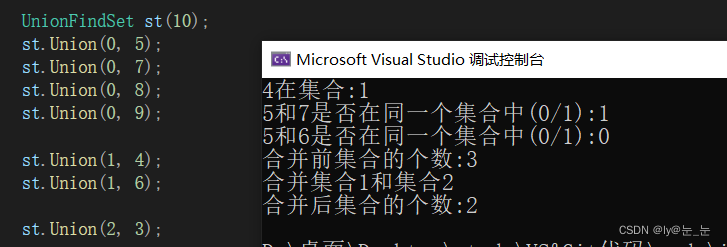
3. 并查集应用
3.1 省份数量
1.题目描述:有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
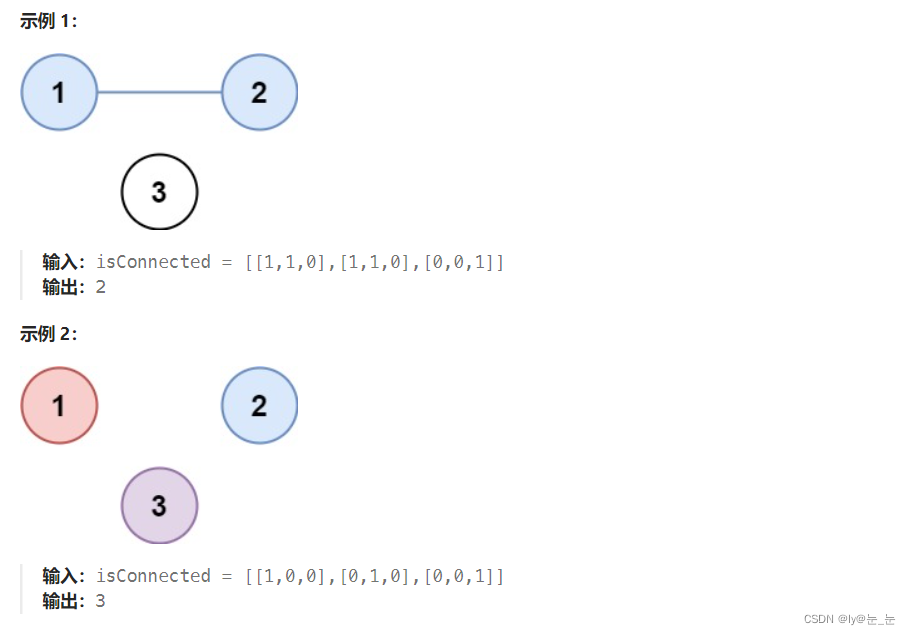
2.题目分析:可以用并查集来实现,对题目进行分析可以知道,要求集合的数量,所以需要上述3集合的合并函数和4集合的数量函数,其中3中又需要1函数,可以简单实现这几个函数,然后遍历题目中isConnected数组,只需要遍历一半即可。
3.代码如下:
class Solution {
public:size_t FindRoot(vector<int>& ufs, int x){while (ufs[x] >= 0)x = ufs[x];return x;}void Union(vector<int>& ufs, int x1, int x2){int root1 = FindRoot(ufs, x1);int root2 = FindRoot(ufs, x2);if (root1 != root2){ufs[root1] += ufs[root2];ufs[root2] = root1;}}size_t UfsCount(vector<int>& ufs){int count = 0;for (auto& x : ufs)if (x < 0)++count;return count;}int findCircleNum(vector<vector<int>>& isConnected){int n = isConnected.size();vector<int> ufs(n, -1);//合并相连的城市for (int i = 0; i < n; ++i){for (int j = i + 1; j < n; ++j){if (isConnected[i][j] == 1)Union(ufs, i, j);}}//寻找不相连省份的数量size_t count = UfsCount(ufs);return count;}
};
3.2 等式方程的可满足性
1.题目描述:给定一个由表示变量之间关系的字符串方程组成的数组,每个字符串方程 equations[i] 的长度为 4,并采用两种不同的形式之一:“a==b” 或 “a!=b”。在这里,a 和 b 是小写字母(不一定不同),表示单字母变量名。
只有当可以将整数分配给变量名,以便满足所有给定的方程时才返回 true,否则返回 false。
提示:
- <= equations.length <= 500
- equations[i].length == 4
- equations[i][0] 和 equations[i][3] 是小写字母
- equations[i][1] 要么是 ‘=’,要么是 ‘!’
- equations[i][2] 是 ‘=’

2.题目分析:这道题需要合并相等的字母,所以需要函数3和1,由题知equations[i][0] 和 equations[i][3] 是小写字母,所以开辟一个大小为26的数组,把相等的字母合并为一组,再寻找不相等的,如果不相等得两个字母有相同的根,则返回false。
3.代码如下:
class Solution {
public:size_t FindRoot(vector<int>& ufs, int x){while (ufs[x] >= 0)x = ufs[x];return x;}void Union(vector<int>& ufs, int x1, int x2){int root1 = FindRoot(ufs, x1);int root2 = FindRoot(ufs, x2);if (root1 != root2){ufs[root1] += ufs[root2];ufs[root2] = root1;}}bool equationsPossible(vector<string>& equations){vector<int> ufs(26, -1);// 把相等的值加到一个集合中for (auto& str : equations){if (str[1] == '='){Union(ufs, str[0] - 'a', str[3] - 'a');}}// 在遍历一遍,找不相等的,不相等的根一定在一个集合for (auto& str : equations){if (str[1] == '!'){int root1 = FindRoot(ufs, str[0] - 'a');int root2 = FindRoot(ufs, str[3] - 'a');if (root1 == root2){return false;}}}return true;}
};
4. 并查集的优缺点及时间复杂度
并查集这个数据结构的优缺点是
优点:
- 简单:并查集只需要一个一维数组来存储每个元素的父节点,操作也很简单,一般只需要两个基本函数:find和union。
- 高效:并查集的时间复杂度主要取决于树的高度,通过一些优化策略,如路径压缩和按秩合并,可以将树的高度控制在对数级别,从而实现近乎常数的查询和合并操作。
- 灵活:并查集可以用来解决各种涉及到元素分组、连通性、最小生成树等问题,可以根据具体问题进行扩展和修改。
缺点:
- 动态:并查集只能支持动态添加和合并元素,不能支持删除和分割元素,这限制了它的应用范围。
- 无序:并查集不能保证每个集合内部的元素是有序的,也不能提供遍历每个集合内部元素的方法,这使得它难以处理一些需要排序或遍历的问题。
- 单向:并查集只能判断两个元素是否属于同一个集合,不能判断两个元素之间的具体关系,如距离、方向、层次等,这使得它难以处理一些需要细节信息的问题。
时间复杂度
并查集的时间复杂度主要取决于树的高度,通过一些优化策略,如路径压缩和按秩合并,可以将树的高度控制在对数级别,从而实现近乎常数的查询和合并操作。具体来说:
初始化:O(n),其中n为元素个数。
查找:O(log n),其中n为元素个数。
合并:O(log n),其中n为元素个数。
相关文章:

数据结构之并查集
并查集 1. 并查集原理2. 并查集实现3. 并查集应用3.1 省份数量3.2 等式方程的可满足性 4. 并查集的优缺点及时间复杂度 1. 并查集原理 并查表原理是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。并查集的思想是用一个数组表示了整片森林࿰…...

[element-ui] el-date-picker a-range-picker type=“daterange“ rules 校验
项目场景: 在项目中表单提交有时间区间校验 问题描述 想当然的就和其他单个输入框字符串校验,导致提交保存的时候 ,初次日期未选择,规则提示。后续在同一表单上继续提交时,校验失效。走进了死胡同,一直以…...
Dockers搭建个人网盘、私有仓库,Dockerfile制作Nginx、Lamp镜像
目录 1、使用mysql:5.6和 owncloud 镜像,构建一个个人网盘。 (1)下载mysql:5.6和owncloud镜像 (2)创建启动mysql:5.6和owncloud容器 (3)在浏览器中输入网盘服务器的IP地址,进行账…...
)
2023 CCPC 华为云计算挑战赛 hdu7401 流量监控(树形dp)
题目 流量监控 - HDU 7401 - Virtual Judge 简单来说,T(T<20)组样例,sumn不超过2e4 每次给定一棵n(n<2000)个点的树,两问: ①将n个点恰拆成n/2个pair(u,v),要求一个点是另一个点的祖先,求方案数 …...
01.Django入门
1.创建项目 1.1基于终端创建Django项目 打开终端进入文件路径(打算将项目放在哪个目录,就进入哪个目录) E:\learning\python\Django 执行命令创建项目 F:\Anaconda3\envs\pythonWeb\Scripts\django-admin.exe(Django-admin.exe所…...
亿赛通电子文档安全管理系统任意文件上传漏洞(2023-HW)
亿赛通电子文档安全管理系统任意文件上传漏洞 一、 产品简介二、 漏洞概述三、 影响范围四、 复现环境五、 漏洞复现小龙POC检测 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果…...
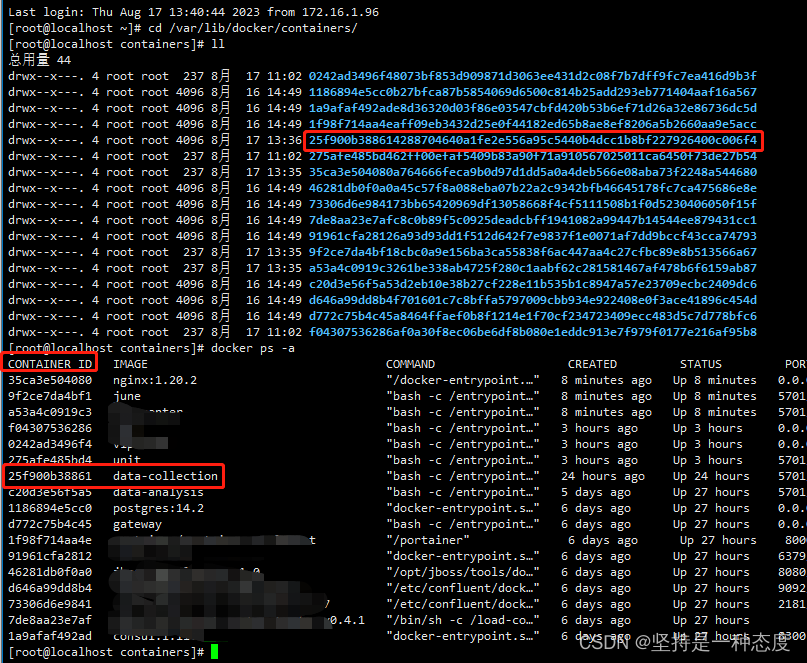
docker限制容器日志大小
文章目录 业务场景问题排查彻底解决 业务场景 我们公司做交通相关业务,我们部门主要负责信控服务,卖信号机的硬件产品和配套的信控平台 由于有部分小项目,可能只有几十个路口,客户预算有限,只给我们老旧的Windows ser…...

底层驱动实现数码管显示温湿度数值功能
开发板:STM32MP157A 温湿度传感器:si7006 显示器(数码管):m74hc595 遇到的问题:循环采集温湿度传感器数值,并将数值发送给数码管的时候两者存在竞态关系,导致数码管显示亮度很暗 …...

03架构管理之测试管理
专栏说明:针对于企业的架构管理岗位,分享架构管理岗位的职责,工作内容,指导架构师如何完成架构管理工作,完成架构师到架构管理者的转变。计划以10篇博客阐述清楚架构管理工作,专栏名称:架构管理…...
的知识)
30、devtools 依赖关于自动重启(自动加载页面)的知识
devtools 依赖关于自动重启的知识 ★ 自动重启 devtools会监控类加载路径中的文件(尤其是*.class文件),只要这些文件发生了改变, devtools就会自动重启Spring Boot应用。▲ 不同工具触发自动重启的方式:Eclipse&…...

ES6 Promise/Async/Await使用
Promise应用 在工作中, 我们经常会遇到用异步请求数据, 查询一个结果, 然后把返回的参数放入到下一个执行的异步函数像这样: $.ajax({..., success(resp)>{$.ajax({..., resp.id, success(resp)>{$.ajax({..., resp.name success(resp)>{//多层嵌套的情况, 看着是不…...
Word中对象方法(Methods)的理解及示例(上)
【分享成果,随喜正能量】奋斗没有终点,任何时候都是一个起点,沉潜是为了蓄势待发,沉潜是为了等待因缘。鲸豚沉潜于大海,幽兰深藏于山谷,能够经得起沉潜的人,才会有更高的成就。正如一年的树木只能当柴烧&am…...
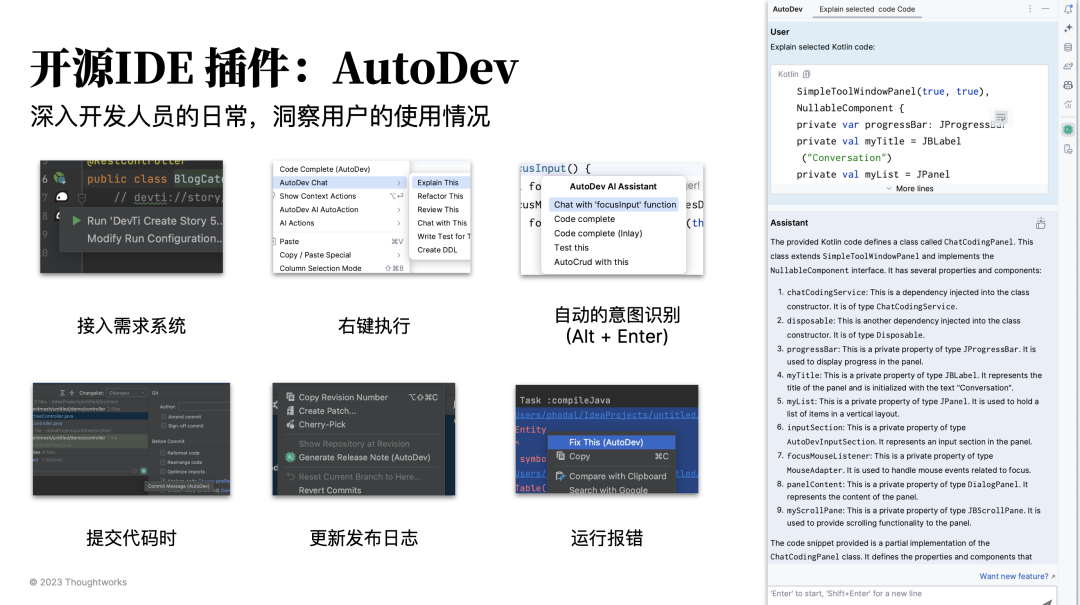
AutoDev 1.1.3 登场,个性化 AI 辅助:私有化大模型、自主设计 prompt、定义独特规则...
在过去的半个月里,我们为开源辅助编程工具 AutoDev 添加了更强大的自定义能力,现在你可以: 使用自己部署的开源大模型自己配置 Intellij IDEA 中的行为自定义开发过程中的规范 当然了,如果您自身拥有开发能力的话,建议…...

win11 python 调用edge调试过程
1、下载对应版本的驱动程序: https://developer.microsoft.com/zh-cn/microsoft-edge/tools/webdriver/ 2、和系统版本对应的exe文件(x86、x64要对应)放置的固定的目录,我放到了system32下了; 3、PATH路径添加windows/system32目录&#x…...

DS-排序回顾
快速排序相比于堆排序的优点有: 效率更高:快速排序的平均时间复杂度为 O(nlogn),而堆排序的时间复杂度为 O(nlogn)。虽然它们的时间复杂度相同,但是在实际情况下,快速排序往往比堆排序更快,因为快速排序具有…...
clion软件ide的安装和环境配置@ubuntu
1.官网: Download CLion 2.安装Clion 直接在官网下载并安装即可,过程很简单 https://www.jetbrains.com/clion/ https://www.jetbrains.com/clion/download/#sectionlinux 3.激活码 4.配置Clion 安装gcc、g、make Ubuntu中用到的编译工具是gcc©…...
Cpp学习——类与对象3
目录 一,初始化列表 1.初始化列表的使用 2.初始化列表的特点 3.必须要使用初始化列表的场景 二,单参数构造函数的隐式类型转换 1.内置类型的隐式类型转换 2. 自定义类型的隐式类型转换 3.多参数构造函数的隐式类型转换 4.当你不想要发生隐式类型转换…...

回归预测 | MATLAB实现PSO-RBF粒子群优化算法优化径向基函数神经网络多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现PSO-RBF粒子群优化算法优化径向基函数神经网络多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现PSO-RBF粒子群优化算法优化径向基函数神经网络多输入单输出回归预测(多指标,多图&a…...
)
ahooks.js:一款强大的React Hooks库及其API使用教程(四)
一、ahooks.js简介二、ahooks.js安装三、继续ahooks.js API的介绍与使用教程51. useResetState52. useUpdateLayoutEffect53. useDeepCompareLayoutEffect54. useRafInterval55. useRafTimeout56. useTimeout57. useLockFn58. useDocumentVisibility59. useDrop60. useDrag 一、…...

FOSSASIA Summit 2023 - 开源亚洲行
作者 Ted 致歉:本来这篇博客早就该发出,但是由于前几个月频繁差旅导致精神不佳,再加上后续我又参加了 Linux 基金会 7/27 在瑞士日内瓦举办的 Open Source Congress,以及 7/29-30 台北的 COSCUP23,干脆三篇连发&#x…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
