管理类联考——逻辑——真题篇——按知识分类——汇总篇——二、论证逻辑——支持加强——第三节——分类3——类比题干支持
文章目录
- 第三节 支持加强-分类3-类比题干支持
- 真题(2017-28)-支持加强-正面支持-表达“确实如此”
- 真题(2017-36)-支持加强-正面支持-表达“确实如此”
- 真题(2017-39)-支持加强-正面支持-方法有效或方法可行,但多半不选择方法无恶果
- 真题(2017-50)-支持加强
- 真题(2018-28)-支持加强
- 真题(2019-34)-支持加强
- 真题(2019-44)-支持加强
- 真题(2019-45)-支持加强
- 真题(2019-29)-支持加强
- 真题(2019-51)-支持加强
- 真题(2013-34)-可能性推理中的加强型题目
- 真题(2017-32)-支持加强
- 真题(
相关文章:

管理类联考——逻辑——真题篇——按知识分类——汇总篇——二、论证逻辑——支持加强——第三节——分类3——类比题干支持
文章目录 第三节 支持加强-分类3-类比题干支持真题(2017-28)-支持加强-正面支持-表达“确实如此”真题(2017-36)-支持加强-正面支持-表达“确实如此”真题(2017-39)-支持加强-正面支持-方法有效或方法可行,但多半不选择方法无恶果真题(2017-50)-支持加强真题(2018-2…...

搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nums[1], …, …...

Steam搬砖项目:最长久稳定的副业!
项目应该大家都有听说话,但是细节问题,如何操作可能有些不是很清楚,今天在这里简单分享一下。 这个Steam搬砖项目主要赚钱汇率差和价值差,是一个细分领取的小项目。 不用引流,时间也是比较自由的,你可以兼…...
最小化安装移动云大云操作系统--BCLinux-R8-U8-Server-x86_64-230802版
CentOS 结束技术支持,转为RHEL的前置stream版本后,国内开源Linux服务器OS生态转向了开源龙蜥和开源欧拉两大开源社区,对应衍生出了一系列商用Linux服务器系统。BC-Linux V8.8是中国移动基于龙蜥社区Anolis OS 8.8版本深度定制的企业级X86服务…...

神经网络基础-神经网络补充概念-05-导数
概念 导数是微积分中的一个概念,用于描述函数在某一点的变化率。在数学中,函数的导数表示函数值随着自变量的微小变化而产生的变化量,即斜率或变化率。 假设有一个函数 f(x),其中 x 是自变量,y f(x) 是因变量。函数…...

kubernetes — 安装Ingress
1、 Ingress 1、安装-Nginx-Ingress kubectl apply -f https://raw.githubusercontent.com/kubernetes/ingress-nginx/controller-v1.8.1/deploy/static/provider/cloud/deploy.yaml 2、设为默认的Ingress [rootk8s01 ~]# vim default_ingress.yaml apiVersion: networking.…...

SSR使用HTTPS
1.安装 npm i browser-sync 2. 再angular.json里配置 "serve-ssr": {"builder": "nguniversal/builders:ssr-dev-server","options": {"ssl": true,"sslCert": "./node_modules/browser-sync/certs/server…...

Spring Boot中使用validator如何实现接口入参自动检验
文章目录 一、背景二、使用三、举例 一、背景 在项目开发过程中,经常会对一些字段进行校验,比如字段的非空校验、字段的长度校验等,如果在每个需要的地方写一堆if else 会让你的代码变的冗余笨重且相对不好维护,如何更加规范和优…...

thinkphp 5 实现UNION ALL 3个联表查询,并且带上搜索条件,名称,时间,手机号
在ThinkPHP 5中实现带有搜索条件、名称、时间和手机号的3个联表查询(UNION ALL),您可以按照以下步骤进行操作: 确保已经配置好数据库连接信息和相关的模型。 使用union()方法来构建3个联表查询,同时在每个查询中添加所…...
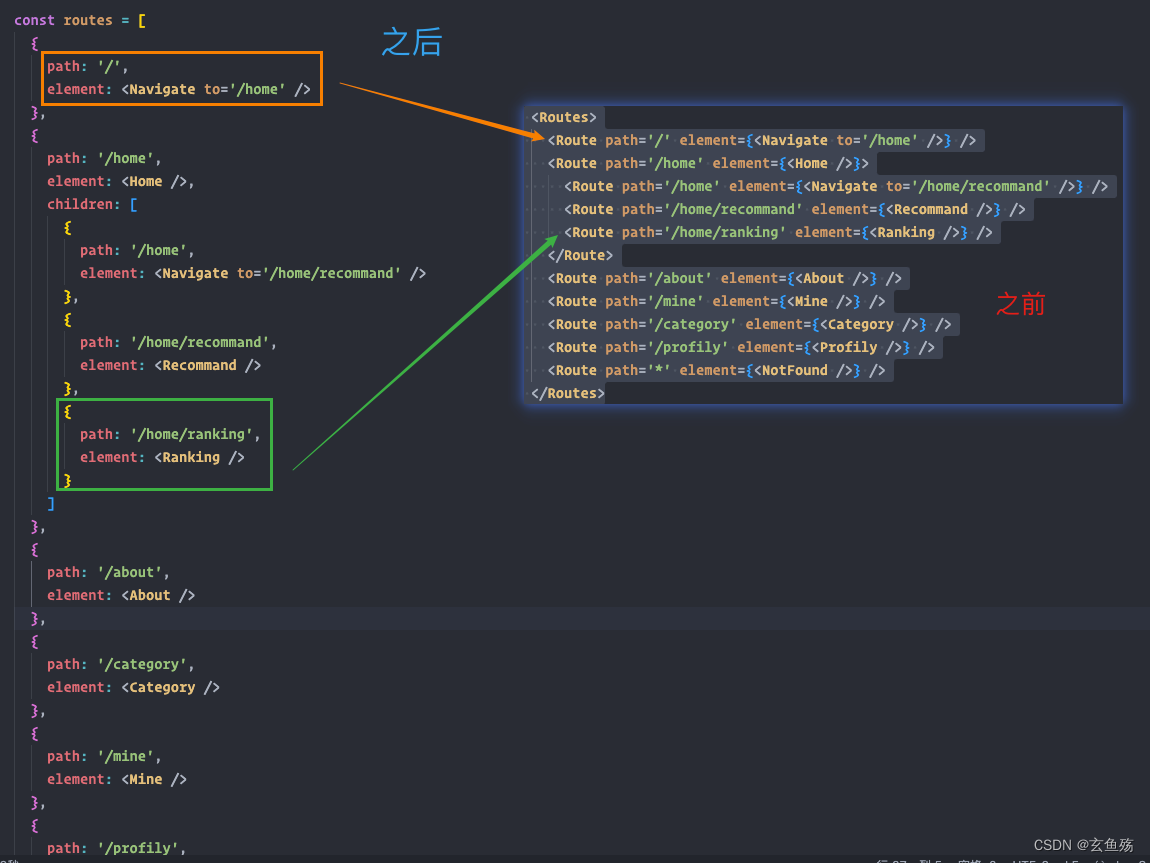
React 之 Router - 路由详解
一、Router的基本使用 1. 安装react-router react-router会包含一些react-native的内容,web开发并不需要 npm install react-router-dom 2. 设置使用模式 BrowserRouter或HashRouter Router中包含了对路径改变的监听,并且会将相应的路径传递给子组件Bro…...
框架分析(1)-IT人必须会
框架分析(1)-IT人必须会 专栏介绍当今主流框架前端框架后端框架移动应用框架数据库框架测试框架 Angular关键特点和功能:组件化架构双向数据绑定依赖注入路由功能强大的模板语法测试友好 优缺点分析优点缺点 总结 专栏介绍 link 主要对目前市…...
每天10个小知识点)
前端面试的游览器部分(7)每天10个小知识点
目录 系列文章目录前端面试的游览器部分(1)每天10个小知识点前端面试的游览器部分(2)每天10个小知识点前端面试的游览器部分(3)每天10个小知识点前端面试的游览器部分(4)每天10个小知…...

认识Junit
1. 前言 2. Junit注解 2.1. 常用的注解 2.1.1. Test 表示当前方法是一个测试方法(不需要main来执行) Test void Test01() throws InterruptedException {System.out.println("测试用例1");WebDriver webDriver new ChromeDriver();webDriver.get("https:/…...
Unity C# 引用池 ReferencePool
Unity C# 引用池 ReferencePool 1.目的 对于多次创建的数据使用new 关键字是十分消耗性能的,使用完成后由GC去自动释放,当一个类型的数据频繁创建可以使用引用池进行管理。 2.实现 项目目录 IReference 接口 要放入引用池的数据只需要继承这个接口…...
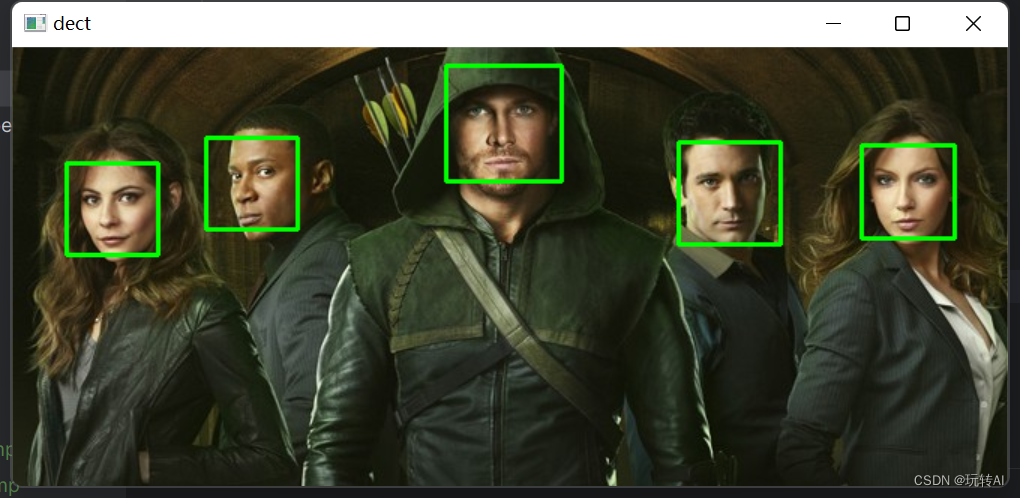
opencv 进阶10-人脸识别原理说明及示例-cv2.CascadeClassifier.detectMultiScale()
人脸识别是指程序对输入的人脸图像进行判断,并识别出其对应的人的过程。人脸识别程 序像我们人类一样,“看到”一张人脸后就能够分辨出这个人是家人、朋友还是明星。 当然,要实现人脸识别,首先要判断当前图像内是否出现了人脸&…...

〔013〕Stable Diffusion 之 图片自动评分和不健康内容过滤器 篇
✨ 目录 🎈 下载咖啡美学评价插件🎈 咖啡美学评价使用🎈 不健康内容过滤器插件🎈 下载咖啡美学评价插件 想让系统帮你的图片作品打分评价,可以下载咖啡美学自动评价插件插件地址:https://github.com/p1atdev/stable-diffusion-webui-cafe-aesthetic也可以通过扩展列表…...

6.RocketMQ之消费索引文件ConsumeQueue
功能:作为CommitLog文件的索引文件。 本文着重分析为consumequeue/topic/queueId目录下的索引文件。 1.ConsumeQueueStore public class ConsumeQueueStore {protected final ConcurrentMap<String>, ConcurrentMap<Integer>, ConsumeQueueInterface…...
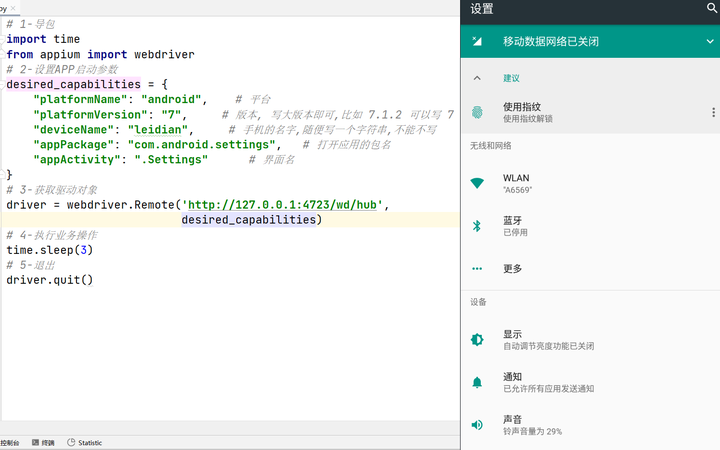
Appium-移动端自动测试框架,如何入门?
Appium是一个开源跨平台移动应用自动化测试框架。 既然只是想学习下Appium如何入门,那么我们就直奔主题。文章结构如下: 1、为什么要使用Appium? 2、如何搭建Appium工具环境?(超详细) 3、通过demo演示Appium的使用 4、Appium如何…...
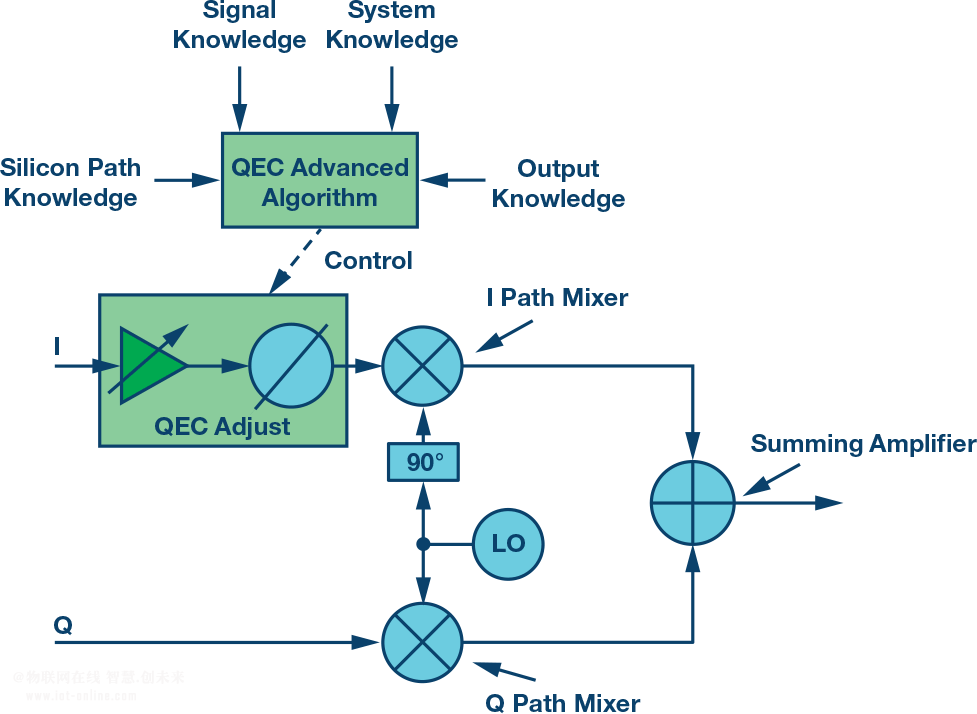
复数混频器、零中频架构和高级算法开发
文章里讲解了关于射频IQ调制器、零中频架构相关的原理及技术,全都是干货!其实好多同行对软件无线电的原理、IQ调制、镜像抑制都是一知半解,知其然不知其所以然。好好研读这篇文章,相信会让你有种恍然大悟的感觉。 RF工程常被视为…...
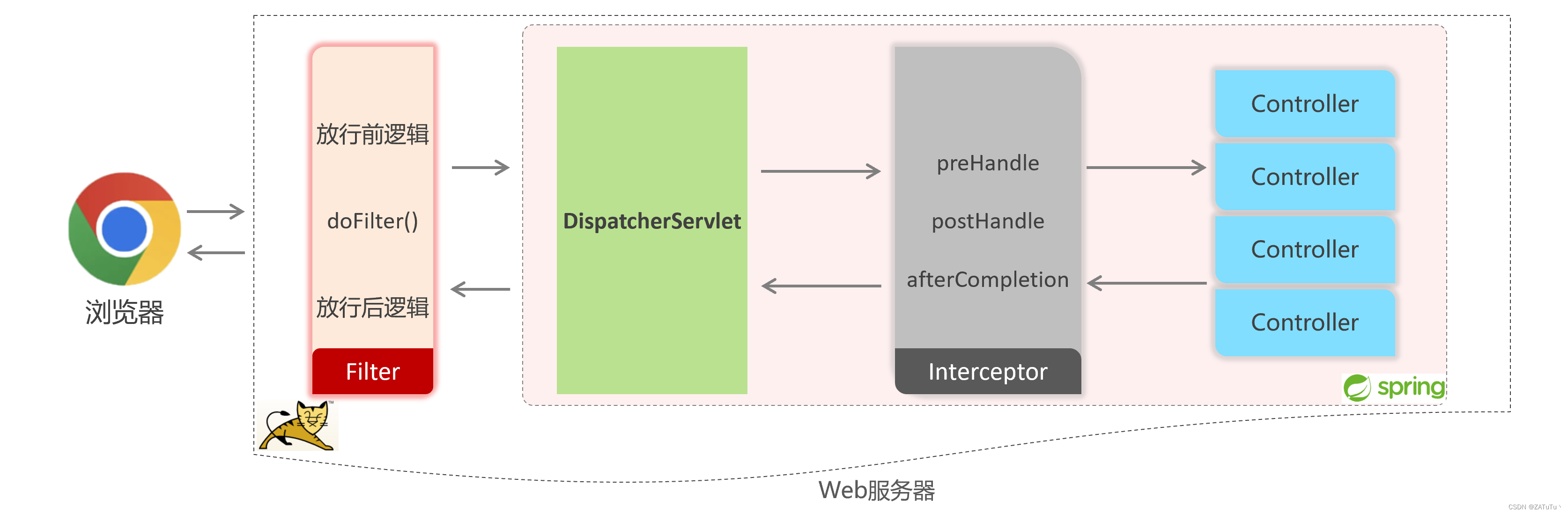
Web 拦截器-interceptor
拦截器是一种动态拦截方法调用的机制,类似于过滤器,是Spring框架提出的,用来动态拦截控制器方法的执行。 其作用是拦截请求,在指定方法调用前后,根据业务执行预设代码。 实现步骤 1.定义拦截器,实现Handl…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...
