第22次CCF计算机软件能力认证
第一题:灰度直方图
解题思路:
哈希表即可
#include<iostream>
#include<cstring>using namespace std;const int N = 610;
int a[N];
int n , m , l;int main()
{memset(a , 0 , sizeof a);cin >> n >> m >> l;for(int i = 0;i < n;i ++)for(int j = 0;j < m;j ++){int x;cin >> x;a[x] ++;}for(int i = 0;i < l;i ++)cout << a[i] << " ";return 0;
}第二题:邻域均值
解题思路:
二维前缀和
#include<iostream>
#include<cstring>using namespace std;const int N = 610;
int s[N][N];
int n , l , r , t;int main()
{memset(s , 0 , sizeof s);cin >> n >> l >> r >> t;for(int i = 1;i <= n;i ++)for(int j = 1;j <= n;j ++){int x;cin >> x;s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1] + x;}int res = 0;for(int i = 1;i <= n;i ++)for(int j = 1;j <= n;j ++){int x1 = max(1 , i - r) , y1 = max(1 , j - r);int x2 = min(n , i + r) , y2 = min(n , j + r);int sum = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];int cnt = (x2 - x1 + 1) * (y2 - y1 + 1);if(sum <= t * cnt) res ++;}cout << res << endl;return 0;
}第三题:DHCP服务器
解题思路:
认真读题,题目描述的非常清楚更具题目进行求解即可,
#include<iostream>
#include<algorithm>using namespace std;const int N = 1e5 + 10;int n , tdef , tmax , tmin;
string h; // 本机名称struct IP
{int st; // 0表示未分配、1表示待分配、2表示占用、3表示过期string owner; // 未分配状态没有占用者int t; // 待分配和占用状态拥有一个大于零的过期时刻
}ip[N];int get_ip_d(string c)
{for(int i = 1;i <= n;i ++)if(ip[i].owner == c) return i;return 0;
}int get_ip(int state)
{/*若没有,则选取最小的状态为未分配的 IP 地址若没有,则选取最小的状态为过期的 IP 地址*/for(int i = 1;i <= n;i ++)if(ip[i].st == state) return i;return 0;
}void update(string send)
{/*若不是,则找到占用者为发送主机的所有 IP 地址,对于其中状态为待分配的,将其状态设置为未分配,并清空其占用者,清零其过期时刻,处理结束*/for(int i = 1;i <= n;i ++)if(ip[i].owner == send) {if(ip[i].st == 1){ip[i].st = 0;ip[i].owner = "";ip[i].t = 0;}}
}void change(int tc)
{/*在到达该过期时刻时,若该地址的状态是待分配,则该地址的状态会自动变为未分配,且占用者清空,过期时刻清零;否则该地址的状态会由占用自动变为过期,且过期时刻清零。*/for(int i = 1;i <= n;i ++)if(ip[i].t && ip[i].t <= tc){if (ip[i].st == 1){ip[i].st = 0;ip[i].owner = "";ip[i].t = 0;}else{ip[i].st = 3;ip[i].t = 0;}}
}int main()
{cin >> n >> tdef >> tmax >> tmin >> h;int q;cin >> q;while(q --){// <发送主机> <接收主机> <报文类型> <IP 地址> <过期时刻>string send , get , type;int x , tc , te;cin >> tc >> send >> get >> type >> x >> te;if(get != h && get != "*") {// 判断接收主机是否为本机,或者为 *,若不是,则判断类型是否为 Request,若不是,则不处理;if(type != "REQ") continue; }// 若类型不是 Discover、Request 之一,则不处理if(type != "REQ" && type != "DIS") continue;// 若接收主机为 *,但类型不是 Discover,或接收主机是本机,但类型是 Discover,则不处理。if(get == "*" && type != "DIS" || get == h && type == "DIS") continue;change(tc);// discover 报文if(type == "DIS"){int k = get_ip_d(send);if(!k) k = get_ip(0);if(!k) k = get_ip(3);if(!k) continue;// 将该 IP 地址状态设置为待分配,占用者设置为发送主机ip[k].st = 1 , ip[k].owner = send;// 若报文中过期时刻为 0 ,则设置过期时刻为 t+tdefif(!te) ip[k].t = tc + tdef;else{int w = te - tc;w = min(w , tmax) , w = max(w , tmin);ip[k].t = w + tc;}cout << h << " " << send << " OFR " << k << " " << ip[k].t << endl;}else{if(get != h) {update(send);continue;}if(!(x <= n && x >= 1 && ip[x].owner == send)){cout << h << " " << send << " NAK " << x << " " << 0 << endl;continue;}// 无论该 IP 地址的状态为何,将该 IP 地址的状态设置为占用ip[x].st = 2;if (!te) ip[x].t = tc + tdef;else{int w = te - tc;w = max(w , tmin), w = min(w, tmax);ip[x].t = tc + w;}cout << h << " " << send << " ACK " << x << " " << ip[x].t << endl;}}return 0;
}第四题:校门外的树
解题思路:
dp问题
设 f[i] 为用了前 i 个障碍点的所有方案
f[i]=(f[0]∗cnt1+f[1]∗cnt2+…+f[j]∗cnt3+…+f[i−1]∗cnt(i−1))
f[i] 在循环的时候已经计算出结果,计算cnt值为重中之重
cnt值,也就是两个位置之间可以整除的结果个数,也就是约数个数。
#include<iostream>
#include<cstring>
#include<unordered_map>
#include<vector>using namespace std;const int N = 1010 , M = 1e5 + 10 , mod = 1e9 + 7;
int n;
int a[N] , f[N];
unordered_map<int , vector<int>>mp;
bool st[M];int main()
{for(int i = 1;i < M;i ++)for(int j = i * 2;j < M;j += i)mp[j].push_back(i); // 枚举因数cin >> n;for(int i = 0;i < n;i ++) cin >> a[i];f[0] = 1;for(int i = 1;i < n;i ++){memset(st , 0 , sizeof st);for(int j = i - 1;j >= 0;j --){int d = a[i] - a[j] , cnt = 0;for(int k : mp[d])if(!st[k]){cnt ++;st[k] = true;}st[d] = true;f[i] = (f[i] + (long long)f[j] * cnt) % mod;}}cout << f[n - 1] << endl;return 0;
}第五题:疫苗运输
迪杰斯特拉+扩展欧几里得算法
(不会)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>#define x first
#define y secondusing namespace std;typedef long long LL;
typedef pair<int, int> PII;const int N = 510;
const LL INF = 0x3f3f3f3f3f3f3f3fll;int n, m;
int len[N];
struct Node
{int cid, sum, pid;
};
vector<Node> ps[N];
vector<PII> line[N]; // x表示节点编号;y表示到下一个点的距离
LL dist[N], ans[N];
int pid[N];
bool st[N];LL exgcd(LL a, LL b, LL &x, LL &y) // 扩展欧几里得算法, 求x, y,使得ax + by = gcd(a, b)
{if (!b){x = 1; y = 0;return a;}LL d = exgcd(b, a % b, y, x);y -= (a / b) * x;return d;
}void dijkstra()
{memset(dist, 0x3f, sizeof dist);for (int i = 0; i < m; i ++ ){int d = 0;for (int j = 0; j < line[i].size(); j ++ ){if (line[i][j].x == 1){dist[i] = d;pid[i] = j;break;}d += line[i][j].y;}}for (int i = 0; i < m; i ++ ){int t = -1;for (int j = 0; j < m; j ++ )if (!st[j] && (t == -1 || dist[j] < dist[t]))t = j;st[t] = true;auto& l = line[t];auto d = dist[t];for (int j = pid[t], k = 0; k < l.size(); j = (j + 1) % l.size(), k ++ ){for (auto& c: ps[l[j].x]){if (st[c.cid]) continue; // 优化很重要LL a = d, b = len[t];LL x = c.sum, y = len[c.cid];LL X, Y;LL D = exgcd(b, y, X, Y);if ((x - a) % D) continue;X = (x - a) / D * X;y /= D;X = (X % y + y) % y;if (dist[c.cid] > a + b * X){dist[c.cid] = a + b * X;pid[c.cid] = c.pid;}}d += l[j].y;}}
}int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < m; i ++ ){int cnt, sum = 0;scanf("%d", &cnt);for (int j = 0; j < cnt; j ++ ){int ver, t;scanf("%d%d", &ver, &t);ps[ver].push_back({i, sum, j});line[i].push_back({ver, t});sum += t;}len[i] = sum;}dijkstra();memset(ans, 0x3f, sizeof ans);for (int i = 0; i < m; i ++ ){if (dist[i] == INF) continue;LL d = dist[i];for (int j = pid[i], k = 0; k < line[i].size(); j = (j + 1) % line[i].size(), k ++ ){int ver = line[i][j].x;ans[ver] = min(ans[ver], d);d += line[i][j].y;}}for (int i = 2; i <= n; i ++ )if (ans[i] == INF) puts("inf");else printf("%lld\n", ans[i]);return 0;
}
相关文章:

第22次CCF计算机软件能力认证
第一题:灰度直方图 解题思路: 哈希表即可 #include<iostream> #include<cstring>using namespace std;const int N 610; int a[N]; int n , m , l;int main() {memset(a , 0 , sizeof a);cin >> n >> m >> l;for(int …...
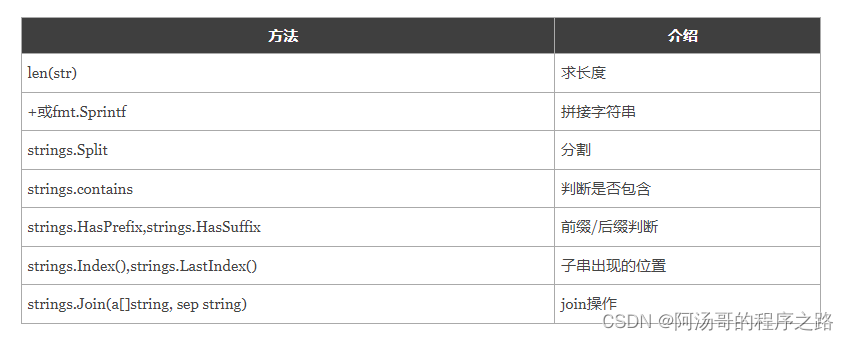
Go语言基础之基本数据类型
Go语言中有丰富的数据类型,除了基本的整型、浮点型、布尔型、字符串外,还有数组、切片、结构体、函数、map、通道(channel)等。Go 语言的基本类型和其他语言大同小异。 基本数据类型 整型 整型分为以下两个大类: 按…...

Linux Tracing Technologies
目录 1. Linux Tracing Technologies 1. Linux Tracing Technologies Linux Tracing TechnologieseBPFXDPDPDK...

iOS自定义下拉刷新控件
自定义下拉刷新控件 概述 用了很多的别人的下拉刷新控件,想写一个玩玩,自定义一个在使用的时候也会比较有意思。使应用更加的灵动一些,毕竟谁不喜欢各种动画恰到好处的应用呢。 使用方式如下: tableview.refreshControl XRef…...
Springboot写单元测试
导入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-test</artifactId><exclusions><exclusion><groupId>org.junit.vintage</groupId><artifactId>junit-vintag…...
一篇文章教你使用Docker本地化部署Chatgpt(非api,速度非常快!!!)及裸连GPT的方式(告别镜像GPT)
本地搭建ChatGPT(非api调用) 第一种方法:使用Docker本地化部署第一步,下载安装Docker登录GPT 第二种方法:不部署项目,直接连接 第一种方法:使用Docker本地化部署 这种方法的好处就是没有登录限…...
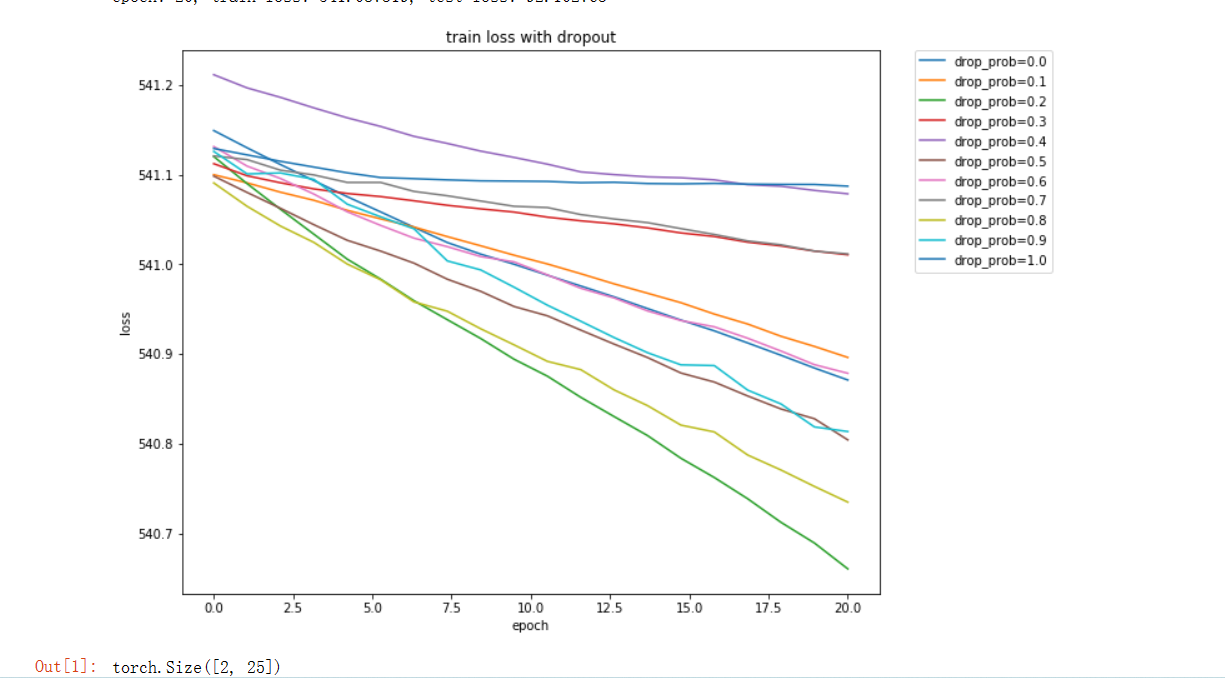
前馈神经网络dropout实例
直接看代码。 (一)手动实现 import torch import torch.nn as nn import numpy as np import torchvision import torchvision.transforms as transforms import matplotlib.pyplot as plt#下载MNIST手写数据集 mnist_train torchvision.datasets.MN…...
Android DataStore:安全存储和轻松管理数据
关于作者:CSDN内容合伙人、技术专家, 从零开始做日活千万级APP。 专注于分享各领域原创系列文章 ,擅长java后端、移动开发、人工智能等,希望大家多多支持。 目录 一、导读二、概览三、使用3.1 Preferences DataStore添加依赖数据读…...

opencv进阶12-EigenFaces 人脸识别
EigenFaces 通常也被称为 特征脸,它使用主成分分析(Principal Component Analysis,PCA) 方法将高维的人脸数据处理为低维数据后(降维),再进行数据分析和处理,获取识别结果。 基本原理…...

The internal rate of return (IRR)
内部收益率 NPV(Net Present Value)_spencer_tseng的博客-CSDN博客...

半导体自动化专用静电消除器主要由哪些部分组成
半导体自动化专用静电消除器是一种用于消除半导体生产过程中的静电问题的设备。由于半导体制造过程中对静电的敏感性,静电可能会对半导体器件的质量和可靠性产生很大的影响,甚至造成元件损坏。因此,半导体生产中采用专用的静电消除器是非常重…...

【C++入门到精通】C++入门 —— deque(STL)
阅读导航 前言一、deque简介1. 概念2. 特点 二、deque使用1. 基本操作(增、删、查、改)2. 底层结构 三、deque的缺陷四、 为什么选择deque作为stack和queue的底层默认容器总结温馨提示 前言 文章绑定了VS平台下std::deque的源码,大家可以下载…...

Codeforces Round 893 (Div. 2) D.Trees and Segments
原题链接:Problem - D - Codeforces 题面: 大概意思就是让你在翻转01串不超过k次的情况下,使得a*(0的最大连续长度)(1的最大连续长度)最大(1<a<n)。输出n个数&…...
SpringBoot + Vue 前后端分离项目 微人事(九)
职位管理后端接口设计 在controller包里面新建system包,再在system包里面新建basic包,再在basic包里面创建PositionController类,在定义PositionController类的接口的时候,一定要与数据库的menu中的url地址到一致,不然…...

【业务功能篇71】Cglib的BeanCopier进行Bean对象拷贝
选择Cglib的BeanCopier进行Bean拷贝的理由是, 其性能要比Spring的BeanUtils,Apache的BeanUtils和PropertyUtils要好很多, 尤其是数据量比较大的情况下。 BeanCopier的主要作用是将数据库层面的Entity转化成service层的POJO。BeanCopier其实已…...
让eslint的错误信息显示在项目界面上
1.需求描述 效果如下 让eslint中的错误,显示在项目界面上 2.问题解决 1.安装 vite-plugin-eslint 插件 npm install vite-plugin-eslint --save-dev2.配置插件 // vite.config.js import { defineConfig } from vite import vue from vitejs/plugin-vue import e…...
手摸手带你实现一个开箱即用的Node邮件推送服务
目录 编辑 前言 准备工作 邮箱配置 代码实现 服务部署 使用效果 题外话 写在最后 相关代码: 前言 由于邮箱账号和手机号的唯一性,通常实现验证码的校验时比较常用的两种方式是手机短信推送和邮箱推送,此外,邮件推送服…...

【Linux网络】网络编程套接字 -- 基于socket实现一个简单UDP网络程序
认识端口号网络字节序处理字节序函数 htonl、htons、ntohl、ntohs socketsocket编程接口sockaddr结构结尾实现UDP程序的socket接口使用解析socket处理 IP 地址的函数初始化sockaddr_inbindrecvfromsendto 实现一个简单的UDP网络程序封装服务器相关代码封装客户端相关代码实验结…...
)
Python学习笔记第六十四天(Matplotlib 网格线)
Python学习笔记第六十四天 Matplotlib 网格线普通网格线样式网格线 后记 Matplotlib 网格线 我们可以使用 pyplot 中的 grid() 方法来设置图表中的网格线。 grid() 方法语法格式如下: matplotlib.pyplot.grid(bNone, whichmajor, axisboth, )参数说明:…...
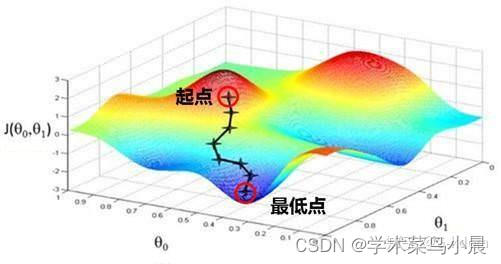
机器学习与模式识别3(线性回归与逻辑回归)
一、线性回归与逻辑回归简介 线性回归主要功能是拟合数据,常用平方误差函数。 逻辑回归主要功能是区分数据,找到决策边界,常用交叉熵。 二、线性回归与逻辑回归的实现 1.线性回归 利用回归方程对一个或多个特征值和目标值之间的关系进行建模…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
