机器人的运动范围
声明
该系列文章仅仅展示个人的解题思路和分析过程,并非一定是优质题解,重要的是通过分析和解决问题能让我们逐渐熟练和成长,从新手到大佬离不开一个磨练的过程,加油!
原题链接
机器人的运动范围![]() https://leetcode.cn/leetbook/read/illustration-of-algorithm/9h6vo2/
https://leetcode.cn/leetbook/read/illustration-of-algorithm/9h6vo2/
算法分析

图1是机器人移动范围的网格,结合题目的描述,我们来确定变量和逻辑主体。
(1)变量:设网格的行数为m,列数为n,移动限定值为k,设单元格坐标为(x,y),[x]表示x的数位之和,[y]同理,可达坐标个数sum,已探索坐标列表list。
(2)特殊描述:
①k是用于判断移动是否合理的值,要求[x]+[y] <= k;
②数位之和:如数字45,[45]=4+5=9;
③移动方向分为上下左右,不可越界;
④起点为(0,0),1 <= m <= 100,1 <= n <= 100,0 <= k <= 20;
(3)求取[x]:
①x < 10,[x] = x;
②x >= 10,[x] = x - (x / 10) * 9;
(4)越界判断:
单元格坐标为(x,y),x属于[0,M-1],y属于[0,N-1],若x或y均满足指定取值范围则表明未越界,反之则越界。
(5)机器人移动:
传入行数、列数、当前坐标、移动限定值、可达解个数、已访问的坐标值列表。检测当前坐标是否越界,若越界则return;检测当前坐标数位和是否满足条件,若不满足则return;检测当前坐标是否重复访问,若重复访问则return;三种情况均不满足则将当前坐标添加至已访问列表中,然后继续尝试往上下左右四个方向进行移动,重复上述过程。
(6)定义一个坐标值数据结构:
用于记录横纵坐标、比较坐标以及生成基于当前坐标指定方向的坐标值。
代码示例(C#)
//主方法
public int MovingCount(int m, int n, int k)
{if (m <= 0 || n <= 0 || k < 0) return 0;int sum = 0;List<Vector2> list = new();Search(m, n, new(0, 0), k, ref sum, ref list);return sum;
}//移动方向的枚举值
private enum Direction
{unknown, left, right, up, down
}//坐标值数据结构
private struct Vector2
{public int x;//横坐标public int y;//纵坐标public Vector2(int x, int y){this.x = x;this.y = y;}//比较方法public bool CompareTo(Vector2 vector){return x == vector.x && y == vector.y;}//生成基于当前坐标指定方向的坐标值public Vector2 Generate(Direction direction){return direction switch{Direction.left => new Vector2(x - 1, y),Direction.right => new Vector2(x + 1, y),Direction.up => new Vector2(x, y + 1),Direction.down => new Vector2(x, y - 1),_ => new Vector2(x, y),};}
}//坐标搜索方法
//参数:行数、列数、坐标值、移动限定值、可达解个数、已访问的坐标值列表
private void Search(int m, int n, Vector2 vector, int k, ref int sum, ref List<Vector2> list)
{//越界检测if (vector.x < 0 || vector.x >= m || vector.y < 0 || vector.y >= n) return;//当前坐标的数位和检测if (DigitalSum(vector.x) + DigitalSum(vector.y) > k) return;//重复访问检测if (list.Exists(vec => vec.CompareTo(vector))) return;list.Add(vector);sum++;//生成当前坐标的四个方向的坐标值Vector2[] vectors ={vector.Generate(Direction.left),vector.Generate(Direction.right),vector.Generate(Direction.up),vector.Generate(Direction.down)};//搜索四个方向的坐标Search(m, n, vectors[0], k, ref sum, ref list);Search(m, n, vectors[1], k, ref sum, ref list);Search(m, n, vectors[2], k, ref sum, ref list);Search(m, n, vectors[3], k, ref sum, ref list);
}//计算指定值的数位和
private int DigitalSum(int val)
{if (val < 10) return val;return val - (val / 10) * 9;
}算法解说
根据题目要求我们需要通过一个网格来模拟机器人的移动范围,并且我们对机器人可移动的单元格进行了限定,我们从左至右和从上至下分别从小到大对坐标进行划分,如此我们便可以唯一确定每一个单元格,如图1所示。坐标除了用于记录位置信息外我们还需要它提供一些特殊的方法,例如CompareTo和Generate,这两个方法分别用于比较坐标和生成基于当前坐标指定方向的坐标,因此我们应该把它单独为一个类。
其次就是我们搜索机器人移动路径的主要方法了,可以先尝试模拟一下,我们从起始点出发,拥有四个可移动的方向,但是这就存在三个特殊情况,,所以我们需要对每个坐标进行判断,第一需要考虑这个坐标是否越界,第二需要考虑这个坐标是否受到移动限定值的影响,第三需要考虑这个坐标是否已经探索过,只有当以上三个情况均不满足的时候,才应该记录为允许移动的坐标。
如何将算法分析转换为代码,依旧是确定两个点,一是变量,二是逻辑主体,结合算法分析中的描述即可确定我们需要定义哪些变量以及逻辑主体是什么。
相关文章:

机器人的运动范围
声明 该系列文章仅仅展示个人的解题思路和分析过程,并非一定是优质题解,重要的是通过分析和解决问题能让我们逐渐熟练和成长,从新手到大佬离不开一个磨练的过程,加油! 原题链接 机器人的运动范围https://leetcode.c…...
学习笔记|基于Delay实现的LED闪烁|模块化编程|SOS求救灯光|STC32G单片机视频开发教程(冲哥)|第六集(下):实现LED闪烁
文章目录 2 函数的使用1.函数定义(需要带类型)2.函数声明(需要带类型)3.函数调用 3 新建文件,使用模块化编程新建xxx.c和xxx.h文件xxx.h格式:调用头文件验证代码调用:完整的文件结构如下&#x…...
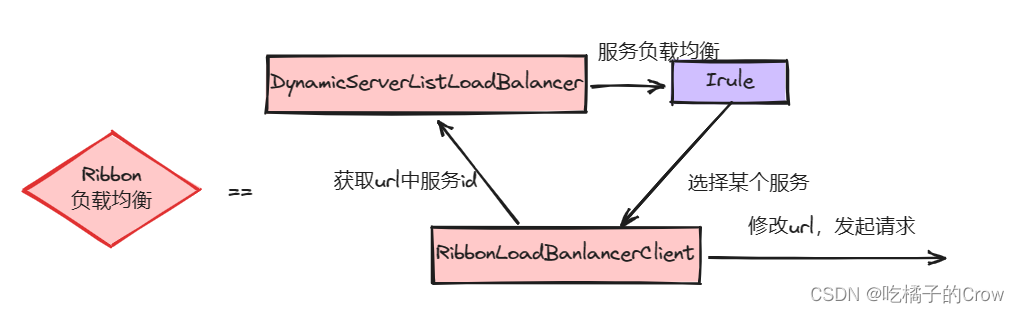
微服务-Ribbon(负载均衡)
负载均衡的面对多个相同的服务的时候,我们选择一定的策略去选择一个服务进行 负载均衡流程 Ribbon结构组成 负载均衡策略 RoundRobinRule:简单的轮询服务列表来选择服务器AvailabilityFilteringRule 对两种情况服务器进行忽略: 1.在默认情…...
解决C#报“MSB3088 未能读取状态文件*.csprojAssemblyReference.cache“问题
今天在使用vscode软件C#插件,编译.cs文件时,发现如下warning: 图(1) C#报cache没有更新 出现该warning的原因:当前.cs文件修改了,但是其缓存文件*.csprojAssemblyReference.cache没有更新,需要重新清理一下工程&#x…...
GeoScene Pro在地图制图当中的应用
任何地理信息系统建设过程中,背景地图的展示效果对整个系统功能的实现没有直接影响;但是地图的好看与否,会间接的决定着整个项目的高度。 一幅精美的地图不仅能令人赏心悦目、眼前一亮,更能将人吸引到你的系统中,更愿意…...

国标混凝土结构设计规范的混凝土本构关系——基于python代码生成
文章目录 0. 背景1. 代码2. 结果测试 0. 背景 最近在梳理混凝土塔筒的计算指南,在求解弯矩曲率关系以及MN相关曲线时,需要混凝土的本构关系作为输入条件。 1. 代码 这段代码还是比较简单的。不过需要注意的是,我把受拉和受压两种状态统一了…...
)
系统架构设计-架构师之路(八)
软件架构概述 需求分析到软件设计之间的过渡过程就是软件架构。 需求分析人员整理成文档,但是开发人员对业务并不熟悉,这时候中间就需要一个即懂软件又懂业务的人,架构师来把文档整理成系统里的各个开发模块,布置开发任务。 软…...

【SA8295P 源码分析】25 - QNX Ethernet MAC 驱动 之 emac_isr_thread_handler 中断处理函数源码分析
【SA8295P 源码分析】25 - QNX Ethernet MAC 驱动 之 emac_isr_thread_handler 中断处理函数源码分析 一、emac 中断上半部:emac_isr()二、emac 中断下半部:emac_isr_thread_handler()2.1 emac 中断下半部:emac_isr_sw()系列文章汇总见:《【SA8295P 源码分析】00 - 系列文章…...

函数栈帧的创建与销毁
目录 引言 基础知识 内存模型 寄存器的种类与功能 常用的汇编指令 函数栈帧创建与销毁 main()函数栈帧的创建 NO1. NO2. NO3. NO4. NO5. NO6. main()函数栈帧变量的创建 调用Add()函数栈帧的预备工作——传参 NO1. NO2. NO3. Add()函数栈帧的创建 …...

工业安全生产平台在面粉行业的应用分享
一、背景介绍 面粉行业是一个传统的工业行业,安全生产问题一直备受关注。然而,由于生产过程中存在的各种安全隐患和风险,如粉尘爆炸、机械伤害等,使得面粉行业的安全生产形势依然严峻。为了解决这一问题,工业安全生产…...
Gitlab服务部署及应用
目录 Gitlab简介 Gitlab工作原理 Gitlab服务构成 Gitlab环境部署 安装依赖包 启动postfix,并设置开机自启 设置防火墙 下载安装gitlab rpm包 修改配置文件/etc/gitlab/gitlab.rb,生产环境下可以根据需求修改 重新加载配置文件 浏览器登录Gitlab输…...
【nodejs】用Node.js实现简单的壁纸网站爬虫
1. 简介 在这个博客中,我们将学习如何使用Node.js编写一个简单的爬虫来从壁纸网站获取图片并将其下载到本地。我们将使用Axios和Cheerio库来处理HTTP请求和HTML解析。 2. 设置项目 首先,确保你已经安装了Node.js环境。然后,我们将创建一个…...

xlsx xlsx-style file-saver 导出json数据到excel文件并设置标题字体加粗
xlsx:用于处理Excel文件。xlsx-style:用于添加样式到Excel文件中。file-saver:用于将生成的Excel文件保存到用户的计算机上 npm install xlsx xlsx-style file-saver// 导入所需库 const XLSX require(xlsx); const XLSXStyle require(xls…...

Win11游戏高性能模式怎么开
1、点击桌面任务栏上的“开始”图标,在打开的应用中,点击“设置”; 2、“设置”窗口,左侧找到“游戏”选项,在右侧的选项中,找到并点击打开“游戏模式”; 3、打开的“游戏模式”中,找…...
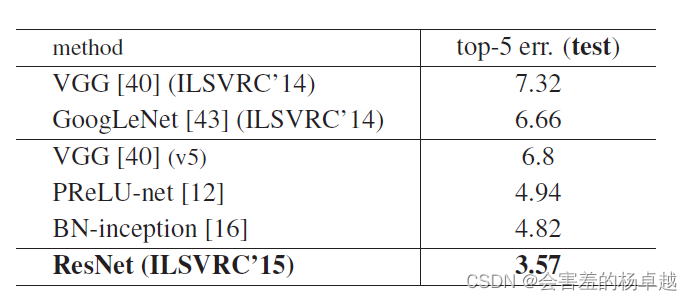
深度学习最强奠基作ResNet《Deep Residual Learning for Image Recognition》论文解读(上篇)
1、摘要 1.1 第一段 作者说深度神经网络是非常难以训练的,我们使用了一个残差学习框架的网络来使得训练非常深的网络比之前容易得很多。 把层作为一个残差学习函数相对于层输入的一个方法,而不是说跟之前一样的学习unreferenced functions 作者提供了…...

第22次CCF计算机软件能力认证
第一题:灰度直方图 解题思路: 哈希表即可 #include<iostream> #include<cstring>using namespace std;const int N 610; int a[N]; int n , m , l;int main() {memset(a , 0 , sizeof a);cin >> n >> m >> l;for(int …...
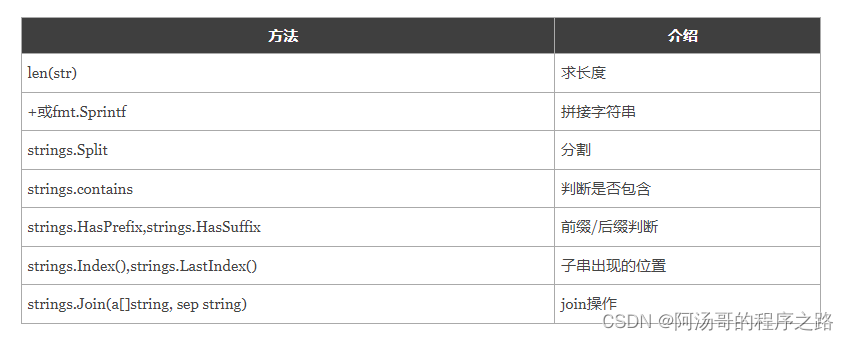
Go语言基础之基本数据类型
Go语言中有丰富的数据类型,除了基本的整型、浮点型、布尔型、字符串外,还有数组、切片、结构体、函数、map、通道(channel)等。Go 语言的基本类型和其他语言大同小异。 基本数据类型 整型 整型分为以下两个大类: 按…...

Linux Tracing Technologies
目录 1. Linux Tracing Technologies 1. Linux Tracing Technologies Linux Tracing TechnologieseBPFXDPDPDK...

iOS自定义下拉刷新控件
自定义下拉刷新控件 概述 用了很多的别人的下拉刷新控件,想写一个玩玩,自定义一个在使用的时候也会比较有意思。使应用更加的灵动一些,毕竟谁不喜欢各种动画恰到好处的应用呢。 使用方式如下: tableview.refreshControl XRef…...
Springboot写单元测试
导入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-test</artifactId><exclusions><exclusion><groupId>org.junit.vintage</groupId><artifactId>junit-vintag…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
