线性代数的学习和整理8： 方阵和行列式相关（草稿-----未完成）
1.4.1 方阵
- 矩阵里，行数=列数的矩阵叫做方阵
- 方阵有很多很好的特殊属性
1.4.2 行列式
- 行列式是方阵的一种特殊运算
- 如果矩阵行数列数相等，那么这个矩阵是方阵。
- 行列数的计算方式和矩阵的不同
- 只有方阵才有行列式
- 行列式其实是，矩阵变化的一个面积变化比率！
1.4.3 矩阵与行列式
- 矩阵是一个数表;
- 行列式是一个n阶的方阵;
- 矩阵不能从整体上被看成一个数;
- 行列式最终可以算出来变成一个数;
- 矩阵的行数和列数可以不同;
- 行列式行数和列数必须相同。
- 矩阵的加法，乘法规律
- 行列式的加法，乘法不同
行列式和计算
3.2 行列式是什么 detA |A|
- 行列式是方阵的，体积变化的系数？
- 一个创造出来的数字 现在：线性变换后测度的值。
- 而如果说行列式为零，那么就是说至少有两个向量在变换之后，共线了。
- 降维了！让人不由自主的想起来二向箔。、
- 行列式为负值代表着翻面了，相对位置发生了调换
行列式的计算
行列式 det
行列式是矩阵的模吗?
怎么在一个晚上搞定线性代数？ - 知乎
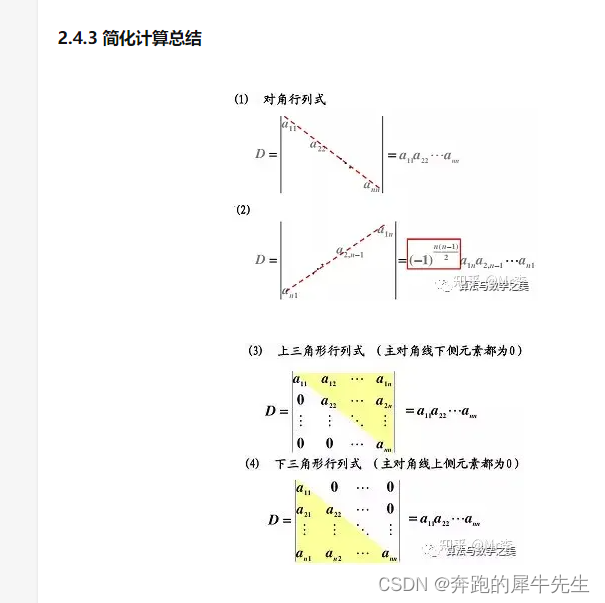
相关文章：
线性代数的学习和整理8： 方阵和行列式相关（草稿-----未完成）
1.4.1 方阵 矩阵里，行数列数的矩阵叫做方阵方阵有很多很好的特殊属性 1.4.2 行列式 行列式是方阵的一种特殊运算如果矩阵行数列数相等，那么这个矩阵是方阵。行列数的计算方式和矩阵的不同只有方阵才有行列式行列式其实是，矩阵变化的一个面…...
Ubuntu vi 左下角没有提示
1 打开终端，输入以下命令 sudo gedit /etc/vim/vimrc.tiny 2 进入文件后，修改 set compatible 为set nocompatible，如下所示： " Vim configuration file, in effect when invoked as "vi". The aim of this "…...
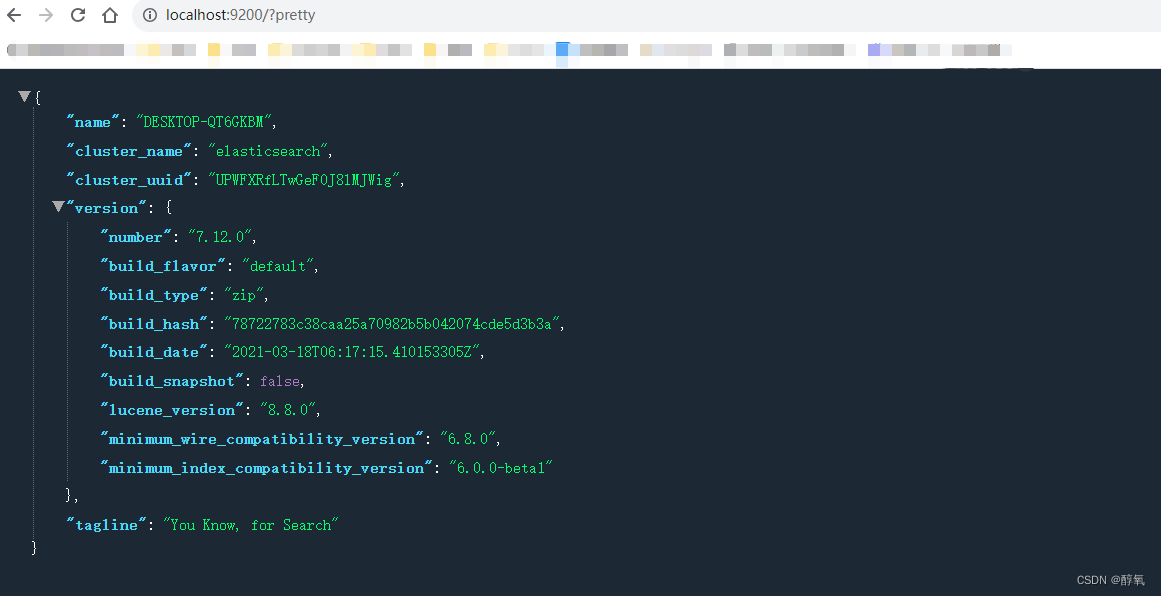
Windows安装 Elasticsearch 教程
下载地址 Past Releases of Elastic Stack Software | Elastic 解压 解压完的样子 进入BIN目录 D:\Develop\elasticsearch\elasticsearch-7.12.0\bin 按住shift 鼠标右键 打开 powershell 窗口 查看ES版本 .\elasticsearch.bat --version 出现问题了 警告：不赞成…...
Dubbo 融合 Nacos 成为注册中心
快速上手 Dubbo 融合 Nacos 成为注册中心的操作步骤非常简单，大致步骤可分为“增加 Maven 依赖”以及“配置注册中心“。 增加 Maven 依赖 只需要依赖Dubbo客户端即可，关于推荐的使用版本，请参考Dubbo官方文档或者咨询Dubbo开发人员&#…...
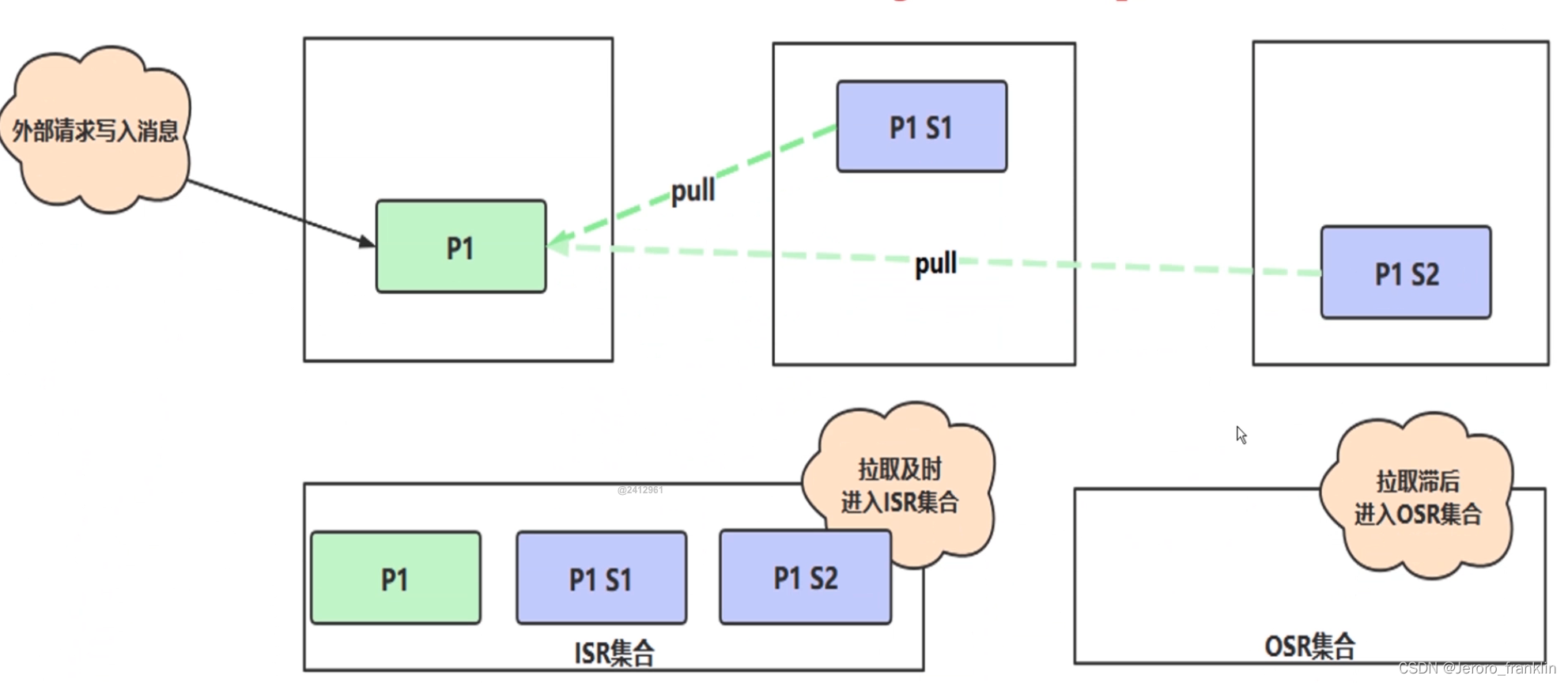
kafka--kafka基础概念-ISR详解
kafka基础概念-ISR详解 主要是讲 主 往 从同步中的问题 当绿色P1接收到写入的数据，要同步到紫色的P1S1和P1S2 如何保证一致性呢？ 使用In Sync Replicas 也就是ISR概念 为什么不一致的？ 因为P1S1同步数据 可能花费 50ms P1S2可能花费60ms…...
《Kubernetes部署篇：Ubuntu20.04基于外部etcd+部署kubernetes1.24.16集群(多主多从）》
一、架构图 如下图所示： 二、环境信息 1、部署规划 主机名K8S版本系统版本内核版本IP地址备注k8s-master-631.24.16Ubuntu 20.04.5 LTS5.15.0-69-generic192.168.1.63master节点 + etcd节点k8s-master-641.24.16Ubuntu 20.04.5 LTS5.15.0-69-generic192.168.1.64master节点 + …...
音频解码及如何在Java实现
本人并不干这个，但是被迫下水了解了一下这个，稍微做了一下整理。再就是感觉现在网上以及ChatGPT在这方面给出的答案太水了，在此开辟一篇。无意放出代码，这里只介绍一些可能重要的点。 本来以为有了ChatGPT写这些就没有必要了&…...
Webshell 及检测绕过
webshell 概念 web指的是在web服务器上，而shell是用脚本语言编写的脚本程序，WebShell是一种用来进行网站和服务器管理的脚本程序,webshell一般是被网站管理员用于网站管理、服务器管理等等一些用途，但是由于webshell的功能比较强大࿰…...
Ubuntu22.4系统mongodb数据库安装
Ubuntu22.4系统mongodb数据库安装 1、打开终端并运行以下命令，以导入 MongoDB GPG 密钥： wget -qO - https://www.mongodb.org/static/pgp/server-5.0.asc | sudo apt-key add -2、添加 MongoDB 仓库到你的系统。根据你的 Ubuntu 版本，选择…...
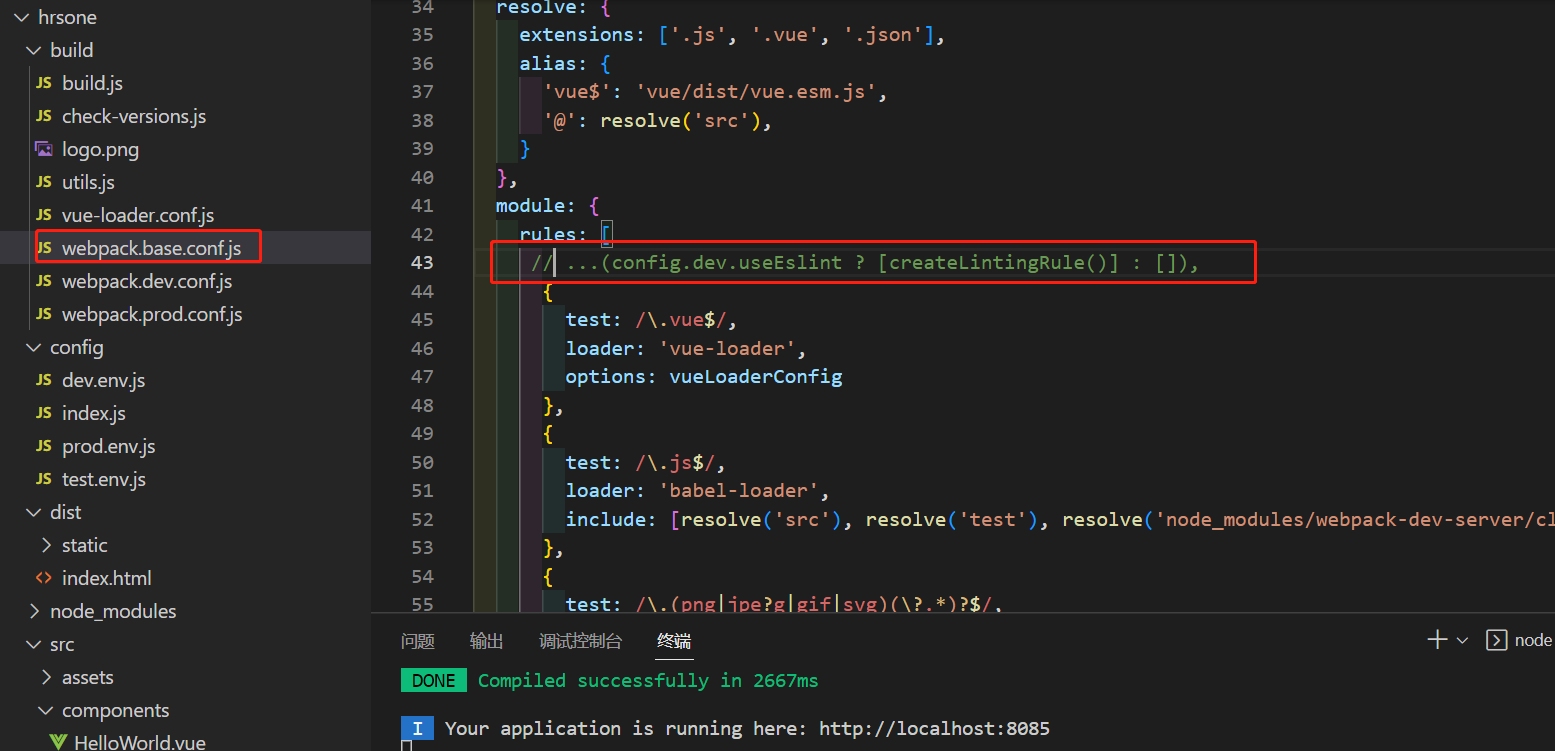
Vue初识别--环境搭建--前置配置过程
问题一： 在浏览器上的扩展程序上添加了vue-devtools后不生效： 解决方式：打开刚加入的扩展工具Vue.js devtools的允许访问文件地址设置 问题二：Vue新建一个项目 创建一个空文件夹hrsone，然后在VSCode中打开这个空文件夹…...
数据在内存中的储存·大小端（文字+画图详解）（c语言·超详细入门必看）
前言：Hello，大家好，我是心跳sy😘，本节我们介绍c语言的两种基本的内置数据类型：数值类型和字符类型在内存中的储存方法，并对大小端进行详细介绍（附两种大小端判断方法）&am…...
Word怎么转换成PDF文档？多个Word转换成PDF步骤分享
word文档是一种非常好用的文件格式，可以帮助用户们很好的保存图片和文字内容，不过并不是只有word这一种文档类文件格式，还有一种pdf文档也深受用户们的欢迎，在工作或者学习过程中这两种文档是可以互相转换格式的，那么W…...
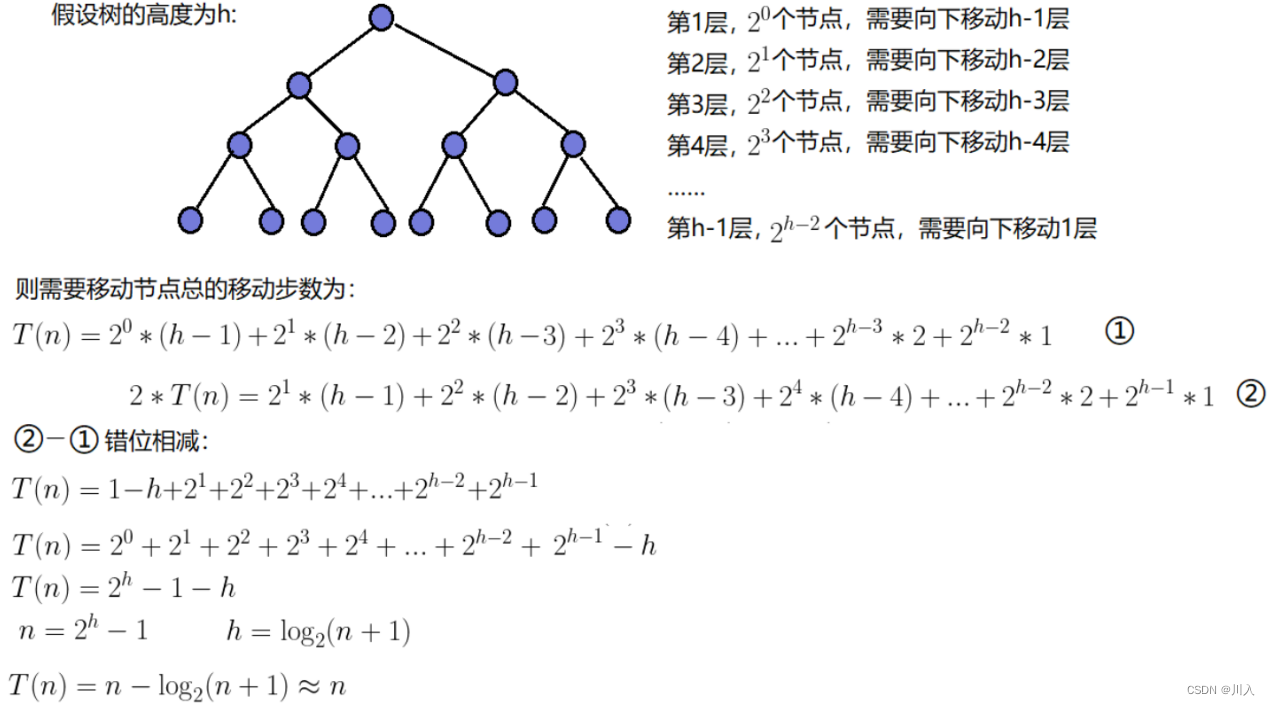
【C++习题集】-- 堆
（用于复习） 目录 树概念及结构 名词概念 二叉树概念及结构 特殊的二叉树 满二叉树 完全二叉树 运算性质 二叉树存储结构 顺序存储 链式存储 堆 - 顺序存储 堆的性质 堆的实现 堆的应用 堆排序 直接建堆法 树概念及结构 概念：…...
vue + vue-office 实现多种文件(docx、excel、pdf)的预览
支持多种文件( docx、excel、pdf)预览的vue组件库，支持vue2/3。也支持非Vue框架的预览。 github: 《仓库地址》 演 示： 《演示效果》 功能特色 一站式：提供docx、pdf、excel多种文档的在线预览方案，有它就够了简单：…...
30.Netty源码服务端启动主要流程
highlight: arduino-light 服务端启动主要流程 •创建 selector •创建 server socket channel •初始化 server socket channel •给 server socket channel 从 boss group 中选择一个 NioEventLoop •将 server socket channel 注册到选择的 NioEventLoop 的 selector •…...
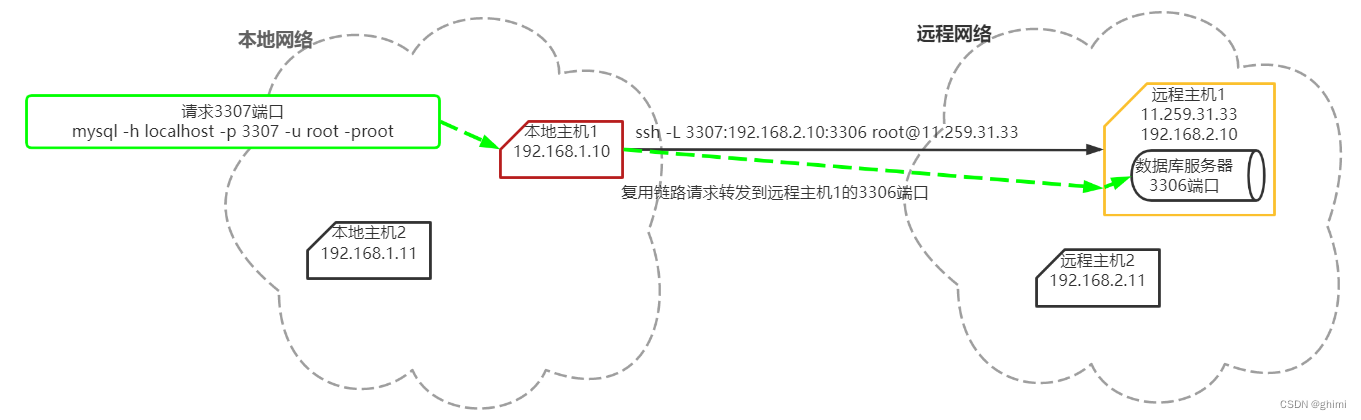
ssh端口转发
在本地客户端操作： ssh远程连接一段时间会失效的问题 vim /etc/ssh_config或vim /etc/ssh/ssh_config 在末尾添加ServerAliveInterval 30，意思是30s会发送一次向服务器连接的请求，以保持会话始终在线 验证: 放一段时间不操作，…...
独立站SEO是什么意思？自主网站SEO的含义？
什么是独立站SEO优化？自建站搜索引擎优化是指什么？ 独立站SEO，作为网络营销的重要一环，正在逐渐引起人们的关注。在当今数字化时代，独立站已经成为许多企业、个人宣传推广的首选平台之一。那么，究竟什么是…...
Android JNI系列详解之NDK和JNI介绍
一、前提 针对自己在Android JNI和NDK这块技术的空白知识点，进行这个JNI系列的学习，记录这一阶段的学习。学习的主要步骤：从概念原理解析--->边学边实战--->从易到难，循序渐进。（学习这一阶段的前提：需要有Android开发基础） 学完JNI-NDK开发系列，达到的目的有：…...
LeetCode //C - 20. Valid Parentheses
20. Valid Parentheses Given a string s containing just the characters ‘(’, ‘)’, ‘{’, ‘}’, ‘[’ and ‘]’, determine if the input string is valid. An input string is valid if: Open brackets must be closed by the same type of brackets.Open bracke…...
浅析Java设计模式之四策略模式
title: 浅析Java设计模式之四策略模式 date: 2018-12-29 17:26:17 categories: 设计模式 description: 浅析Java设计模式之四策略模式 1. 目录 1. 目录2. 概念 2.1. 应用场景2.2. 优缺点 2.2.1. 优点2.2.2. 缺点 3. 模式结构4. 样例 4.1. 定义策略4.2. 定义具体策略4.3. 定义…...
浏览器访问 AWS ECS 上部署的 Docker 容器（监听 80 端口）
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义（Task Definition&…...
conda相比python好处
Conda 作为 Python 的环境和包管理工具，相比原生 Python 生态（如 pip 虚拟环境）有许多独特优势，尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处： 一、一站式环境管理：…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装（Encapsulation） 定义：将数据（属性）和操作数据的方法绑定在一起，通过访问控制符（private、protected、public）隐藏内部实现细节。示例： public …...
MySQL 隔离级别：脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别，用于控制事务之间的并发访问以及数据的可见性，不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式，具体如下： 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交（READ UNCOMMITTED）允许出现允许…...
Opencv中的addweighted函数
一.addweighted函数作用 addweighted（）是OpenCV库中用于图像处理的函数，主要功能是将两个输入图像（尺寸和类型相同）按照指定的权重进行加权叠加（图像融合），并添加一个标量值&#x…...
el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...
生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端（Windows 使用 Git Bash，Mac/Linux 使用 Terminal）执行命令： ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明： -t rsa&#x…...
Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库，例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体，比如 SnowballFight、Huggy the Do…...
多模态大语言模型arxiv论文略读（108）
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题：CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者：Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...