【C++习题集】-- 堆
(用于复习)
目录
树概念及结构
名词概念
二叉树概念及结构
特殊的二叉树
满二叉树
完全二叉树
运算性质
二叉树存储结构
顺序存储
链式存储
堆 - 顺序存储
堆的性质
堆的实现
堆的应用
堆排序
直接建堆法
树概念及结构
概念:非线性的数据结构(形成的倒挂似树的结构 - 根朝上,叶朝下,子树之间不能有交集)。

名词概念
- 节点的度:一个节点含有的子树的个数称为该节点的度。
- 叶节点或终端节点:度为0的节点称为叶节点。
- 非终端节点或分支节点:度不为0的节点。
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点。
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点。
- 兄弟节点:具有相同父节点的节点互称为兄弟节点。
- 树的度:一棵树中,最大的节点的度称为树的度。
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推。
- 树的高度或深度:树中节点的最大层次。
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟。
- 节点的祖先:从根到该节点所经分支上的所有节点。
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>0)棵互不相交的树的集合称为森林。
二叉树概念及结构
由一个根节点加上两棵别称为左子树和右子树的二叉树组成 - 子树可为空。

- 不存在度大于2的结点。
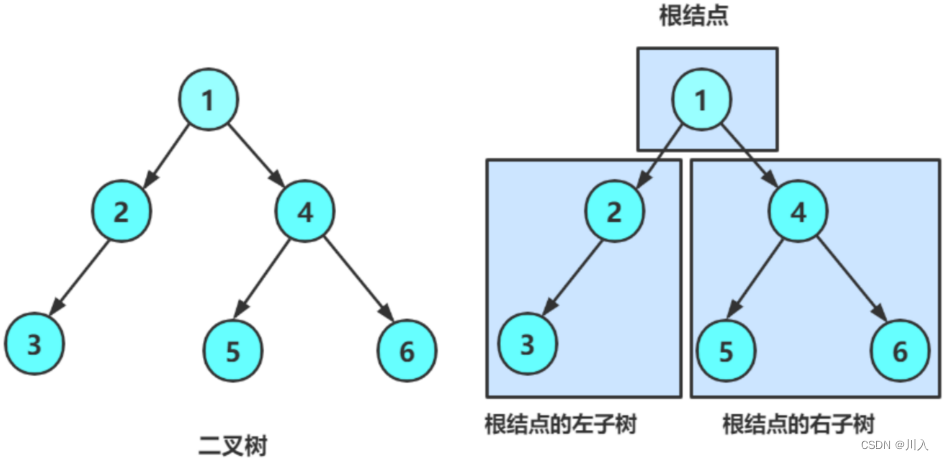
特殊的二叉树
满二叉树
每一个层的结点数都达到最大值,则结点总数:2^k - 1(K层数)。

完全二叉树
特殊的完全二叉树 - 最后一层不满,但是是左到右是连续的。
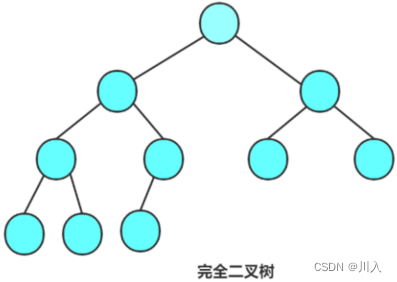
(满二叉树是特殊的完全二叉树)
运算性质
- 根节点的层数为1,则第i层上最多有2^(i - 1)个结点
- 根节点的层数为1,则深度h的最大结点数是2^h - 1
- 根节点的层数为1,n个结点的满二叉树的深度h = log2(n + 1)
- 如果度为0其叶结点个数为n,度为2的分支结点个数为m,则有:n = m + 1
- n个结点的完全二叉树,以数组顺序对所有节点开始编号:
- 若i>0,i位置节点的双亲序号:(i - 1) / 2
- 若2i + 1 < n,左孩子序号:2i + 1,2i + 1 >= n否则无左孩子
- 若2i + 2 < n,右孩子序号:2i + 2,2i + 2 >= n否则无右孩子
一个具有767个节点的完全二叉树,其叶子节点个数为()
A、383B、384C、385D、386------------------------------------------正确答案:B------------------------------------------解析:不要只想最后一层,倒数第二层也是会有叶子节点的。首先以:
可以推算出是第1 ~ 9层为满二叉树,对应节点数:511。可以知道最后一层一定为叶子节点:256个。
然后根据完全二叉树是最后一层不满,但是是左到右是连续的,于是256 / 2 = 128,所以倒数第二层有128个是最后一层的父节点。
再根据:
可知倒数第二层有256个节点,于是叶子节点:256 + 256 - 128 = 384。
二叉树存储结构
顺序存储
用数组来存储,适合表示完全二叉树。
- 物理上:数组
- 逻辑上:二叉树

链式存储
用链表来表示一棵二叉树。
- 二叉链:数据域和左右指针域
- 三叉链:数据域和左右上指针域

堆 - 顺序存储
堆是一种特殊的完全二叉树,只不过父亲与儿子节点间有关系。顺序存储的完全二叉树典型的就是堆。(普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储)
堆的性质
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 小堆:父亲位,比孩子位,要小
- 大堆:父亲位,比孩子位,要大
- 堆总是一棵完全二叉树

堆的实现
#include <iostream>
#include <cassert>namespace qcr_heap
{typedef int HeapType;struct Heap{int64_t _capacity; // 动态开辟可用大小int64_t _size; // 实际数据占用大小HeapType *_array; // 动态开辟一维数组};/********** 初始化堆*********/void HeapInit(Heap *heap){assert(heap);heap->_capacity = 0;heap->_size = 0;heap->_array = 0;}/********** 销毁堆*********/void HeapDestory(Heap *heap){assert(heap);heap->_capacity = 0;heap->_size = 0;free(heap->_array);heap->_array = nullptr;}/********** 小根堆*********/bool less(HeapType element_1, HeapType element_2){return element_1 < element_2;}/********** 大根堆*********/bool greater(HeapType element_1, HeapType element_2){return element_1 > element_2;}/********** 交换数据*********/void swap(HeapType *element_1, HeapType *element_2){HeapType tmp = *element_1;*element_1 = *element_2;*element_2 = tmp;}/****************************** 向上调整* heap: 输入型参数,堆地址* child: 输入型参数,排序的插入节点* Func: 输入型参数,大小堆*****************************/void AdjustUp(Heap *heap, int64_t child, bool (*Func)(HeapType, HeapType)){assert(heap);int64_t parent = (child - 1) / 2;while (child > 0){if (Func(heap->_array[child], heap->_array[parent])){swap(&(heap->_array[child]), &(heap->_array[parent]));child = parent;parent = (child - 1) / 2;}elsebreak;}}/****************************** 向下调整* heap: 输入型参数,堆地址* root: 输入型参数,排序的根节点* Func: 输入型参数,大小堆*****************************/void AdjustDown(Heap *heap, int64_t root, bool (*Func)(HeapType, HeapType)){assert(heap);int64_t parent = root;int64_t child = parent * 2 + 1;while (child < heap->_size){if (child + 1 < heap->_size && Func(heap->_array[child + 1], heap->_array[child])){child++;}if (Func(heap->_array[child], heap->_array[parent])){swap(&(heap->_array[child]), &(heap->_array[parent]));parent = child;child = parent * 2 + 1;}else{break; // 符合堆就成立了,就没必要进行交换了。}}}/****************************** 存入数据* heap: 输入型参数,堆地址* data: 输入型参数,插入的数据* Func: 输入型参数,大小堆*****************************/void HeapPush(Heap *heap, HeapType data, bool (*Func)(HeapType, HeapType)){assert(heap);if (heap->_capacity == heap->_size){int64_t newcapacity = heap->_capacity == 0 ? 5 : heap->_capacity * 2;HeapType * tmp = (HeapType *)realloc(heap->_array, heap->_capacity*sizeof(HeapType);if (tmp == nullptr){printf("Capacuty Get Error!\n");exit(-1);}heap->_array = tmp;heap->_capacity = newcapacity;}heap->_array[heap->_size] = data;AdjustUp(heap, heap->_size, Func);(heap->_size)++;}/****************************** 按顺序全部输出* heap: 输入型参数,堆地址*****************************/void HeapPrint(Heap *heap){assert(heap);for (uint64_t i = 0; i < heap->_size; i++){std::cout << heap->_array[i] << " ";}std::cout << '\n';}/****************************** 首元素* heap: 输入型参数,堆地址*****************************/HeapType HeapTop(Heap *heap){assert(heap);assert(heap->_size > 0);return heap->_array[0];}/****************************** 判空* heap: 输入型参数,堆地址*****************************/bool HeapEmpty(Heap *heap){assert(heap);return heap->_size == 0;}/****************************** 有效数据个数* heap: 输入型参数,堆地址*****************************/int HeapSize(Heap *heap){assert(heap);return heap->_size;}/****************************** 判空* heap: 输入型参数,堆地址* Func: 输入型参数,大小堆*****************************/void HeapPop(Heap *heap, bool (*Func)(HeapType, HeapType)){assert(heap);assert(heap->_size > 0);heap->_array[0] = heap->_array[heap->_size - 1];(heap->_size)--;AdjustDown(heap, 0, Func);}
}已知小根堆为8,15,10,21,34,16,12,删除关键字 8 之后需重建堆,在此过程中,关键字之间的比较次数是()A、1B、2C、3D、4------------------------------------------正确答案:B------------------------------------------解析:首先我们需要知道,删除对应的调整算法是向下调整,所以其实在比较中有一个很重要的一项就是左右节点的比较,于是此处本质上的比较是需要在加上一次左右节点的比较。
堆的应用
堆排序
利用堆删除思想来进行排序。
TOP-K问题
1. 用数据集合中前K个元素来建堆
- 前k个最大的元素,则建小堆
- 前k个最小的元素,则建大堆
面试题 17.14. 最小K个数 - 力扣(LeetCode)
class Solution
{
public:// 向上建堆void adjustUp(vector<int> &nums, int child){int parent = (child - 1) / 2;while (child > 0){if (nums[child] > nums[parent]){swap(nums[child], nums[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}// 向下建堆void adjustDown(vector<int> &nums, int parent){int child = parent * 2 + 1;while (child < nums.size()){if (child + 1 < nums.size() && nums[child + 1] > nums[child]){child++;}if (nums[child] > nums[parent]){swap(nums[child], nums[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}// 堆排序的TOP-k问题vector<int> smallestK(vector<int> &arr, int k){vector<int> nums;nums.reserve(k);// 前K个元素来建堆for (int i = 0; i < k; i++){nums.push_back(arr[i]);adjustUp(nums, nums.size() - 1);}// 对比堆顶元素if (k != 0){for (int i = k; i < arr.size(); i++){if (arr[i] < nums[0]){nums[0] = arr[i];adjustDown(nums, 0);}}}return nums;}
};并不是最优的,并且还实现了两个堆算法,编码效率过低。
直接建堆法
原本利用向上建堆的方式,是并不够完美的,建堆的时间复杂度为O(N)。
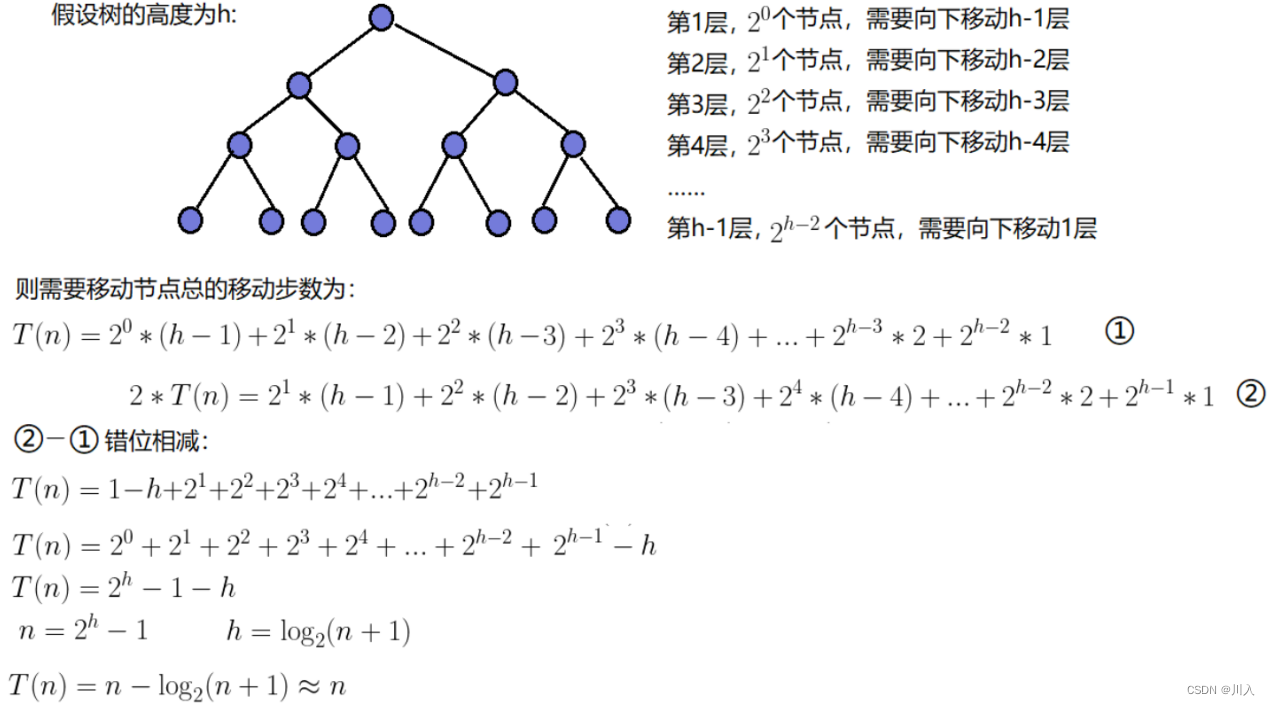
而直接建堆法时间复杂度O(logn),其根本是利用向下建堆实现。
for (int i = (size - 1 - 1) / 2; i >= 0; i--)
{ADjustDown(nums, i);
}class Solution
{
public:// 向下建堆void adjustDown(vector<int> &nums, int parent){int child = parent * 2 + 1;while (child < nums.size()){if (child + 1 < nums.size() && nums[child + 1] > nums[child]){child++;}if (nums[child] > nums[parent]){swap(nums[child], nums[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}// 堆排序的TOP-k问题vector<int> smallestK(vector<int> &arr, int k){vector<int> nums;nums.reserve(k);// 前K个元素来建堆for (int i = 0; i < k; i++){nums.push_back(arr[i]);}for(int i = (k - 1 - 1) / 2; i >= 0; i--){adjustDown(nums, i);}// 对比堆顶元素if (k != 0){for (int i = k; i < arr.size(); i++){if (arr[i] < nums[0]){nums[0] = arr[i];adjustDown(nums, 0);}}}return nums;}
};相关文章:

【C++习题集】-- 堆
(用于复习) 目录 树概念及结构 名词概念 二叉树概念及结构 特殊的二叉树 满二叉树 完全二叉树 运算性质 二叉树存储结构 顺序存储 链式存储 堆 - 顺序存储 堆的性质 堆的实现 堆的应用 堆排序 直接建堆法 树概念及结构 概念:…...

vue + vue-office 实现多种文件(docx、excel、pdf)的预览
支持多种文件( docx、excel、pdf)预览的vue组件库,支持vue2/3。也支持非Vue框架的预览。 github: 《仓库地址》 演 示: 《演示效果》 功能特色 一站式:提供docx、pdf、excel多种文档的在线预览方案,有它就够了简单:…...

30.Netty源码服务端启动主要流程
highlight: arduino-light 服务端启动主要流程 •创建 selector •创建 server socket channel •初始化 server socket channel •给 server socket channel 从 boss group 中选择一个 NioEventLoop •将 server socket channel 注册到选择的 NioEventLoop 的 selector •…...
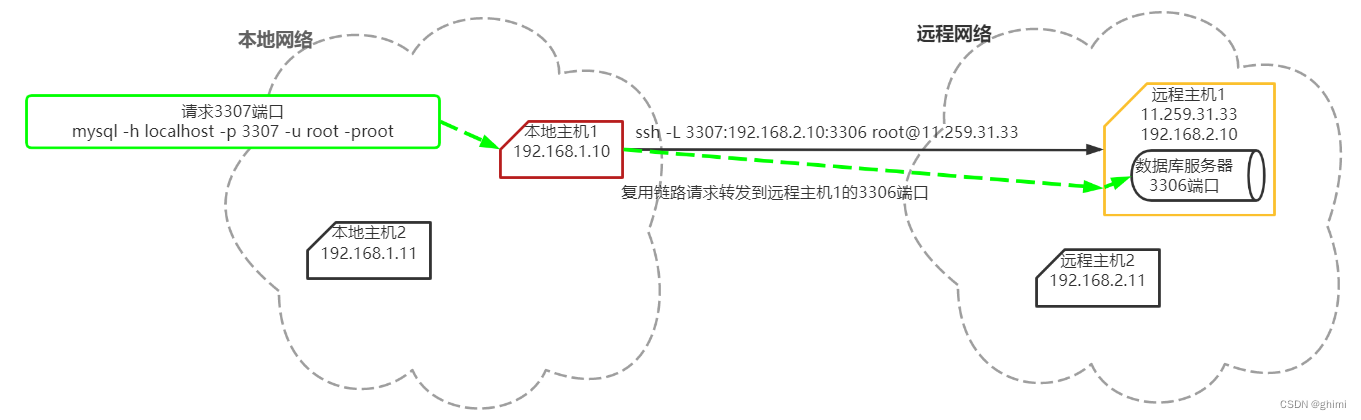
ssh端口转发
在本地客户端操作: ssh远程连接一段时间会失效的问题 vim /etc/ssh_config或vim /etc/ssh/ssh_config 在末尾添加ServerAliveInterval 30,意思是30s会发送一次向服务器连接的请求,以保持会话始终在线 验证: 放一段时间不操作,…...
独立站SEO是什么意思?自主网站SEO的含义?
什么是独立站SEO优化?自建站搜索引擎优化是指什么? 独立站SEO,作为网络营销的重要一环,正在逐渐引起人们的关注。在当今数字化时代,独立站已经成为许多企业、个人宣传推广的首选平台之一。那么,究竟什么是…...

Android JNI系列详解之NDK和JNI介绍
一、前提 针对自己在Android JNI和NDK这块技术的空白知识点,进行这个JNI系列的学习,记录这一阶段的学习。学习的主要步骤:从概念原理解析--->边学边实战--->从易到难,循序渐进。(学习这一阶段的前提:需要有Android开发基础) 学完JNI-NDK开发系列,达到的目的有:…...

LeetCode //C - 20. Valid Parentheses
20. Valid Parentheses Given a string s containing just the characters ‘(’, ‘)’, ‘{’, ‘}’, ‘[’ and ‘]’, determine if the input string is valid. An input string is valid if: Open brackets must be closed by the same type of brackets.Open bracke…...
浅析Java设计模式之四策略模式
title: 浅析Java设计模式之四策略模式 date: 2018-12-29 17:26:17 categories: 设计模式 description: 浅析Java设计模式之四策略模式 1. 目录 1. 目录2. 概念 2.1. 应用场景2.2. 优缺点 2.2.1. 优点2.2.2. 缺点 3. 模式结构4. 样例 4.1. 定义策略4.2. 定义具体策略4.3. 定义…...
基于Spring Boot的餐厅订餐网站的设计与实现(Java+spring boot+MySQL)
获取源码或者论文请私信博主 演示视频: 基于Spring Boot的餐厅订餐网站的设计与实现(Javaspring bootMySQL) 使用技术: 前端:html css javascript jQuery ajax thymeleaf 微信小程序 后端:Java springbo…...
评估指标代码实现)
【图像分割】理论篇(1)评估指标代码实现
图像分割是计算机视觉中的重要任务,用于将图像中的不同区域分割成具有语义意义的区域。以下是几种常用的图像分割评价指标以及它们的代码实现示例(使用Python和常见的计算机视觉库): 1. IoU (Intersection over Union) 与目标检…...

Git checkout 某个版本到指定文件夹下
文章目录 场景说明方案一:git archive 最简单省事方案二:git show 最灵活, 但文件较多时麻烦方案三:git --work-tree 有bug 场景说明 我不想checkout到覆盖本地工作区的文件, 而是想把该版本checkout到另外一个文件夹下ÿ…...
)
Java多态详解(2)
向上转型和向下转型 向上转型 定义:实际就是创建一个子类对象,将其当作父类对象来使用。 语法格式:父类类型 对象名 new 子类类型() Animal animal new Cat("元宝", 2); animal是父类类型,但是可以引用子…...
Camtasia导入srt字幕乱码
我们在使用camtasia制作视频项目时,有时为了用户体验需要导入srt格式的字幕文件,在操作无误的情况下,一顿操作猛如虎之后字幕顺利的导入到软件中了,但字幕却出现了乱码的现象。如下图所示: 如何解决srt乱码问题呢&…...
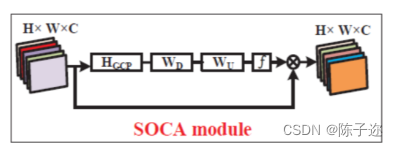
YOLOv5、YOLOv8改进:SOCA注意力机制
目录 简介 2.YOLOv5使用SOCA注意力机制 2.1增加以下SOCA.yaml文件 2.2common.py配置 2.3yolo.py配置 简介 注意力机制(Attention Mechanism)源于对人类视觉的研究。在认知科学中,由于信息处理的瓶颈,人类会选择性地关注所有…...

机器人的运动范围
声明 该系列文章仅仅展示个人的解题思路和分析过程,并非一定是优质题解,重要的是通过分析和解决问题能让我们逐渐熟练和成长,从新手到大佬离不开一个磨练的过程,加油! 原题链接 机器人的运动范围https://leetcode.c…...
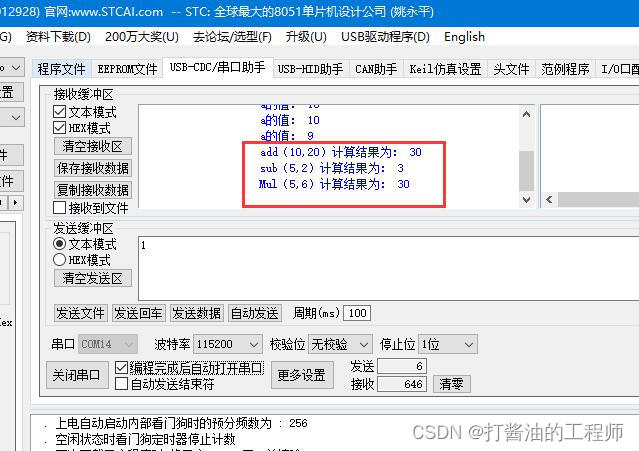
学习笔记|基于Delay实现的LED闪烁|模块化编程|SOS求救灯光|STC32G单片机视频开发教程(冲哥)|第六集(下):实现LED闪烁
文章目录 2 函数的使用1.函数定义(需要带类型)2.函数声明(需要带类型)3.函数调用 3 新建文件,使用模块化编程新建xxx.c和xxx.h文件xxx.h格式:调用头文件验证代码调用:完整的文件结构如下&#x…...
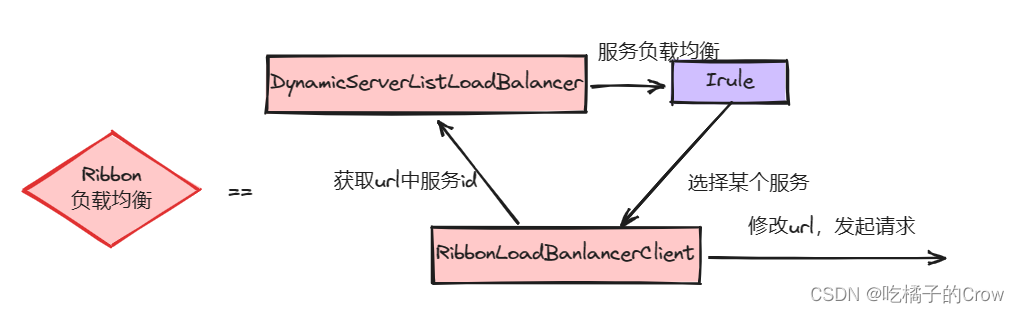
微服务-Ribbon(负载均衡)
负载均衡的面对多个相同的服务的时候,我们选择一定的策略去选择一个服务进行 负载均衡流程 Ribbon结构组成 负载均衡策略 RoundRobinRule:简单的轮询服务列表来选择服务器AvailabilityFilteringRule 对两种情况服务器进行忽略: 1.在默认情…...
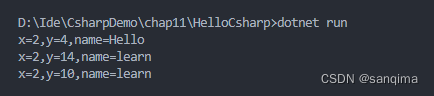
解决C#报“MSB3088 未能读取状态文件*.csprojAssemblyReference.cache“问题
今天在使用vscode软件C#插件,编译.cs文件时,发现如下warning: 图(1) C#报cache没有更新 出现该warning的原因:当前.cs文件修改了,但是其缓存文件*.csprojAssemblyReference.cache没有更新,需要重新清理一下工程&#x…...
GeoScene Pro在地图制图当中的应用
任何地理信息系统建设过程中,背景地图的展示效果对整个系统功能的实现没有直接影响;但是地图的好看与否,会间接的决定着整个项目的高度。 一幅精美的地图不仅能令人赏心悦目、眼前一亮,更能将人吸引到你的系统中,更愿意…...

国标混凝土结构设计规范的混凝土本构关系——基于python代码生成
文章目录 0. 背景1. 代码2. 结果测试 0. 背景 最近在梳理混凝土塔筒的计算指南,在求解弯矩曲率关系以及MN相关曲线时,需要混凝土的本构关系作为输入条件。 1. 代码 这段代码还是比较简单的。不过需要注意的是,我把受拉和受压两种状态统一了…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

