【管理运筹学】第 5 章 | 整数规划 (2,割平面法及 0-1 变量的特性)
文章目录
- 引言
- 三、割平面法
- 四、0-1 型整数规划
- 4.1 0-1 变量的特性
- 4.1.1 投资问题
- 4.1.2 约束条件满足个数问题
- 写在最后
引言
前文我们介绍了整数规划的一种求解方法——分支定界法,可以求解纯整数和混合整数规划问题。现在我们来学习另一种整数规划求解方法——割平面法。
接着,我们还会涉及到 0-1 整数规划的一些内容,是整数规划的一种特殊情形。
三、割平面法
割平面法是受整数规划几何解释的启发而形成的,根据前文的讨论,整数规划的最优解一定是在线性规划松弛问题的最优解附近。

那么,是否可以增加一些附加的约束,将松弛问题最优解附近不含整数解的可行域的多余部分分割来对最优解进行搜索呢?下面我们通过例子来感受割平面法的工作原理。
用割平面法求解下列整数规划问题。

解: 用单纯形法求解线性规划松弛问题,得到的最优单纯形表如下:
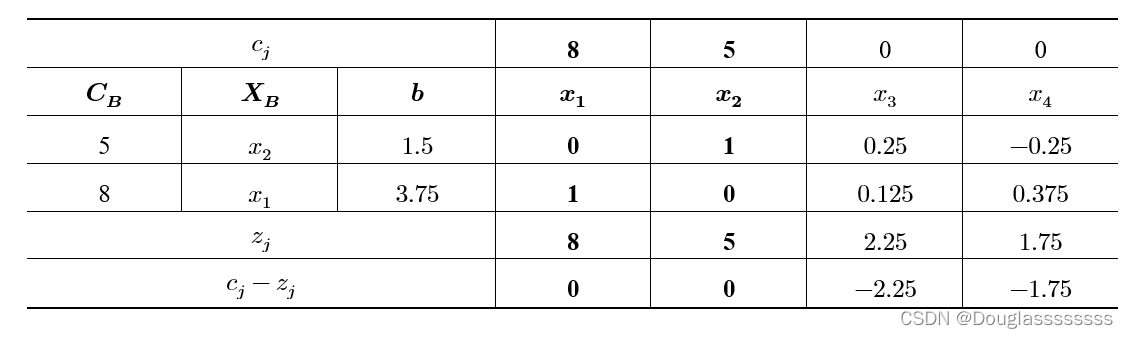
其松弛问题最优解为 ( x 1 = 3.75 , x 2 = 1.5 , z = 37.5 ) (x_1=3.75,x_2=1.5,z=37.5) (x1=3.75,x2=1.5,z=37.5) 。两个基变量均不满足整数要求。割平面通过加入割约束,来割除多余部分。加入割约束的方法为:
从非整数基变量对应的约束条件中任选一个。假定选取第二个,即 x 1 x_1 x1 在最优单纯性表中对应约束。该约束可表示为: x 1 + 0.125 x 3 + 0.375 x 4 = 3.75 x_1+0.125x_3+0.375x_4=3.75 x1+0.125x3+0.375x4=3.75 将上式所有非整数系数写成一个整数和纯正小数之和,即 x 1 + ( 0 + 0.125 ) x 3 + ( 0 + 0.375 x 4 ) = 3 + 0.75 x_1+(0+0.125)x_3+(0+0.375x_4)=3+0.75 x1+(0+0.125)x3+(0+0.375x4)=3+0.75 接着将所有整数项移到等式右边,小数项移到等式左边,可得: x 1 − 3 = 0.75 − 0.125 x 3 − 0.375 x 4 x_1-3=0.75-0.125x_3-0.375x_4 x1−3=0.75−0.125x3−0.375x4 上式,等式左端为整数,则右端也必须为整数。右端 x 3 , x 4 x_3,x_4 x3,x4 均为非负整数,要求等式右端为整数的话,则等式右端要小于等于 0 ,即 0.75 − 0.125 x 3 − 0.375 x 4 ≤ 0 0.75-0.125x_3-0.375x_4 \leq 0 0.75−0.125x3−0.375x4≤0 整理即 − x 3 − 3 x 4 ≤ − 6 -x_3-3x_4 \leq -6 −x3−3x4≤−6 。将其化为等式,添加到之前的最优单纯形表中,利用对偶单纯形法继续求解,得到最优整数解为 ( x 1 = 2 , x 2 = 3 , z = 34 ) (x_1=2,x_2=3,z=34) (x1=2,x2=3,z=34) 。
新加入的割约束方程不会割除任何整数解,即原问题的所有整数解都满足新增加的割约束。
四、0-1 型整数规划
0-1 型整数规划的变量 x i x_i xi 仅取值 0 或 1 。称 x i x_i xi 为 0-1 变量或二进制变量。这一条件可以用以下约束来代替: x i ≤ 1 , x i ≥ 0 , 整数 x_i \leq 1,x_i \geq0,整数 xi≤1,xi≥0,整数
4.1 0-1 变量的特性
面对实际问题中比如逻辑条件或顺序要求等特殊的约束条件,引入 0-1 变量可以非常巧妙地加以表示。下面讨论几个问题,大家就能感受到了。
4.1.1 投资问题
某投资公司可用于投资的资金总额为 b b b ,有若干个项目可供选择投资,假设其中第 j j j 个项目每年可获取利润 c j c_j cj ,所需要的资金是 a j a_j aj ,问如何建立模型来选定最佳组合的投资项目,以取得最佳利润。
这个问题是比较棘手的,但如果引入一个 0-1 变量,建模就变得较为直观和轻松了。因为每一种项目只有两种状态,因此,令 x j = 1 x_j=1 xj=1 表示投资了第 j j j 个项目, x j = 0 x_j=0 xj=0 表示不投资该项目。可列出如下规划模型:

0-1 变量还可以帮助我们满足现实投资问题中特殊的要求,如下列举了一些例子。
排斥需求—— 某几个项目(假设为第 1,4,5 个项目)中至多只能选一个,约束方程可以表示为 x 1 + x 4 + x 5 ≤ 1. x_1+x_4+x_5 \leq 1. x1+x4+x5≤1.
优先级需求—— 选择了第 2 个项目时,才能考虑选择第 3 个项目,约束可表示为 x 3 ≤ x 2 . x_3 \leq x_2. x3≤x2. 同时选择了第 1,2 个项目时,才能考虑选择第 3 个项目,则约束方程可表示为 2 x 3 ≤ x 1 + x 2 . 2x_3 \leq x_1+x_2. 2x3≤x1+x2.
不可缺需求—— 第 3,4 个项目至少要有一个选择投资,则约束方程可表示为 x 3 + x 4 ≥ 1. x_3+x_4 \geq 1. x3+x4≥1.
4.1.2 约束条件满足个数问题
用下式表示 p p p 个约束条件方程: ∑ j = 1 n a i j x j ≤ b i , i = 1 , 2 , … , p \sum_{j=1}^na_{ij}x_j \leq b_i,i=1,2,\dots,p j=1∑naijxj≤bi,i=1,2,…,p 设 y i y_i yi 为 0-1 变量,如果让第 i i i 个约束条件起作用,则 y i y_i yi 取 1 ,否则取 0 ,即有下式: ∑ j = 1 n a i j x j ≤ b i + ( 1 − y i ) M , i = 1 , 2 , … , p \sum_{j=1}^na_{ij}x_j \leq b_i+(1-y_i)M,i=1,2,\dots,p j=1∑naijxj≤bi+(1−yi)M,i=1,2,…,p 其中, M M M 是很大的整数。此时如何 y i y_i yi 为 0 ,则不等式右端为 b i + M b_i+M bi+M ,显然对任意 x x x 均满足,因此不具有约束力。
若要求必须满足 k k k 个约束条件,可添加条件 ∑ y i = k \sum y_i=k ∑yi=k 。要求至少满足 k k k 个约束条件,可添加条件 ∑ y i ≥ k . \sum y_i \geq k. ∑yi≥k.
写在最后
后文将介绍 0-1 整数规划的解法,是比较重要的内容。
相关文章:

【管理运筹学】第 5 章 | 整数规划 (2,割平面法及 0-1 变量的特性)
文章目录 引言三、割平面法四、0-1 型整数规划4.1 0-1 变量的特性4.1.1 投资问题4.1.2 约束条件满足个数问题 写在最后 引言 前文我们介绍了整数规划的一种求解方法——分支定界法,可以求解纯整数和混合整数规划问题。现在我们来学习另一种整数规划求解方法——割平…...
Vscode详细安装教程
Vscode官网下载 官网地址:Download Visual Studio Code - Mac, Linux, Windows 通过链接可以直接跳转到下面的页面当中,支持的版本有Windows、Linux、Mac,可以选择适配自己电脑的版本,一般来说应该是Windows x64的。不要直接点W…...
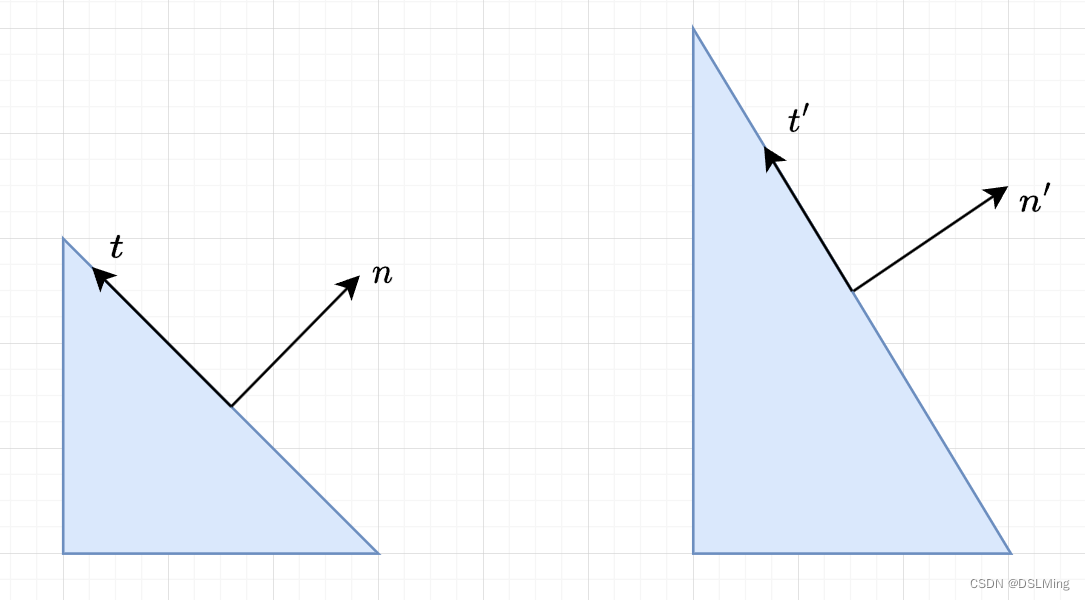
法线矩阵推导
法线矩阵推导 https://zhuanlan.zhihu.com/p/72734738 https://juejin.cn/post/7113952418613690382 https://blog.csdn.net/wangjianxin97?typeblog 1、为什么需要法线矩阵 vec3 normalEyeSpace modelViewMatrix * normal;如果模型矩阵执行了非等比缩放, 顶点的改变会导致法…...
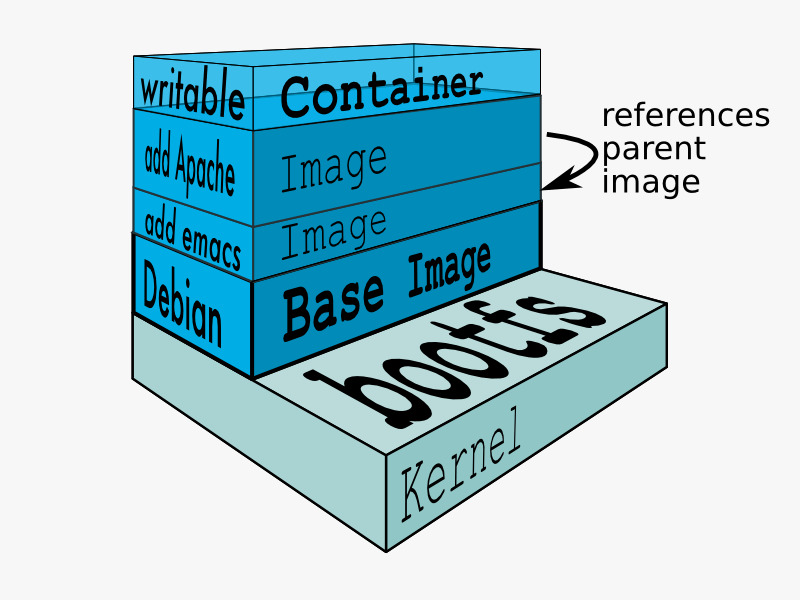
对容器、虚拟机和 Docker 的初学者友好介绍
一、说明 如果你是一个程序员或技术人员,你可能至少听说过Docker:一个有用的工具,用于在“容器”中打包,运输和运行应用程序。很难不这样做,这些天它得到了所有的关注 - 来自开发人员和系统管理员。即使是像谷歌、VMwa…...

linux部署clickhouse(单机)
一、下载安装 1.1、下载地址 阿里巴巴开源镜像站-OPSX镜像站-阿里云开发者社区阿里巴巴开源镜像站,免费提供Linux镜像下载服务,拥有Ubuntu、CentOS、Deepin、MongoDB、Apache、Maven、Composer等多种开源软件镜像源,此外还提供域名解析DNS、…...

vue组件注册
组件注册分为全局注册和局部注册 全局注册 在 main.js 或者入口文件中 import { createApp } from vue; import MyComponent from ./components/MyComponent.vue;const app createApp();app.component(my-component, MyComponent);app.mount(#app); 我们首先通过createApp…...
day20 飞机大战射击游戏
有飞行物类 飞行 爆炸 的连环画, 飞行的背景图 , 子弹图, 还有游戏开始 暂停 结束 的画面图。 设计一个飞机大战的小游戏, 玩家用鼠标操作hero飞行机, 射出子弹杀死敌机,小蜜蜂。 敌机可以获得分数&…...
iOS设计规范是什么?都有哪些具体规范
iOS设计规范是苹果为移动设备操作系统iOS制定的设计指南。iOS设计规范的制定保证了苹果应用在外观和操作上的一致性和可用性,从而提高了苹果界面设计的用户体验和应用程序的成功性。本文将从七个方面全面分析iOS设计规范。 1.iOS设计规范完整版分享 由「即时设计」…...

动手学深度学习-pytorch版本(二):线性神经网络
参考引用 动手学深度学习 1. 线性神经网络 神经网络的整个训练过程,包括: 定义简单的神经网络架构、数据处理、指定损失函数和如何训练模型。经典统计学习技术中的线性回归和 softmax 回归可以视为线性神经网络 1.1 线性回归 回归 (regression) 是能为一个或多个…...
Spark 图计算ONEID 进阶版
0、环境信息 本文采用阿里云maxcompute的spark环境为基础进行的,搭建本地spark环境参考搭建Windows开发环境_云原生大数据计算服务 MaxCompute-阿里云帮助中心 版本spark 2.4.5,maven版本大于3.8.4 ①配置pom依赖 详见2-1 ②添加运行jar包 ③添加配置信…...

Comparable和Comparator区别
Comparable和Comparator接口都是实现集合中元素的比较、排序的,众所周知,诸如Integer,double等基本数据类型,java可以对他们进行比较,而对于类的比较,需要人工定义比较用到的字段比较逻辑。总体来讲&#x…...

JAVA知识点梳理
我的博客:lcatake_flume,spark,zookeeper-CSDN博客 看不懂的话进去看看 1.Java的三个版本 JAVASE 基本 JAVAME 微缩 JAVAEE 标准 3.java的特点 面向对象 跨平台:jvm将java文件转变为字节码文件(.class)在多个系统中运 行字…...
[SWPUCTF 2022 新生赛]ez_ez_php
这段代码是一个简单的PHP文件处理脚本。让我们逐行进行分析: error_reporting(0); - 这行代码设置了错误报告的级别为0,意味着不显示任何错误。 if (isset($_GET[file])) { - 这行代码检查是否存在一个名为"file"的GET参数。 if ( substr($_…...
GraphQL strawberry的使用回顾和体会
GraphQL vs RESTful 简单来说GraphQL 比起 RESTful 集成额外一些功能 出入参校验、序列化 (简化后端编程)自由可选的返回数据字段 (简化一些多余接口开发和沟通联调成本) 这些都是优点了。 开发效率在项目初期是很重要的,需要快速原型化。 但是后期稳定后&#…...

08无监督学习——聚类
1.什么是聚类任务? 类别:无监督学习 目的:通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础。 1.1K均值聚类 步骤: 随机选取样本作为初始均值向量(初始值:k的值【即几个簇】)分别…...

Python使用OpenCV库对彩色图像进行通道分离
目录 1、解释说明: 2、使用示例: 3、注意事项: 1、解释说明: 在Python中,我们可以使用OpenCV库对彩色图像进行通道分离。通道分离是将彩色图像的每个像素分解为三个通道(红、绿、蓝)的过程。…...

前端面试:【CSS】盒模型、选择器、布局、响应式设计、Flexbox 与 Grid
CSS(层叠样式表)是用于控制网页外观和布局的重要语言。在这篇文章中,我们将深入探讨CSS的基础知识,包括盒模型、选择器、布局、响应式设计,以及弹性盒子(Flexbox)和网格布局(Grid&am…...

深入浅出通过PHP封装根据商品ID获取抖音商品详情数据方法
抖音商城商品详情数据是指商品在抖音商城中的展示信息,包括商品的标题、描述、价格、图片等。商家可以通过商品详情数据了解用户对商品的兴趣和需求,从而进行优化和调整。 商品详情数据还可以帮助商家评估商品的销售情况和市场竞争力,为制定…...
排序(七种排序)
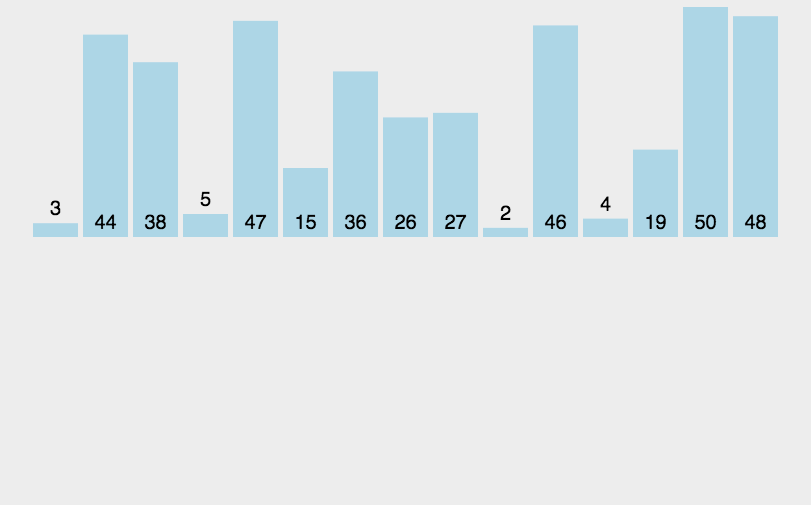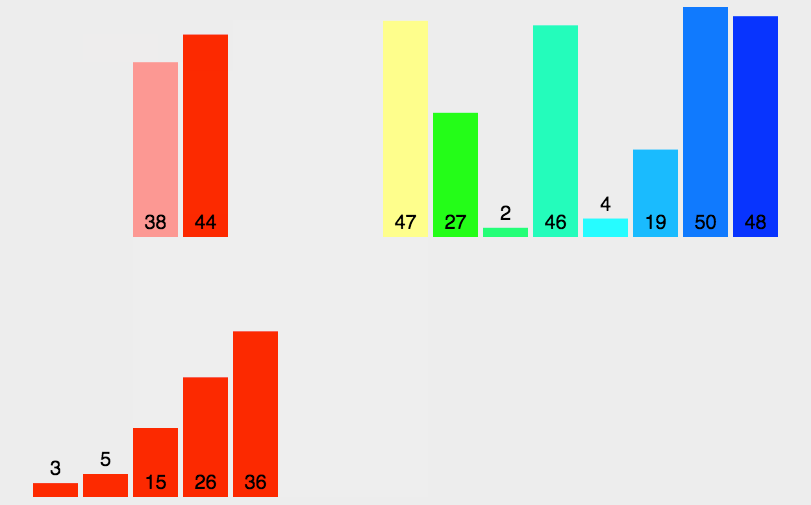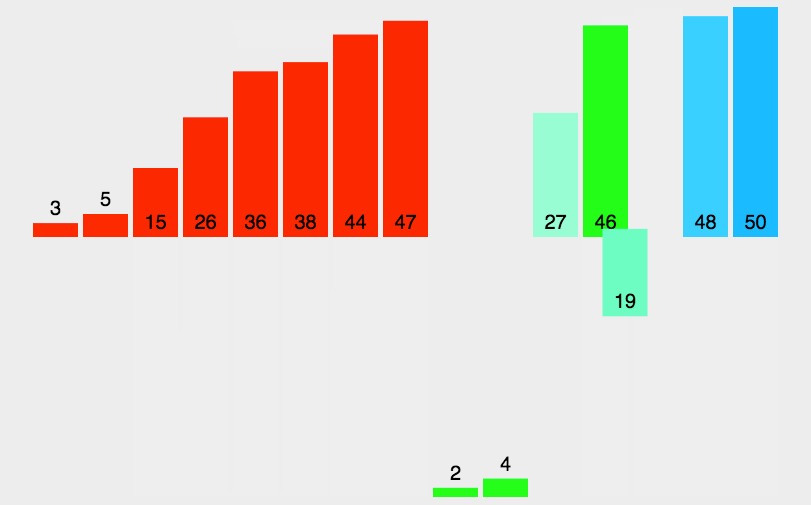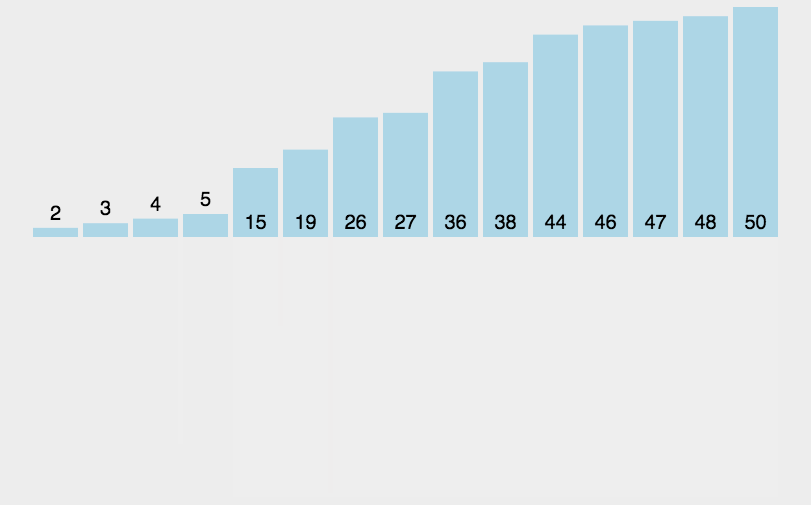
1.插入排序 2.希尔排序 3.选择排序 4.堆排序 5.冒泡排序 6.快速排序 7.归并排序 1.插入排序 1.1思路 把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为 止,得到一个新的有序序列 1.2实现 //插入排…...
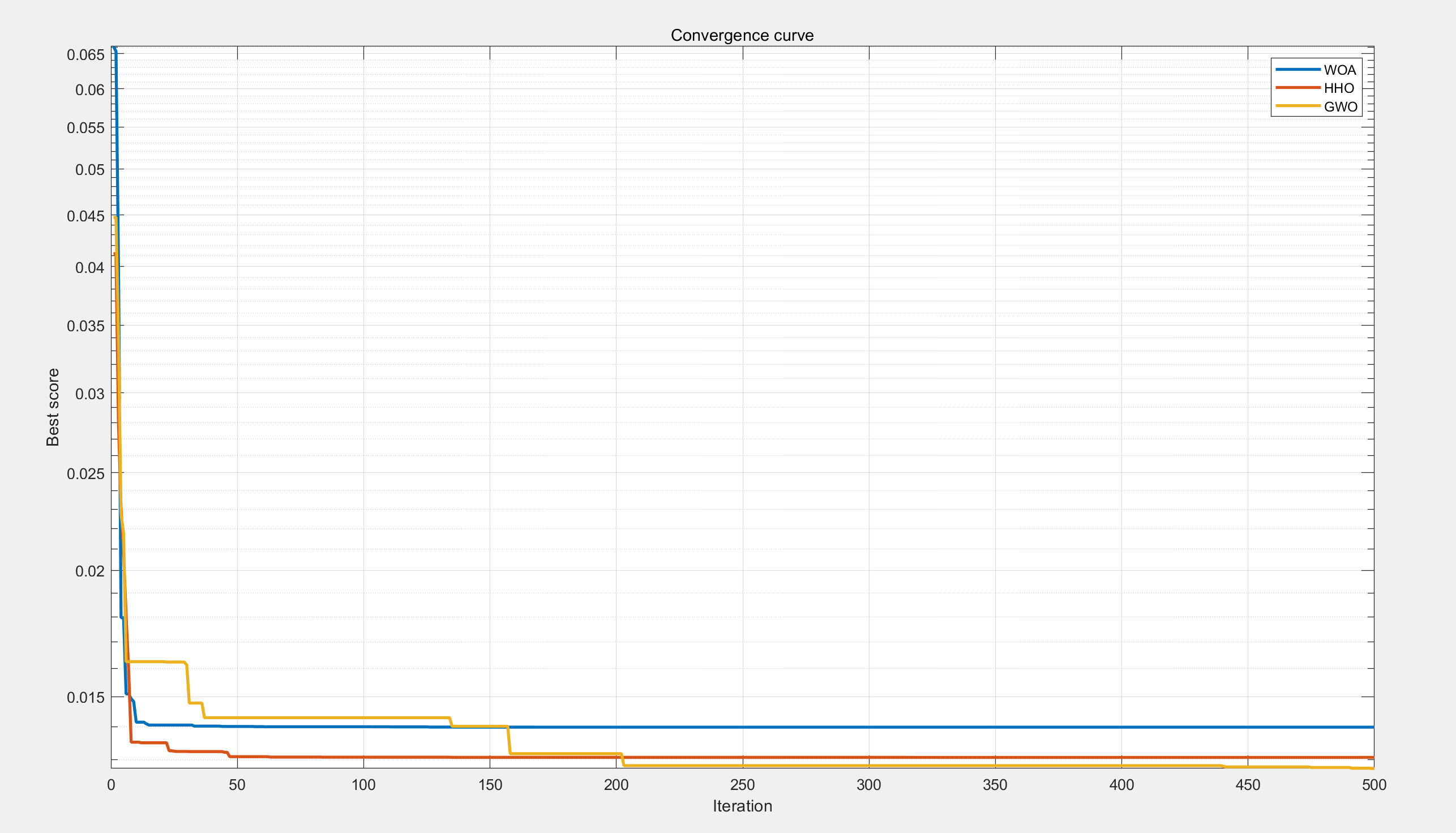
【工程优化问题】基于鲸鱼、萤火虫、灰狼优化算法的张力、压缩弹簧设计问题研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
