分类预测 | Matlab实现SSA-RF和RF麻雀算法优化随机森林和随机森林多特征分类预测
分类预测 |Matlab实现SSA-RF和RF麻雀算法优化随机森林和随机森林多特征分类预测
目录
- 分类预测 |Matlab实现SSA-RF和RF麻雀算法优化随机森林和随机森林多特征分类预测
- 分类效果
- 基本介绍
- 模型描述
- 程序设计
- 参考资料
分类效果






基本介绍
Matlab实现SSA-RF和RF麻雀算法优化随机森林和随机森林多特征分类预测(完整源码和数据)
1.Matlab实现SSA-RF和RF麻雀算法优化随机森林和随机森林多特征分类预测;
2.输入数据为多特征分类数据,即数据输入12个特征,输出分四类;
3.运行环境Matlab2018及以上,运行MainSSA_RF即可,其余为函数文件无需运行,所有程序放在一个文件夹,data为数据集;
4.麻雀算法优化随机森林树木棵树和森林深度,输入12个特征,分四类,可视化展示分类准确率,模型对比输出。
模型描述
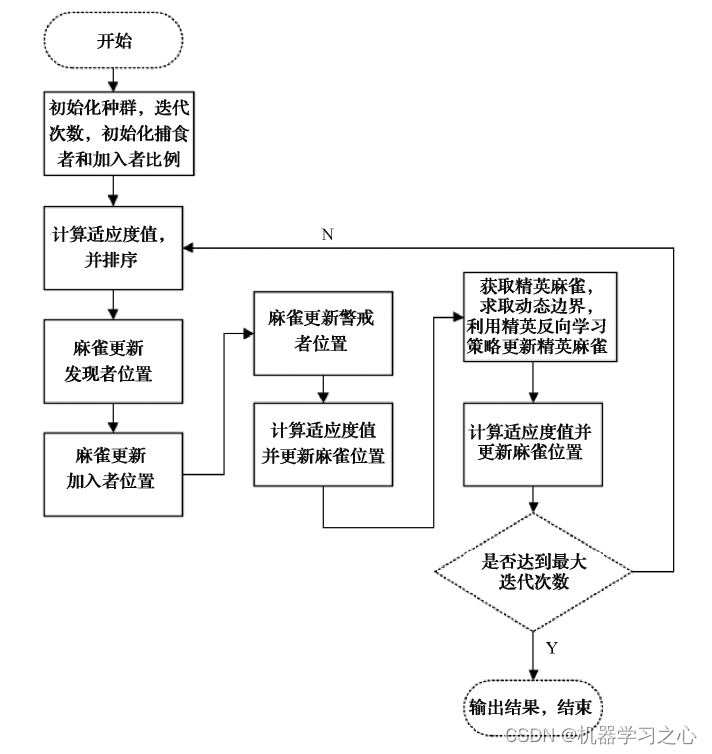
- 麻雀算法
SSA是于2020年提出的,比较新颖,具有寻优能力强,收敛速度快的优点。
首先,对种群初始化。设有n只麻雀组成的种群表示为:


在SSA 中,一部分麻雀作为发现者为种群搜索食物探路。种群中60%的个体作为加入者,依据发现者提供的觅食方向觅食,并且发现者和加入者的身份是动态变化的。最后剩下个体作为警戒者,观察食物周围环境是否有危险,一旦发现危险,立刻发出信号,所有麻雀作出反捕食行为。在每次迭代的过程中,发现者的位置更新描述,如下:

- 随机森林
集成学习常见的独立学习器生成方式有串行序列生成(Boosting)和并行序列生成(Bagging)两种,RF在思想上可以看作是Bagging的改进假设有一个样本集D = {(x1,y1),(x2,y2),…,(x3,y3)},通过自然采样法抽取若干小样本集1,D2,…,DK作为输入训练出C1,C2,…,CK 共K 个弱学习器。再把测试数据导入训练好的弱学习器进行预测分类,通过计算K个弱学习器预测结果的平均值得到最终决策结果。
程序设计
- 完整程序和数据下载方式1:同等价值程序兑换;
- 完整程序和数据下载方式2:Matlab实现SSA-RF和RF麻雀算法优化随机森林和随机森林多特征分类预测
%_________________________________________________________________________%
% 麻雀优化算法 %
%_________________________________________________________________________%
function [Best_pos,Best_score,curve]=SSA(pop,Max_iter,lb,ub,dim,fobj)ST = 0.7;%预警值
PD = 0.4;%发现者的比列,剩下的是加入者0.7
SD = 0.2;%意识到有危险麻雀的比重PDNumber = round(pop*PD); %发现者数量
SDNumber = round(SD*PD);%意识到有危险麻雀数量%种群初始化
X0=initialization(pop,dim,ub,lb);
X = X0;
%计算初始适应度值
fitness = zeros(1,pop);
for i = 1:popfitness(i) = fobj(X(i,:));
end
[fitness, index]= sort(fitness);%升排序
BestF = fitness(1);
WorstF = fitness(end);
GBestF = fitness(1);%全局最优适应度值
for i = 1:popX(i,:) = X0(index(i),:);
end
curve=zeros(1,Max_iter);
GBestX = X(1,:);%全局最优位置
X_new = X;
for i = 1: Max_iterdisp(['第',num2str(i),'次迭代'])BestF = fitness(1);WorstF = fitness(end);R2 = rand(1);for j = 1:PDNumberif(R2<ST)X_new(j,:) = X(j,:).*exp(-j/(rand(1)*Max_iter));elseX_new(j,:) = X(j,:) + randn()*ones(1,dim);end endfor j = PDNumber+1:pop
% if(j>(pop/2))if(j>(pop - PDNumber)/2 + PDNumber)X_new(j,:)= randn().*exp((X(end,:) - X(j,:))/j^2);else%产生-1,1的随机数A = ones(1,dim);for a = 1:dimif(rand()>0.5)A(a) = -1;endend AA = A'*inv(A*A'); X_new(j,:)= X(1,:) + abs(X(j,:) - X(1,:)).*AA';endendTemp = randperm(pop);SDchooseIndex = Temp(1:SDNumber); for j = 1:SDNumberif(fitness(SDchooseIndex(j))>BestF)X_new(SDchooseIndex(j),:) = X(1,:) + randn().*abs(X(SDchooseIndex(j),:) - X(1,:));elseif(fitness(SDchooseIndex(j))== BestF)K = 2*rand() -1;X_new(SDchooseIndex(j),:) = X(SDchooseIndex(j),:) + K.*(abs( X(SDchooseIndex(j),:) - X(end,:))./(fitness(SDchooseIndex(j)) - fitness(end) + 10^-8));endend%边界控制for j = 1:popfor a = 1: dimif length(ub)>1if(X_new(j,a)>ub(a))X_new(j,a) =ub(a);endif(X_new(j,a)<lb(a))X_new(j,a) =lb(a);endelseif(X_new(j,a)>ub)X_new(j,a) =ub;endif(X_new(j,a)<lb)X_new(j,a) =lb;endendendend %更新位置for j=1:popfitness_new(j) = fobj(X_new(j,:));endfor j = 1:popif(fitness_new(j) < GBestF)GBestF = fitness_new(j);GBestX = X_new(j,:); endendX = X_new;fitness = fitness_new;%排序更新[fitness, index]= sort(fitness);%排序BestF = fitness(1);WorstF = fitness(end);for j = 1:popX(j,:) = X(index(j),:);endcurve(i) = GBestF;disp(['current iteration is: ',num2str(i), ', best fitness is: ', num2str(GBestF)]);
end
Best_pos =GBestX; %全局最优位置 K Alpha值组合
Best_score = curve(end);%全局最优适应度值 熵值最小
end
参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/128589064?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128577926?spm=1001.2014.3001.5502
相关文章:

分类预测 | Matlab实现SSA-RF和RF麻雀算法优化随机森林和随机森林多特征分类预测
分类预测 |Matlab实现SSA-RF和RF麻雀算法优化随机森林和随机森林多特征分类预测 目录分类预测 |Matlab实现SSA-RF和RF麻雀算法优化随机森林和随机森林多特征分类预测分类效果基本介绍模型描述程序设计参考资料分类效果 基本介绍 Matlab实现SSA-RF和RF麻雀算法优化随机森林和随机…...
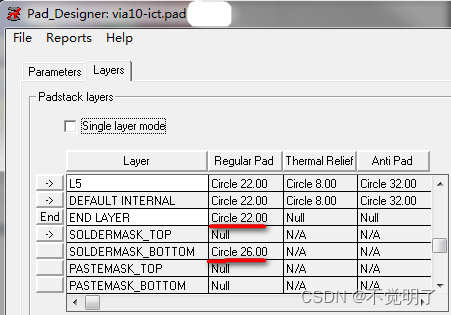
Allegro如何添加ICT操作指导
Allegro如何添加ICT操作指导 当PCB板需要做飞针测试的时候,通常需要在PCB设计的时候给需要测试的网络添加上ICT。 如图: Allegro支持给网络添加ICT,具体操作如下 首先在库中创建一个阻焊开窗的过孔,比如via10-ict一般阻焊开窗的尺寸比盘单边大2mil 在PCB中选择Manufacture…...

软件架构设计(二)——领域架构、基于架构的软件开发方法
目录 一、架构描述语言 ADL 二、特定领域软件架构 DSSA 三、DSSA的三层次架构模型 . 四、基于架构的软件开发方法 (1)基于架构的软件设计(ABSD) (2)开发过程 一、架构描述语言 ADL ADL是一种形式化语言,它在底层语义模型的支持下,为软件系统概念体…...
---数组遍历方法)
数组常用方法(2)---数组遍历方法
1. forEach(cb) 回调函数中有三个参数,第一个是当前遍历项(必须),第二个是索引,第三个是遍历的数组本身。forEach() 对于空数组不会执行回调函数。forEach()不会使用回调函数的返回值,返回值为undefined。…...
卸载Node.js
0 写在前面 无论您是因为什么原因要卸载Node.js都必须要卸载干净。 请阅读: 1 卸载步骤 1.1通过控制面板卸载node.js winR—>control.exe—>卸载程序—>卸载Node.js 等待—>卸载成功 1.2 删除安装时的nodejs文件夹 通过记忆或者Everthing搜索找…...

发表计算机SCI论文,会经历哪些过程? - 易智编译EaseEditing
一、选期刊。 一定要先选期刊。每本期刊都有自己的特色和方向,如果你的稿子已经成型,再去考虑期刊选择的问题,恐怕后期不是退稿就是要大面积修改稿子。 选期刊的标准没有一定的,主要是各单位都有自己的要求,当然小编…...

python中lambda的用法
1. lambada简单介绍 lambda 在Python编程中使用的频率非常高,我们通常提及的lambda表达式其实是python中的一类特殊的定义函数的形式,使用它可以定义一个匿名函数。即当你需要一个函数,但又不想费神去命名一个函数,这时候…...
网络安全协议(3)
作者简介:一名在校云计算网络运维学生、每天分享网络运维的学习经验、和学习笔记。 座右铭:低头赶路,敬事如仪 个人主页:网络豆的主页 目录 前言 一.当前流行操作系统的安全等级 1.Windows的安全等级 什么是EAL…...

102.第十九章 MySQL数据库 -- MySQL的备份和恢复(十二)
5.备份和恢复 5.1 备份恢复概述 5.1.1 为什么要备份 灾难恢复:硬件故障、软件故障、自然灾害、黑客攻击、误操作测试等数据丢失场景 参考链接: https://www.toutiao.com/a6939518201961251359/ 5.1.2 备份类型 完全备份,部分备份 完全备份:整个数据集 部分备份:只备份数…...
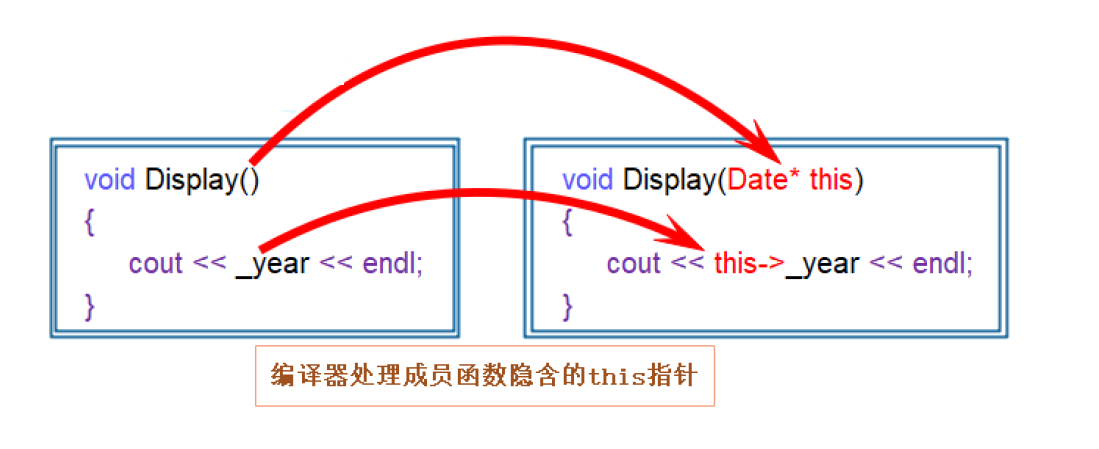
【C++】C++入门 类与对象(一)
类与对象(一)一、类的引入二、类的定义1、类的两种定义方式:2、成员变量命名规则的建议:三、类的访问限定符及封装1、访问限定符2、封装四、类的实例化1、类的实例化概念2、类对象的大小的计算五、this指针this指针的特性一、类的…...

笔记_js运算符
目录二进制相关运算符移位运算符<<>>|(位或运算)参考文档二进制相关运算符 移位运算符 移位运算就是对二进制进行有规律的移位。 tips:进制转换文档链接 << “<<”运算符执行左移位运算。在移位运算过程中,符号位始终保持不变…...
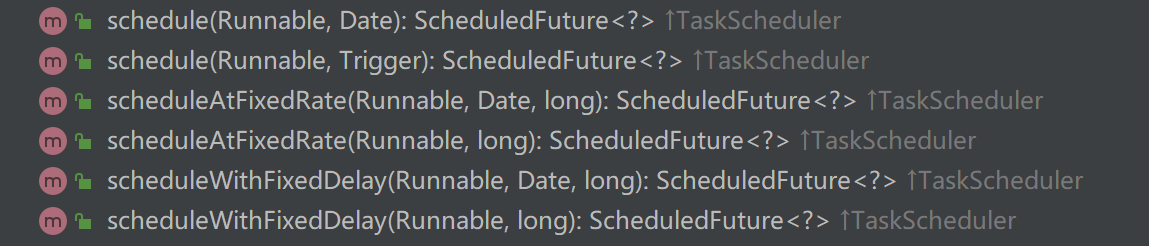
java面试题(十九) Mybatis
4.1 谈谈MyBatis和JPA的区别 参考答案 ORM映射不同: MyBatis是半自动的ORM框架,提供数据库与结果集的映射; JPA(默认采用Hibernate实现)是全自动的ORM框架,提供对象与数据库的映射。 可移植性不同&…...

Linux系统位运算函数以及相应CPU ISA实现收录
以32位数据的二进制表示为例,习惯的写法是LSB在左,MSB在右,注意BIT序和大小端的字节序没有关系。Linux和BIT操作有关的接口在定义在头文件bitops.h中,bitops.h定义有两层,通用层和架构层,对应两个bitops.h&…...

logback配置文件---logback.xml
目录常识操作logback-spring.xml 示例参考于 https://blog.csdn.net/white_ice/article/details/85065219 https://blog.csdn.net/weixin_42592282/article/details/122109703 https://www.dianjilingqu.com/629077.html 常识 https://www.dianjilingqu.com/629077.html nod…...

Web前端-设计网站公共header
设计网站公共headerheader元素是一个具有引导和导航作用的结构元素,很多企业网站中都有一个非常重要的header元素,一般位于网页的开头,用来显示企业名称、企业logo图片、整个网站的导航条,以及Flash形式的广告条等。在本网站中&am…...

引用和指针傻傻分不清
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 目录 🐰引用和指针的区别 🌸从现象上看 🌸从编译上看 &am…...
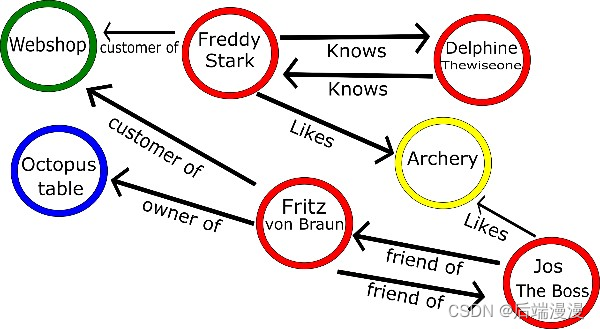
MySQL面试题:关系型数据库SQL和非关系型数据库NoSQL
文章目录一、四大非关系型数据库与关系型数据库的对比1. 关系型数据库2. 基于列的数据库3. 键值对存储4. 文档存储5. 图形数据库参考文章(金文):四大非关系型数据库类型,你知道多少 参考文章:“行式存储”和“列式存储…...
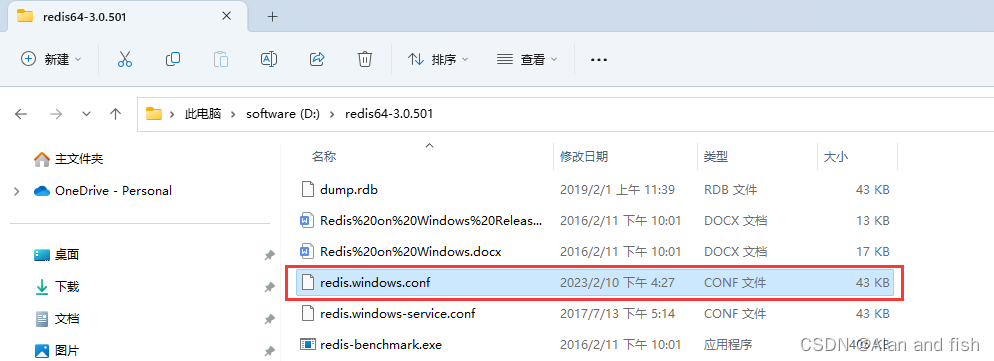
1.Redis【介绍与安装】
1.常用数据库介绍 mysql的表类型[表引擎.存储引擎],memory表结构和表数据分开存储的,表结构保存在硬盘中,表数据保存在内存中memcache是一款软件,可以使用键值对的格式保存数据到内存中redis是意大利的工程师开发的开源免费的告诉缓存数据库,需要注意的是作者本身只开发了linu…...

DataStore快速上手1-preference
DataStore 概念 DataStore 可以存储两种类型的数据,一种是 preference,一种是 protobuf 每个进程在同一时间内仅能打开一个 DataStore 实例(或者通过其他管理手段来实现多个 DataStore 交替使用) 一个 DataStore 可以视为一张数…...

彻底掌握 MySQL InnoDB 的锁机制
本文是对沈剑大佬锁机制十多篇文章的概括总结,文末有全部链接,还参考了 10 多位其他网友的优秀分享。 1、概要 MySQL 中的锁可以按照粒度分为锁定整个表的表级锁(table-level locking)和锁定数据行的行级锁(row-level locking): 表级锁具有开…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
