软件设计(十三)-原码、反码、补码、移码
软件设计(十二)数据结构(下) https://blog.csdn.net/ke1ying/article/details/129035300
https://blog.csdn.net/ke1ying/article/details/129035300
下面把一个数转成二进制表达形式
原码:
数值1 : 0000 0001
数值-1 : 1000 0001
1 + (- 1) : 1000 0010
这是8个bit,其中首位代表符号,0代表正数,1代表负数。相加后等于-2,这显然是不对的。 所以原码不能在机器里直接相关运算。
范围:-127~127
反码:
数值1: 0000 0001
数值-1: 1111 1110
1 +(-1):1111 1111
正数则反码和原码一致,负数除了符号位,其他位置取反,这时候相加等于-0。(为什么等于-0,首位1不变,代表-数,后面7个1取反,则是1000 0000,所以代表-0)
范围:-127~127
补码:
数值1: 0000 0001
数值-1: 1111 1111
1+(-1):0000 0000
正数不变,负数尾数加1,这时候就算出是0。
范围:-128~127
移码:(一般作用于浮点运算当中的解码)
数值1: 1000 0001
数值-1: 0111 1111
1+(-1):1000 0000
首位在补码的基础上取反,移码中 1代表正数,0代表负数,所以相加之后还是0。
- 表达式采用逆波兰式表示时,利用(栈)进行求值。
逆波兰表达式是把运算符号写在对象的后面,例如a+b写成ab+,所以也称后缀式。
- 网络管理员通过命令行方式对路由器进行管理,需要确保ID、口令和会话内容的保密性,应采用的访问方式是 SSH。
SHH是建立在应用层和传输层基础上的安全协议。SSH(Secure Shell)
相关文章:
软件设计(十三)-原码、反码、补码、移码
软件设计(十二)数据结构(下)https://blog.csdn.net/ke1ying/article/details/129035300 下面把一个数转成二进制表达形式 原码: 数值1 : 0000 0001 数值-1 : 1000 0001 1 (- 1) : 1000 0010 这是8个…...
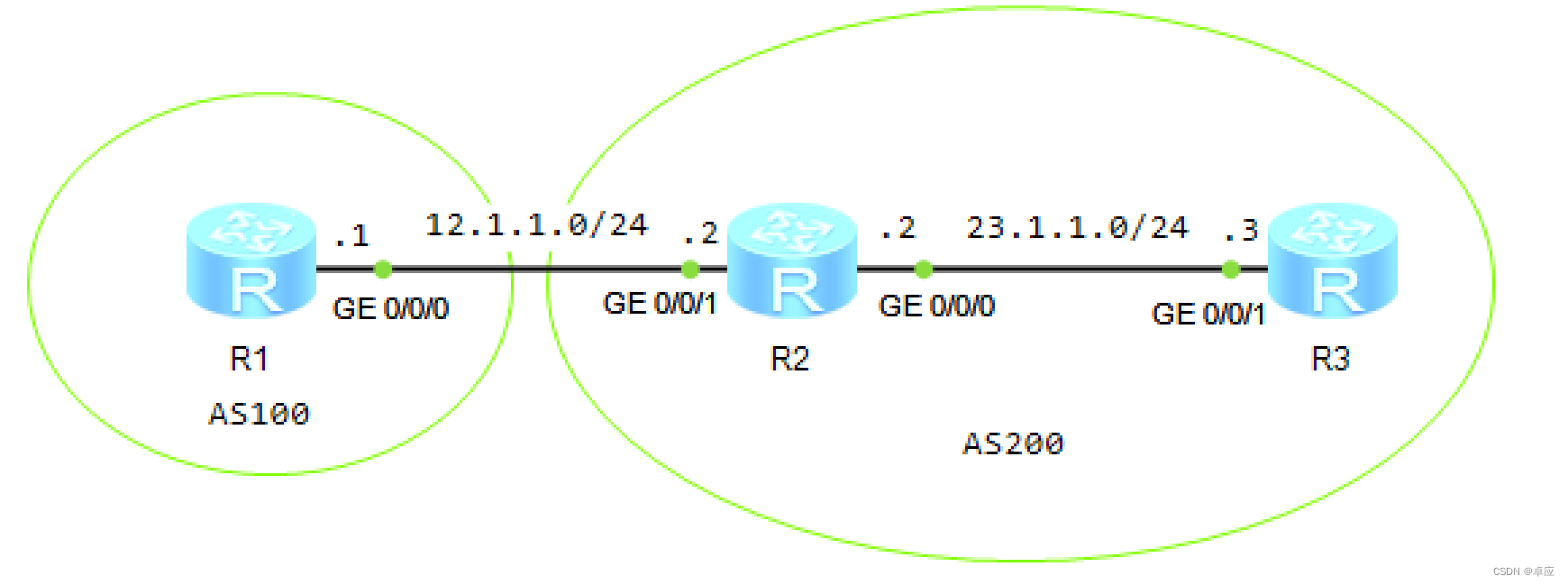
5.4 BGP地址聚合
5.3.1配置BGP地址聚合 1. 实验目的 熟悉BGP地址聚合的应用场景掌握BGP地址聚合的配置方法2. 实验拓扑 实验拓扑如图5-4所示: 图5-4:配置BGP地址聚合 3. 实验步骤 (1)配置IP地址 R1的配置 <Huawe…...
 | 机试题算法思路 【2023】)
华为OD机试 - 数列还原(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 自动曝光(Python) | 机试题算法思路 【2023】 华为OD机试 - 双十一(Python) | 机试题算法思路 【2023】 华为OD机试 - 删除最少字符(Python) | 机试题算法思路 【2023-02】 华为OD机试 - Excel 单元格数值统计(Python) | 机试题算法思路 …...
| 代码+思路+重要知识点)
华为OD机试题 - 新工号系统(JavaScript)| 代码+思路+重要知识点
最近更新的博客 华为OD机试题 - 字符串加密(JavaScript) 华为OD机试题 - 字母消消乐(JavaScript) 华为OD机试题 - 字母计数(JavaScript) 华为OD机试题 - 整数分解(JavaScript) 华为OD机试题 - 单词反转(JavaScript) 使用说明 参加华为od机试,一定要注意不要完全背…...

Java-算法竞赛中常用的Java API之大数类
Java-算法竞赛中常用的Java API之大数类摘要BigInteger和BigDecimal创建赋值加法减法乘法除法*取余*求最大公因数求最值*(a^b)%mod比较大小*进制转化类型转化BigDecimal精度问题保留n位小数摘要 java中的基础数据类型能存储的最大的二进制数是 2 ^ 63 - 1, 对应的十进制数是92…...

了解Nginx,这一篇就够了
了解Nginx,这一篇就够了1.Nginx应用场景2.Nginx相关概念正向代理和反向代理负载均衡动静分离3.Nginx配置文件解析全局块events块http块1.Nginx应用场景 HTTP服务器:Nginx本身也是一个静态资源的服务器,当只有静态资源的时候,就可…...

k8s删除pod或deployment
查看pod或者deployment信息 deployment: kubectl get deployment -n 命名空间pod: kubectl get pod -n 命名空间删除pod或者deployment 删除pod: kubectl delete pod <pod名> -n <命名空间>可是,此时你会发现刚刚…...

Visual Studio 2022: 增加对虚幻引擎的支持
自 Visual Studio 2022 发布以来,我们一直专注于为游戏和大型项目开发人员提供一系列生产力和性能改进。今天,我们很高兴与大家分享下一组专门用来提高虚幻引擎开发效率的功能。我们听到并看到了来自你(我们的游戏开发人员)的大量…...

【Python】以邮件的方式定时发送一天的股票分析报告
【Python】以邮件的方式定时发送一天的股票分析报告 文章目录【Python】以邮件的方式定时发送一天的股票分析报告1、Python发送邮件1)EmailSender封装2)可能存在的问题2、jinja2动态渲染html页面3、阿里云OSS搭建图床1)Python上传图片到OSS中…...

mybatis条件构造器(二)
mybatis条件构造器(二) 1 准备工作 1.1 建表sql语句(Emp表) SET NAMES utf8mb4; SET FOREIGN_KEY_CHECKS 0;-- ---------------------------- -- Table structure for emp -- ---------------------------- DROP TABLE IF EXISTS emp; CREATE TABLE emp (EMPNO int NOT NU…...
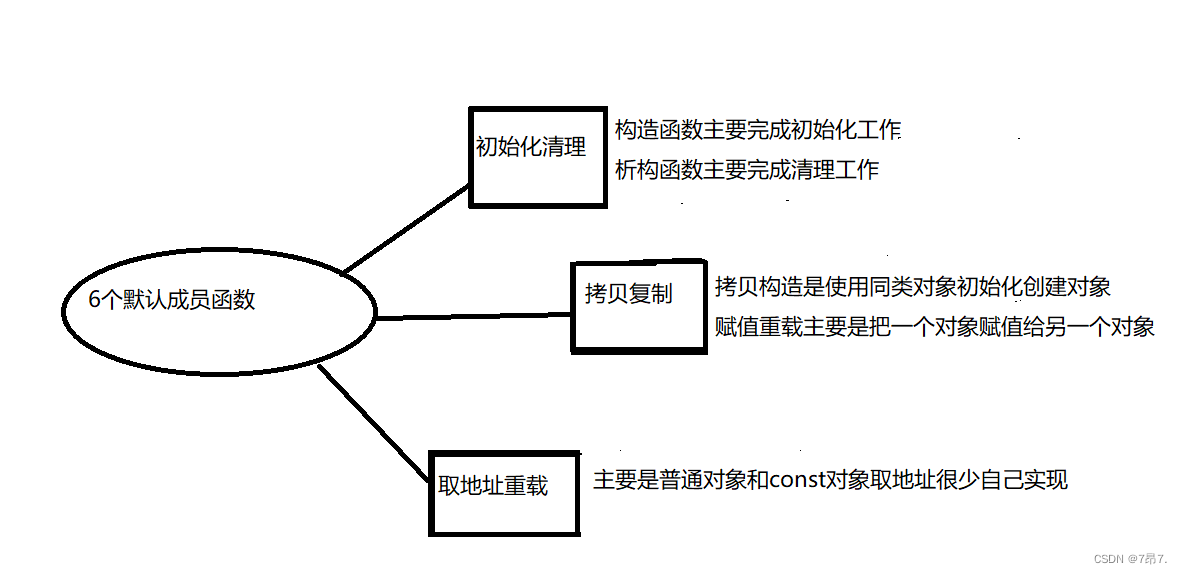
C++【类与对象】
文章目录类与对象(1)类与对象一1.0.面向过程和面向对象初步认识1.1.类的引入1.2.类的定义1.3.类的访问限定符及封装1.4.类的作用域1.5.类的实例化1.6.类的对象大小的计算1.8.类成员函数的this指针(2)类与对象二2.0类的6个默认成员…...

假设检验选择统计量重点-----正态总体参数的假设检验
文章目录单个正态总体参数的假设检验单个正态总体N(μ,σ2)N(\mu,\sigma^2)N(μ,σ2)的均值μ\muμ的假设检验1.σ2\sigma^2σ2已知(U检验法)单个正态总体方差的假设检验单边检验简介--计算拒绝域两个正态总体参数的假设检验方差已知的两正态总体均值的假设检验均值未知的两正态…...
 | 机试题算法思路 【2023】)
华为OD机试 - 通信误码(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 自动曝光(Python) | 机试题算法思路 【2023】 华为OD机试 - 双十一(Python) | 机试题算法思路 【2023】 华为OD机试 - 删除最少字符(Python) | 机试题算法思路 【2023-02】 华为OD机试 - Excel 单元格数值统计(Python) | 机试题算法思路 …...

设计模式之装饰者模式
文章の目录一、什么是装饰者模式二、优势三、缺点四、应用场景五、示例参考写在最后一、什么是装饰者模式 装饰者模式也称为包装器模式,在不改变原有对象的基础上为其动态的添加上新的功能。 装饰者模式有以下特点: 添加功能时不改变原对象结构。装饰…...
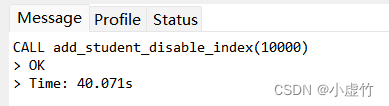
【第31天】SQL进阶-写优化- 插入优化(SQL 小虚竹)
回城传送–》《31天SQL筑基》 文章目录零、前言一、练习题目二、SQL思路:SQL进阶-写优化-插入优化解法插入优化禁用索引语法如下适用数据库引擎非空表:禁用索引禁用唯一性检查语法如下适用数据库引擎禁用外键检查语法如下适用数据库引擎批量插入数据语法…...
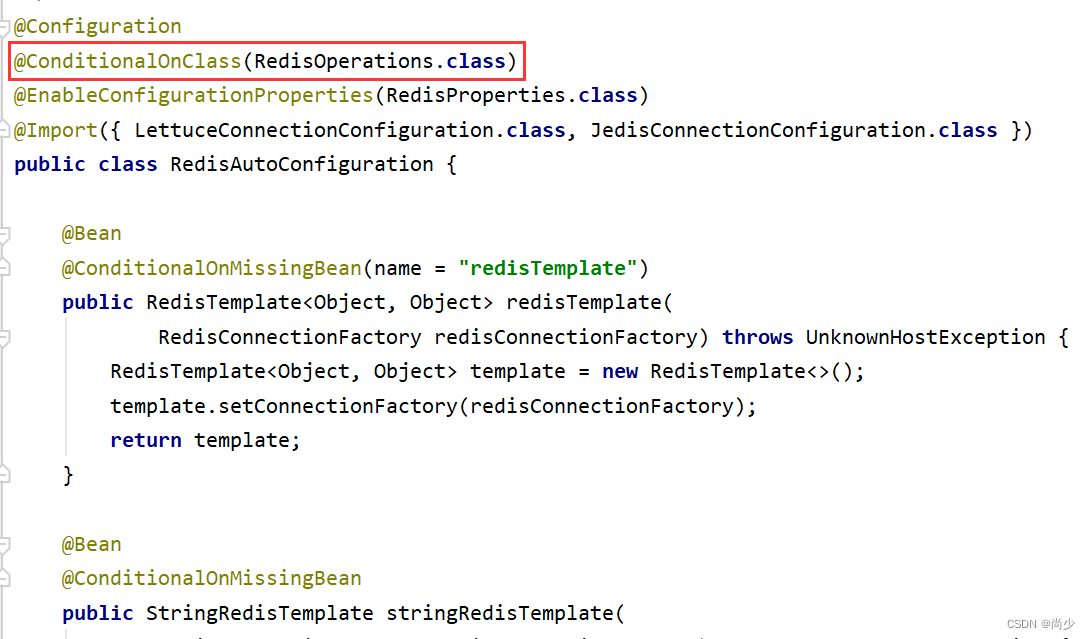
SpringBoot自动装配的原理
前言 在开发SpringBoot项目时,当我们引入spring-boot-starter-xxx依赖后,想要使用依赖中的bean,直接就用Autowired拿来用了,不需要用xml或者注解的方式把它先注入到Spring容器中。这就是自动装配的特性,本文来讲述Spri…...
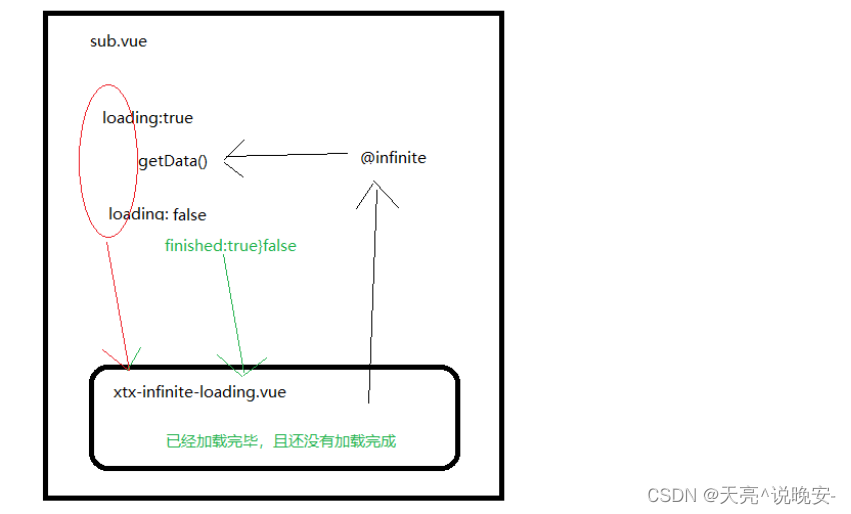
Vue3电商项目实战-分类模块5【12-二级类目-结果区-排序组件、13-二级类目-结果区-数据加载、14-二级类目-结果区-进行筛选】
文章目录12-二级类目-结果区-排序组件13-二级类目-结果区-数据加载14-二级类目-结果区-进行筛选12-二级类目-结果区-排序组件 目的:封装排序组件,完成排序切换效果 大致步骤: 定义一个组件 sub-sort,完成基础布局在 sub.vue 组件…...

计算机操作系统概述
文章目录1.0 操作系统概述1.1 操作系统的目标1.2 操作系统的功能1.3 操作系统结构1.4 操作系统接口1.5 操作系统的发展1.6 操作系统的特征2.0 进程管理2.1 进程调度2.2 进程调度算法2.3 进程间通信2.4 进程间的同步2.5 软件实现互斥的方法2.6 硬件实现互斥的方法2.7 信号2.8 管…...
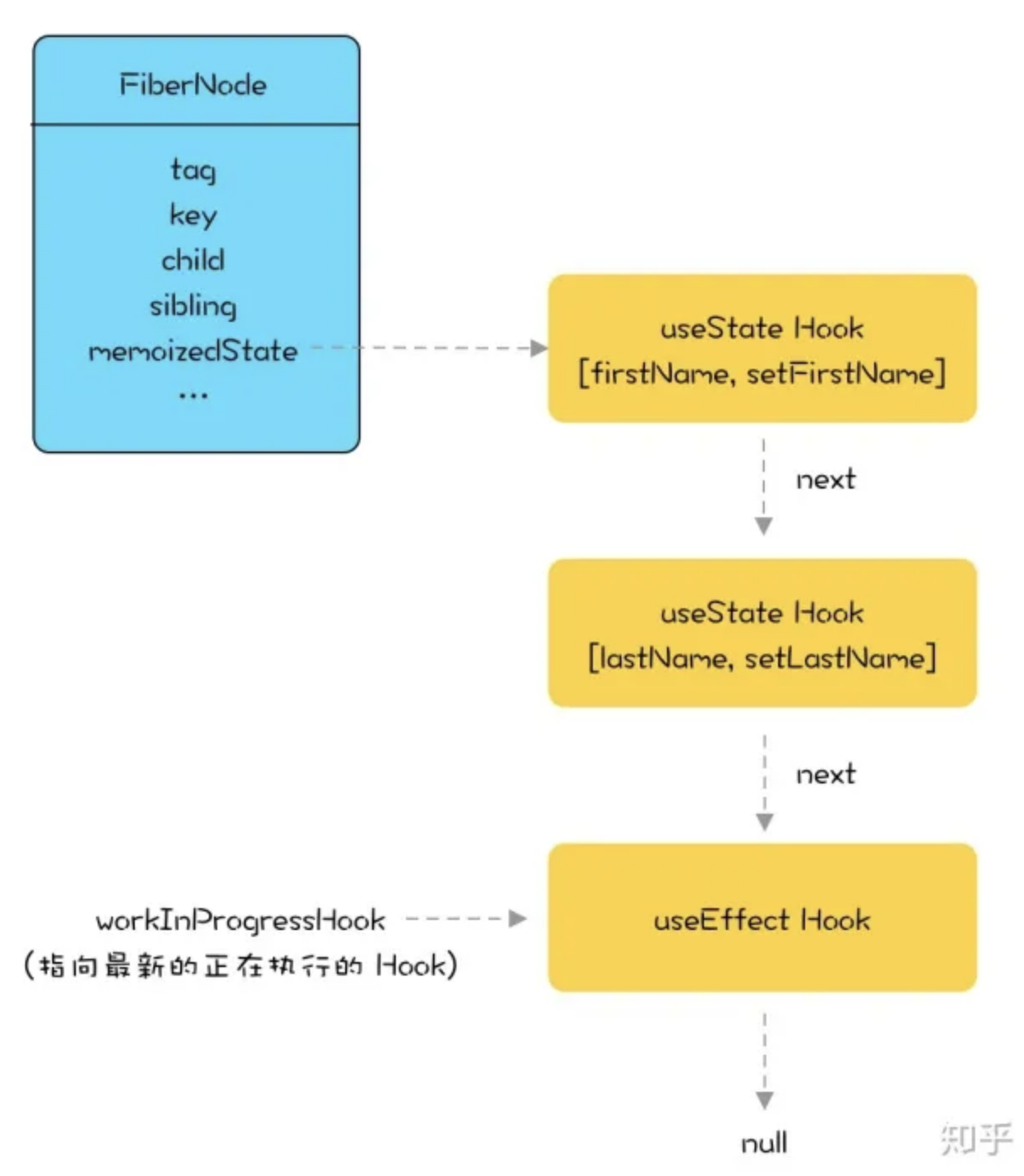
面试官让你说说react状态管理?
hooks 为什么不能放在条件判断里 以 setState 为例,在 react 内部,每个组件(Fiber)的 hooks 都是以链表的形式存在 memoizeState 属性中 update 阶段,每次调用 setState,链表就会执行 next 向后移动一步。如果将 setState 写在条…...

CUDA线程块的分配
为了确保能够真正地了解线程块的分配,接下来我们写一个简短的内核程序来输出线程块、线程、线程束和线程全局标号到屏幕上。现在,除非你使用的是 3.2 版本以上的 SDK否则内核中是不支持 printf的。因此,我们可以将数据传送回 CPU 端然后输出到…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...
