【C++】RBTree——红黑树
文章目录
- 一、红黑树的概念
- 二、红黑树的性质
- 三、红黑树节点的定义
- 四、红黑树的插入
- 五、代码实现

一、红黑树的概念
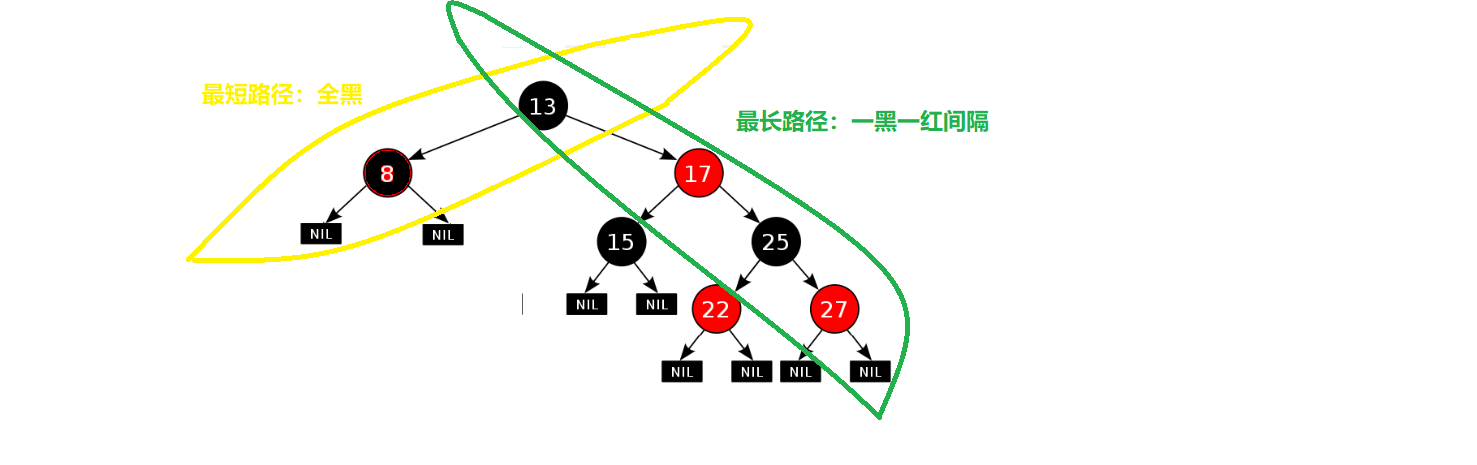
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的 。(既最长路径长度不超过最短路径长度的 2 倍)
ps:树的路径是从根节点走到空节点(此处为NIL 节点)才算一条路径
二、红黑树的性质
-
每个结点不是红色就是黑色
-
根结点是
黑色的 -
如果一个结点是
红色的,则它的两个孩子结点是黑色的(没有连续的红色结点) -
对于每个结点,从该节点到其所有后代叶结点的简单路径上,均包含
相同数目的黑色结点 -
每个叶子结点都是黑色的(此处的叶子结点指的是空节点,NIL节点),如果是空树,空节点也是黑色,符合第一个性质
理解最长路径长度不超过最短路径长度的 2 倍:
根据第三个性质:红黑树不会出现连续的红色结点,根据第四个性质:从每个结点到所有后代结点的路径上包含相同数目的黑色结点。
极端场景:最短路径上全黑,一条路径黑色节点的数量,最长路径上是一黑一红相间的路径
三、红黑树节点的定义
三叉链结构,对比AVL数节点的定义,把平衡因子替换成节点颜色,采用枚举的方式:
//结点颜色
enum Color
{RED,BLACK,
};template<class K, class V >
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Color _col;RBTreeNode(const pair<K,V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED){}
};
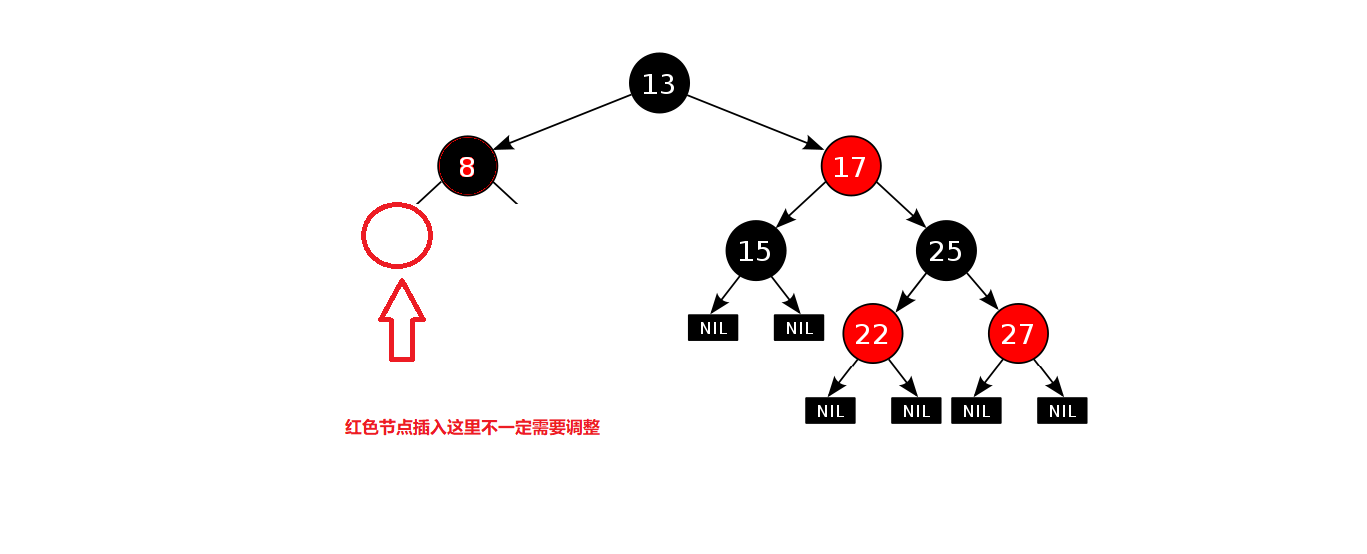
这里可以清楚的看到,构造结点时默认设置为红色,问题来了:
如果插入的是黑色结点那就是不符合第四个性质(路径上均包含相同的黑色结点),此时我们必须要去进行维护每条路径的黑色结点
如果插入的是红色结点那就是不符合第三个性质(没有出现连续的红色结点),但是我们并不一定需要调整,如果根刚好为黑色,就不需要进行调整。
所以如果插入为红色结点,不一定会破坏结构,但是如果插入黑色结点我们就必须去进行维护了
四、红黑树的插入
红黑树插入的操作部分和AVL树的插入一样:
- 找到待插入位置
- 将待插入结点插入到树中
- 调整:若插入结点的父结点是红色的,我们就需要对红黑树进行调整
前两步大差不差
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树分情况来讨论
关键在于对红黑树进行调整:为了能够展示出各种情况,这里有一个基本的模型:
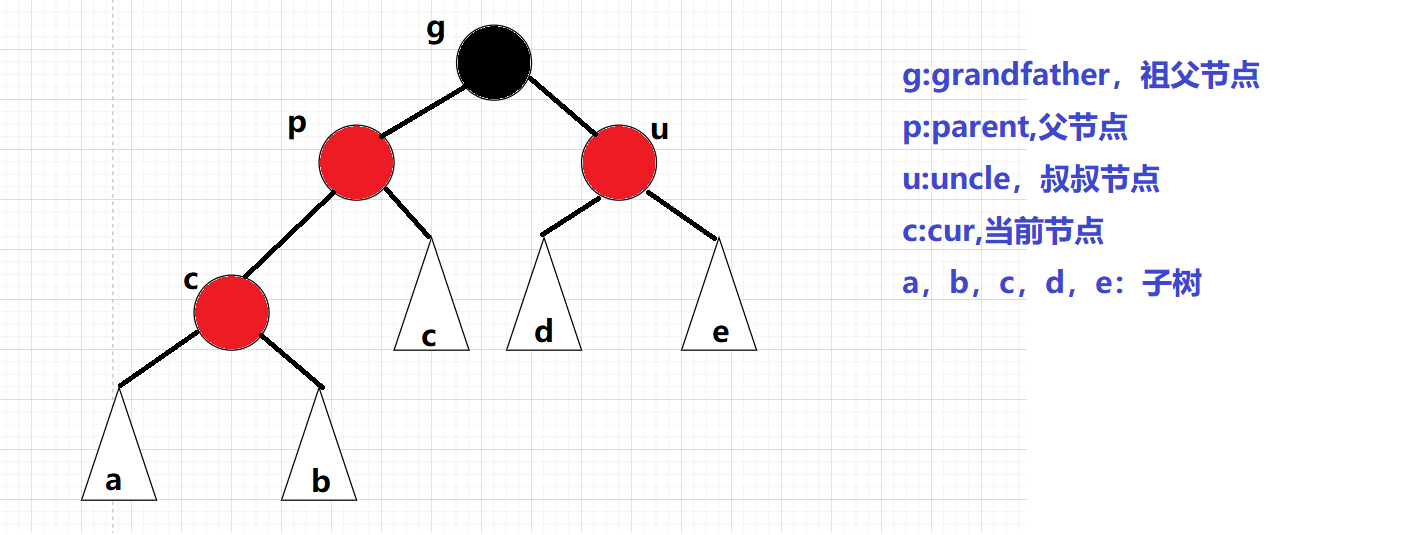
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
情况一:cur为红,p为红,g为黑,u存在且为红 :
cur为红,p为红,g为黑,u存在且为红
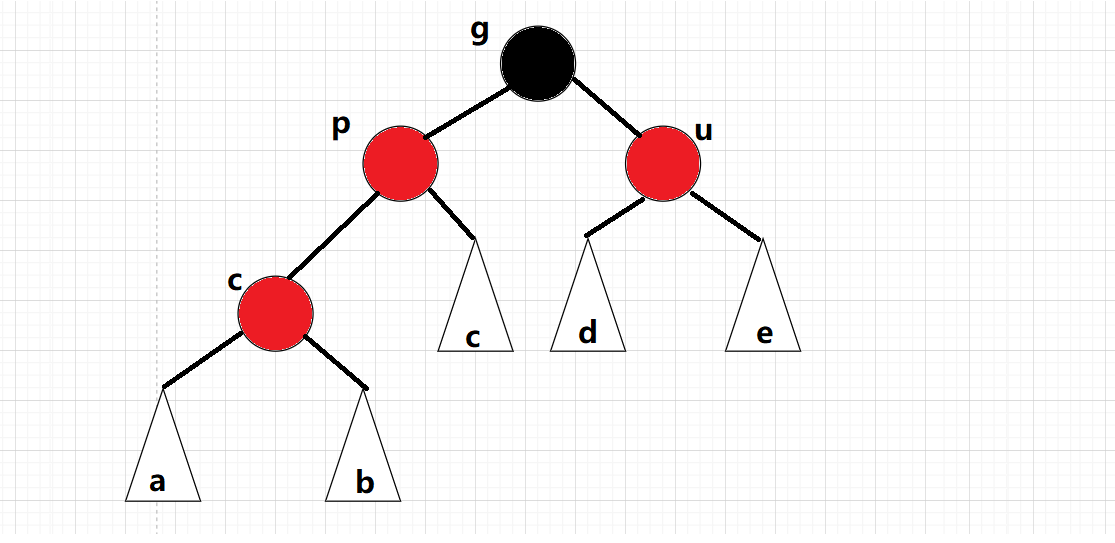
关键看u结点,根结点的颜色为黑色,不能有连续的红色结点,所以上面的情况已经出现连续的红色结点了,此时我们需要进行调整:
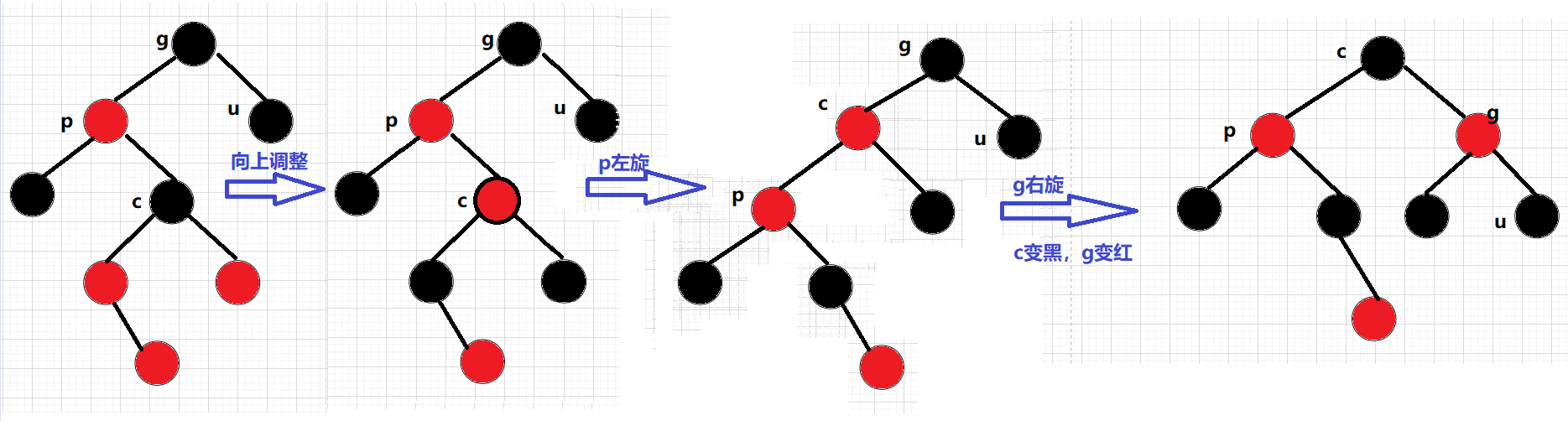
把p结点改为黑色,同时把u结点也改为黑色(符合性质四:每条路径上的黑色节点数量相同),最后在把g结点改为红色;如果g是子树的话,g一定会有双亲,为了维持每条路径上黑色节点的数量,g必须变红,不然会多出一个黑色节点,在把g结点当做cur结点继续往上调整,当g为根结点时,在把g置为黑色:
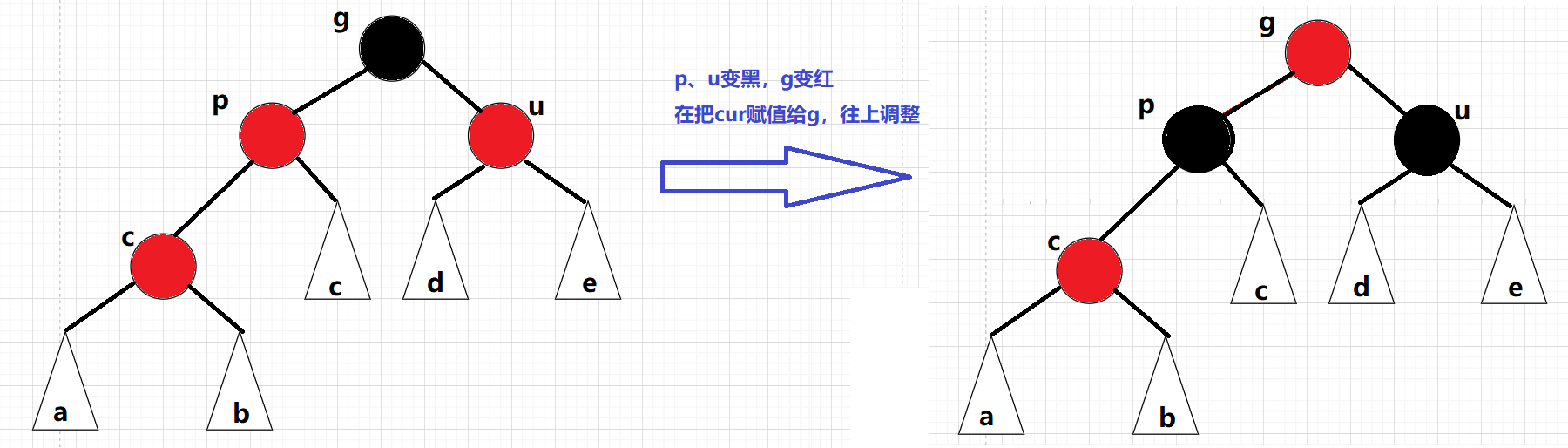
代码实现:
while (parent && parent->_col == RED){Node* grandfater = parent->_parent;if (parent == grandfater->_left){Node* uncle = grandfater->_right;//情况一:u存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfater->_col = RED;cur = grandfater;parent = cur->_parent;}else//其他情况{}}else//parent==grandfater->_right{Node* uncle = grandfater->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfater->_col = RED;cur = grandfater;parent = cur->_parent;}else{}}}_root->_col = BLACK;
情况二:cur为红,p为红,g为黑,u不存在/u为黑,gpc在同一侧:

此时u的情况:
如果u结点不存在,则cur一定是新增结点,因为如果cur不是新增结点:则cur和p一定有一个节点时黑色,就不满足每条路径都有相同的黑色结点的性质。
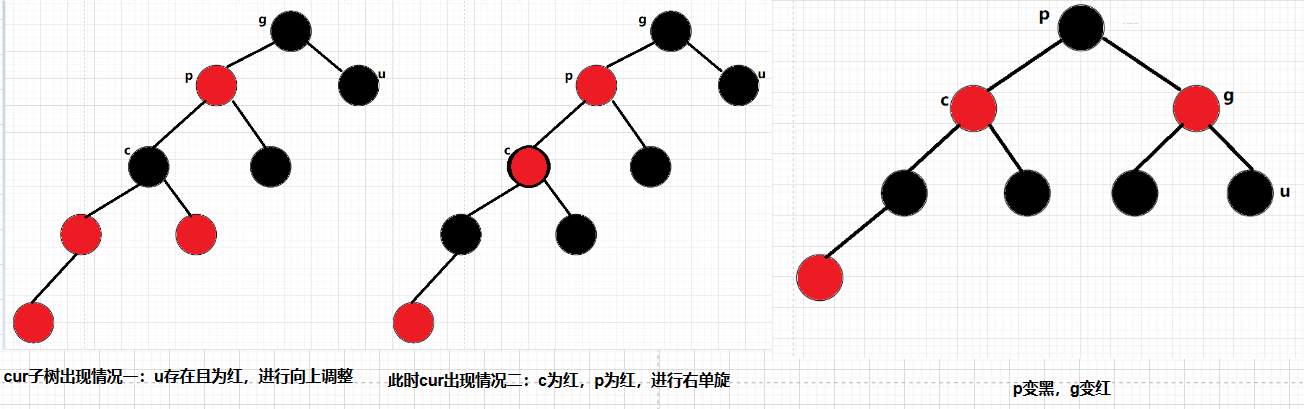
如果u结点存在,则其一定是黑色的,那么c节点原来的颜色一定是黑色,在其子树调整过程中变为了红色
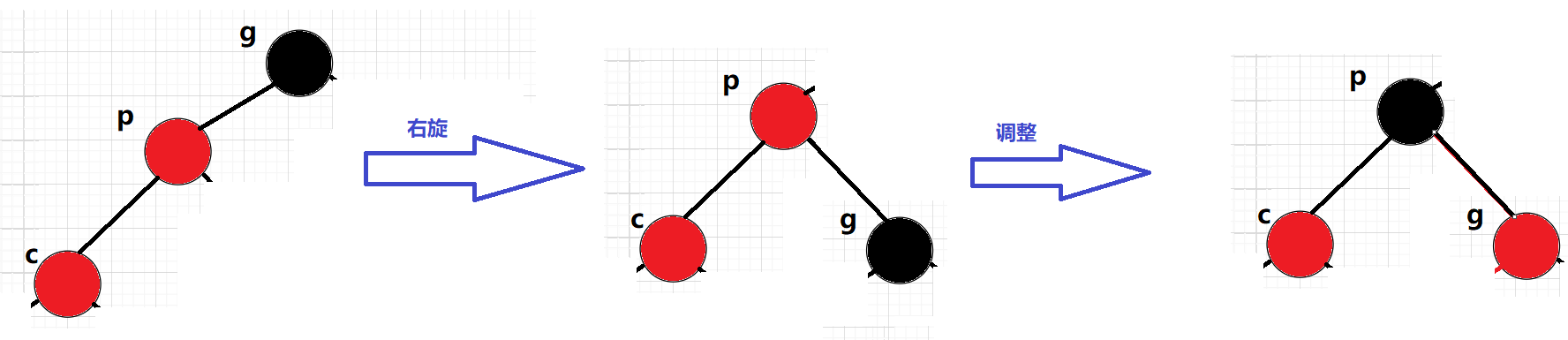
如果p为g的左孩子,cur为p的左孩子,则进行右单旋转;
如果p为g的右孩子,cur为p的右孩子,则进行左单旋转,
同时,p、g变色–p变黑,g变红
以下情况:u不存在,cur为新增节点,进行右单旋:
以下情况:u结点存在且为黑:
情况三: cur为红,p为红,g为黑,u不存在/u为黑,gpc不在同一侧:
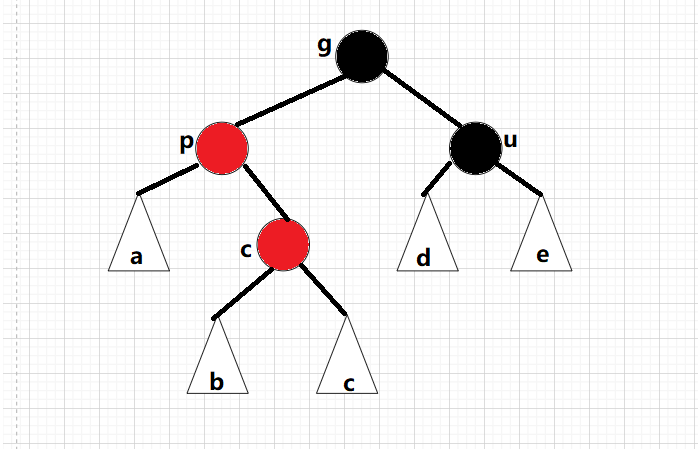
这时候我们就需要进行双旋了:
p为g的左孩子,cur为p的右孩子,对p做左单旋转;
p为g的右孩子,cur为p的左孩子,对p做右单旋转;
旋转之后则转换成了情况2,在继续进行调整即可
五、代码实现
送上源码:
#pragma once
#include <iostream>
#include <assert.h>
#include <time.h>
using namespace std;
enum Color
{RED,BLACK,
};
template<class K, class V >
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Color _col;RBTreeNode(const pair<K,V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED){}
};template<class K,class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED){Node* grandfater = parent->_parent;if (parent == grandfater->_left){Node* uncle = grandfater->_right;//情况一:u存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfater->_col = RED;//向上调整cur = grandfater;parent = cur->_parent;}else{//情况2if (cur == parent->_left){RotateR(grandfater);parent->_col = BLACK;grandfater->_col = RED;}//情况3else{// g// p// c RotateL(parent);RotateR(grandfater);cur->_col = BLACK;grandfater->_col = RED;}break;}}else//parent==grandfater->_right{Node* uncle = grandfater->_left;//情况1:u存在且为红色if (uncle && uncle->_col == RED){uncle->_col = parent->_col = BLACK;grandfater->_col = RED;//向上调整cur = grandfater;parent = cur->_parent;}else{//情况2:u不存在/u存在为黑色//g// p// cif (cur == parent->_right){RotateL(grandfater);grandfater->_col = RED;parent->_col = BLACK;}//情况3// g// p// celse{RotateR(parent);RotateL(grandfater);cur->_col = BLACK;grandfater->_col = RED;}break;}}}//根变黑_root->_col = BLACK;return true;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppNode = parent->_parent;parent->_parent = subL;subL->_right = parent;if (ppNode == nullptr){_root = subL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}void InOrder(){_InOrder(_root);}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}bool Check(Node*root,int blackNum,int ref){if (root == nullptr){//cout << blackNum << endl;if (blackNum != ref){cout << "违反规则:本条路径的黑色结点的数量根最左路径不相等" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则:出现连续的红色结点" << endl;return false;}if (root->_col == BLACK){++blackNum;}return Check(root->_left,blackNum,ref)&& Check(root->_right,blackNum,ref);}bool IsBalance(){if (_root == nullptr){return true;}if (_root->_col != BLACK){return false;}int ref = 0;Node* left = _root;while (left){if (left->_col == BLACK){++ref;}left = left->_left;}return Check(_root,0,ref);}
private:Node* _root = nullptr;
};void TestRBTree1()
{//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };RBTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.InOrder();cout << t.IsBalance() << endl;
}void TestRBTree2()
{srand(time(0));const size_t N = 100000;RBTree<int, int> t;for (size_t i = 0; i < N; i++){size_t x = rand();t.Insert(make_pair(x, x));}cout << t.IsBalance() << endl;}
本篇结束…
相关文章:

【C++】RBTree——红黑树
文章目录一、红黑树的概念二、红黑树的性质三、红黑树节点的定义四、红黑树的插入五、代码实现一、红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上…...

【5G RRC】5G系统消息SIB2介绍
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...

自托管提醒平台Noted Reminders
什么是 Noted Reminders ? Noted 是一个简单的自托管应用程序,用于创建使用 Apprise API 推送到设备的提醒。您可以向几乎每个平台发送消息,包括定时电子邮件! 什么是 Apprise API ? Apprise 允许您向我们今天可用的几乎所有最流…...

LockSupport常用方法源码分析
前言:本文将介绍LockSupport类中的方法和部分源码,以及面试常问到的一个小问题,感兴趣的大佬可以指点下。 希望能够加深自己的印象以及帮助到其他的小伙伴儿们😉😉。 如果文章有什么需要改进的地方还请大佬不吝赐教&am…...

Mybatis Notes
文章目录1 Mybatis 介绍1.1 快速入门2 JDBC2.1 JDBC介绍2.3 JDBC问题分析2.4 Mybatis与JDBC技术对比3 数据库连接池3.1 数据库连接池介绍3.2 数据库连接池产品产品3.3 Druid引入项目4lombok4.1 lombok介绍4.2 lombok使用4.2.1 在pom.xml文件中引入依赖4.2.2 pojo类代码引入1 My…...
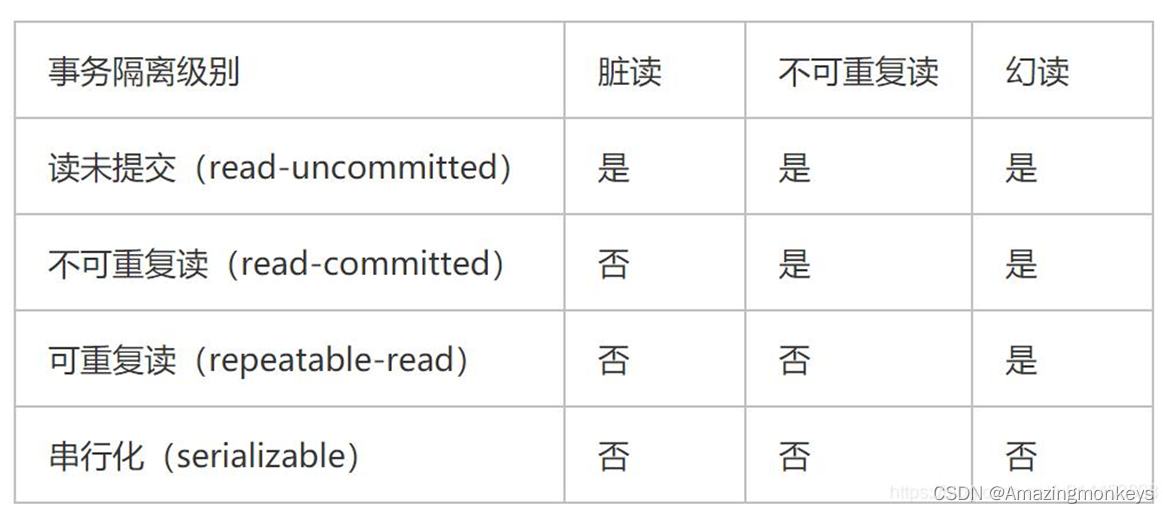
MySQL 10:MySQL事务
MySQL 中的事务是由存储引擎实现的。在 MySQL 中,只有 InnoDB 存储引擎支持事务。事务处理可用于维护数据库的完整性,确保批处理的 SQL 语句要么执行要么根本不执行。事务用于管理 DDL、DML 和 DCL 操作,例如插入、更新和删除语句,…...
软件设计(十三)-原码、反码、补码、移码
软件设计(十二)数据结构(下)https://blog.csdn.net/ke1ying/article/details/129035300 下面把一个数转成二进制表达形式 原码: 数值1 : 0000 0001 数值-1 : 1000 0001 1 (- 1) : 1000 0010 这是8个…...
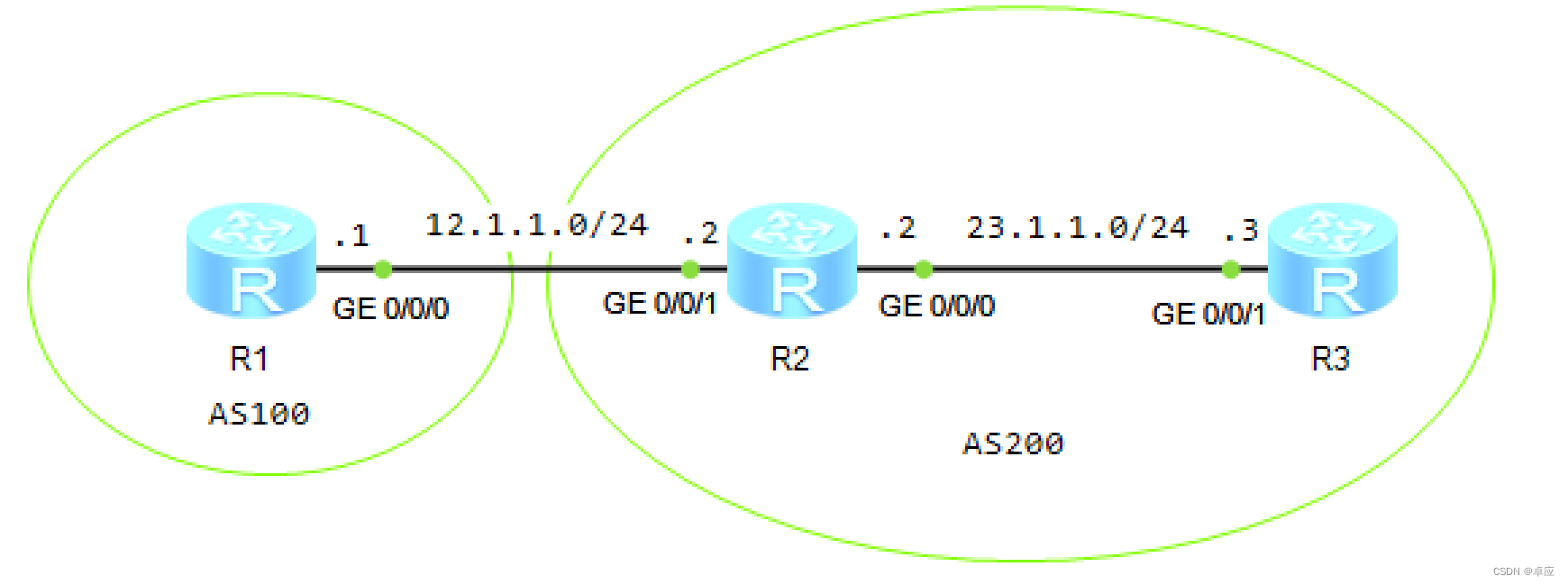
5.4 BGP地址聚合
5.3.1配置BGP地址聚合 1. 实验目的 熟悉BGP地址聚合的应用场景掌握BGP地址聚合的配置方法2. 实验拓扑 实验拓扑如图5-4所示: 图5-4:配置BGP地址聚合 3. 实验步骤 (1)配置IP地址 R1的配置 <Huawe…...
 | 机试题算法思路 【2023】)
华为OD机试 - 数列还原(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 自动曝光(Python) | 机试题算法思路 【2023】 华为OD机试 - 双十一(Python) | 机试题算法思路 【2023】 华为OD机试 - 删除最少字符(Python) | 机试题算法思路 【2023-02】 华为OD机试 - Excel 单元格数值统计(Python) | 机试题算法思路 …...
| 代码+思路+重要知识点)
华为OD机试题 - 新工号系统(JavaScript)| 代码+思路+重要知识点
最近更新的博客 华为OD机试题 - 字符串加密(JavaScript) 华为OD机试题 - 字母消消乐(JavaScript) 华为OD机试题 - 字母计数(JavaScript) 华为OD机试题 - 整数分解(JavaScript) 华为OD机试题 - 单词反转(JavaScript) 使用说明 参加华为od机试,一定要注意不要完全背…...

Java-算法竞赛中常用的Java API之大数类
Java-算法竞赛中常用的Java API之大数类摘要BigInteger和BigDecimal创建赋值加法减法乘法除法*取余*求最大公因数求最值*(a^b)%mod比较大小*进制转化类型转化BigDecimal精度问题保留n位小数摘要 java中的基础数据类型能存储的最大的二进制数是 2 ^ 63 - 1, 对应的十进制数是92…...

了解Nginx,这一篇就够了
了解Nginx,这一篇就够了1.Nginx应用场景2.Nginx相关概念正向代理和反向代理负载均衡动静分离3.Nginx配置文件解析全局块events块http块1.Nginx应用场景 HTTP服务器:Nginx本身也是一个静态资源的服务器,当只有静态资源的时候,就可…...

k8s删除pod或deployment
查看pod或者deployment信息 deployment: kubectl get deployment -n 命名空间pod: kubectl get pod -n 命名空间删除pod或者deployment 删除pod: kubectl delete pod <pod名> -n <命名空间>可是,此时你会发现刚刚…...

Visual Studio 2022: 增加对虚幻引擎的支持
自 Visual Studio 2022 发布以来,我们一直专注于为游戏和大型项目开发人员提供一系列生产力和性能改进。今天,我们很高兴与大家分享下一组专门用来提高虚幻引擎开发效率的功能。我们听到并看到了来自你(我们的游戏开发人员)的大量…...

【Python】以邮件的方式定时发送一天的股票分析报告
【Python】以邮件的方式定时发送一天的股票分析报告 文章目录【Python】以邮件的方式定时发送一天的股票分析报告1、Python发送邮件1)EmailSender封装2)可能存在的问题2、jinja2动态渲染html页面3、阿里云OSS搭建图床1)Python上传图片到OSS中…...

mybatis条件构造器(二)
mybatis条件构造器(二) 1 准备工作 1.1 建表sql语句(Emp表) SET NAMES utf8mb4; SET FOREIGN_KEY_CHECKS 0;-- ---------------------------- -- Table structure for emp -- ---------------------------- DROP TABLE IF EXISTS emp; CREATE TABLE emp (EMPNO int NOT NU…...
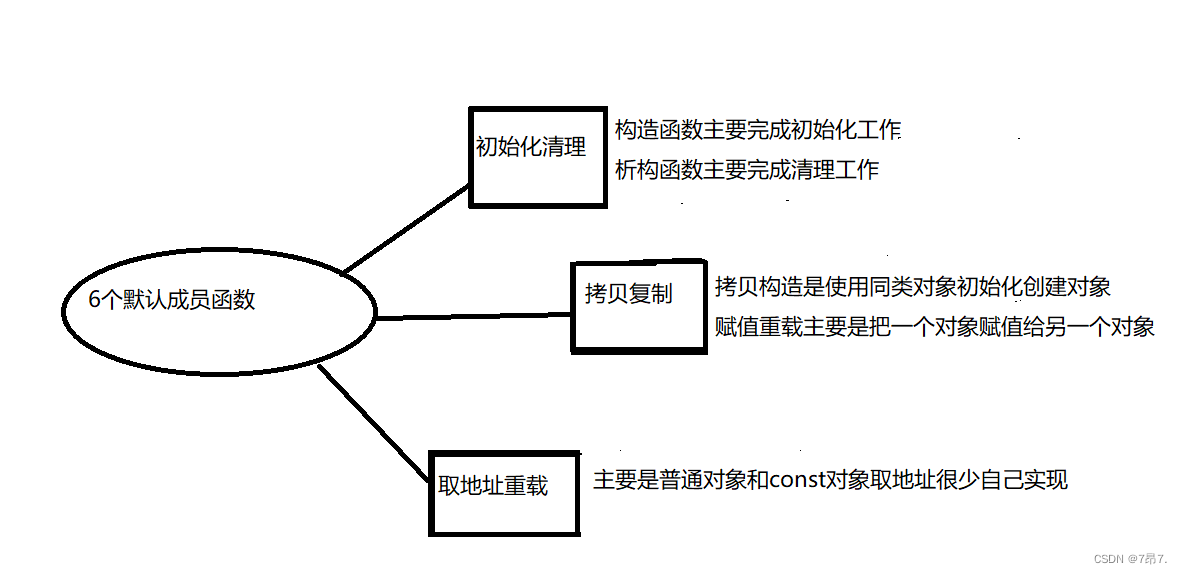
C++【类与对象】
文章目录类与对象(1)类与对象一1.0.面向过程和面向对象初步认识1.1.类的引入1.2.类的定义1.3.类的访问限定符及封装1.4.类的作用域1.5.类的实例化1.6.类的对象大小的计算1.8.类成员函数的this指针(2)类与对象二2.0类的6个默认成员…...

假设检验选择统计量重点-----正态总体参数的假设检验
文章目录单个正态总体参数的假设检验单个正态总体N(μ,σ2)N(\mu,\sigma^2)N(μ,σ2)的均值μ\muμ的假设检验1.σ2\sigma^2σ2已知(U检验法)单个正态总体方差的假设检验单边检验简介--计算拒绝域两个正态总体参数的假设检验方差已知的两正态总体均值的假设检验均值未知的两正态…...
 | 机试题算法思路 【2023】)
华为OD机试 - 通信误码(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 自动曝光(Python) | 机试题算法思路 【2023】 华为OD机试 - 双十一(Python) | 机试题算法思路 【2023】 华为OD机试 - 删除最少字符(Python) | 机试题算法思路 【2023-02】 华为OD机试 - Excel 单元格数值统计(Python) | 机试题算法思路 …...

设计模式之装饰者模式
文章の目录一、什么是装饰者模式二、优势三、缺点四、应用场景五、示例参考写在最后一、什么是装饰者模式 装饰者模式也称为包装器模式,在不改变原有对象的基础上为其动态的添加上新的功能。 装饰者模式有以下特点: 添加功能时不改变原对象结构。装饰…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...