层次分析法
目录
一:问题的引入
二:模型的建立
1.分析系统中各因素之间的关系,建立系统的递阶层次结构。
2.对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较矩阵(判断矩阵)。
3.由判断矩阵计算被比较元素对于该准则的相对权重,并进行一致性检验(检验通过权重才能用)。
4. 根据权重矩阵计算得分,并进行排序。
<1>:算数平均法求权重
<2>:几何平均法求权重
<3>:特征值法求权重
5.填充权重矩阵
6.根据权重矩阵计算得分,并进行排序
三:局限性
层次分析法(The analytic hierarchy process, 简称AHP) 建模比赛中最基础的模型之一,其主要用于解决评价类问题(例如:选择哪种方案最好、哪位运动员或者员工表现的更优秀)。
层次分析法的主要特点是通过建立递阶层次结构,把人类的判断转化到若干因素两两之间重要度的比较上,从而把难于量化的定性判断转化为可操作的重要度的比较上面。在许多情况下,决策者可以直接使用AHP进行决策,极大地提高了决策的有效性、可靠性和可行性,但其本质是一种思维方式,它把复杂问题分解成多个组成因素,又将这些因素按支配关系分别形成递阶层次结构,通过两两比较的方法确定决策方案相对重要度的总排序。整个过程体现了人类决策思维的基本特征,即分解、判断、综合,克服了其他方法回避决策者主观判断的缺点。
一:问题的引入
解决评价类问题,首先要想到以下三个问题:1 我们 评价的目标 是什么?答:为小明同学选择最佳的旅游景点。2 我们为了达到这个 目标 有哪几种可选 的方案 ?答:三种,分别是去苏杭、去北戴河和去桂林。3 评价的准则 或者说指标是什么?(我们根据什么东西来评价好坏)答:景色、花费、居住、饮食、交通。
二:模型的建立
1.分析系统中各因素之间的关系,建立系统的递阶层次结构。
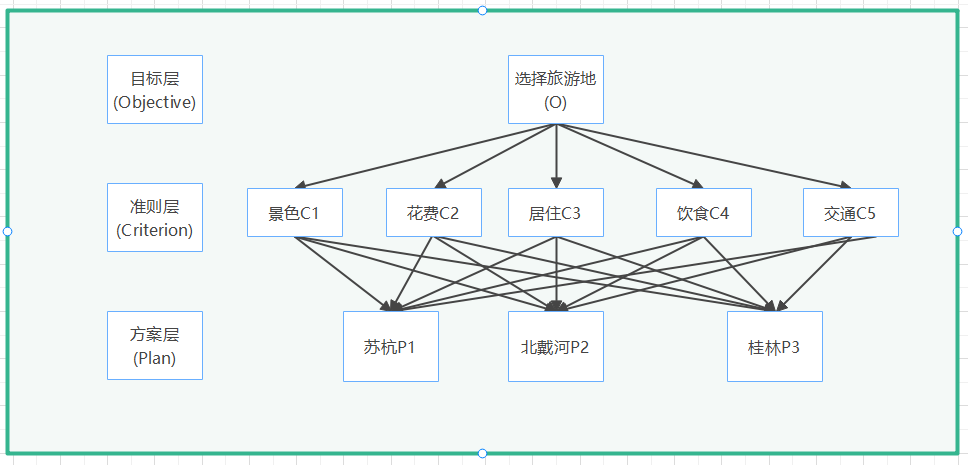
图2.1旅游地选择层次结构图
2.对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较矩阵(判断矩阵)。
层次分析法最重要使用的表格格式为:
| 指标权重 | 方案1 | 方案2 | 方案3 | ...... | |
| 指标1 | |||||
| 指标2 | |||||
| 指标3 | |||||
| ...... |
注意:同颜色的单元格的和为1,它们表示的针对某一因素所占的权重(或得分) 。
那么对应本问题,所要填写的表格如下表所示:
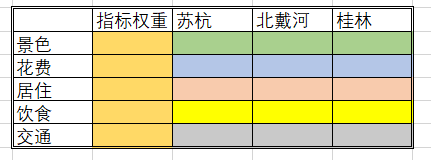
实际上,建模的最终结果就是填满权重矩阵。
| 标度 | 含义 |
|---|---|
| 1 | 表示两个因素相比,具有同样重要性 |
| 3 | 表示两个因素相比,一个因素比另一个因素稍微重要 |
| 5 | 表示两个因素相比,一个因素比另一个因素明显重要 |
| 7 | 表示两个因素相比,一个因素比另一个因素强烈重要 |
| 9 | 表示两个因素相比,一个因素比另一个因素极端重要 |
| 2、4、6、8 | 上述两相邻判断的中值 |
| 倒数 | A和 B 相比如果标度为 3 ,那么 B 和 A 相比就是 1/3 |
填写判断矩阵:
| O | 景色 | 花费 | 居住 | 饮食 | 交通 |
| 景色 | 1 | 1/2 | 4 | 3 | 3 |
| 花费 | 2 | 1 | 7 | 5 | 5 |
| 居住 | 1/4 | 1/7 | 1 | 1/2 | 1/3 |
| 饮食 | 1/3 | 1/5 | 2 | 1 | 1 |
| 交通 | 1/3 | 1/5 | 3 | 1 | 1 |
总结:上面这个表是一个 5*5 的方阵,我们记为A,对应的元素为𝑎ij .
这个方阵有如下特点:
1.aij表示的意义是,与指标𝑗相比,𝑖的重要程度。
2.当 i = 𝑗 时,两个指标相同,因此同等重要记为1,这就解释了主对角线元素为1。
如何计算苏杭、北戴河和桂林在景色、花费等方面多占的权重(得分)???
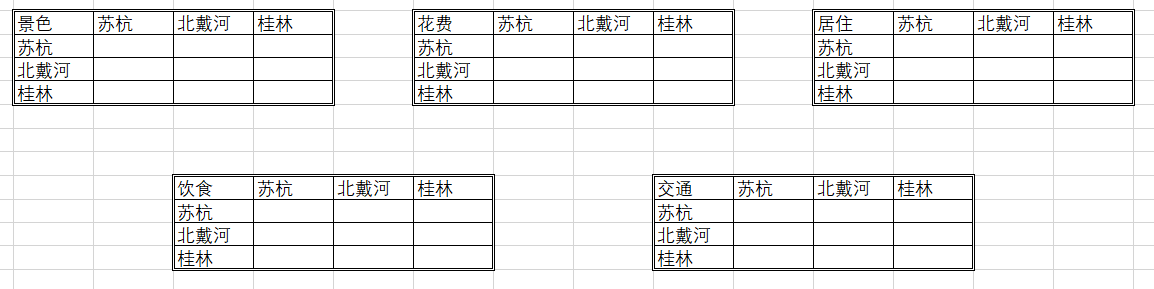
仍然使用1‐9表示重要程度,按照确定权重的方法来填写判断矩阵:
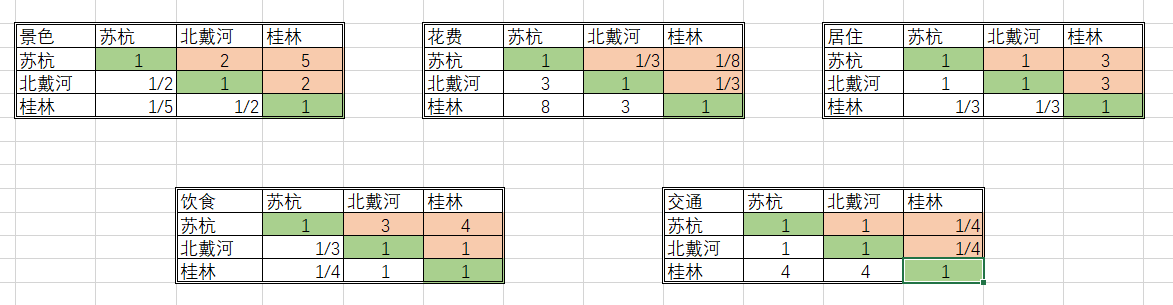
3.由判断矩阵计算被比较元素对于该准则的相对权重,并进行一致性检验(检验通过权重才能用)。
在上述五个表格中,若填写的判断矩阵为下述示例,可能会存在一个问题:
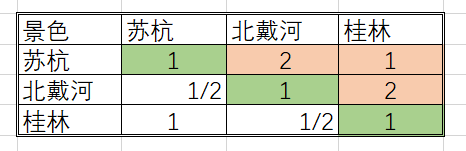
我们看景色一栏的对比,苏杭的景色比北戴河的好一点 即 苏杭 > 北戴河
苏杭的景色和桂林的景色一样好 即 苏杭 = 桂林
北戴河的景色比桂林的景色好一点 即 北戴河 > 桂林
此时,出现了矛盾的地方。

一致性检验原理:检验我们构造的判断矩阵和一致矩阵是否有太大的差别。
 若正互反矩阵(判断矩阵)满足𝑎ij * aji = aik ,则我们称其为一致矩阵。此外,n 阶正互反矩阵 A 为一致矩阵时当且仅当最大特征值 λmax = n ,且当正互反矩阵 A 非一致时,一定,满q足 λmax > n 。总而言之,判断矩阵越不一致时,最大特征值与 n 相差就越大。
若正互反矩阵(判断矩阵)满足𝑎ij * aji = aik ,则我们称其为一致矩阵。此外,n 阶正互反矩阵 A 为一致矩阵时当且仅当最大特征值 λmax = n ,且当正互反矩阵 A 非一致时,一定,满q足 λmax > n 。总而言之,判断矩阵越不一致时,最大特征值与 n 相差就越大。
一致性检验的步骤:
<1>:计算一致性指标CI
<2>:查找对应的平均随机一致性指标RI
注:在实际运用中,n很少超过10,如果指标的个数大于10,则可考虑建立二级指标体系,或使用我们以后要学习的模糊综合评价模型。 RI我们只需要会查表即可。
<3>:计算一致性比例CR。
如果CR < 0.1, 则可认为判断矩阵的一致性可以接受;否则需要对判断矩阵进行修正。
4. 根据权重矩阵计算得分,并进行排序。
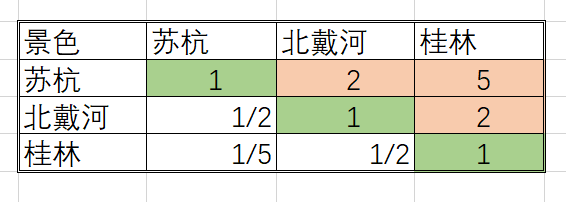
使用第一列的数据作示例,计算出来权重:
苏杭 = 1 /(1+0.5+0.2)= 0.5882
北戴河 = 0.5 /(1+0.5+0.2)= 0.2941
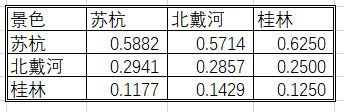
<1>:算数平均法求权重

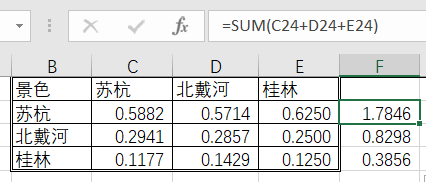
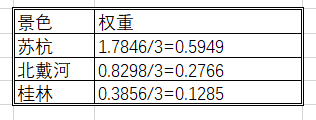
公式可写作:
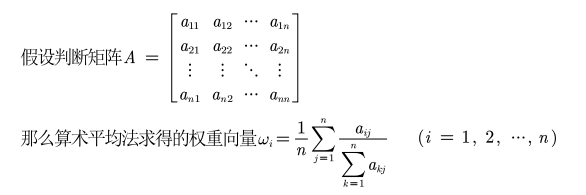
<2>:几何平均法求权重

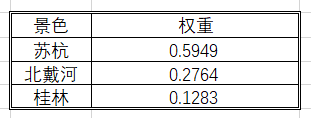
上图为几何法的计算结果。
<3>:特征值法求权重
使用二-3中求一致性检验的方法
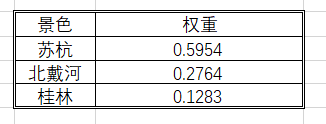
上图为特征值法的计算结果。
5.填充权重矩阵

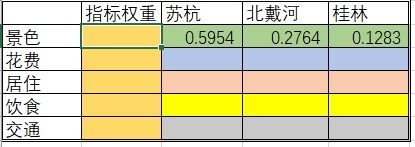
其余的矩阵按照上述的方式进行计算,得出最终的结果,在此处,不再一一计算,直接给出结果:
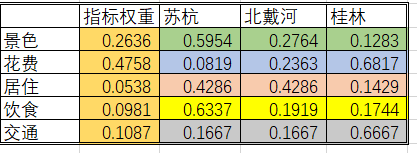
6.根据权重矩阵计算得分,并进行排序
苏杭:
0.5954×0.2636+0.0819×0.4758+0.4286×0.0538+0.6337×0.0981+0.1667×0.1087=0.299
同理:北戴河得分为0.245,桂林得分为0.455。
0.455 > 0.299 > 0.245 即 桂林 > 苏杭 > 北戴河
三:局限性

相关文章:

层次分析法
目录 一:问题的引入 二:模型的建立 1.分析系统中各因素之间的关系,建立系统的递阶层次结构。 2.对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较矩阵(判断矩阵)。 3.由判…...

Error Handling
有几个特定的异常类允许用户代码对与CAN总线相关的特定场景做出反应: Exception (Python standard library)+-- ...+-- CanError (python-can)+-- CanInterfaceNotImplementedError+-- CanInitializationError...
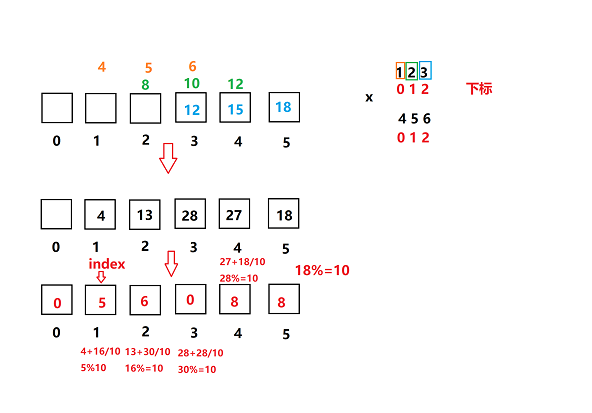
leetcode:字符串相乘(两种方法)
题目: 给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。 注意:不能使用任何内置的 BigInteger 库或直接将输入转换为整数。 示例 1: 输入: num1 "2", nu…...
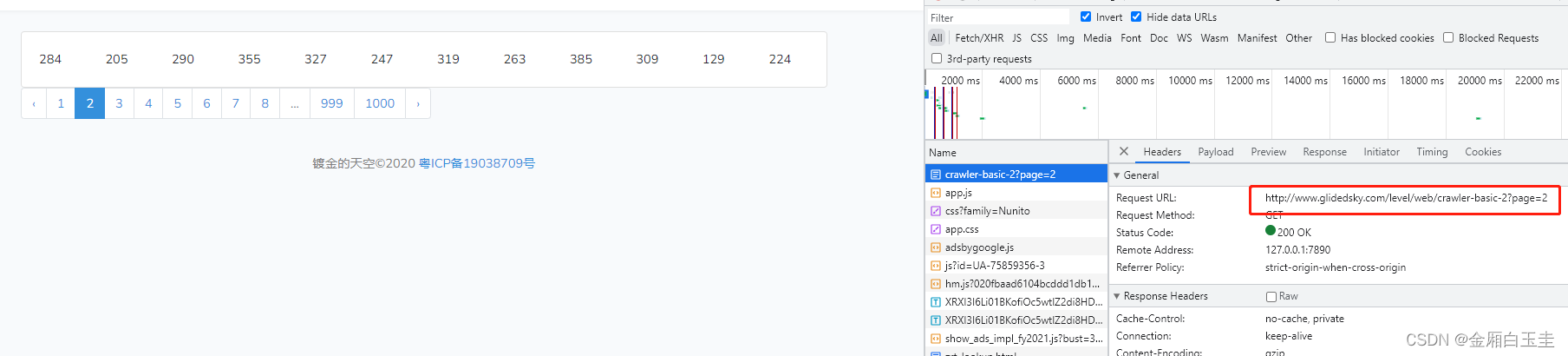
【爬虫练习之glidedsky】爬虫-基础2
题目 链接 爬虫往往不能在一个页面里面获取全部想要的数据,需要访问大量的网页才能够完成任务。 这里有一个网站,还是求所有数字的和,只是这次分了1000页。 思路 找到调用接口 可以看到后面有个参数page来控制页码 代码实现 import reques…...

03.有监督算法——决策树
1.决策树算法 决策树算法可以做分类,也可以做回归 决策树的训练与测试: 训练阶段:从给定的训练集构造出一棵树(从根节点开始选择特征,如何进行特征切分) 测试阶段:根据构造出来的树模型从上…...
网络协议详解之STP
目录 一、STP协议(生成树) 1.1 生成树协议核心知识点: 1.2 生成树协议与导致问题: 生成树含义: 1.3 802.1D 规则: 802.1D 缺点: 1.4 PVST cisco私有 1.5 PVST 1.6 快速生成树 快速的原…...
Eltima USB Network Gate 10.0 Crack
USB Network Gate -通过网络共享USB 设备 USB Network Gate (前身为以太网USB控制器USB) 轻松的通过网络(Internet/LAN/WAN)分享您的一个或者多个连接到您计算机的USB设备。 无论您身处异国还是近在隔壁办公室,您都可以轻松使用远程扫描仪、打印机、摄像头、调制解…...
)
SpringCloudGateway网关实战(一)
SpringCloudGateway网关实战(一) 目前对cloud的gateway功能还是不太熟悉,因此特意新建了对应的应用来尝试网关功能。 网关模块搭建 首先我们新建一个父模块用于添加对应的springboot依赖和cloud依赖。本模块我们的配置读取使用的是nacos&a…...
django中使用ajax发送请求
1、ajax简单介绍 浏览器向网站发送请求时 是以URL和表单的形式提交的post 或get 请求,特点是:页面刷新 除此之外,也可以基于ajax向后台发送请求(异步) 依赖jQuery 编写ajax代码 $.ajax({url: "发送的地址"…...

C++之std::list<string>::iterator迭代器应用实例(一百七十九)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

VSCode好用的插件
文章目录 前言1.Snippet Creator & easy snippet(自定义代码)2.Indent Rainbow(代码缩进)3.Chinese (Simplified) Language Pack(中文包)4.Path Intellisense(路径提示)5.Beauti…...
)
js实现滚轮滑动到底部自动加载(完整版)
这里我们用vue实现(原生js相似), 这里我们用一个div当作一个容器; <div class="JL" @scroll="onScroll" ref="inin"> <div v-for="(item,index) in this.list" :key="index" > ....…...
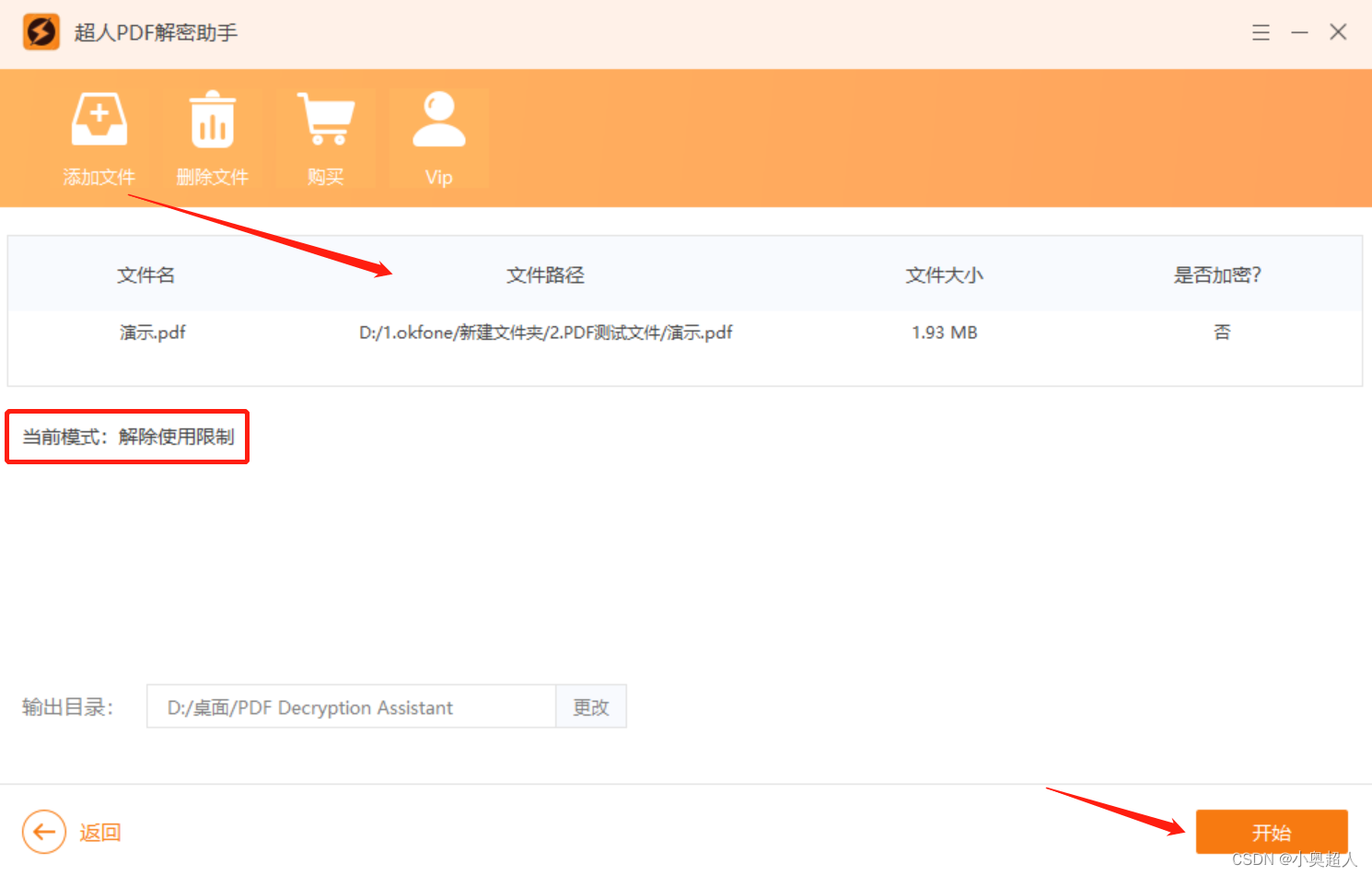
如何限制PDF打印?限制清晰度?
想要限制PDF文件的打印功能,想要限制PDF文件打印清晰度,都可以通过设置限制编辑来达到目的。 打开PDF编辑器,找到设置限制编辑的界面,切换到加密状态,然后我们就看到 有印刷许可。勾选【权限密码】输入一个PDF密码&am…...

python计算模板图像与原图像各区域的相似度
目录 1、解释说明: 2、使用示例: 3、注意事项: 1、解释说明: 在Python中,我们可以使用OpenCV库进行图像处理和计算机视觉任务。其中,模板匹配是一种常见的方法,用于在一幅图像中识别出与给定…...
阿里云云解析DNS核心概念与应用
文章目录 1.DNS解析基本概念1.1.DNS基本介绍1.2.域名的分层结构1.3.DNS解析原理1.4.DNS递归查询和迭代查询的区别1.5.DNS常用的解析记录 2.使用DNS云解析将域名与SLB公网IP进行绑定2.1.进入云解析DNS控制台2.2.添加域名解析记录2.3.验证解析是否生效 1.DNS解析基本概念 DNS官方…...
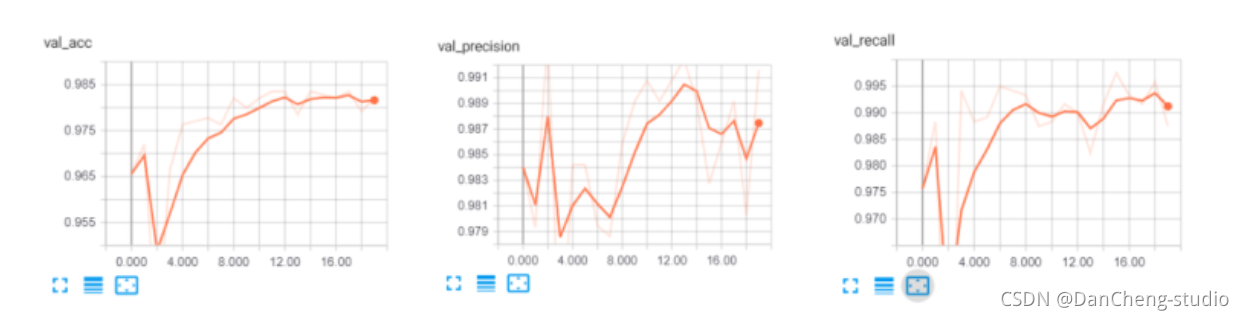
计算机竞赛 垃圾邮件(短信)分类算法实现 机器学习 深度学习
文章目录 0 前言2 垃圾短信/邮件 分类算法 原理2.1 常用的分类器 - 贝叶斯分类器 3 数据集介绍4 数据预处理5 特征提取6 训练分类器7 综合测试结果8 其他模型方法9 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 垃圾邮件(短信)分类算…...

compositionAPI
面试题:composition api相比于option api有哪些优势? 不同于reactivity api,composition api提供的函数很多是与组件深度绑定的,不能脱离组件而存在。 1. setup // component export default {setup(props, context){// 该函数在…...

vscode配置调试环境-windows系统
1. 下载Vscode 下载网址code.visualstudio.com 2. 安装vscode 直打开下载好的.exe文件进行安装即可 3.安装插件 4下载mingw编译器 4.1下载 下载网址sourceforge.net/projects/mingw-w64/files/ 下拉找到该位置,下载圈中的版本。下载速度有点慢 临时下载地址 htt…...

智慧城市能实现嘛?数字孪生又在其中扮演什么角色?
数字孪生智慧城市是将数字孪生技术与城市智能化相结合的新兴概念,旨在通过实时数字模拟城市运行,优化城市管理与服务,创造更智能、高效、可持续的城市环境。 在智慧城市中,数字孪生技术可以实时收集、分析城市各个方面的数据&…...

【置顶帖】关于博主/关于博客/博客大事记
关于博主 ● 信息安全从业者 ● 注册信息安全认证专家资质 ● CSDN认证业界专家、安全博客专家 、全栈安全领域优质创作者 ● 中国信通院【2021-GOLF IT新治理领导力论坛】演讲嘉宾 ● 安世加【2021-EISS企业信息安全峰会-上海】演讲嘉宾 ● CSDN【2022-隐私计算论坛】演讲嘉宾…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...

